Геометрические связи в задаче о движении двухколесной роликовой доски рипстик

В последние десятилетия во многих странах мира широкое развитие получили так называемые развлекательные виды спорта (англ. recreational sports). Одним из ярких примеров развлекательного вида спорта является скейтбординг — искусство катания на роликовой доске (скейтборде). Со времени появления первого скейтборда количество разных типов досок для экстремального катания достигло нескольких десятков и продолжает расти. Появились и математические модели, служащие для описания движения таких досок: известна, например, математическая модель, описывающая движение обычного скейтборда [1, 2], ряд работ посвящён динамике снейкборда [3–5].

С середины 2000-х годов популярность стал набирать двухколесный вариант скейтборда, известный как эссборд, или рипстик. Типичный рипстик, изображённый на рис. 1, состоит из двух платформ, соединённых при помощи торсионного вала, позволяющего им совершать вращения друг относительно друга. На нижней стороне каждой из платформ имеется клинообразный выступ, на наклонной грани которого закреплено рояльное колесо. Ось вращения соответствующего рояльного колеса перпендикулярна наклонной плоскости клинообразного выступа, на котором она укреплена. Этим рипстик отличается от снейк-борда, у которого колесные пары поворачиваются вокруг вертикальных осей. При катании на рипстике райдер (человек, катающийся на доске) координирует движения своих рук и тела и, наклоняя платформы, осуществляет продвижение рипстика вперёд без касания земли, одновременно сохраняя равновесие и предотвращая падение с рипстика.

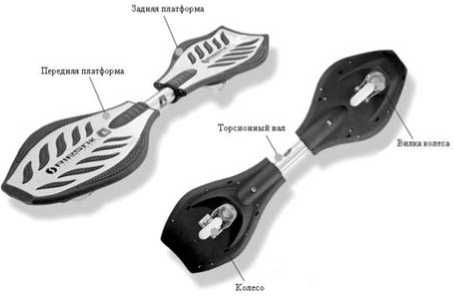
Рис. 1. Двухколесная роликовая доска рипстик: общий вид

В настоящее время остаётся не изученной не только динамическая модель рипстика, но даже и точная кинематическая модель этой системы. Лишь в работе [6] содержится описание кинематических особенностей рипстика и, в частности, получена формула, связывающая угол наклона платформы рипстика с углом поворота соответствующего колеса. При этом доказательство данной формулы опирается на сложные геометрические построения и оказывается весьма трудным для понимания. В настоящей работе предлагается другой способ получения данной формулы, использующий теорию конечных поворотов.

2.    Постановка задачи. Основное утверждение

Типичный рипстик, изображённый на рис. 1, состоит из пяти частей: переднего и заднего рояльного колеса, передней и задней платформы и торсионного вала. Торсионный вал соединяет переднюю и заднюю платформы, которые могут независимо поворачиваться относительно продольной оси рипстика.

При катании на рипстике райдер ставит свои ноги на соответствующие платформы. Под каждой платформой имеется клинообразный выступ, на наклонной плоскости которого укреплено рояльное колесо. Оси вращения l f и l _r переднего и заднего рояльного колеса перпендикулярны наклонным плоскостям соответствующих клинообразных выступов и ориентированы в противоположную сторону по отношению к направлению движения рипстика. Продольная ось рипстика E f E _r , проходящая через торсионный вал, коллинеарна продольным осям обеих платформ. Обозначим через O f и O _r точки пересечения осей вращения l f и l _r переднего и заднего рояльного колеса с наклонными плоскостями клинообразных выступов. Пусть V f и V _r — основания перпендикуляров, опущенных из точек O f и O _r на продольную ось рипстика E f E _r . Постоянный угол наклона клинообразного выступа обозначим через ε (рис. 2).

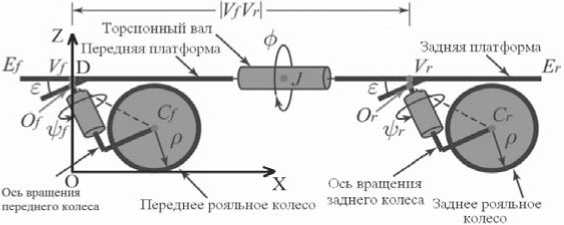
Рис. 2. Схема рипстика с обозначением основных его элементов

Обозначим через Π,Λ и Σ соответственно опорную плоскость, по которой движется рип-стик, наклонную плоскость клинообразного выступа и плоскость, проходящую через точку Of параллельно плоскости платформы. Угол наклона передней платформы (то есть угол между плоскостями Π и Σ) будем обозначать δf . Значениям δf > 0 (δf < 0) соответствует наклон передней платформы влево (вправо), если смотреть в направлении движения рип-стика. Угол наклона задней платформы будем обозначать δr . Предположим, что рипстик движется по плоскости Π таким образом, что его продольная ось EfEr остаётся параллельной плоскости Π во всё время движения. Это возможно, если во всё время движения углы δf и δr связаны соотношением

5 f = i5 _r .                                            (1)

Обозначим через O f ( O , ) основание перпендикуляра, опущенного из точки O f ( O r ) на плоскость Π. Основание перпендикуляра, опущенного из точки V f ( V _r ) на ту же плоскость П обозначим V ' ( V'. ). Поскольку мы предполагаем, что во всё время движения продольная ось рипстика E f E _r остаётся параллельной плоскости Π, то, следовательно,

V f V r I I V f V ' и |V f V| = | V f V '\.                            (2)

В силу конструктивных особенностей рипстика, если его платформы не наклонены, то колёса лежат в вертикальной плоскости, перпендикулярной плоскостям платформ и опорной плоскости Π. При наклоне платформы плоскость колеса, оставаясь перпендикулярной плоскости Π, поворачивается таким образом, что она будет перпендикулярна линии пересечения плоскостей Π и Λ. При этом продольная ось рипстика образует с плоскостью колеса некоторый ненулевой угол. Поскольку отрезок V f V _r является частью продольной оси E f E _r и справедливы условия (1), (2), то будем определять угол поворота колеса как угол между прямой V f V ' и плоскостью колеса. Будем обозначать этот угол через T f . Тогда справедливо следующее утверждение, впервые доказанное в работе [6].

Теорема 1. Угол наклона платформы δf и угол поворота колеса τf связаны соотношением sin δf =tgε tg τf .                                     (3)

При доказательстве формулы (3) в работе [6] использовались сложные геометрические построения, сильно затрудняющие понимание. Мы предлагаем здесь более простой вариант доказательства, основанный на теории конечных поворотов.

Рассмотрим переднюю платформу рипстика в положении, когда она не наклонена. Введём систему координат OXY Z таким образом, что точка O — начало данной системы координат — принадлежит плоскости Π, ось OZ перпендикулярна плоскости Π и проходит через точку Of , а ось OX направлена параллельно продольной оси рипстика Ef Er . Единичные векторы введенной системы координат будем обозначать ex , ey, ez (рис. 2). Пусть плоскость платформы рипстика расположена на высоте h над плоскостью Π. Точку пересечения продольной оси рипстика Ef Er с плоскостью Λ обозначим через D. Пусть расстояние DOf = a. Тогда относительно введённой системы координат плоскость Π определяется уравнением Z = 0, а плоскость X определяется уравнением Z = h — a sin е. Относительно введённой системы координат вектор нормали к плоскости Λ имеет вид n = — sin еex + cos еez,                                  (4)

а сама плоскость Λ проходит через точку Of , радиус-вектор которой имеет вид rOf = (h — a sin е) ez.                                     (5)

Поэтому уравнение плоскости Λ записывается следующим образом:

• — sin eX + cos eZ = cos е ( h — a sin е ) .

Плоскости Π и Λ пересекаются по прямой, определяемой уравнениями

X = — cos e ( h — a sin е ) , _z = _Q .

sin ε

Данная прямая будет перпендикулярна вертикальной плоскости Y =0— плоскости, в которой располагается колесо. В силу конструктивных особенностей рипстика, при наклоне платформы плоскость колеса, оставаясь перпендикулярной плоскости Π, поворачивается таким образом, что она будет перпендикулярна линии пересечения плоскостей Π и Λ. При этом вертикальная плоскость, содержащая продольную ось рипстика, образует с плоскостью колеса некоторый ненулевой угол. Именно этот угол и будем считать углом поворота колеса τf . Выразим его через угол наклона платформы δf .

Как известно из теории конечных поворотов (см., например, [7]), если некоторыйвектор ρ повернуть на угол χ вокруг оси с единичным направляющим вектором e , то в результате поворота вектор р перейдёт в вектор р такой, что

р = (е • Р) e + (Р - (е • Р) е) cos X + [е х р] sin х, где (е • р) обозначает скалярное, а [е х р] - векторное произведение векторов е и р.

Предположим, что передняя платформа рипстика наклонилась вправо по отношению к направлению движения рипстика таким образом, что угол между плоскостью платформы и опорной плоскостью стал равным δ f . Это равносильно тому, что передняя платформа повернулась на угол 5 f вокруг оси с направляющим вектором е = — е x . Тогда по формуле (6) вектор нормали n к плоскости Λ, определяемый формулой (4), перейдёт в вектор

• n * = — sin ее x + cos e sin 5 f е y + cos e cos 5 f е z .

  
  

Аналогично, радиус-вектор точки Of , до наклона платформы определявшийся формулой (5), примет вид rOf = (h — a sin e) sin 5f еy + (h — a sin e) cos 5f еz.

Таким образом, после наклона платформы плоскость Λ занимает такое положение, при котором вектором нормали к ней является вектор n * , определяемый формулой (7), а точка O f с радиус-вектором r O f принадлежит этой плоскости. Отсюда получаем уравнение плоскости Λ после наклона платформы:

—

^{sin ε}X +sin δ f Y +cos δ f Z = h cos ε

— a sin e.

Эта плоскость пересекается с плоскостью Π по прямой:

— sin ^e X + sin 5 _f Y = h — cos ε

a sin ε.

Направляющим вектором прямой (8) является вектор cos ε sin ε x

e y . sin δ f

Уравнение плоскости, перпендикулярной вектору s и проходящей через текущее положение точки Of, имеет вид coseX +-- ү = h — a sin e.

sin ε      sin δ f

В силу упоминавшихся выше конструктивных особенностей рипстика именно в этой плоскости будет лежать колесо после наклона платформы. Поэтому угол поворота колеса τf определяется в данном случае как угол между плоскостью Y =0и плоскостью, заданной формулой (9). Пользуясь стандартными формулами для угла между плоскостями, находим cos ε sin δf , sin ε откуда следует формула (3).

Заметим, что условия (1) и (2) играют существенную роль в проведённых рассуждениях. Если углы наклона платформ рипстика не связаны соотношением (1), то его продольная ось не будет параллельна плоскости Π, а будет образовывать с ней некоторый ненулевой угол ν , причём соотношения, связывающие углы наклона платформ с углами поворота колёс, будут сложным образом зависеть от ν . В дальнейшем мы собираемся рассмотреть этот случай и представить самые общие зависимости между углами наклона платформ рипстика и углами поворота его колёс.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, проекты № 16-01-00338 и № 17-01-00123.