Геометрические свойства пространства вероятностных мер являющихся бесконечномерными многообразиями

v                                                      Р (X I

Пусть бесконечный метрический компакт. Пространство вероятностных мер, которое состоит из всех непрерывных,

неотрицательных и нормированных линейных функционалов т.е. ={ ^■.CVXOR^ - непрерывный, линейный, неотрицательный нормированный X        D _                          _ С(^] = {/ ;Х^Р } функционал, - множество действительных чисел}, где рассматривается компактно-открытая

непрерывно. На множестве топология.

базу топологий составляют следующего вида

На пространстве открытые множества:

О(А=^ = ^= -=^=^ )=

Определение 1[1-4]. Хаусдорфово топологическое пространство называется - многообразием, моделированным на пространстве - или многообразием, если всякая точка пространства имеет открытую окрестность, гомеоморфную открытому подмножеству пространства -

ГТ па                                  И Е .V                    )

Для натурального числа        , через         обозначим вероятностные меры, ■“ носители которых содержат не более чем я точек т.е. Рг (А") = ^ Е Р( А'):|supp(// )| < н}

2- П. ^Ч:              Г-! П

:--        - гильбертов куб, - отрезок в

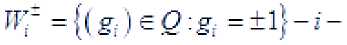
ая грань куба ;

BdO = :-:    псевдограница куба ;

о вао=з _                  О

- псевдовнутренность куба

Теорема 1. Для любого бесконечного компакта и любого ?Т Е Л , подпространство                  пространства           является - многообразием.

Из этой теоремы из определений - многообразий.

Следствие 1. Для любого бесконечного компакта и любого его всюду плотного подмножества подпространство является многообразием. Через

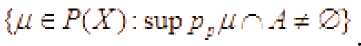
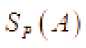
обозначается

множество

Теорема 2. Для любого бесконечного метрического компакта и любого открытого               подпространство         является - многообразием.

Следствие 2. Для любого бесконечного метрического компакта и

J = X                   ^Л )    5

подмножества , подпространство         есть - многообразие.