Геометрический критерий потери несущей способности сталежелезобетонных стержней

Большинство процессов, происходящих в природе и технике, носят необратимый характер, при этом имеют достаточно строгое и точное аналитическое описание. Именно поэтому могут быть построены математические модели, позволяющие не только оценить текущее состояние инженерной системы или конструкции, но также спрогнозировать ее поведение при определенном развитии и изменении внешних факторов (температурного режима, силовых воздействий и т. д.).

Для разработки математических моделей необходимо проведение экспериментальных исследований с получением точных данных, а также геометрическое описание изученных процессов и построение кривых, описывающих те или иные явления. Однако помимо кривых и поверхностей, описывающих данные явления, необходима разработка геометрических критериев, являющихся индикатором наступления того или иного характерного или критического состояния. В частности, при описании кривых деформирования важной задачей является разработка геометрического критерия, фиксирующего потерю прочности или несущей способности того или иного материала или инженерной конструкции.

Разработка математических моделей и геометрическое описание процессов деформирования применяется при создании систем автоматизированного проектирования и расчета (САПР), поскольку результат исследования может быть заложен в алгоритм работы программно-вычислительных комплексов с целью использования аналитических соотношений для численного решения задач по определению напряженно-деформированного состояния конструкций. Таким образом, создание геометрических моделей необходимо при всем информационном сопровождении жизненного цикла изделий и конструкций [1].

Современная наука и техника нашли новаторский подход в использовании конструкционных материалов, объединяя их в уникальные сочетания. Так, трубобетон – это одно из передовых решений, где стальная труба заполняется бетоном, образуя композитную конструкцию. Такая инновация позволяет объединить лучшие качества стальных и железобетонных элеметов, минимизируя из недостатки и повышая эффективность.

Сталежелезобетонные конструкции в последние годы находят широкое применение в строительстве [1–4], в связи с чем обретают повышенный интерес как отечественных [3–9], так и зарубежных [10–14] ученых. Активно проводятся экспериментальные [6, 10–13], численные [4] и аналитические [3, 5–8, 14–16] исследования, однако существующая нормативная документация [17] до сих пор имеет достаточное количество неосвещенных вопросов, а расчетные методики не позволяют точно описать напряженно-деформированное состояние трубобетонных элементов.

Предметом настоящего исследования являются лабораторные образцы коротких сталебетонных стержней, испытываемые кратковременной сжимающей нагрузкой с целью дальнейшего аналитического описания их процесса деформирования и разработки геометрического критерия потери несущей способности.

Метод

Для построения математических моделей деформирования, используемых при разработке геометрического критерия потери несущей способности сталебетонных стержней малогабаритных сечений, были подготовлены лабораторные образцы, состоящие из прямошовных электросварных стальных труб, заполненных бетонным сердечником (рис. 1). Дополнительное армирование сердечника гибкой стержневой арматурой не применялось ввиду стесненности поперечных сечений. Для равномерной передачи нагрузки торцы стальных труб были фрезерованы, заполнялись высокоподвижной бетонной смесью с избытком и последующей торцовкой при помощи алмазного диска. Помимо сталебетонных стержней для каждого типоразмера также были изготовлены полые образцы стальных труб.

Для проведения испытаний образцов длиной 100 мм использовалась экспериментальная установка (рис. 2), оснащенная прессом П-125, при помощи которой подавалась осевая сжимающая нагрузка на установленные между загружающими пластинами стержни. Нагрузка прикладывалась плавно и считается кратковременной, в связи с чем не учитывается явление ползучести. На протяжении всего периода нагружения образцов при помощи индикатора часового типа фиксировалось

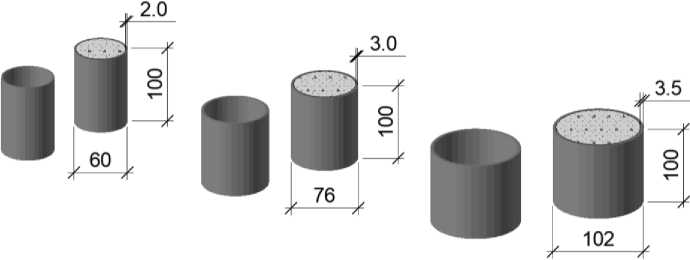
а)                               б)                                 в)

Рис. 1. Лабораторные образцы стальных и сталебетонных стержней для экспериментального исследования: внешний диаметр трубы D = 60 мм и толщина стенки t ст = 2,0 мм (а), D = 76 мм и t ст = 3,0 мм (б), D = 102 мм и t ст = 3,5 мм (в)

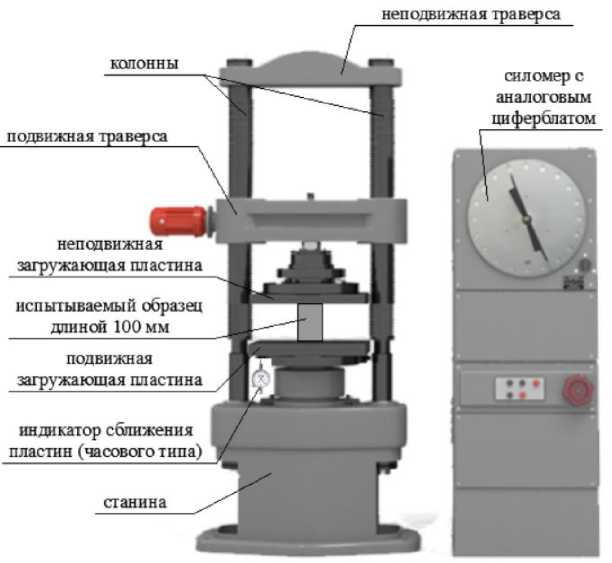
неподвижная траверса неподвижная загружающая пластина испытываемый образец длиной 100 мм станина колонны подвижная траверса силомер с аналоговым циферблатом подвижная загружающая пластина индикатор сближения I пластин (часового типа)

Рис. 2. Схема экспериментальной установки для испытаний стальных и сталебетонных стержней осевой сжимающей нагрузкой в испытательном прессе П-125 [18]

сближение пластин пресса, соответствующее полной продольной деформации стержня при сжатии.

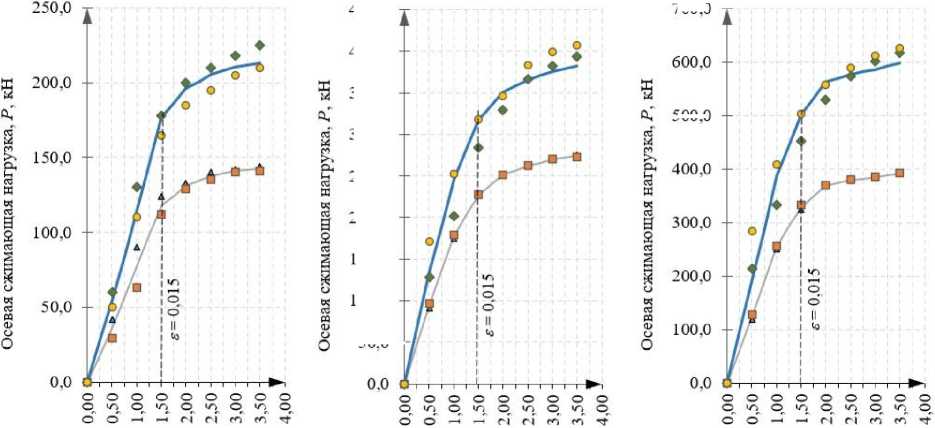
Результаты экспериментальных исследований были обработаны и представлены в виде диаграмм продольного деформирования (рис. 3). Помимо исследуемых диаграмм для сталебетонных стержней также строились графики для полой стальной трубы. Прослеживается очевидная зависимость между графиками - диаграмма для стержней с бетонным сердечником подобна диаграмме для полой трубы с соответствующими размерами. Кроме того, область упругих деформаций для стальных и сталебетонных образцов имеет одни и те же пределы. Таким образом, наличие в трубе сердечника вносит определенный вклад в несущую способность конструкции, причем этот вклад постоянный на каждом этапе деформирования, чем вызвано подобие изучаемых диаграмм. На предположении о соизмеримости вклада бетона на всех этапах нагружения также основана методика, предложенная в [19].

В статье [20] предлагается инженерная модель деформирования, при помощи которой может быть вычислено значение осевой сжимающей силы P при произвольном значении продольной деформации А:

P_tb(^) = P_t(Ar (1 + 2,5 ^), (1)

700,0

450,0

400,0

350,0

300,0

250,0

200,0

150,0

100,0

500.0

50.0 +

Неупругие деформации

Неупругие деформации

Упругие деформации

Неупругие деформации

Упругие деформации

Упругие деформации

Продольные деформации, А, мм

Продольные деформации. А, мм

Продольные деформации, А, мм

* □    - результаты экспериментальных исследований для стальной трубы

• ♦ о   - результаты экспериментальных исследований для сталебетонных стержней

• ■ осредненная диграмма деформирования для стальной трубы, полученная по экспериментальным данным

  ---   - диаграмма деформирования сталебетонного стержня, построенная по инженерной модели

Рис. 3. Диаграммы продольного деформирования стальных и сталебетонных образцов при сжатии осевой нагрузкой, полученные экспериментально и при помощи инженерной модели: труба 60 х 2,0 (а), труба 76 х 3,0 (б), труба 102 х 3,5 (в)

где P_tb (Д) и P_t (Д) - продольная сила в сталебетонном стержне и стальной трубе, соответствующая продольному перемещению торцов Д;

P_b^r и Р ^ - предельная несущая способность стальной трубы (обоймы) и бетонного сердечника при их раздельной работе, которые могут быть определены по существующим нормативным методикам для проектирования.

Предложенная формула удобна, поскольку позволяет оценить порядок деформаций и скорость деформирования сжатых сталебетонных стержней малой гибкости и подходит для расчета элементов с различными размерами сечений. Однако данная методика не является универсальной, которая могла бы аналитически описать деформирование трубобетона для последующего внедрения в САПР, поскольку для получения искомого графика P_tb (Д) необходимо сначала построить график для стальной трубы P_t (Д).

Результаты и обсуждения

В ходе анализа полученных диаграмм были подобраны аналитические функции, позволяющие описать процесс деформирования сталебетонных элементов при помощи математического моделирования. При этом диаграмма представлена в виде непрерывной кусочно-заданной функции (рис. 4):

линейной AB на участке с относительными деформациями 0 < е < 0,01 (упругий участок деформирования) и логарифмической BC при больших деформациях (е > 0,01):

^(Д) = Pt(Д)• (1 + 2,5 •P^),      (2)

где Д - осевое укорочение образца (смещение торцов), мм;

А - постоянная для конструкции, зависящая от геометрических характеристик сечений и применяемых материалов:

А = k_m-P_t^cr-(1 + к_ь^)       (3)

к_т = 0,85 - коэффициент масштабирования модели;

к_ь = 2,5 - коэффициент, учитывающий вклад бетона в работу конструкции;

к_Д = 5 - коэффициент масштабирования перемещений.

Логарифмическая функция BC подобрана так, чтобы она соответствовала действительному процессу деформирования, полученного путем построения и обработки диаграмм по экспериментальным данным. Линейная функция (прямая AB ) определяется из условия, что прямая проходит через начало координат (точка 0;0) и что линейная функция должна непрерывно переходить в логарифмическую (общая точка B ).

700,0 т

450,0 j-

Условное

Условное

400,0 -

Условное разрушение

разрушение разрушение

Продольные деформации. Л, мм

Продольные деформации, Д, мм

Упругие деформации

Упругие деформации

Неупругие деформации

Неупругие деформации

Упругие деформации

Неупругие деформации

Продольные деформации, Д, мм б)

□

• -    результаты экспериментальных исследований для стальной трубы

  ♦ о

  
  

• -    результаты экспериментальных исследований для сталебетонных стержней

• -    осредненная диграмма деформирования для стальной трубы, полученная по экспериментальным данным

• -    диаграмма деформирования сталебетонного стержня, построенная по математической модели

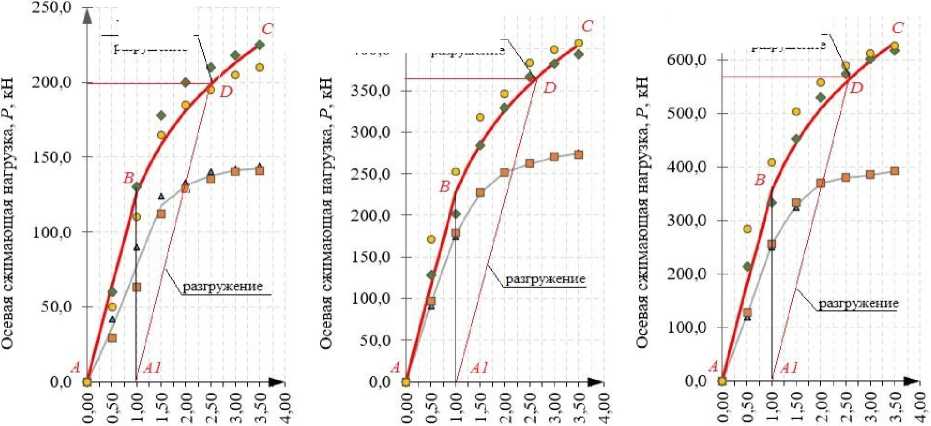
Рис. 4. Диаграммы продольного деформирования стальных и сталебетонных образцов при сжатии осевой нагрузкой, полученные экспериментально и при помощи математической модели в виде кусочно-заданной функции: труба 60 х 2,0 (а), труба 76 х 3,0 (б), труба 102 х 3,5 (в)

Традиционно для материалов, диаграммы деформирования которых не имеют явно выраженной площадки текучести, за условный предел текучести принимается значение напряжения σ у , при котором остаточная относительная деформация образца достигает некоторого критического значения 8 _ост cr [21].

Поскольку сталебетонный стержень имеет неоднородное поперечное сечение, состоящее из материалов с различными прочностными и деформационными характеристиками, то в этом случае необходимо говорить не о классической диаграмме деформирования в напряжениях и относительных деформациях с - е, а о зависимости между продольной сжимающей силой и абсолютным укорочением исследуемого образца P -Л.

Диаграммы деформирования [18] показывают, что при лабораторных испытаниях сжимающей нагрузкой деформации неограниченно возрастают, не вызывая явного разрушения образца. Возникает необходимость введения однозначного критерия потери несущей способности, т. е. сжимающей силы, при которой невозможна дальнейшая эксплуатация конструкции.

На графике кусочно-заданной функции точка B является граничным значением между линейным и логарифмическим участками. За момент услов- ного разрушения сталебетонного стержня предлагается принять продольную силу, соответствующую пересечению логарифмической кривой BC и «линии разгружения» A 1 D, которая параллельна начальному этапу деформирования AB и соответствует критическому значению остаточных деформаций еост cr = 0,01.

[ P_t b (b) = ШДДД-Д ост ^сг)

I    P_a(k) = Ш^Д).

Приравнивая правые части приведенных функций, получаем уравнение, являющееся критерием потери несущей способности:

1д(к_й)^(Д^сг-Д ост ^сг) = 1д(к_й^, (5) где Д _ост ^сг = е _ост ^сг • L₀ - критическое абсолютное значение остаточных осевых деформаций образца при его разгружении, мм;

• L ₀ - первоначальная длина образца, мм.

Приведенное выше уравнение не имеет аналитического решения, однако графики исследуемых функций (см. рис. 4) указывают на то, что уравнение однозначно имеет единственное решение, которое можно получить численным или графоаналитическим методами. Решением уравнения является критическая деформация Д^сг , по которой может быть определена критическая сила, соот-

Значения критических осевых деформаций и условного предела несущей способности сталебетонных образцов, полученные численным решением

Типоразмер трубы-обоймы △остсг, мм С   СГ ^ост Ptbcr, кН Ptcr, кН РЬСГ, кН Ptbc ---—100% р cr   р cr      /и 60x2.0 2,59 0,0259 201,3 142 28,2 118 % 76x3.0 2,59 0,0259 362,4 275 43,5 114 % 102x3.5 2,59 0,0259 564,9 392 82,3 119 % ветствующая условной потере несущей способности Ptbcr, по формуле

Р^ = A-lg^-l^. (6)

Численное решение системы уравнений для каждого из трех типоразмеров образцов приведено в таблице.

Выводы

По результатам проведенных экспериментальных исследований и их аналитической обработки были сделаны следующие выводы:

• 1.    Деформирование сталебетонных стержней малой гибкости происходит аналогично деформированию стальной трубы, при этом вклад бетонного сердечника в общую несущую способность постоянный в течение всего процесса нагружения. И для полых образцов, и для образцов с сердечником область упругих деформаций находится в одинаковых пределах.

• 2.    Предложена кусочно-заданная функция, позволяющая описать процесс деформирования методами математического моделирования. При малых деформациях при 0 < £ < 0,01 образцы деформируются упруго по линейному закону. При £ > 0,01 имеют место пластические деформации, увеличивается скорость деформаций, что соответствует логарифмической зависимости P – ∆.

• 3.    Разработан геометрический критерий потери несущей способности при монотонно возрастающей кривой деформирования, позволяющий определить значение критической продольной сжимающей силы, при которой остаточные деформации превышают допускаемые значения. Предложенный критерий однозначно определяет значение сжимающей силы, при которой невозможна дальнейшая эксплуатация конструкции.