Геометрическое и конечно-элементное моделирование сетчатой конической оболочки с геодезической траекторией спиральных ребер

Введение. Сетчатые оболочки различной конфигурации, изготавливаемые из композиционных материалов, получили широкое распространение в различных отраслях машиностроения [1]. В частности, в космической отрасли в качестве частей ступеней ракет-носителей, силовых конструкций космических аппаратов и адаптеров полезной нагрузки, служащих для связи космического аппарата со средствами выведения, применяются цилиндрические и конические сетчатые оболочки [2-4].

Конические оболочки, в настоящее время применяемые в АО «ИСС», проектируются и изготавливаются методом автоматической намотки с траекториями спиральных ребер, ориентированными вдоль геодезических линий, представляющих собой прямые линии на развертке поверхности конуса [5; 11].

Известно, что в сетчатой конической оболочке с траекторией спиральных ребер в виде локсодромы (кривой на поверхности вращения с одинаковыми углами относительно образующей) уровень максимальных напряжений, например, от действия боковой силы увеличен (относительно конструкции со спиральными ребрами, расположенными по геодезическим линиям) на 38 % [6]. Поэтому при проектировании конструкций на основе сетчатых конических оболочек немаловажным является точное моделирование, отражающее действительное положение спиральных ребер [7-10].

Особенности конечно-элементного моделирования сетчатых конических оболочек. В настоящее время для оценки прочности и жесткости различных конструкций широко применяется метод конечных элементов [12; 13]. Одним из способов создания конечно-элементной модели (КЭМ) является разбиение уже имеющейся геометрической модели на конечные элементы. Создаваемые геометрические модели конструкции для последующего разбиения на конечные элементы имеют некоторые особенности в отличие от геометрических моделей, создаваемых для разработки конструкторской документации:

• -    если конструкция симметрична, достаточно смоделировать повторяющийся элемент;

• -    в модели не должно быть совпадающих точек, линий, поверхностей, их наличие может затруднить разбиение геометрии на конечные элементы;

• -    конец каждого отрезка должен совпадать с началом следующего, т. е. не должно быть разрывов и пересечений линий.

С учетом описанных особенностей создана геометрическая модель сетчатой конической оболочки с геодезической траекторией спиральных ребер (рис. 1) для последующего создания её конечно-элементной модели.

Для построения КЭМ сетчатой конической оболочки достаточно создать геометрическую модель одного сегмента и сгенерированные на основе этой геометрии конечные элементы скопировать по окружности вокруг продольной оси оболочки [14]. Элементарный сегмент сетчатой конической оболочки приведен на рис. 2.

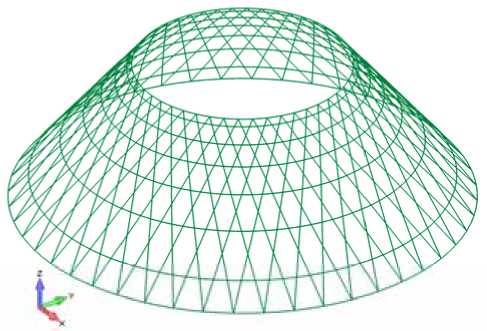
Рис. 1. Геометрическая модель сетчатой конической оболочки с геодезической траекторией спиральных ребер

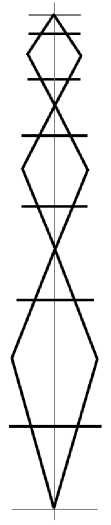
Рис. 2. Элементарный сегмент сетчатой конической оболочки

Геометрическое моделирование. На рис. 2 видно, что элементарный сегмент сетчатой конической оболочки представляет собой набор отрезков, соединенных между собой определенным образом. Задача о построении геометрической модели сегмента сетчатой конической оболочки сводится к определению координат точек начала и конца каждого отрезка сегмента в заданной системе координат в зависимости от основных проектных параметров сетчатой конической оболочки.

Как известно, основными проектными параметрами для сетчатой конической оболочки являются:

• -    h - высота конуса;

• -    r - радиус основания конуса;

• -    у — угол наклона образующей конуса;

• -    n - количество однозаходных спиральных ребер;

• -    5 - угол выхода спирального ребра.

Для определения координат точек начала и конца отрезков, из которых состоит сегмент сетчатой конической оболочки, введем понятие «пояс точек пересечения ребер» - точки пересечения ребер, лежащие в одной горизонтальной плоскости (рис. 3), и переменную i , обозначающую порядковый номер пояса.

PCi) =

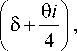
®(i) = 1 90° +6 I.

I 8 J

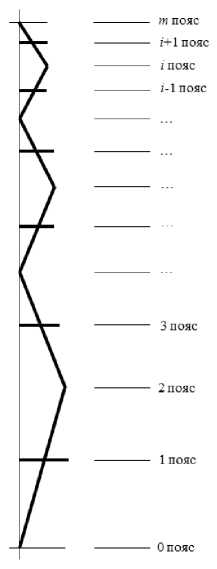
Рис. 3. Пояса точек пересечения ребер

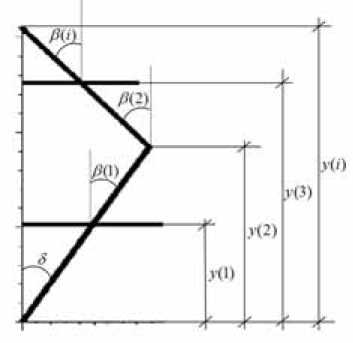
Рис. 4. Координата у поясов точек элементарного сегмента

Для определения количества поясов точек i в зависимости от высоты адаптера используется уравнение Клеро [15]:

r sin( 5 ) = r ( i ) sin( P ( i )),                  (7)

где r ( i ) - радиус i -го пояса.

Подставим выражение (5) в уравнение (7), а радиус i -го пояса запишем в следующем виде:

h r (i) = r-- tg(y)

Уравнение (7) примет вид

r sin( 5 ) =

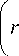
h tg⁽ Y ⁾

Выражая i , получим:

.

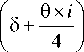
Г r sin( 5 )tg( y )

- 5 + arcsin |

( ^r tg⁽ y ^{) -} h

i = 4----------------------------6

.

Таким образом, координаты точек начала и конца отрезков напрямую зависят от того, в каком поясе точек пересечения ребер они находятся.

Координата у i -го пояса точек (рис. 4) определяется по следующей формуле:

У ⁽ i ) = a ⁽ i ⁾sin⁽ y ^{),                    (1)}

где величины, определяемые по развертке сетчатой конической оболочки (рис. 5), равны:

a ( i ) = b ⁽ i ⁾sin⁽ P ⁽ i ) + ю ⁽ i )) sin( P ( i ))

2r Г Л 6i)) b(i) =            I sin | II,

cos(y) (   ( 8 JJ

360 ° cos( y )

6 =------------,

n

Подставив в уравнение (8) конкретные значения, мы получим нецелое число i . Этот факт вполне объясним, он говорит о том, что при моделировании реальной конструкции с заданными проектными параметрами координата у последнего пояса и высота адаптера могут не совпадать. Для практического применения значение i , полученное по формуле, необходимо округлить до ближайшего целого числа.

Вычисленная координата у позволяет достаточно просто определить координаты x и z каждой характерной точки элементарного сегмента сетчатой конической оболочки.

Заключение. На основании изложенного выше был разработан алгоритм автоматического расчета координат начала и конца отрезков элементарного сегмента сетчатой конической оболочки с геодезической траекторией спиральных ребер в зависимости от проектных параметров конической оболочки.

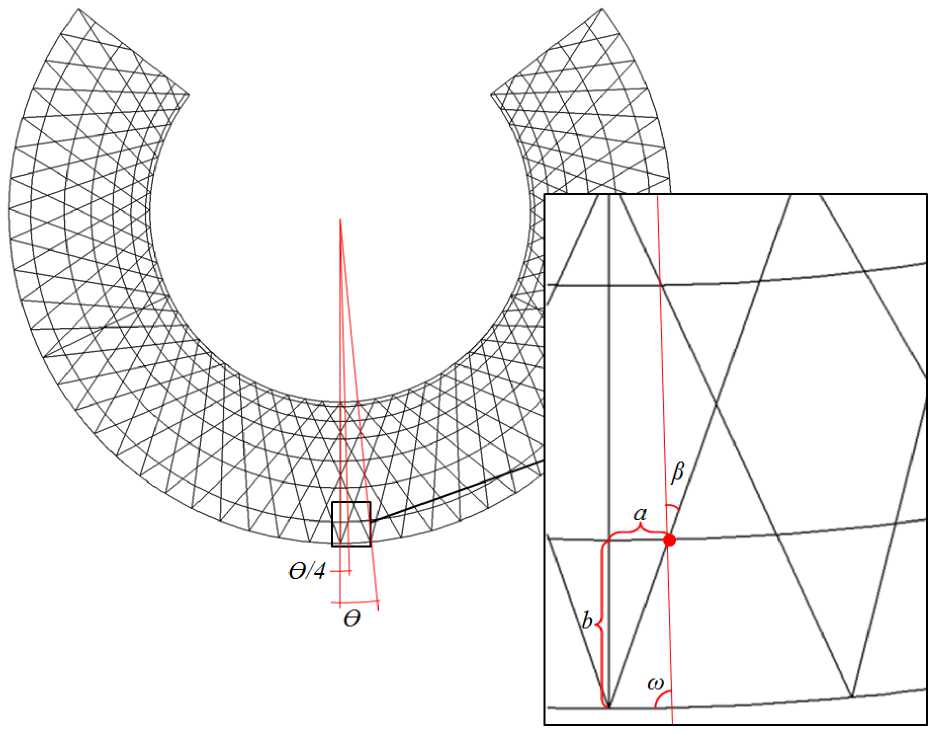
Рис. 5. Развертка сетчатой конической оболочки

Рис. 6. Этапы построения конечно-элементной модели элементарного сегмента в среде Femap with NX Nastran

Реализация данного алгоритма на встроенном языке программирования любой САПР позволяет в автоматическом режиме строить геометрическую модель элементарного сегмента сетчатой конической оболочки для ее последующего разбиения на конечные элементы. Это значительно упрощает и ускоряет процесс анализа сетчатых конических оболочек программны ми средствами. На рис. 6 приведены этапы построения конечно-элементной модели элементарного сегмента конической оболочки с использованием описанного алгоритма в среде Femap with NX Nastran.

Acknowledgments. This work was supported by the Ministry of Education and Science of the Russian Federation, unique identifier of the project RFMEF157414X0082.