Геометрическое конструирование оболочек способом выхода в четырехмерное пространство

В практике архитектурного проектирования накоплен большой опыт использования алгебраических поверхностей [1]. Дополнительные возможности появляются в связи с развитием средств компьютерной графики.

С инженерной точки зрения большое практическое значение имеют геометрические алгоритмы построения поверхности, натягиваемой на данный криволинейный контур.

Постановка задачи. Разработать конструктивный графический алгоритм закономерного построения поверхности на четырехзвенном контуре, образованном плоскими кривыми линиями.

Очевидно, в трехмерном пространстве E³(xyz) задачу приходится считать неопределенной, поскольку через данный контур (рис. 1) может проходить множество различных поверхностей.

Неопределенность можно устранить, если «погрузить» контур в четырехмерное пространство E⁴(xyzt) , придав узлам A , B , C , D произвольные координаты по оси t [2, 3]. При этом исходный контур ABCD становится ортогональной проекцией на гиперплоскость xyz некоторого замкнутого контура w , размещенного в четырехмерном пространстве xyzt . Соответственно изменяется и формулировка задачи.

Составить алгоритм построения точек и линий на двумерной поверхности, проходящей через замкнутый контур w, расположенный в четырехмерном пространстве.

Однозначность и простота построения точек на поверхности в пространстве E⁴ достигаются благодаря следующим свойствам четырехмерного пространства [4, 5].

Свойство 1. Две плоскости общего положения в пространстве E4 (не вложенные в одну гиперплоскость) пересекаются только в одной точке.

Свойство 2. Если плоскость ω перпендикулярна гиперплоскости Г ′′(xyt), то ортогональная проекция ω ′′ плоскости ω на Г ′′ вырождается в прямую линию.

Присвоив узловым точкам контура произвольные координаты по оси t, получаем гиперэ- пюр, состоящий из двух трехмерных проекций контура w на «фронтальную» Г′(xyz) и «горизонтальную» Г′′(xyt) гиперплоскости проекций (рис. 2).

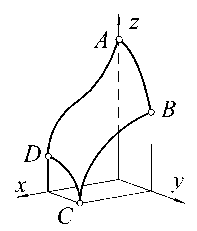
Рис. 1. Исходный контур

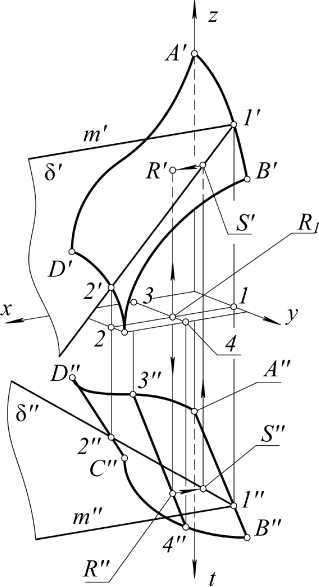
Рис. 2. Построение точки на поверхности

кости этого множества, в соответствии со свойством 2, вырождается в прямую линию 3′′-4′′ .

Таким образом, в результате выполнения второго действия в пространстве E⁴ определены два однопараметрических пучка плоскостей δ (12X_∞) и ω( 34Z_∞ ). Плоскости ρ и τ звеньев AD и BC принадлежат пучку δ, а плоскости σ и η звеньев AB и CD – пучку ω.

Действие 3 (построение точек пересечения вспомогательных плоскостей δ и ω ). Произвольная плоскость δ (12X_∞) из пучка δ _i пересекается с произвольной плоскостью ω( 34Z_∞ ) из пучка ω j в некоторой точке R (свойство 1).

Положение плоскости δ определяется координатой y , положение плоскости ω – координатой x , поэтому координаты x , y точки R зафиксированы выбором пары пересекающихся плоскостей δ и ω. Отмечаем на плоскости xy проекцию R₁ ( x , y ) точки R и по линии связи находим проекцию R′′ точки R на горизонтальной гиперплоскости проекций Г′′. Плоскость ω проецируется на Г′′ прямой линией 3′′-4′′ , поэтому R′′ принадлежит прямой 3′′-4′′ . Каждой точке плоскости xy соответствует единственная точка R(x,y,z,t) конструируемой поверхности в пространстве E⁴ . Проекция этой поверхности на гиперплоскость Г′ является решением поставленной задачи.

Оценка влияния управляющих параметров

В рамках алгоритма выделяются две группы параметров, влияющие на форму конструируемой поверхности. К первой группе относятся значения разностей координат узлов контура по оси t («глубина погружения» узлов в четвертое измерение). Задавая узлам ABCD разные координаты по оси t , получаем разные цилиндроиды в пространстве xyt (рис. 3, а , б ). При этом в исходном пространстве xyz получаем оболочки с незначительно отличаю-

Алгоритм построения поверхности в четырехмерном пространстве

Действие 1 (выбор базисной инцидентности). Пусть в пространстве E⁴ плоскости σ и η звеньев AB и CD пересекаются в несобственной точке Z_∞ оси z , а плоскости ρ и τ звеньев AD и BC – в точке X_∞ .

В этом случае, согласно свойству 2, звенья AB и CD проецируются на Г ′′ прямыми линиями A′′B′′ и C′′D′′ . Проекции на Г ′′ криволинейных звеньев AD и BC определяются по общему правилу: если линия принадлежит плоскости, то проекция линии принадлежит проекции плоскости.

Действие 2 (выбор пучков вспомогательных плоскостей). Поверхность – двупараметрическое множество точек, поэтому в пространстве E⁴ следует задать два однопараметрических множества (два пучка) вспомогательных плоскостей δ _i и ω j . В соответствии со свойством 1, любая пара плоскостей пересекается в точке. Двумерное множество точек R_i j = δ _i∩ ω j определяет в E⁴ некоторую поверхность.

Проведем гиперплоскость Δ³, параллельную xzt . Положение Δ³ в E⁴ вполне определяется одним параметром – координатой y . Отметив точки 1=AB ∩Δ³ и 2=CD ∩Δ³, выделяем вложенную в Δ³ плоскость δ (12∩m) , где m||x . Изменяя координату y гиперплоскости Δ³, получаем однопараметрическое множество плоскостей δ (12X_∞) . На гиперэпюре (см. рис. 2) проекции δ′ и δ′′ любой плоскости из этого множества параллельны плоскостям проекций xz и xt соответственно.

Проведем гиперплоскость Ω³, параллельную yzt . Ее положение вполне определяется координатой x . Выделим вложенную в Ω³ плоскость ω( 34Z ∞ ), где 3=AD∩Ω³ , 4=BC∩Ω³ . Изменяя координату x гиперплоскости Ω³, получаем однопараметрическое множество плоскостей ω( 34Z_∞ ). На гиперэпюре (см. рис. 2) проекция ω′′ любой плос-

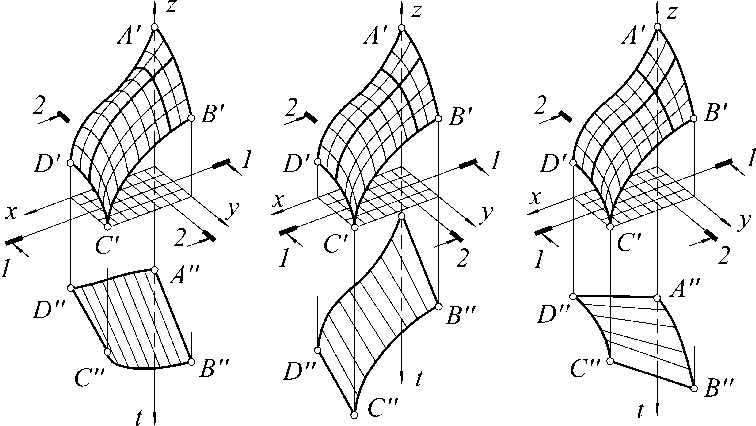
Рис. 3. Поверхность на четырехзвенном контуре

Научно-методический раздел

щейся степенью выпуклости, что указывает на малую чувствительность алгоритма к первой группе управляющих параметров.

Ко второй группе относятся параметры, определяющие варианты инцидентности плоскостей противолежащих звеньев σ∩η, ρ∩τ в четырехмерном пространстве. Например, на рис. 3, б показана поверхность с базисной инцидентностью σ (AB)∩ η (CD)=Z ∞ , ρ (AD)∩ τ (BC)=X ∞ . На рис. 3, в выбран существенно другой базис: σ (AB)∩ η (CD)=Y ∞ , ρ (AD)∩ τ (BC)=Z ∞ . При этом получаются незначительно отличающиеся поверхности (см. рис. 3, б , в ). Следовательно, вариация базисных инцидентностей слабо влияет на форму конструируемой оболочки.

На рис. 4 представлены продольное 1-1 и поперечное 2-2 сечения оболочек, натянутых на данный контур ABCD , для различных сочетаний управляющих параметров. Варианты а) и б) позволяют сравнить профили оболочек, полученные при одинаковой базисной инцидентности, но при разной «глубине погружения» узлов исходного контура в четырехмерное пространство.

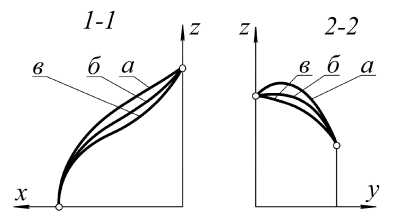
Рис. 4. Сечения оболочек

В варианте в) получена оболочка с малой выпуклостью в поперечном сечении 2-2 и со знакопеременной кривизной в сечении 1-1, для чего потребовалось изменить как «глубину погруже- ния», так и базисную инцидентность плоскостей противолежащих звеньев. Изменение управляющих параметров позволяет конструировать различные оболочки, натянутые на один и тот же замкнутый пространственный четырехзвенный контур.

Заключение

Предложен способ построения поверхности, основанный на выходе в четырехмерное пространство, отличающийся от известных использованием трехмерного гиперэпюра вместо плоского проекционного чертежа. Способ может найти применение в строительстве и архитектуре при проектировании оболочек, проходящих через заданный криволинейный контур.