Геометрическое моделирование поверхностных форм отгона виража автомобильной дороги на основе циклографического отображения

Геометрические параметры автомобильных дорог играют важнейшую роль в определении их транспортно-эксплуатационных качеств. Если геометрические параметры дороги не отвечают действующим нормам и требованиям, то эти ее недостатки нельзя исправить лучшими покрытиями полотна [1]. Автомобильная дорога является сложным строительным объектом и состоит из нескольких отличающихся друг от друга участков: прямолинейного в плане и виражного, при этом виражный участок, в свою очередь, делится на собственно вираж (круговой) и отгонные участки, служащие для плавного соединения прямолинейного в плане и кругового участков (рис. 1). По статистике наиболее аварийными участками автомобильных дорог являются различные поворотные участки, поэтому данные участки должны в максимальной степени отвечать установленным требованиям и нормам [2].

В современном проектировании и строительстве автомобильных дорог применяются различные подходы к их математическому моделированию [1, 3–7]. Все они ориентированы на рекомендации, приведенные в государственных нормах и правилах [2], согласно которым прямолинейный в плане участок дороги должен содержать дискретный каркас из типовых поперечных профилей, а на круговом участке дороги (вираже) – дискретный каркас из поперечных профилей в виде прямолинейных отрезков неизменного уклона. Известны математические модели, в которых автомобильная дорога рассматривается как объект, составные элементы которого, различаясь режимными и конструктивными характеристиками, стыкуются между собой по определенному порядку гладкости. Эти модели рассмотрены в работах [6, 7].

В работе [8] авторами рассматривается подход к формированию поверхностей проезжей части на прямолинейных участках на основе метода циклографического отображения. Виражи, а также переходные участки между ними и прямолинейными в плане, называемые отгонами, в работе [8] рассмотрены не были. В этой связи с целью развития и расширения возможностей предлагаемого авторами циклографического подхода в настоящей работе рассматриваются локальные особенности формирования поверхностных форм отгонов виражных участков автомобильной дороги.

Постановка задачи. Начальным этапом формирования любого участка автомобильной дороги является проектирование ее оси. Этот этап достаточно подробно рассмотрен в работе [7]. Будем считать ось дороги заданным геометрическим элементом, который представляет собой пространственную кривую не ниже порядка гладкости С ¹ [7, 9].

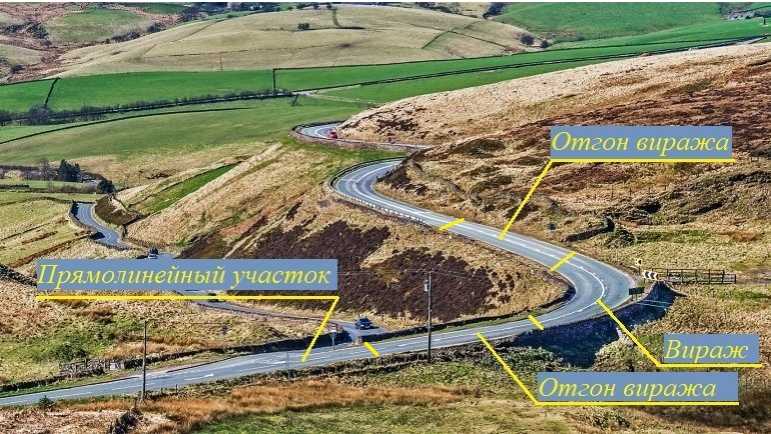
Рис. 1. Устройство автомобильной дороги на виражных участках

Задачу моделирования проезжей части автомобильной дороги на отгонном участке можно сформулировать следующим образом: задана ось дороги в виде гладкой, не ниже порядка гладкости С ¹, пространственной кривой P ( t ) , описываемой векторным уравнением:

P ( t ) = ( x ( t ), y ( t ), z ( t )); P '( t ) * 0; t e R : T_o <  t <  T . (1)

Требуется построить теоретическую поверхность отгонного участка автомобильной дороги.

Теория. Сущность циклографического метода заключается во взаимно однозначном отображении точек пространства R ³ на циклы в координатной плоскости ( xy ) декартовой системы координат Oxyz . Циклографический метод был предложен и развит немецкими геометрами W. Fiedler [10], E. üller и J. Krames [11]. Современный уровень развития циклографического отображения и его многочисленные теоретические применения и практические реализации изложены в работах [12–15].

Циклографическая проекция точки ( x, y, z ) пространства R³ представляет собой направленную окружность - цикл на плоскости (ху) с центром в точке (х, у) и радиусом R = |z|. Двум направлениям цикла соответствуют аппликаты z > 0 и z < 0. Следовательно, множество да³ точек пространства R³ можно поставить во взаимно однозначное соответствие с множеством да³ циклов плоскости (ху).

Рассмотрим циклографический образ оси дороги, представляющий собой пространственную кривую. Его получение основано на построении однопараметрического множества конусов, вершины которых принадлежат данной кривой, а основания (циклы) расположены в плоскости проекций (xy) и образуют однопараметрическое множество циклов [8]. Огибающая множества циклов будет являться циклографической проекцией пространственной оси дороги. Уравнения огибающей для изменяющихся значений полуугла β = β(t) при вершине конуса отображения имеют вид [8]:

x p (1,2) ⁽ t ) = x ⁽ t ) + ^{z (} t ) • ^{e (} t )

- x ( t )W)+ y ( t )7^^.

x ( t ) ______________^;

- x '( t ) • ц ( t ) ± x '( t ) 7 X ( t ) -ц ²( t )

У р (1,2) ⁽ t ) = У ^(t ) + ^{z (} t ) • e ⁽ t )

X ( t )

,

где Ц ( t ) = e ( t ) • z '( t ) + e '( t ) • z ( t );

X ( t ) = x '( t )² + y '( t )²; e ( t ) = tg ( P ).

Параметрические уравнения (2) описывают огибающую, которая может быть как единым объектом, так и состоять из ветвей P 3 (1) ( t ) и P 3 (₂) ( t ). Центры всех циклов образуют линию P ₁ ( t ) , представляющую собой горизонтальную проекцию исходной линии – оси дороги P ( t ) . Если принять (1) и (2) в качестве уравнений направляющих линий, то можно получить линейчатую поверхность, которая будет огибающей указанного однопараметрического множества конусов отображения с вершинами на пространственной кривой P ( t ) . Параметрические уравнения этой линейчатой поверхности имеют следующий вид:

X ⁽ t , l ) = x ⁽ t ) + l • [ ^x _P (i, 2) ⁽ t ) ^- x ⁽ t )];

Y ⁽ t , l ) = У ⁽ t ) ⁺ l • ^[ У p (i,2) ⁽ t ) ^- У ⁽ t )];                (3)

Z ( t , l ) = z ( t ) • (1- 1 );

t , 1 e R : T ₀<  t <  T , L ₀<  t <  L .

При рассечении поверхности (3) нормальными по отношению к линии P1 (t) плоскостями будут образовываться кривые линии с вершинами на исходной линии P(t) . Полученные линии сечений отличаются от общепринятых, соответствующих известным правилам и нормам [2]. Поэтому возникает необходимость преобразования получен- ной поверхности в другую линейчатую поверхность, сечения которой указанными нормальными плоскостями соответствовали бы общепринятым типовым нормам. Предлагаемое преобразование основано на «доворачивании» общей с линейчатой поверхностью (3) пары прямолинейных образующих каждого конуса отображения в нормальную плоскость линии P1 (t) . Это преобразование подробно рассмотрено в работе [8].

Общий принцип геометрического моделирования поверхностей дорожного полотна заключается в следующем. На плоскости проекций (ху) строится горизонтальная проекция оси дороги – линия P ₁ ( t ) . Затем по обеим сторонам этой линии строятся соответствующие ей линии – эквидистанты, удаленные от P ₁ ( t ) на расстояние, равное сумме полуширины проезжей части и обочины. После этого на полученных линиях как на направляющих строятся вертикальные цилиндрические поверхности. Линия пересечения такой цилиндрической поверхности и линейчатой поверхности проезжей части, построение которой основано на циклографической проекции, будет являться бровкой проезжей части. Циклографическая проекция бровки проезжей части позволяет получить новую линейчатую поверхность, которая при пересечении с вертикальной цилиндрической поверхностью обочины даёт бровку обочины дорожного полотна. Таким образом, создавая поверхность между осью дороги и бровкой проезжей части, получаем поверхность проезжей части, а между бровкой проезжей части и обочины – поверхность обочины.

Результаты эксперимента. Рассмотрим пример построения поверхностной формы автомобильной дороги на отгонном участке. Примем некоторые допущения:

– считаем известными граничные условия стыкуемых к рассматриваемому отгону виража и прямолинейного в плане участков дороги, а именно: координаты стыкуемых крайних точек на бровках дорожного полотна и обочин, а также значения первых и вторых производных их уравнений в стыкуемых точках;

– уклоны образующих прямых линий поверхностей проезжей части и обочины с целью наглядности заведомо увеличены относительно требуемых норм и правил [2];

– при моделировании отгона не рассматривается уширение проезжей части на подходе к виражу.

В качестве оси дороги рассмотрим кривую P ( t ) = { x ( t ), y ( t ), z ( t ) } с параметрическими уравнениями:

x ( t ) = 12 t ² + 36 t + 2, y ( t ) = 20 t^ + 9 t ² + 3 t + 3, z ( t ) = 10 + 3 t , t e [0,1].

Известно, что отгон виражного участка представляет собой элемент автомобильной дороги, на котором происходит переход от двускатного профиля к односкатному и наоборот [2, 3]. Автомобильная дорога, в свою очередь, состоит из поверхностей проезжей части и прилегающей к ней обочины. Условно отгон виражного участка можно разбить на несколько участков, схематично представленных на рис. 2. Деление на участки накладывает некоторые конструктивные ограничения, которые необходимо учитывать при проектировании отгона.

На первом этапе моделирования, соответствующем участку 1, поверхности отгона по внешней обочине придают уклон, равный уклону внешней половины проезжей части. Второй этап, соответствующий участку 2, характерен тем, что прямолинейные образующие поверхности внешней половины дорожного полотна, включая образующие обочины, вращают вокруг оси дороги до горизонтального положения. Третий этап, соответствующий участку 3, по существу является продолжением второго. При этом образующие поверхности внешней половины дороги продолжают вращать вокруг оси, пока не будет достигнут односкатный поперечный профиль с поперечным уклоном, равным уклону проезжей части на внутренней половине проезжей части. На четвертом этапе всю линию поперечного профиля, состоящую из внешнего участка обочины, внутренней и внешней проезжей части, вращают вокруг бровки внутренней проезжей части до создания требуемого поперечного уклона внутренней обочины.

Таким образом, формообразование линейчатых поверхностей на участках 1–4 основано

Рис. 2. Схема изменения профилей нормальных сечений поверхностной формы отгона нейной образующей поверхности на соответствующем участке. Отрезок прямолинейной образующей, как было отмечено выше, представляет собой профиль нормального сечения поверхности отгона. Изменение положения профиля происходит на основе его вращения в плоскости нормального сечения относительно точки пересечения нормальной плоскости и оси дороги.

Особенностью первого участка является то, что внешней обочине придается уклон, равный поперечному уклону проезжей части, при этом остальные элементы отгона не изменяются и имеют такие же постоянные уклоны, как и на прилегающем к отгону прямолинейном участке, и моделируются по вышеприведенному алгоритму.

Рассмотрим более подробно принцип формообразования поверхности на участках с переменным полууглом при вершине конуса отображения γ, γ = γ(t) (рис. 3). Фактически задача заключается в получении такой поверхности, которая бы не приводила к излому поверхности дороги в начале и в конце участка. В нашем случае к данному участку отгона прилегает с одной стороны прямолинейный участок дороги с двухскатным профилем, где угол наклона прямолинейных образующих поверхности обочины равен γ1, а с другой идет продолжение отгона, где у внешней поверхности обочины угол изменяется до угла γ2. Следовательно, можно получить две огибающие PY1(1) и PY2(1) циклов - оснований конусов циклографического отображения с полууглами при вершинах γ1 и γ2 соответственно. Решение задачи переносится на плоскость проекций (ху) и сводится к нахождению некоторой кривой, соединяющей начало огибающей P (1) с концом огибающей PY2 (1). Впоследствии данная кривая будет определять закон изменения угла наклона образующих поверхности обочины. Для получения такой кривой используется кубический сплайн, который позволяет добиться гладкости C1 в точках стыковки с кривыми соседних участков, что, в свою очередь, позволит добиться плавности стыковки получаемых впоследствии поверхностей обочины. Уравнение сплайна имеет вид [16]:

P ( t ) — а о + а_х t + a 2 t + a 3 t ,

где 1 1 <  t < 1 ₂ , t e R .

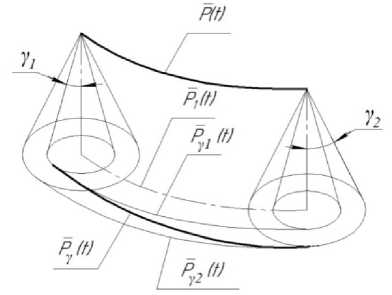
Рис. 3. К образованию линейчатой поверхности на участке с переменным полууглом при вершине конуса отображения

В рассматриваемом примере при углах γ₁ = 80° и γ₂ = 85° параметрические уравнения кривой P _Y ( 1 ) имеют вид:

x ( 1 ) — 3,5 + 42,6 1 + 54,4 1 ² - 67,2 1 ³;

y ( t ) — - 14,9 + 3,5 1 + 16,9 1 ² + 16,8 1 ³;

z ( 1 ) — 8,1 + 3 1 + 20,9 1 ² - 46,7 1 ³, где 0< t <0,3.

Уравнения полученной кривой P _Y ( 1 ) совместно с уравнениями оси дороги P ( t ) определяют уравнения линейчатой поверхности, которая и будет искомой поверхностью обочины с переменным углом y e [ y 1 , Y 2 ] наклона ее образующих. Дальнейшая обрезка данной поверхности вертикальной цилиндрической поверхностью внешней обочины позволяет получить линейчатую поверхность обочины на данном участке отгона (рис. 4).

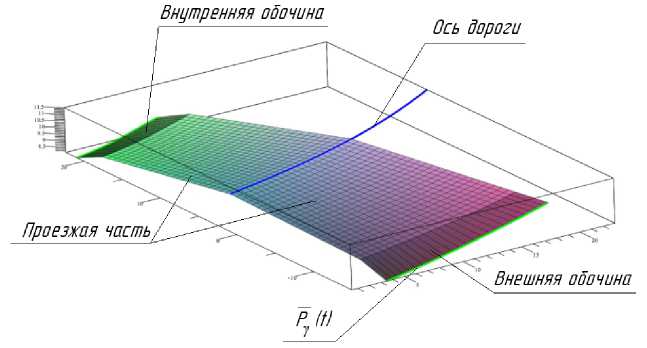
Рис. 4. Участок отгона с поверхностью внешней обочины, имеющей переменный угол γ наклона образующих

Параметрические уравнения этой поверхности имеют вид:

X ( t , l ) = 3,2 + 42,6 t + 32,3 t ² - 18 t ³ + (0,2 + 22,1 t ² - 49,2 t ³) • l , Y ( t , l ) = - 11,9 + 3,5 1 + 12,5 t ² + 26,6 t ³ + ( - 3 + 4,4 t ² - 9,8 t ³) • l , Z ( t , l ) = 8,9 + 3 t + 6,640"⁹ t ² - 2,2Ю ⁸ t ³ +

+ ( - 0,8 + 20,9 t ² - 46,7 t ³) • l , где 0 <  t < 0,3; 0 <  l < 1; t , l e R .

Оставшаяся внутренняя часть поверхности отгона, вплоть до четвертого участка, остается неизменной.

На четвертом участке при неизменном уклоне прямолинейных образующих поверхности обочины образующие прямые проезжей части начинают менять угол наклона до тех пор, пока не произойдет совпадение с углом наклона образующих внутренней поверхности обочины (см. рис. 2, участок 4). Это происходит за счет вращения образующих внутренней проезжей части вокруг ее бровки. Таким образом, полный внутренний поперечный профиль отгона преобразуется в одну прямую линию. Здесь применяется тот же метод, что и для создания поверхности обочины на первом участке при изменении ее угла наклона, схема которого представлена на рис. 3. Следует отметить, что при вращении образующих прямых вокруг бровки проезжей части происходит изменение оси дороги. Новая ось дороги может быть найдена следующим образом. Из ортогональной проекции оси дороги P ₁ ( t ) строится вертикальная цилиндрическая поверхность. Затем находится линия пересечения этой цилиндрической поверхности и линейчатой поверхности проезжей части с переменным углом наклона образующих. Полученная линия и будет «новой» осью дороги на данном участке (рис. 5).

Рассмотрим теперь моделирование поверхностных форм внешней части отгона виражного уча- стка. Сложность конструирования второго и третьего участков заключается в том, что при вращении прямолинейных образующих поверхности дорожного полотна достигается особое горизонтальное положение одной из образующих, в котором поперечный уклон равен 0. В циклографической проекции данное положение соответствует значению полуугла при вершине конуса отображения, равному 90°. Из (3) следует, что ветвь огибающей циклографической проекции в этом случае терпит разрыв в бесконечно удаленной точке. По этой причине построение поверхностных форм дорожного полотна на данных участках отличается от вышерассмотренных построений.

Выше было рассмотрено формообразование поверхности первого участка внешней части отгона (рис. 4). Для остальных участков внешней части отгона построим циклографическую проекцию оси дороги, имеющую неизменный полуугол при вершине конуса отображения до конца отгона. На полученной огибающей построим вертикальную цилиндрическую поверхность Ψ и линейчатую поверхность Ω , как показано на рис. 6. На цилиндрической поверхности необходимо определить несколько ключевых точек, по которым можно построить сплайны, определяющие подъем образующих линейчатой поверхности на конкретных участках отгона.

Каждая из ключевых точек лежит на границах между соответствующими участками отгона. Первая из ключевых точек – точка 1 – находится в плоскости проекций (xy) на первой образующей полученной линейчатой поверхности Ω . Для построения кубического сплайна между точками 1 и 2 имеем следующие условия: координаты точек T ₁ и T ₂ , значения первой T ₁ ' и второй T ₁ '' производных в точке 1, полученные из найденной ранее огибающей линии (циклографической проекции) с

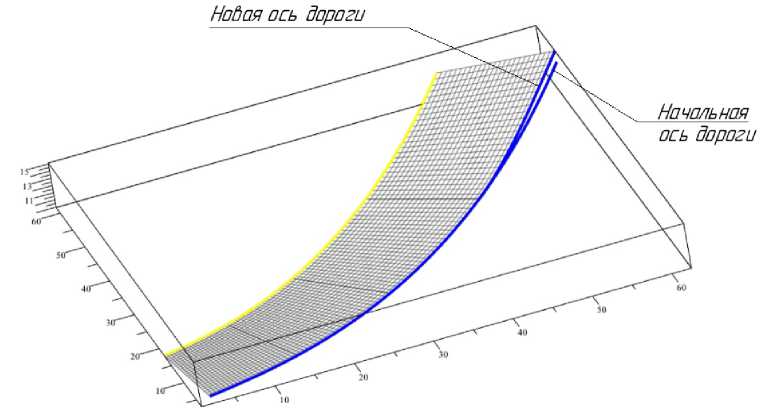
Рис. 5. Подъем оси дороги в конце отгона виражного участка

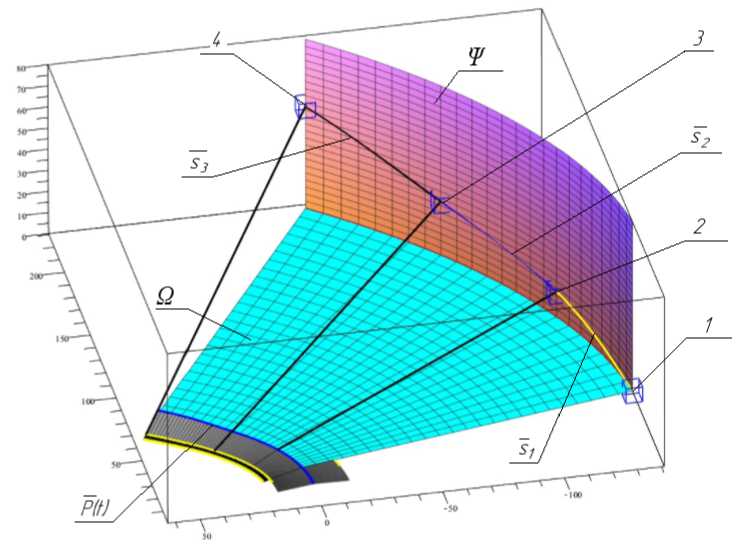
Рис. 6. Схема образования поверхности проезжей части внешней половины отгона виражного участка

первого участка. Эти четыре условия по формуле (4) позволяют найти кривую ^{s 1} , которая определяет изменение наклона образующих линий внешней поверхности проезжей части отгона на втором участке. При этом в точке 1 достигается гладкость стыковки C ² между циклографической огибающей предыдущего участка и линией s ₁ . В рассматриваемом примере уравнения кривой s ₁ имеют вид:

X s i ( 1 ) = 1,4 t ³ — 4,7 t ² + 66,2 1 + 60,7;

y_S 1 ( 1 ) = — 2,8 1 ³ + 13,8 1 ² + 6,3 1 — 141,2;

zS 1( t) = —1013 + 21,812, где 0 < 1 < 1.

Для нахождения точки 2 проведем горизонтальную прямую из последней точки второго участка до пересечения с цилиндрической поверхностью Ψ так, чтобы ортогональная проекция этой прямой была перпендикулярна ортогональной проекции оси дороги P ₁ ( t ) . Полученная точка и будет искомой точкой 2. Аналогичным образом, зная координаты точек T ₂ и T ₃ , а также производные T ₂ ' и T ₂ '' , строим кривую s ₂ , определяющую изменение угла наклона образующих для данного участка. Уравнения кривой ^{s 2} следующие:

x_{S 2} ( 1 ) = — 1,2 1 ³ — 2,8 1 ² + 61 1 + 123,6;

y_{S 2} ( 1 ) = — 2,6 1 ³ + 12,4 1 ² + 25,6 1 — 123,8;

Z s 2 ( t ) = — 0,13 t ³ + 2,7 t ² + 13,6 1 — 11,8, где 0 <  1 <  1.

Точка 3 находится на пересечении последней образующей третьего участка внутренней поверх- ности проезжей части и цилиндрической поверхности Ψ. Для определения кривой на этом участке имеем шесть граничных условий: T3 , T4 , T3 ' , T4 ' , T3 '' и T4 '' (для точки 4 в ходе принятых допущений принимаем известными параметры виражного участка, стыкуемого с рассматриваемым участком отгона). Для достижения второго порядка гладкости между точками 3 и 4 строим эрмитов сплайн пятой степени s3 , уравнение которого имеет вид [17]:

P ( t ) = a 0 + a_xt + a 2 t + a 3 t + a 4 t + a 5 t , где 1 1 <  1 < 1 ₂ , 1 e R .

Полученные в ходе вычислений параметрические уравнения кривой ^{s 3} имеют следующий вид:

x S 3 ( t ) = 48,9 1 ⁵ — 136,5 1 ⁴ + 105,4 1 ³ + 4,8 t ² + 25 1 + 180,6; y S 3 ( t ) = — 10,2 1 ⁵ + 40,6 1 ⁴ — 52,2 1 ³ + 33,8 1 ² + 33,8 1 — 88,4; z_{S 3} ( t ) = 41,5 1 ⁵ — 128,5 1 ⁴ + 114,1 1 ³ — 6,1 1 ² + 1,8 1 + 25,4, где 0 <  1 <  1.

Таким образом, полученные кривые между точками 1–4, состыкованные по второму порядку гладкости и рассмотренные совместно с соответствующими им участками оси дороги на отгоне виража, позволяют получить линейчатые поверхности. Отсекая данные поверхности вертикальной цилиндрической поверхностью E ( t,l ) внешней кромки проезжей части, как показано на рис. 7, получаем искомые поверхности проезжей части на внешней стороне дорожного полотна. Таким же образом получаем поверхности для внешней обочины.

Итоговая визуализация отгона виражного участка в рассматриваемом примере представлена на рис. 8. Для большей наглядности показаны насыпи, полученные путем построения циклографической проекции от бровок обочины.

Заключение

В работе рассмотрена возможность моделирования поверхностных форм отгона виражного участка на основе циклографического отображения.

Задаваясь осью дороги, можно получить модель отгона на виражном участке автомобильной дороги, состоящего из нескольких участков, соединенных между собой по условию гладкости. Полученная модель математически формализуема и допускает аналитические решения ее систем уравнений. Это делает предлагаемую модель доступной для использования в современных информационных технологиях проектирования поверхностных форм дорожного полотна.

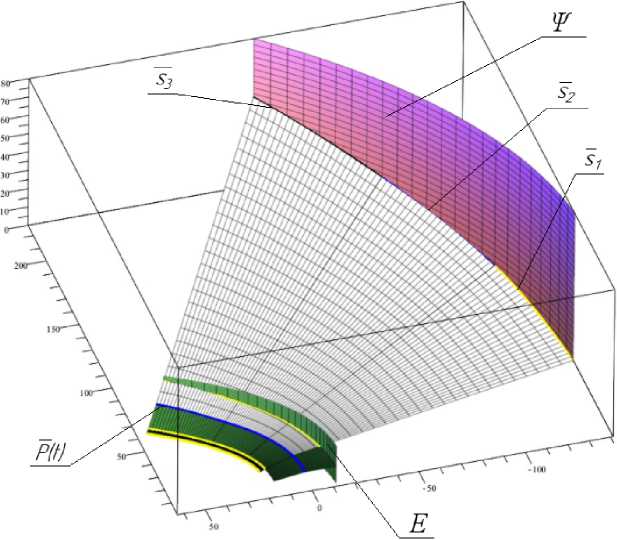
Рис. 7. Схема образования поверхности проезжей части внешней половины отгона виражного участка

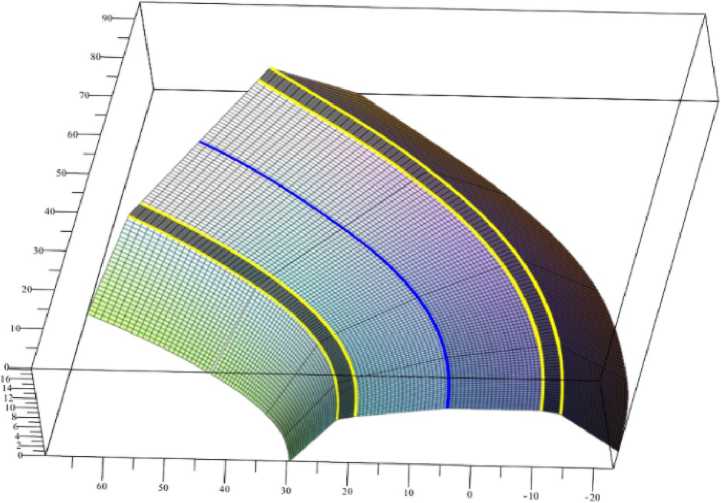
Рис. 8. Итоговая модель поверхностных форм отгона виражного участка