Геометрическое моделирование в задачах технической теории пластинок, связанных с параллелограммной областью

д.т.н.,

Общие сведения. Пластинки параллело- граммного очертания часто применяются в строительных и машиностроительных конструкциях в качестве несущих элементов мостовых конструкций, плит аэродромного покрытия, в виде элементов обшивки крыла и фюзеляжа самолёта, корпуса корабля. Точных методов расчёта таких пластинок не существует. Они рассчитываются приближёнными методами, как правило, численными, при использовании которых часто теряется физическая сущность задачи.

Для косоугольных пластинок предлагается провести оценку интегральных параметров с помощью геометрических методов расчёта.

К числу эффективных геометрических методов решения двумерных задач технической теории пластинок относятся изопериметрический метод (ИЗПМ) и метод интерполяции по коэффициенту формы (МИКФ), являющийся естественным развитием первого. Теоретические основы МИКФ разработаны одним из авторов этой статьи [1].

Геометрическое и физико-механическое моделирование параллелограммных пластинок. При сопоставлении геометрических фигур разных классов, например, круг и трапеция, эллипс и квадрат, как показали исследования [2], можно использовать интегральную характеристику формы фигур коэффициент формы, который выражается контурным интегралом:

K_fa=mm^, (1)

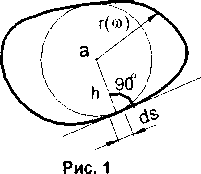
где h - перпендикуляр, опущенный на касательную к переменной точке контура (рис. 1). /^является количественной характеристикой «пра-

В статье кратко изложены основные результаты развития и применения метода интерполяции по коэффициенту формы к решению задач технической теории пластинок, связанных с параллеограммной областью. Показано, что, используя известные решения для па-раллеограммных пластинок (включая прямоугольные и ромбические) с однородными граничными условиями, приводимые в научной и справочной литературе, можно найти значения интегральных характеристик для любой па-раллелограммной пластинки.

вильности» (симметричности) областей и позволяет сравнивать их между собой.

Для областей с полигональным контуром формула (1) представляется в виде суммы:

^Kf_a = Z Т = £ (^ct8 ^{+ ct}§A)       (2)

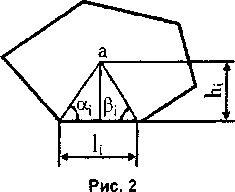
;=i"/     <=i где принятые обозначения указаны на рис. 2.

Из (2) для параллелограммов имеем:

Ку= 4(a/b + )>/a)/sina = 4(£_i+l/£₁)/sina, (3) где а и b - стороны параллелограмма; a - острый угол между сторонами; k_x = Vila - отношение высоты параллелограмма к длине основания. Из этого выражения как частные имеем: для прямоугольников -

Ку = 4(а/ b + Ы а) = 4(^+1/ к_х); (4) для ромбов -

(а = Ь) - К у = 8/sin а .                 (5)

Наиболее полные исследования изопериметрических свойств и закономерностей коэффициента формы приведены в работе [\].

Анализ выражений (3) - (5) позволил сформулировать изопериметрические теоремы относительно коэффициента формы для параллелограммов:

• -    из всех параллелограммов наименьшее значение Ку имеет квадрат;

• -    из всех параллелограммов равной высоты наименьшее значение Ку имеет прямоугольник, а наибольшее - ромб;

• -    из всех параллелограммов с одинаковым углом а наименьшее значение Kj имеет ромб.

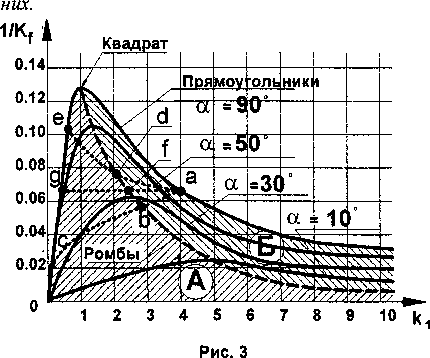
Графически эти теоремы представлены на рис. 3, где огибающая кривая, содержащая точки с, g, е и а, соответствует прямоугольникам, а кривая с точками d, f b - ромбам. Точки g и а соответствуют одному и тому же прямоугольнику. Линии e-d-a, g-f-a, c-b-f на рис. 3 изображают характер изменения Ку при различных геометрических преобразованиях параллелограмма. Из приведённых теорем следует, что область А, расположенная ниже пунктирной кривой, отображается на область Б и поэтому в дальнейшем можно рассматривать одну из

Для моделирования параллелограммных областей наиболее удобными будут аффинные преобразования. На рис. 4 представлены различные виды аффинных преобразований параллелограмма: на схеме а) изображён аффинный сдвиг прямоугольника; на схеме б) - одновременное аффинное растяжение и сдвиг прямоугольника, при которых вершины прямоугольника скользят по параллельным прямым, находящимися под углом к горизонту; на схеме в) - одновременное аффинное растяжение со сдвигом, когда вершины параллелограммов скользят по окружностям. Преобразуемые прямоугольники заштрихованы. На схемах а) и б) граничными фигурами являются прямоугольник и ромб, а на схеме в) - два пря- а)

в)

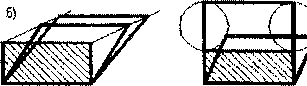
Рис. 4

моуголъника. Этим преобразованиям соответствуют кривые, изображённые на рис. 3 пунктирными линиями.

Сущность МИКФ. Если представить графически распределение всего известного из справочной литературы множества значений основных частот колебаний параллелограммных пластинок, например, с шарнирно опертым контуром (см. рис. 5ф в координатных осях 1/® - к\ и сопоставить рису. 3 и 5, то нетрудно заметить, что изображенные на них кривые подобны. Это говорит о том, что основная частота колебаний параллелограммных пластинок функционально связана с коэффициентом формы. Аналитическое доказательство такой зависимости приводится в монографии [\]. К сожалению, указанное подобие не носит линейного характера. Поэтому построение функциональных зависимостей F — Kf (F — интегральная физическая характеристика теории пластинок) сопряжено

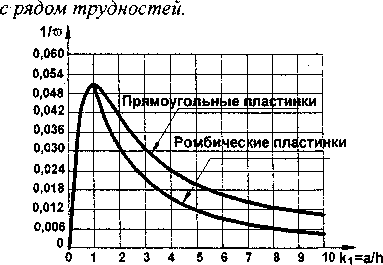
Рис. 5

Идея предлагаемого метода заключается в нахождении решений для пластинок, полученных в процессе какого-либо непрерывного (или дискретного) геометрического преобразования. При анализе форм пластинок этого множества следует выделить среди них хотя бы две, решения для которых F; и F^ известны (так называемые опорные или граничные решения). Используя их, искомое решение представляется формулой:

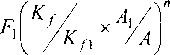
где параметр п определяется из выражения

Здесь Кр, А] - соответственно коэффициент формы и площадь для первой опорной фигуры; Кр, А2 - тоже для второй опорной фигуры. Вид функции (Т) предложен в работе [X] и соответствует естественному изопериметрическому виду, к которому приводятся известные точные решения задач строительной механики пла стинок.

Используя изопериметрические свойства коэффициента формы параллелограммов, сформулированы и доказаны изопериметрические теоремы относительно интегральных физических характеристик для рассматриваемых задач технической теории механики пластинок.

Коробко А.В., Малинкин Н.С.

Геометрическое моделирование в задачах технической теории пластинок, связанных с параллелограммной областью

Теорема 1. Всё множество значений интегральных характеристик в задачах технической теории пластинок, представленных в координатах F - К;И связанных с областями в виде параллелограмма, при однородных граничных условиях ограничено снизу (или сверху) значениями F для прямоугольных пластинок а сверху (или снизу) - ромбических.

Теорема 2. Из всех равновеликих параллелограммных пластинок одинаковой высоты прямоугольная имеет наибольшее значение w₀ но наименьшие - го, N_o, а ромб - наименьшее значения w₀, но наибольшие - го, N_o.

Теорема 3. Из всех равновеликих параллелограммных пластинок с однородными граничными условиями квадратная имеет наибольшее значение w₀, но наименьшие - со, N_o.

Теорема 4. Из всех равновеликих параллелограммных пластинок с однородными граничными условиями и одинаковым углом а ромбическая имеет наибольшее значение w₀, но наименьшие ~ to, N_o.

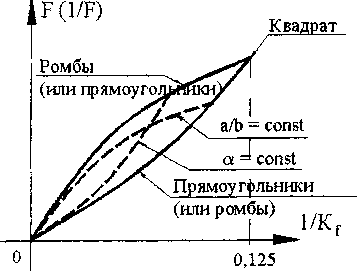
Рис. 6

Теорема 5. Из всех равновеликих параллелограммных пластинок с однородными граничными условиями и одинаковым отношением сторон прямоугольная имеет наибольшее значение Wo, но наименьшие - го, N_o.

Теоремы 1 - 5 иллюстрируются на рис. 6.

Определение интегральных характеристик с помощью МИКФ. Как отмечалось выше, граничными кривыми для параллелограммных пластинок являются кривые для прямоугольных и ромбических пластинок (рис. 5). Поэтому их можно использовать в качестве опорных пластинок при решении задач с помощью МИКФ.

Поскольку все параллелограммы равны между собой с точностью до аффинного преобразования, то любой параллелограмм может быть получен из квадрата, любого прямоугольника, любого ромба, любого другого параллелограмма.

Основные выводы

При геометрическом моделировании областей в форме параллелограмма с использованием МИКФ, получены следующие результаты:

• -    изучены закономерности изменения коэффициента формы параллелограммов при различных геометрических преобразованиях, в частности при аффинных преобразованиях, и доказаны изопериметрические теоремы; при этом выявлена область распределения интегральных характеристик параллелограммных пластинок в рассматриваемых задачах в зависимости от различных геометрических параметров параллелограммов (коэффициента формы, отношения сторон, отношения высоты к основанию) и установлены ограничивающие эту область кривые;

• -    построены граничные аппроксимирующие функции с использованием известных решений задач расчёта параллелограммных пластинок и разработаны различные способы определения интегральных физических характеристик параллелограммных пластинок с использованием этих кривых и известных решений.