Геометрическое описание функционирования производителя

В современной экономике рыночного типа, рассматривают такие случаи, как свободная конкуренция, монополия, олигополия и целый ряд других возможностей. «Отдельным производителем» при таком рассмотрении может оказаться как кустарь-одиночка, так и единственный монополист (в отрасли или в регионе). Но под отдельным производителем можно еще понимать агрегированного производителя, т. .е. вето отрасль целиком или даже группу отраслей, объединенных в некоторое единое и единственное производство.

Вопросы корректного агрегирования являются сложными и представляют большой самостоятельный интерес. В данной работе этот круг вопросов не рассматривается. Публикация посвящена, качественному анализу некоторых аспектов функционирования такого агрегированного производителя, как основного отдельного элемента, экономической системы. Для того чтобы яснее описать интересующие нас аспекты функционирования производителя, все рассматривается с максимальным упрощением. Анализ проводится в виде правдоподобных рассуждений с привлечением большого иллюстративного материала, что отражено в названии статьи. Такой подход связан, конечно, и с ограниченностью объема публикации. По той же причине не приводится обоснование корректности используемого метода и описание еще одного возможного графического представления, удобного для анализа, рассматриваемых ситуаций.

2.    Графический способ описания различных ситуаций

Будем исходить из того, что производитель в своей деятельности ориентируется на. такой экономический показатель, как прибыль. Более сложные ситуации, когда, производитель руководствуется не только соображениями максимизации прибыли, а. также объяснение такого его поведения, рассматриваются в [1].

Сразу понадобятся следующие обозначения:

п — объем произведенного и одновременно реализуемого продукта производителя, который зависит от цены продукта; с - цена, по которой реализуется данный объем продукта; т - себестоимость продукта, т. е. расходы на выпуск единицы продукта, которые находят свое возмещение в цене; г - прибыль производителя при реализации его продукта.

Надо отметить, что далее будет использоваться непрерывная зависимость себестоимости от объема выпуска (а затем, соответственно, и от цены). На самом же деле естественно ожидать, что для отдельного производителя при использовании данной технологии возможны лишь какие-то определенные, дискретные значения масштаба производства. Это обстоятельство не только не мешает необходимому анализу возникающих ситуаций, но даже облегчает такой анализ: ведь нужно будет просто перебрать несколько возможных дискретных вариантов вместо исследования (как правило, сложной) функциональной зависимости. Зависимость себестоимости от цены в виде непрерывной функции может иметь место и оказаться полезной при агрегировании многих производителей и, вполне вероятно, многих технологий в одного производителя. Кроме того, непрерывное представление этой зависимости позволяет удобным образом характеризовать характер изменения технологий в какой-то области производства, если для нее проведено соответствующее агрегирование.

Практически очевидно, что без возникновения чрезвычайных ситуаций, приводящих к проявлению эффекта Гиффина, объем приобретаемого продукта п(с) падает с ростом цены. В силу общеизвестного эффекта экономии от масштаба производства (см., например, [2] и более ранние работы) будем считать себестоимость также монотонно убывающей функцией объема производства: чем больше объем производства, тем ниже себестоимость. Формально эти утверждения имеют вид: dn/dc <  0, dm/dn < 0.

Общая прибыль произведенной продукции в простейшем случае г = (с — т)п зависит как от величины удельной прибыли с — т, так и от объема продажи продукта п. В силу этого целесообразно иметь зависимость себестоимости от цены (т.е. зависимость т(с)) с тем, чтобы определять величину прибыли при каждом значении цены как функцию цены. Цель и смысл перехода от зависимости т(п) к зависимости т(с) в том, чтобы вместо соотношения г = (с — т(п))п с двумя переменными (с и т(п) иметь со отношение г = (с — т(с))п с одной переменной (с).

Наглядное представление о способе построения такой зависимости дает рис. 1, на котором показано графическое изображение схемы численного метода построения зависимости т(с) по зависимостям п(с) и т(п).

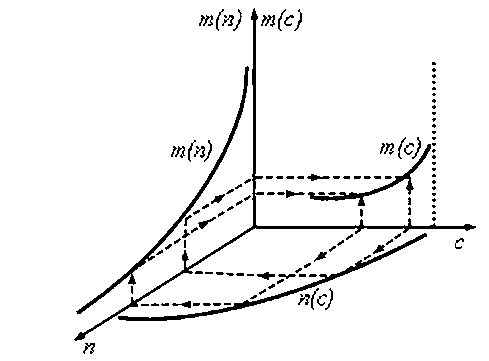
Рис. 1. Графическое представление схемы численного метода постороения зависимости т(с) по зависимостям п(с) и т(п)

Далее в тексте величины, помеченные звездочкой, будут относиться к максимальной прибыли.

Поведение удельной прибыли в случае изменения себестоимости при изменении цены показано на следующем рис. 2. На этом рисунке показана касательная L, имеющая угло- вой коэффициент наклона, равный 1. Нужна эта касательная, как это следует из содержательных и формальных соображений, для того, чтобы отделить область роста удельной прибыли от области ее падения.

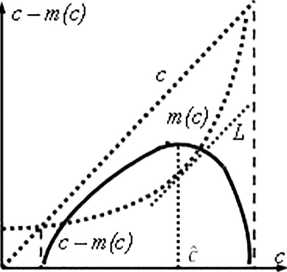
Рис. 2. Зависимость удельной прибыли от цены для себестоимости, меняющейся с объемом выпуска.

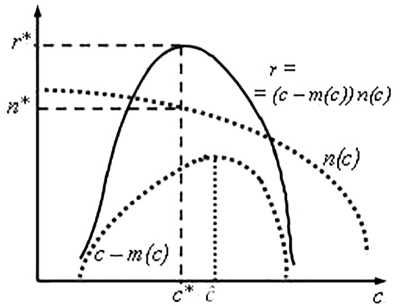
Рис. 3. Зависимость прибыли от цепы при себестоимости, меняющейся с объемом выпуска.

В самом деле: пока себестоимость т(с) растет медленнее, чем цена продукта с, удельная прибыль растет, при обратном соотношении между этими величинами удельная прибыль будет падать. Тот же результат даёт и необходимое условие экстремума, удельной прибыли d(c — m)/dc = 0. Цена (названная сс с крышечкой»), при которой удельная прибыль максимальна, показана на рис. 2 и рис. 3. На первом из них показано, что в соответствии с приведенными обоснованиями цене с отвечает со отношение dm/dc = 1.

На рис. 3 показана, и общая прибыль для рассматриваемого случая изменяющейся себестоимости. При одновременно падающих сомножителях (удельной прибыли с — m и спроса п) будет падать и произведение (т.е. т). Поэтому заведомо должно быть:

с* 6 С. (1)

Воспользовавшись тем, что (штрих — дифференцирование по цене) [т(с)] = [(с — т)п] = (1 — т)п + (с — т)п = 0 пр и с = с* и при т <  1, когда и т — 1 < 0, и п <  0, после преобразований получаем

с* = т + [п(т — 1)]/[п] >  т. (2)

Если бы в (1) имело место равенство, то в (2) в таком случае было бы т = 1 и получилось бы соотношение с* = т. Это означает обнуление удельной прибыли (а значит, и прибыли), что, как показано на. рис. 2, не имеет места. В итоге в (1) имеет место строгое неравенство.

3.    Последствия изменений технологии и спроса

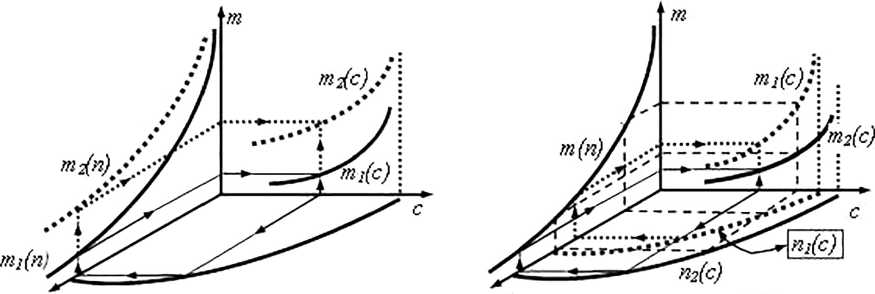
Значения конечных величин являются результатом «игры» спроса, и технологий. В силу этого приходится, в конце концов, рассматривать эти факторы совместно. Но начать, естественно, удобнее с раздельного рассмотрения влияния изменений спроса или технологии на себестоимость (точнее, зависимости себестоимости от цены). Проще всего воспользоваться иллюстрациями рис. 4 и рис. 5, которые базируются на рис. 1. На этих рисунках индекс 1 отвечает начальному состоянию, индекс 2 — конечному.

На рис. 4 наблюдаем практически очевидный результат «подъема.» кривой зависимости т(с) при переходе к технологии, которая влечет «подъем» кривой т(п), тем не менее этот рисунок приведен, так как он будет полезен в дальнейшем обсуждении. На этом же рисунке видно, каковы последствия снижения себестоимости (т.е. последствия перехода, от большой себестоимости т2(п) к меньшей себестоимости тЦп)).

Менее очевидный, но более приятный результат падения величин себестоимости (в зависимости себестоимости от цены) при росте спроса (рис. 5) объясняется смещением в области больших значений объема производства п, для которых себестоимость меньше. Как показано на этом рисунке, технология осталась неизменной, что отражено в неизменившейся зависимости т(п). Просто в новых условиях, при новом уровне спроса, производителю оказалось возможным перейти на более благоприятный участок функционирования, что дает доказуемый рост прибыли производителя. Обосновать это утверждение несложно.

Для величин т*(с) = ті(с)—Ат(с) и п*(с) = п1 (с)+Ап(с), в которых Ат(с), Ап(с) > 0, получаем: т* = (с — т*)п* = (с — т1 + Ат(пі + А(п) = (с — ті)пі + (с — т1)Ап + Атпі + +АтАп = ті + (с — ті + Ат)Ап + Атпі = ті + (с — т*)Ап + Атпі > ті пр и с > 0, так как все слагаемые в последней сумме положительные. Из этого следует, что т* = т + 1(с*) > т*(с*) = т* + (с* — т*(с*))Ап(сі) + Ат(с1)пі(с*) > т*. (3)

п                                   И

Рис. 4. Влияние изменения технологии             Рис. 5. Влияние изменения спроса, на зависимость себестоимости от цены (т(с))    на зависимость себестоимости от цены (т(с))

О соотношениях между ценами и объемами выпусков, максимизирующих прибыль производителя, можно сказать, только зная конкретные зависимости между величинами опросов и себестоимостей.

Опишем, как сработают оба. описанных фактора. Будем понимать под мощностью производителя максимально возможный объем выпуска, его продукции.

Изменение зависимости т(с) при росте спроса и (условном) росте себестоимости показано на рис. 6, причем с учетом роста мощности производства (М* > Мц индекс 1 — начальное состояние). Уточним, что означает «условный» для роста, себестоимости. Как видно на указанном рисунке, первоначально невозможно производить больше, чем Мі, так как таковы мощности производства. В силу этого цена, произведенного продукта, не может быть меньше той, что обозначена как с+. Аналогично для новой технологии и нового спроса цена не может быть меньше с+. Но в новых условиях, во-первых, оказываются доступны новые объемы производства с себестоимостью как функции от объема выпуска п, меньшей, чем раньше. Во-вторых, зависимость т(с) уже имеет меньшие значения, чем раньше. Поэтому рост себестоимости как функции только объема, выпуска, был назван условным.

В соотношении, определяющем величину прибыли, фигурирует удельная прибыль (с — т, т. е. прибыль в расчете на единицу продукции), посмотрим, что происходит с ней.

Результат изменения удельной прибыли с — т от индекса 1 к индексу 2 при изменении и спроса, и технологии, и мощности производства, приведен на. рис. 7. На этом рисунке показано, что, во-первых, удельная прибыль отлична, от нуля не для всех значений цены. Во-вторых, переход на. новую технологию, связанную с ростом спроса, может расширять область цен, представляющих интерес для производителя. В-третьих, в новых условиях значение удельной прибыли может возрастать.

Характер возможных изменений, обусловленный ростом спроса, и сменой технологии, иллюстрируют рис. 8а, б и рис. 9а, б.

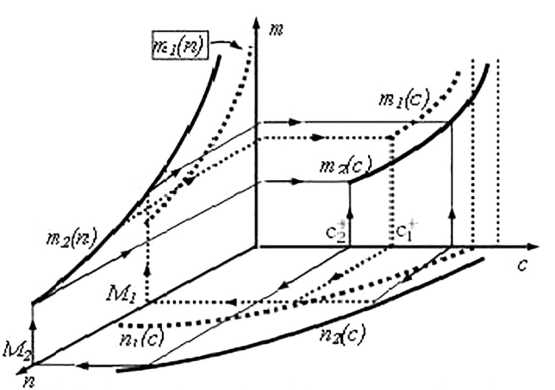
Рис. 6. Влияние изменения спроса и технологии на зависимость себестоимости от цены ( m ( e )^

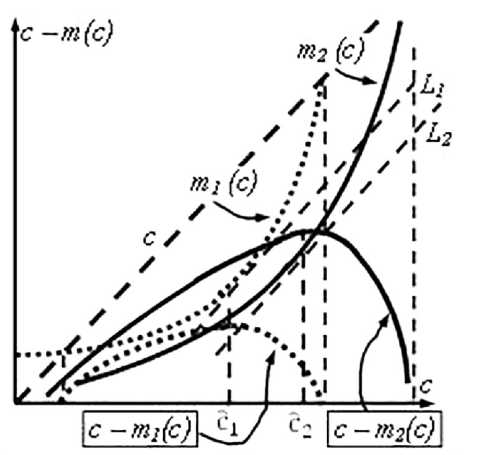
Рис. 7. Зависимости удельных прибылей от цены для себестоимостей, меняющихся

с объемом выпуска

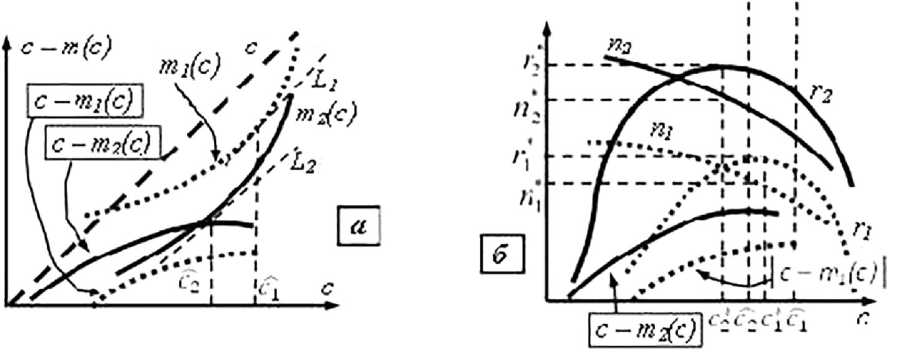
Рис. 8. Вполне вероятный результат роста спроса и смены технологии в случае соотношения

dm 2 /de > dm 1 /de

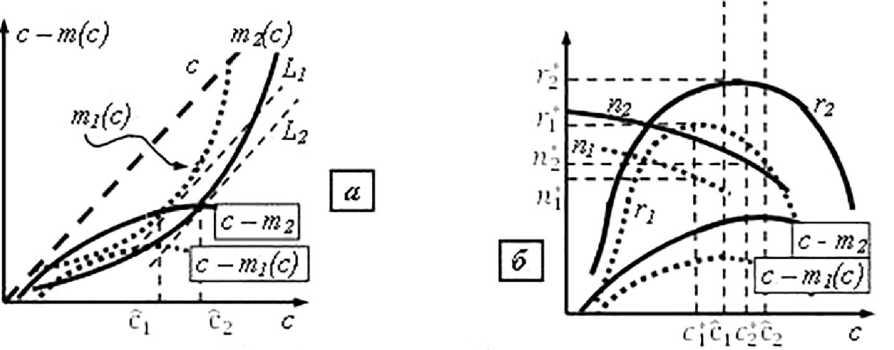
Рис. 9. Вполне вероятный результат роста спроса и смены технологии в случае соотношения dm 1 /de > dm 2 /de

Первый из них, рис. 8а, соответствует более быстрому росту новой себестоимости по сравнению со старой ((dm2/de) > (dmi/de)), когда оказываете я, что имеет место С2 < с1. В этом случае, возможно, будет также иметь место: e2 < ep Такая возможность обусловлена строгим неравенством в соотношении (1) и показана на рис. 86. При реализации такой возможности будет рост объема выпуска ( п2 = П2(с2) >  пДсі ) > ni(e1) = пД, и рост прибыли по произведенной продукции (обоснования аналогичны тем, которые привели к результату (3)).

Ситуация, когда имеет место соотношение (dm1 /de) > (dm2/de) т.е. более быстрого роста старой себестоимости по сравнению с новой, показана на рис. 9а. Указанное условие означает, что имеет место С2 > ci. В этом случае, скорее всего, будет c2 > cG как это показано на рис. 96, рост объема выпуска и рост прибыли по произведенной продукции. Такое предположительное заключение может быть уточнено при использовании конкретных зависимостей всех величин.

В современных исследованиях большое внимание уделяется моделированию и анализу социальных процессов. В качестве примера сошлемся на публикацию [3]. Продемонстрируем применение предлагаемого геометрического подхода для описания различия последствий того, чей спрос (бедных или богатых) претерпел изменение. Разделение на бедных и богатых можно провести по характеру изменения их спроса при изменении цен в разных диапазонах. Считается, что спрос бедных изменяется в области малых цен, в то время как спрос богатых изменяется в области больших цен.

4.    Последствия изменения спроса бедных

На рис. 10 переход от 1 к 2 — это падение спроса бедных при неизменном спросе богатых и неизменной зависимости т(п). На рис. 11 показан один из возможных случаев последствия такого перехода. Следствием указанного изменения спроса будет такое изменение зависимости себестоимости от цены, при котором в области небольших цен себестоимость возрастет. На рис. 10 цена c_G отделяет область единой зависимости спроса от цены пу от области с различными уровнями спроса ni(c) и 712(c). Первая — сплошная линия, вторая — точечный пунктир.

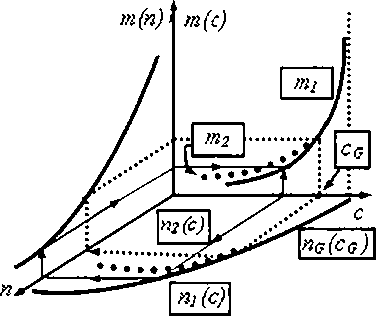
Рис. 10. Последствия изменения спроса, бедных при неизменных спросе богатых и зависимости т ( п )

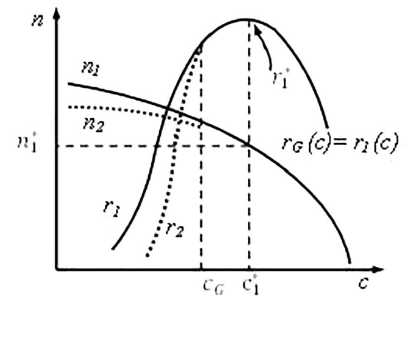
Рис. 11. Результат изменения спроса, бедных при c l > c _G

Обратный переход соответствует росту спроса, бедных при неизменном спросе богатых и неизменной зависимости т(п).

При c < c_G, m₂(c) > m₁(c) и n1(c) > n₂(c) очевидно получается:

r₂(c) = (c — т + 2)n2 <  (c — т1 )п1 < (ci — m(c1))n1 = r*.               (4)

Возможны два. варианта, последствий описываемого изменения спроса, бедных.

Пусть первоначально имело место соотношение Ci <  c_G. Это случай, когда максимальная прибыль производителя определяется спросом, если не богатых, то достаточно состоятельных людей. Тогда, получится ситуация, показанная на. рис. 11. В силу (4) максимума, прибыли в новой ситуации при c < Cy быть не может. Если же c > Cy, то новая ситуация ничем не отличается от исходной. Значит, для производителя никаких последствий падение спроса, бедных при неизменном спросе богатых (состоятельных) и неизменной зависимости т(п) в данном случае не будет. Производитель не будет изменять ничего в своем производстве, и ничего не изменится для потребителей.

Надо отметить, что продемонстрированное изменение спроса без каких-либо последствий имеет место в силу того, мы исходили не только из фактического спроса, но и из намерений потребителей, поскольку использовали зависимость спроса от цены.

Совсем иными будут последствия изменения спроса бедных, если изначально окажется, что с1 <  c_G.

В рассматриваемом случае для V с < CG между величинами прибыли будет иметь место соотношение (4), что означает падение максимальной прибыли производителя в новых условиях. Что же касается вероятного варианта изменения цены с*, соответствующей максимальной прибыли производителя, то вполне допустимо предположить возрастание этой величины, как показано на рис. 12. Конкретный результат зависит от реального соотношения всех величин.

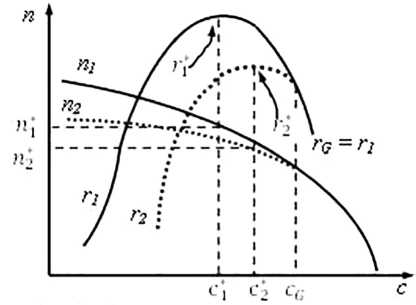
Рис. 12. Последствия изменения спроса бедных при с * < c _G

Случай возрастания спроса бедных при неизменном спросе богатых и неизменной зависимости себестоимости от цены можно рассмотреть аналогичным образом. Этот случай оказывается намного благоприятнее как для производителя, так и для потребителей. Падение спроса бедных при неизменном спросе богатых вполне может сопровождаться ростом себестоимости (в результате общего роста цен производственных затрат, например), как это показано на рис. 13. Естественным следствием этих изменений будет рост всех значений себестоимости в зависимости этой величины от цены, см. указанный рисунок. Причем никакой общей части в зависимости т(с), как это было в предыдущем случае, уже не будет, следствием чего окажется результат, показанный на рис. 14.

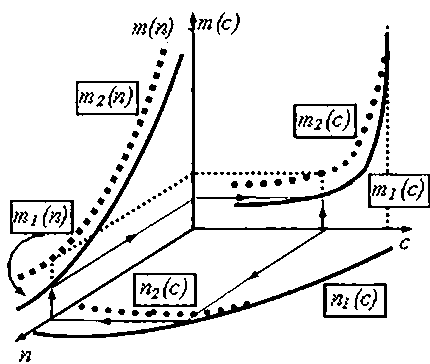
Рис. 13. Результат изменения спроса, бедных при неизменном спросе богатых и росте т(п)

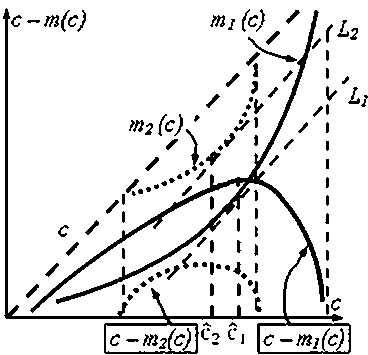
Рис. 14. Эффект одновременного падения спроса, бедных и роста, себестоимости производства.

На последнем указанном рисунке также показано уменьшение диапазона цен, при которых с — т* >  0. Это практически обязательно повлечет уменьшение с* по сравнению с С1. Следствием этого, в лучшем случае, будет уменьшение цены с*, максимизирующей прибыль в новом состоянии, по сравнению с аналогичной ценой с*. Не исключено также, что может оказаться п*_ > п*. Но при п* < пі, с — т* < с — ті обязательно будет г* < г* что повлечет г* >  г*.

Не лишне рассмотреть и ситуацию, когда падение спроса бедных и уменьшение себестоимости имеют место одновременно. Такой случай может быть показан на рис. 13 в результате замены сплошных линий на пунктирные и наоборот вместе с переименованием всех величин. Теперь зависимость т(с) «смещается вниз», т. е. себестоимость производства уменьшается. Следствием этого будет рост удельной прибыли производителя с — т(с). Для данного случая изменения величин с*,п* и г* будут обратными по отношению к предыду щему случаю.

Разумеется, изменяться может и спрос богатых. Эта ситуация описывается в следующем разделе.

5.    Последствия изменения спроса богатых

Если при неизменных спросе бедных и технологии падает спрос богатых (т. е. имеет место переход от 1 к 2 в области больших цен), то изменение зависимости т(с) будет таким, как показано на рис. 15.

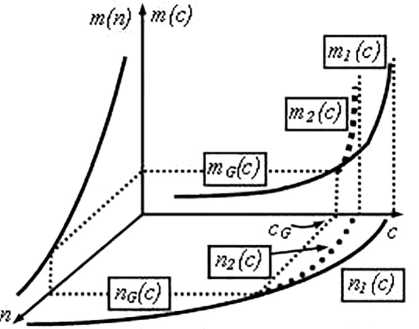
Рис. 15. Результат изменения спроса богатых при неизменных спросе бедных и зависимости т(п)

Следствием падения спроса будет такое изменение зависимости себестоимости от цены, при котором в области больших цен и малых объемов выпуска себестоимость возрастет. На рис. 15 цена Су отделяет область единой зависимости спроса от цены (область пу) от области с различными уровнями спроса пі(с) и п*(с). На указанном рисунке сразу видно, что сужается диапазон цен, выбираемых потребителями.

Обратный переход соответствует росту спроса богатых при неизменном спросе бедных и неизменной зависимости т(п).

При с> Су имеем соотношения: т*(с) > ті(с) (но! только в той области цен, в которой определены ненулевые значения себестоимости) и пі(с) >  п*(с). Используя эти соотношения, вновь получаем для области цен с различными себестоимостями соотношение (4). Из этого соотношения следует, что при любой локализации цены, максимизирующей прибыль производителя после падения спроса богатых (и неизменных спросе бедных и т(п)), будет г* 6 г*.

Рассмотрим возможные варианты соотношений между различными величинами.

ПЕРВЫЙ ВАРИАНТ.

Пусть первоначально имело место соотношение el <  cq. Это случай, когда максимальная прибыль производителя определяется спросом бедных и, возможно, какой-то частью достаточно состоятельных людей. Тогда получится ситуация, показанная на рис. 16. В силу (4) максимума прибыли теперь при с > e_G быть не может. При с < e_G новая ситуация ничем не отличается от исходной. Значит, никаких последствий падение спроса богатых при неизменном спросе бедных (состоятельных) и неизменной зависимости ттг(п) в данном случае не будет. Производитель не будет изменять ничего в своем производстве.

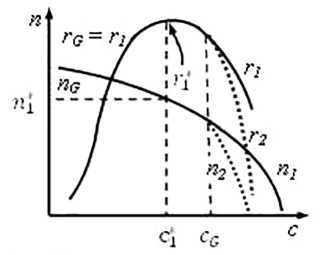
Рис. 16. Последсвия изменения спроса, богатых Рис. 17. Последсвия изменения спроса, богатых при с 1 <  c _g                                     при с 1 >  c _g

ВТОРОЙ ВАРИАНТ.

Иными будут последствия изменения спроса, богатых, показанные на. рис. 17, если изначально окажется, что имело место соотношение с1 >  cq.

В рассматриваемом случае для Vc >  c g между величинами прибыли будет иметь место соотношение (4), что означает падение максимальной прибыли производителя в новых условиях.

На рис. 17 показан случай такого изменения спроса, богатых (и, похоже, состоятельных покупателей), в котором имеет место достаточно резкое падение прибыли производителя. А именно: в новых условиях прибыль производителя т * (с) <  t * ( c g ) дл я V c >  cq. Для потребителей достоинством данного случая является то, что возрастает объем выпуска, и уменьшается цена, заинтересовывающая производителя (т.е. цена с*, максимизирующая прибыль производителя, которая на рис. 17 показана равной e_G).

При всевозможных конкретных соотношениях между зависимостями разных величин, определяющих конечные результаты, эти результаты могут быть и другими. Речь идет о следующем.

Если имеет место соотношение c g < с* < с*, то для производителя и потребителей это означает: и t * ( c g ) >  т * <  т * и n* < n* < n(e_G). Какой-то выигрыш получат потребители, производитель проигрывает. Не исключено, что, учитывая конкретные обстоятельства, производитель вообще не станет реагировать на. изменение спроса.

ТРЕТИЙ ВАРИАНТ.

Если имеет место соотношение c g <  с* < с*, то для производителя и потребителей это означает: и t * ( c g ) <  т * <  т* и n* <  n* < n(e_G). Какой-то выигрыш, может быть, получит производитель (меньше надо производить), потребители проигрывают и в цене, и в объеме продукции. Не исключено, конечно, что с учетом конкретных обстоятельств производитель не станет реагировать на. изменение спроса, (скажем, не захочет сокращать производство, чтобы не увольнять работников и/или не терять какую-то часть рынка).

Для того чтобы лучше увидеть, когда, какой из трёх перечисленных вариантов реализуется, воспользуемся рис. 18 — А, В.

Случай, показанный на рис. 18 А. когда с* < Ci < e_G, соответствует первому варианту, описанному выше. Как уже было сказано, никаких изменений не произойдет.

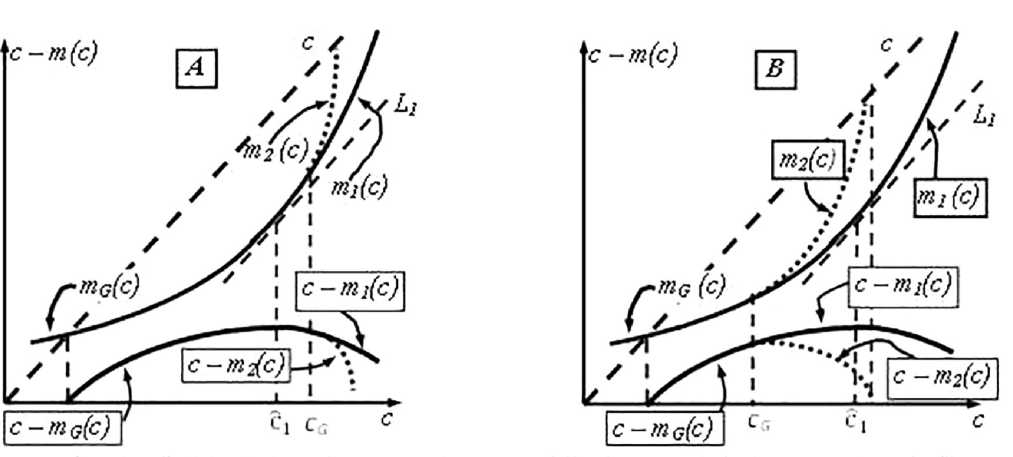
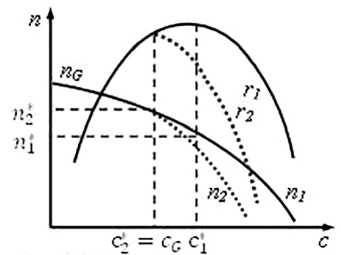
Рис. 18. Разные варианты падения спроса богатых при неизменных спросе бедных и т ( п )

Если имеет место случай, показанный на рисунке В (т.е. монотонное падение удельной прибыли при c_G<  сД, то получится второй вариант, описанный выше, причем будет ^С2 = ^c_G.

Если будет вариант рисунка В при C g < ci < С2 < С1 и удельна я прибыль с — т₂ (с) будет расти при C g < с < С2, то становится возможным третий из описанных выше вариантов. Выполнение условия ci < С2 является в данном случае обязательным, так как иначе получается вариант с2 < С2 < сД

Наконец, если будет вариант, показанный на рисунке В, но одновременно будет ci <  Cg, то получаем с2 = с*.

Понятно, что при противоположном развитии ситуации, т.е. при росте спроса богатых и неизменных спросе бедных и зависимости себестоимости от цены, результаты будут противоположными описанным выше.

Падение спроса богатых при неизменном спросе бедных вполне может сопровождаться ростом зависимости себестоимости т(п), что и показано на рис. 19. Следствием этого будет рост всех значений себестоимости в зависимости этой величины от цены, см. указанный рисунок. Как и в случае падения спроса только бедных и роста себестоимости, появляются две не совпадающие даже частично зависимости т(с), причем новая зависимость проходит «выше» старой. Все значения себестоимости в новой зависимости т(с) оказываются больше, чем в исходной.

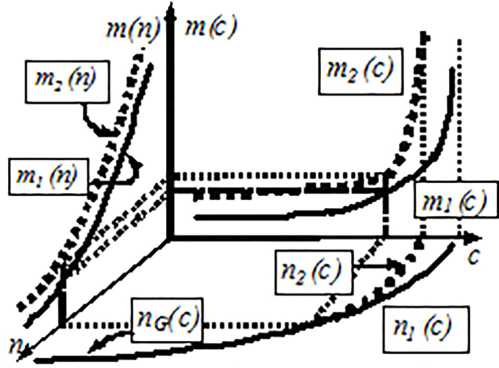
Рис. 19. Результат изменения спроса богатых при неизменном спросе бедных и росте т ( п )

Дальнейшие рассуждения полностью аналогичны тем, которые проводились в случае падения спроса только бедных при росте или падении себестоимости. Для описания по- следствий рассматриваемых изменений можно восполвзоватвся рис. 14. Окончательный резулвтат изменений спроса и себестоимости, как и ранвше, будет зависеть от конкретных значений исходных величин.

6.    Заключение

В данной публикации в силу ограничения по ее объему изложен не весь имеющейся материал. Но более важным является то, что все ситуации рассматривались в условиях полной определенности и известности всех исходных данных. Такая идиллия, конечно, места не имеет. Тем не менее, изложенные результаты могут представлять определенный интерес, поскольку дают качественное представление о том, что происходит и оказывается возможным для производителя при его функционировании.