Геометрическое описание функционирования производителя - 2

Считается, что одним из наиболее ранних примеров трёхмерной научной визуализации была термодинамическая поверхность Максвелла [1]. К настоящему времени научная визуализация как метод анализа научных данных и их рационального представления стал уже широко применяемым приемом в самых разных исследованиях. Этот подход использован и в предлагаемой работе автора.

Данная публикация является логическим продолжением предыдущей публикации автора [2]. В указанной статье описан достаточно простой способ наглядного представления соотношений, необходимых для качественного анализа функционирования отдельного (или агрегированного) производителя. Суть этого геометрического способа будет видна из приведенных далее рисунков. Смысл его использования в том, что он позволяет иметь дело с зависимостью всего лишь от одной переменной.

Упомянутая возможность использования геометрического описания для анализа функционирования агрегированного производителя подразумевает, что удается провести такое агрегирование. Этот круг вопросов в данной статье не рассматривается. В качестве примера реализации такой процедуры сошлемся на работу [3].

Далее используются следующие обозначения:

п — объем произведенного и одновременно реализуемого продукта производителя, который зависит от цены продукта; c — цена, по которой реализуется данный объем продукта; m — себестоимость продукта, т.е. расходы на выпуск единицы продукта, которые находят свое возмещение в цене; г — прибыль производителя при реализации его продукта.

Считается, что имеют место соотношения: (dn/dc) <  0; (dm/dn) <  0. Величины, помеченные верхней звездочкой, будут относиться к максимальной прибыли. Величины, помеченные нижней звездочкой, будут относиться к максимальному доходу. Дополнительные обозначения будут вводиться по мере их появления.

2.    Последствия одновременного изменения спроса бедных и богатых при неизменной зависимости m(n)

В данной статье использовано не такое зрелищное представление построения величины m(c), как в предыдущей, но все действия полностью аналогичны ранее описанным.

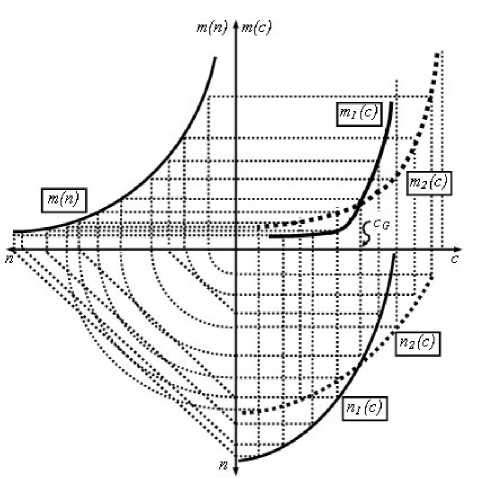
Рис. 1. Последствие одиовремеииого изменения спроса, бедных и богатых

Случай одновременного и однонаправленного изменения спроса, и богатых, и бедных (скажем, возрастает спрос у всех) обсуждается в предыдущей публикации автора. Теперь на. рис. 1 показан случай падения спроса, бедных и возрастания спроса, богатых (переход от сплошных линий с индексами 1 к пунктирным с индексами 2). Ясно, что этот же рисунок можно трактовать и как возрастание спроса, бедных с одновременным падением спроса, богатых, для чего достаточно переименовать кривые. На этом же рисунке показана цена c_G, при которой n1(c) = n₂(c), m 1 (c) = m₂(c).

Полученное представление m(c) оказывается полезным для первичного ограничения области, в которой может находиться цена продукта c*, отвечающего максимуму прибыли. Удельная прибыль р = c — m(c) растет до тех пор, пока рост цены не меньше роста себестоимости. При спросе, монотонно убывающем по мере роста, цены, прибыль заведомо будет падать при падающей удельной прибыли. Ситуация показана на рис. 2, на котором цена с — граница, между ростом и падением удельной прибыли. Эта. цена, соответствует угловому коэффициенту 1 касательной L к графику зависимости себестоимости m(c).

В [2] показано, что имеет место строгое неравенство с * < с, если производитель работает с положительной прибылью, см. рис. 3.

Как и раньше, интерес представляют изменения экстремальных значений с, пит. Даже при не изменившейся зависимости m(n) оказываются возможными несколько вариантов изменения значений этих величин.

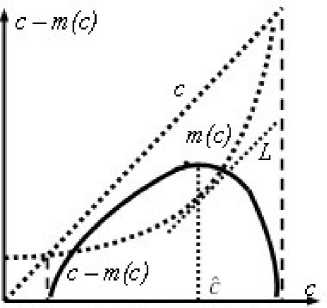
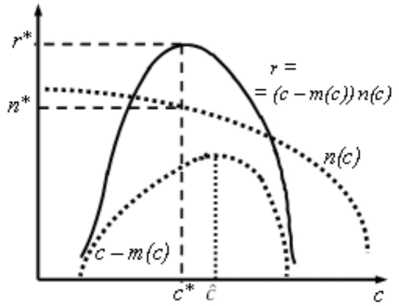
Рис. 2. Зависимость удельной прибыли от цены Рис. 3. Зависимость прибыли от цены при себе-себестоимости, меняющейся с объемом выпуска стоимости, меняющейся с объемом выпуска

Прежде всего, надо отметить, что невозможна реализация двух соотношений между значениями величин Ci, С2 и cG.

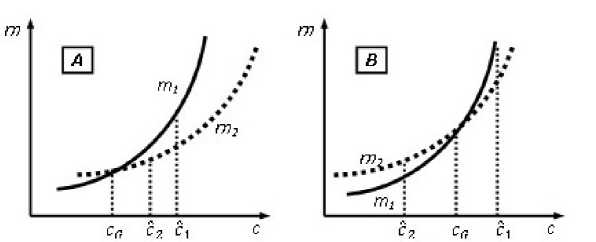
Рис. 4. Невозможные соотношения значений c_e, С 1 и с ₂

Невозможно соотношение с_G< C2 < Ci, показанное на рис. 4А. В самом деле, если для m 2 касательная при C2 имеет угловой коэффициент 1, то явно быстрее растущая при этом значении аргумента кривая mi должна иметь в этой точке угловой коэффициент больше единицы. А это означает, что для соответствующего значения Ci должно быть Ci < C2.

Второе невозможное соотношение показано на рис. 4В. В самом деле, угловой коэффициент для mi меньше единицы и при С₂, и при c_G, в то время как угловой коэффициент m2 при этих значениях цены не меньше единицы. Выполнение же указанного соотношения означает тем не менее, что mi растет быстрее, чем m2, и «догоняет» m2 , не успев начать расти быстрее, чем m2.

Соотношение С2 < Ci может иметь место только в одном случае, при С2 < Ci < cG, как показано на рис. 5.

Повторив уже использовавшиеся рассуждения, получаем следующее.

При c <  c_g имеем соотношения: m2 (с) > mi (с) (в той области цен, в которой определены ненулевые значения себестоимости) и ni (с) > пДс). Значит, для вс ей области цен c <  c_G:

Г 2 (c) = (c - m2 )n 2 < (c - m i )n i <  (ci - mi(ci))ni = r * . (1)

Из этого соотношения следует, что при любой локализации цены, максимизирующей прибыль производителя после падения спроса бедных и возрастании спроса богатых (при неизменной зависимости m(n)), r * 6 r *. Возможно (но это лишь возможность), произойдет снижение цены c*, доставляющей максимум прибыли производителю. А вот снижение соответствующей величины объема выпуска п * произойдет обязательно, так как в указанной области цен будет иметь место n₂(c) < n_i(с).

Хотя рассматривается ситуация неизменной зависимости m(n), возможным является изменение себестоимостей m(c). При этом может иметь место соотношение C 2 > С. Допустимые варианты показаны на рис. 6А, В, С.

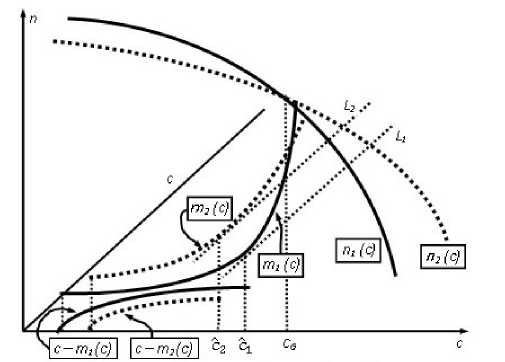
Рис. 5. Возможное соотношение c_G, щи с ₂

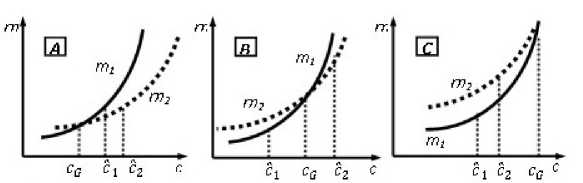
Рис. 6. Возможные соотношения значений c_G, С 1 и С 2

Для первого из этих вариантов (вариант А) на рис. 7 показаны удельные прибыли, значения которых являются одним из определяющих факторов как величины максимальной прибыли производителя, так и смещения цены, максимизирующей прибыль производителя.

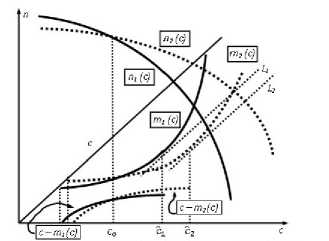
Рис. 7. Вариант А соотношения значений c_G < С 1 < С 2

Для варианта А можно сразу сказать, что получается, с* G [cG; с*]. В этом случае, как это можно увидеть:

если имеют место с* G [c _G ; С1] и

г* = г і (c l = (с* - тДс*))пі(Д) < (с* - т * (с 1 ))п 2 (с 1 ) 6 г * .

Из этого следует, что при выполнении указанных условий производителю выгоден переход от пі к п*. Возможно, что ему придется увеличить объем выпуска, причем может оказаться, что это увеличение объема выпуска произойдет при увеличении (!) цены, см. рис. 7.

Если же только что указанные условия не выполняются, то изменения будут определяться конкретными зависимостями всех величин от цены.

Варианту В отвечает рис. 8.

Для этого варианта сразу можно сказать следующее. В первоначальном состоянии имело место с* < сі < с_с. Для нового состояния и значений цен можно повторить рассуждения, которые приводят к результату (1): все значения г* (с) <  г*.

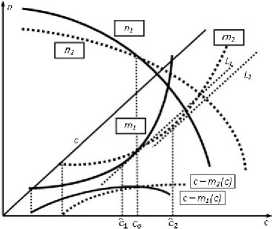
Рис. 8. Соотношение c_G, с1, с ₂

Так как при с = c_G имеем r2(c_G) = гфс^ < гі(с*) = г*, то получается, что после изменения спроса возможность увеличить прибыль производителя по сравнению с первоначальной может быть только тогда, когда соответствующая цена с Е (c _G ; с^). В любом случае при реализации варианта В стремление производителя максимизировать свою прибыль повлечет уменьшение соответствующего объема выпуска.

Наконец, рассмотрим вариант С, для чего воспользуемся рис. 9.

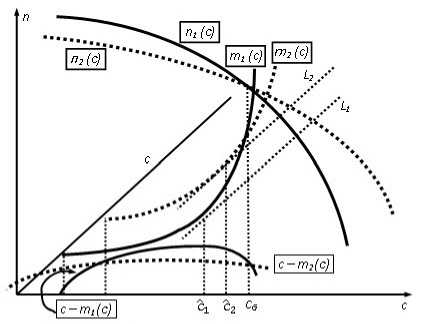
Рис. 9. Возможное соотношение c_G, С1 и С 2

В данном случае сразу видно, что при соответствующих с < c _G имеет место соотношение г₂< гу (так как пу > п₂, с — mi >  с — m2). Значит, для указанного диапазона цен заведомо г* < г*. Этот результат, на самом деле, будет иметь место вообще для всех значений цен, так как при с >  с_(} и удельная прибыль, и объем выпуска меньше, чем в исходном состоянии при максимальной прибыли производителя. Объем выпуска, соответствующий максимуму прибыли производителя в новом состоянии, также будет меньше такового для исходного состояния. Смещение цены, максимизирующей прибыль, будет зависеть от конкретных параметров начального и конечного состояний.

3.    Последствия одновременного изменения спроса бедных и богатых при изменяющейся зависимости т(п)

Последствия изменений спроса бедных и богатых в случае одновременного увеличения себестоимости т(п) представлены на рис. 10.

На этом рисунке обращает на себя внимание то, чем он принципиально отличается от рисунков предыдущего пункта (когда зависимость себестоимости от объема выпуска не менялась при изменении спроса). На тех рисунках равенства спросов в начальном и конечном состояниях и равенства себестоимостей (как функций от цены) были при одной и той же цене с^ На данном рисунке равенство спроса в разных ситуациях и равенство себестоимости (как функции от цены) имеют место при разных ценах, соответственно при

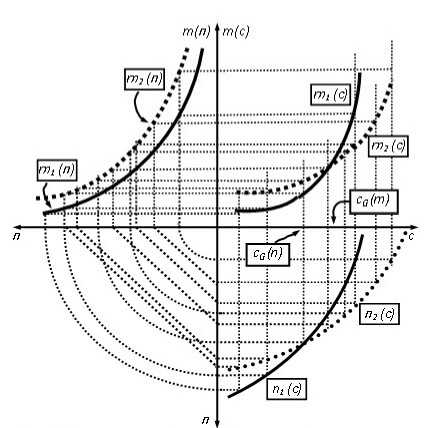
Рис. 10. Изменение спроса, бедных, богатых и себестоимости cG(n) и cG(m), см. рисунок. На рис. 10 видно соотношение этих цен: cG(n) < cG(m). Ответ на. вопрос, является ли такой результат обязательным, содержится в утверждении У.1.

У.1. Если падение спроса бедных происходит одновременно с ростом спроса богатых и ростом себестоимости (как функции объема выпуска), то будет иметь место c_G(n) <  c _G (m).

Доказательство У.1. Пусть n_G(c_G(n)) — значение объема выпуска, отвечающее цене c _G (n). Поскольку считается, что при всех объемах выпуска m₂(n) > m i (n), получаем, что m₂(n _G (c _G (n))) > m_i(n _G (c _G (n))). Каждое из этих значений отвечает одной и той же цене c _G (n ), которой соответствует выпуск n _G (c _G (п)). В силу этого можно записать, что при цене c_G(n): m 2 (c G (n)) > mi (c g (i)).

Зависимости mi(c) и m2 (с) — строго монотонно возрастающие непрерывные функции. При малых значениях цен mi (c) <  m 2 (c), это видно и по только что полученному соотношению между значениями m2(c_G(n)) > mi(c_G(n)). Но m i (c) быстр ее, чем m 2 (c), достигает своих предельно больших значений. Это связано с тем, что минимальные значения пДс) соответствуют меньшим значениям цены в отличие от П2(с). Из этого следует, что m i (c) растет быстрее, чем m 2 (c), при всех значениях цены. Значит, при каком-то значении цены c _G (m) себестоимости в рассматриваемых двух случаях должны оказаться равными. При цене c_G(r) еще было m₂(c_G(n)) >  m_i (c_G(n)), значит, c_G(r) <  c _G (m) Что и требовалось доказать.

Теоретически, возможно 4! вариантов соотношения ключевых величин (c_G(n), c _G (m), ci, C2). Но из-за невозможности соотношения c _G (m) < c _G (n), см. У.1, сразу выпадает половина вариантов перестановки, поэтому остается только 12 вариантов:

• 1.    c_i< c₂< c_G(n) < c_G(m).

• 2.    C2 < ci < cg(ti)< cG(m).

• 3.    c_G(r) < C < c₂< c_G(m).

• 4.    c_G(r) < c₂< C < c_G(m).

• 5.    c_G(r) < c_G(m) < C < C₂.

• 6.    c_G(n) < c_G(m) < c₂< c1.

• 7.    ci < cg(ti)< C2 < c_G(m).

• 8-    C₂< c_G(r) < c_i< c_G(m).

• 9.    cg(ti)< ci < cG(m) < C2.

• 10.    c_G(ri) < c₂< c_G(m) < c_i.

• 11.    c_i< c_G(ri) < c_G(m) < C₂.

• 12.    C2 < cg(ti)< cG(m) < ci.

4.    Варианты соотношения величин при максимальной прибыли

На рис. 11 и 12 показаны два возможных варианта соотношения ключевых величин (№ 4 и № 9 соответственно).

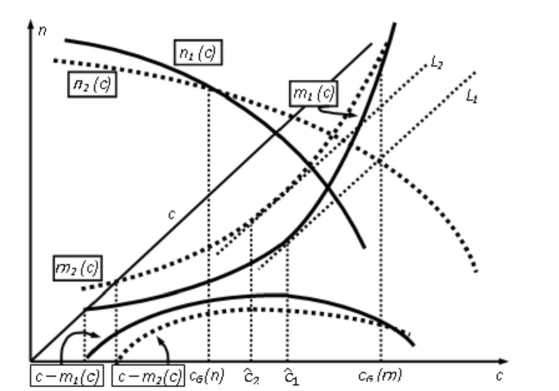
Рис. 11. Соотношение c_G (п) < с₂< щ <  c_G(т)

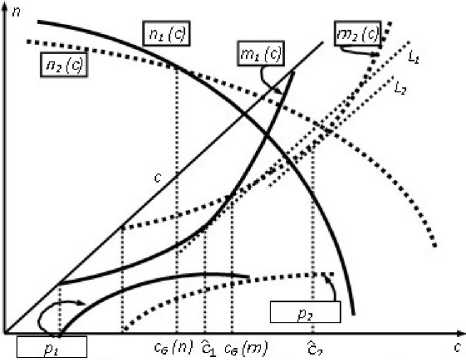
Рис. 12. Соотношение c_G (п) < С 1 < c_G(m) < с₂

Что-либо конкретное о соотношениях ключевых величин и величин, максимизирующих прибыль производителя в обоих случаях, можно сказать, только зная в каждом из случаев зависимости спроса от цены и себестоимости от объема производства. Но на качественном уровне определенные результаты можно получить сразу. Польза такого анализа в том, что можно увидеть основные тенденции и закономерности функционирования производителя.

Далее операция дифференцирования по цене c обозначена штрихом (благо мы имеем дело с простой зависимостью всех переменных от цены).

Воспользуемся также тем, что прибыль представима в виде г = (c — m(c))п = рп = = cп — тп. В последней разности cп — общий доход производителя, пт — общие затраты. Эти представления позволяют получить цену, с*, доставляющую максимум прибыли. Для этого должно выполняться необходимое условие экстремума:

Г = (рп)’ = (cп)’ — (тп)’ = 0. (2)

Цена c * соответствует максимуму дохода производителя, т.е. случаю (cп)’ = 0. Важно, что при зависимости себестоимости от объема выпуска между ценами и могут быть противоположные соотношения превосходства. Приведенные соображения удобно использовать для анализа ситуации, когда себестоимость зависит от объема выпуска. Возможны следующие варианты.

ПЕРВЫЙ ВАРИАНТ. Пусть c * <  с* и при быль г = рп еще растет, т.е. (рп)’ > 0. Из соотношений c = т + р, (cп)^, = (тп)’ + (рп) при цене получаем: (тп)’ < 0, т.е. расходы на производство при цене c * уже падают, а потому максимум затрат достигается при цене

(обозначим эту цену с_т) меньшей, чем с*. Как уже было сказано, также имеют место соотношения, см. [2]: с * < С. В итоге между перечисленными ценами получается соотношение: с_т< с * < с* < С.

Если собрать воедино результаты проведенного анализа в виде общей иллюстрации, то получится рис. 13.

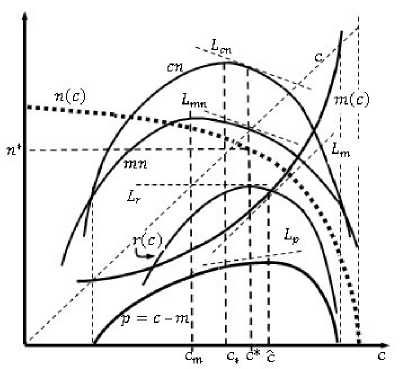
Рис. 13. Геометрическое представление зависимостей и соотношений в первом варианте

На этом и следующем рисунках использованы дополнительные обозначения для новых элементов:

сп — график зависимости дохода как функции цены;

тп — график зависимости затрат как функция цены;

L_cn ~ касательная к графику сп в точке этого графика при цене с*;

L_mn — касательная к графику тп в точке этого графика при цене с*;

L_m — касательна я к графику т(с) при так ой цене с, при которой эта касательная к данному графику параллельна графику цены с;

Lp — касательная к графику р(с) = с — т(с) в точке этого графика при цене с*;

L_T — касательн ая к графику г (с) в точке этого гр афика при цене с*.

Графики L_cn и L_mn параллельны друг другу при цене с*, так как в силу условия (2) они имеют одинаковые угловые коэффициенты при этой цене.

ВТОРОЙ ВАРИАНТ. Пусть при цене с = с * прибыль г = р_п уже надает, т.е. (рп) <  0. В таком случае с * < с* и из соотношения (2) при цене с * полу чаем: (сп) = (рп)’ + (тп) = 0, значит, имеет место (тп) >  0. Таким образом, в данном случае расходы на производство при цене с * еще растут, а потому максимум затрат достигается при цене с_т большей, чем с*. По-прежнему должно и меть место соотношение с* <  с.

Важно, что значение цены с * не может находиться (как и в предыдущем варианте) между значениями с _т и с * при неравенстве этих цен и любом их соотношении. Это связано с тем, что в интервале между указанными ценами производные (тп)’ и (сп)’ имеют разные знаки, а потому невозможно выполнение необходимого условия (2).

В итоге между перечисленными ценами, в отличие от случая постоянной себестоимости, получаются соотношения: с * < с* < с_т, с* < с. Значит, графики L_cn и L_mra, параллельные ДРУ^Г ДРУ^ГУ при цене с*, находятся на восходящих ветвях графиков сп и ст, см. рис. 14, на котором использованы те же обозначения, что и для предыдущего рисунка.

ТРЕТИЙ ВАРИАНТ. В этом варианте имеет место соотношение: с _т = с* = с* <  с. Соответствующий рисунок получается понятным образом по аналогии с двумя предыдущими.

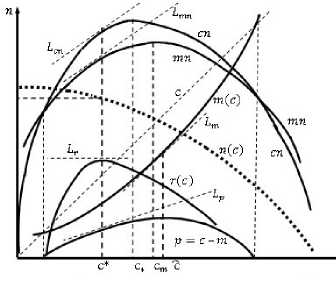
Рис. 14. Геометрическое представление зависимостей и соотношений во втором варианте

5.    Заключение

Как и в предыдущей публикации, все ситуации рассматривались в условиях полной определенности и известности всех исходных данных. Цель такого упрощенного рассмотрения в том, чтобы получить результаты, которые могут представлять определенный интерес, поскольку дают качественное представление о том, что происходит и оказывается возможным для производителя при его функционировании.