Геометрическое программирование и задачи проектирования
Автор: Бухвалова Вера Вацлавовна, Филатов Антон Романович
Журнал: Образовательные технологии и общество @journal-ifets
Статья в выпуске: 1 т.20, 2017 года.
Бесплатный доступ
Геометрическое программирование (ГП) гораздо реже включается в математические курсы для инженерных специальностей, чем линейное и выпуклое программирования. Однако в последнее десятилетие ситуация изменилась. Это связано с тем, что были разработаны эффективные методы решения задач ГП и доказана сводимость довольно широкого класса нелинейных задач оптимизации к задачам ГП. В статье описаны два класса задач, для которых В.В. Бухваловой и её учениками была предложена схема их сведения к задачам ГП: экономические задачи с функциями с постоянной эластичностью замены и задача выбора оптимальных параметров балки, у которой помимо напряжений сжатия/растяжения присутствуют напряжение сдвига. Для популяризации идей и методов ГП в рамках Национального Открытого Университета «ИНТУИТ» был создан интернет-курс «Введение в геометрическое программирование», который успешно используется уже на протяжении 7 лет. Рассказ о структуре этого курса, опыте его использования в учебном процессе и планах его усовершенствования на базе системы MyOpenMath - вторая тема этой статьи.
Геометрическое программирование, интернет-курс, система myopenmath
Короткий адрес: https://sciup.org/14062758
IDR: 14062758
Текст научной статьи Геометрическое программирование и задачи проектирования
Геометрическое программирование (ГП) - сравнительно новый подход к решению нелинейных задач оптимизации специальной структуры, который редко в должном объёме включается в математические курсы для инженерных специальностей. Хотя история этого направления началась с применения его именно к задачам инженерного проектирования. Первая монография по ГП ( [24] ), автором которой является родоначальник этого направления К. Зенер, называется «Engineering Design by Geometric Programming». Последнее десятилетие были разработаны эффективные методы решения задач ГП и методы сведения довольно широкого класса нелинейных задач оптимизации к задачам ГП. Расширился и список областей исследований, в которых применяется ГП. С этими результатами можно ознакомиться в работах, приведённых в списке литературы ( [11, 12, 13, 14, 18, 21] ).
Статья имеет следующую структуру. Раздел 2 посвящён краткому обзору основных постановок задач ГП. В разделе 3 на примере экономической задачи оптимизации выпуска с целевой функцией с постоянной эластичностью замены приводится схема её сведения к задаче ГП. Задача выбора оптимальных параметров балки, у которой помимо напряжений сжатия/растяжения присутствуют напряжения сдвига, обсуждается в разделе 4. Приведён пример сведения частного случая этой задачи к задаче ГП. В разделе 5 рассказано об интернет-курсе «Введение в геометрическое программирование», который успешно используется уже 7 лет в рамках Национального Открытого Университета «ИНТУИТ».
Геометрическое программирование
История геометрического программирования началась в 1961 г., когда К. Зенер опубликовал статью [23] , в которой привел примеры задач инженерного проектирования, которые можно сформулировать как задачи оптимизации обобщённых полиномов, и доказал, что оптимальное решение этих задач является решением специальной системы линейных уравнений. В 1967 году Даффин, Питерсон и Зенер опубликовали монографию [6] , в которой впервые ввели термин геометрическое программирование для обозначения специального класса задач нелинейной оптимизации. Введение этого термина обусловлено тем, что в ранних исследованиях по ГП широко использовалось геометрическое неравенство Коши и его обобщения. Все имеющиеся на настоящий момент подходы к решению задач ГП базируется на теории двойственности, которая впервые была описана в работе Даффина и Питерсона [15] .
В классической постановке задача ГП заключается в минимизации некоторого позинома при ограничениях, согласно которым значения других позиномов не должны превышать единицы:
Задача A
S0 (х) ^ min при ограничениях дк(х) < 1, к = 1, .,р,
X j > 0, j = 1,..., m, где т 9 к (х) = ^ с^, ie[k] j=1
к = 0, ., р, с( > 0.
Функции дк (к = 0, ., р) - это обобщённые полиномы, состоящие из суммы одночленов из индексного множества [/с]. Каждый одночлен внутри полинома является произведением строго положительного коэффициента С/ и переменных х, с показателями степени а/,. Эти показатели степени (в отличие от обычного полинома) могут быть любыми вещественными числами. Такие полиномы называются позиномами. Область определения позинома, поскольку возможен дробный и/или отрицательный показатель, ограничена строго положительными вещественными числами.
Обозначим через п общее число одночленов, входящих в р + 1 позином. Тогда индексное множество I = [1,..., п] нумерует их последовательно так, что первый элемент позинома д0 имеет номер 1, а последний элемент позинома др -номер п. Будем обозначать через [к] индексное подмножество, соответствующее позиному gk:
I = [1] и [2] и ... и [р], [к] П [Z] = 0 при [к] * [I].
Двойственная задача к задаче A (задача B ) имеет нелинейную целевую функцию и линейные ограничения:
Задача B
v(l, d) = ^^(c//d/^^П^) ^ max при ограничениях
Zie[k] dt = Ik, к = 0,..., р,
l0 = 1 (нормальность), £”=1diai;- = lk, j = 1, ..., m (ортогональность), di,lk > 0, к = 0, _,р, i = 1, _,п.
Методы решения задач ГП являются либо прямыми – непосредственно решающими нелинейную прямую задачу A , либо двойственными – решающими эквивалентную двойственную задачу B . Заметим, что сначала были разработаны именно двойственные методы. Эти методы условно можно разбить на две группы. К первой группе относятся методы, в которых используются необходимые условия Куна-Таккера и достаточные условия оптимальности для двойственной позиномиальной задачи. Методы из второй группы используют линейность ограничений двойственной задачи и возможность её переформулировки, при которой число переменных будет равно размерности множества всех решений в линейных ограничениях. Эта переформулировка называется редуцированной двойственной задачей и была впервые предложена в [15] . В двойственных методах часто используется линеаризация, впервые описанная Даффином в [16] .
Класс задач, для решения которых можно применять методы ГП, можно существенно расширить: в [6] показано, что любая корректно поставленная алгебраическая задача может быть преобразована в эквивалентную задачу со знакопеременными полиномами, которая затем при помощи преобразований, описанных в [17] , преобразуется в эквивалентную позиномиальную задачу. Однако на практике выполнение этих преобразований требует применения различных математических приёмов, что мы продемонстрируем в следующих двух разделах этой статьи.
Функции с постоянной эластичностью замены
Традиционным подходом к решению задачи максимизации производственной функции с постоянным коэффициентом эластичности замещения при ограничении на ресурс является построение линейной аппроксимации целевой функции, после которой происходит применение методов линейного программирования [19]. В работе [3] впервые было показано, что эта задача может быть преобразована в эквивалентную задачу ГП. Доказанный факт верен и для многих других функций с постоянной эластичностью замены.
Предполагается, что рассматривается следующая задача:
Задача E
U(К, L) = (аКр + (1 - a)Lp)1/p ^ max при ограничении
ркК + pLL < w, где
U(К, L) - объём производимой продукции,
К - капитал, К > 0,
L - труд, L > 0,
0 < а < 1, рЕ ]-^; 1], рк - стоимость единицы капитала К, рк > 0, pL - стоимость единицы труда L, pL > 0, w - совокупный бюджет, w > 0.
Имеются различные примеры применения этой модели для анализа реальных экономических сюжетов: задача о вторичной занятости, стратегия импортёра для повышения эффективности отрасли, поведении домашних хозяйств.
Под эластичностью в экономике понимают меру чувствительности одной переменной (в рассматриваемой модели - капитала К) к изменению другой (в рассматриваемом модели - труда L) в предположении неизменности значения некоторой функции (в рассматриваемом модели - объём производства U). Коэффициент эластичности о показывает, на сколько процентов изменится первый показатель при изменении второго на 1%. Для целевой функции задачи Е коэффициент эластичности о постоянен и верна формула (см., например, [8] ):
о = 1-р, р Е ]-ю; 0[ U ]0; 1[.
Рассмотрим сначала задачу E при 0 < р < 1. Введём дополнительную переменную То > 0 и заменим целевую функцию минимизацией позинома:
Т-1/р ^ min при ограничении
аКр + (1 - a)Lp > То.
Разделим обе части этого ограничения на То (> 0):
аК^1 + (1 - a)LpT0-1 > 1. (1)
Получили обратное ограничение задачи ГП, которое преобразуем в прямое ограничение, используя лемму из [6] . Согласно этой лемме, выполняется неравенство:
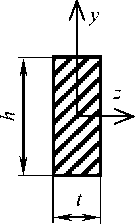
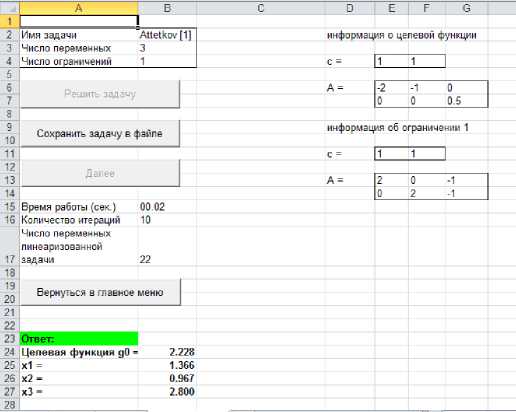
1/g(t) N g(t) = ^u(t), Ui(t) = cit^t^2... t^m i=i и положительных весов /?1,., PN, таких что Е/=1/?1 = 1, соответствующим гармонически обратным называется позином: N 1 И g (t; P) / z,y 4-» ui(t) i=i Возьмём положительные P1 и P2, такие что P1 + р2 = 1, получим для ограничения (1): — КрТ-1 + -2— LpT-1 < 1. а 1 - а Рассмотрим бюджетное ограничение задачи E. Разделим обе его части на w (> 0): w 1ркК + w 1pL[< 1. Таким образом, мы получили задачу ГП (р = 2, т = 3): Т-1/р ^ min при ограничениях — КрТ-1 + -^—TpTQ1 < 1, а 1 — а 4. Статически определимая балка Преобразование задачи E при р< 0 аналогичное, но существенно проще: не потребуется преобразовывать обратное ограничение. В результате получим следующую задачу ГП (р = 2, т = 3): Т0-1/р ^ min при ограничениях аКрТ0-1 + (1 — а)[рТ0-1< 1, w-1pKK + w-1pL[< 1. Аналогичные преобразования могут быть проведены и с другими функциями, имеющими постоянный коэффициент эластичности замены. Уже в первой монографии, посвященной ГП [7], К. Зенер рассматривает задачу минимизации веса арки в гражданском строительстве и приводит её сведение к задаче ГП. При этом он отмечает, что «система напряжений арки чрезвычайно проста, . .она находится под напряжением чистого сжатия». Из теории известно, что это линейное напряжённое состояние, которое описывается достаточно простым уравнением. В развитие этих идей авторы рассматривают классическую задачу плоского напряжённого состояния, изучаемую в курсе сопротивления материалов: свободно опёртая однородная металлическая балка AB длиной i нагружена равномерно распределённой поперечной нагрузкой q(рис. 1). Балка имеет прямоугольный профиль шириной t и высотой h(рис. 2). Требуется найти балку минимальной массы М, удовлетворяющую условиям прочности (весом конструкции по сравнению с нагрузкой можно пренебречь): Задача S M(t, h) = pith ^ min при ограничении ^iv < [a], где р = const - плотность материала балки, р > 0; aIV- эквивалентное напряжение в балке, вычисленное по IV (энергетической) теории прочности: aiv ^ ax + 3ТхУ [a] - допускаемое напряжение. При этом компоненты ох и тху тензора напряжений вычисляются согласно теории Тимошенко [9]. Вопрос устойчивости стенки балки выносится за пределы рассмотрения. Рис. 1. Конструктивная схема закрепления балки и её нагружения, а также связанная с ней система координат Рис. 2. Профиль поперечного сечения балки и обозначения его размеров Очевидно, что минимизация массы М эквивалентна минимизации площади А профиля балки: g0(t,h) = А = th ^ min, которая по своему виду является позиномом. Для авторов задача имеет чисто математический интерес, поэтому помимо естественных ограничений t > 0 и h > 0 на размеры профиля также накладываются удобные, с точки зрения вычислений, ограничения: t< I, h (Qi(t, h) = l-1t < 1, tg2 (t, h) = l-1h < 1. Остаётся лишь канонически записать прочностное ограничение. Для этого сначала необходимо при фиксированных размерах профиля балки определить точки локальных максимумов эквивалентного напряжения ctiv. Прежде перехода к поиску этих точек отметим, что все выкладки удобно производить с использованием внутренней системы координат (f, д, £) балки: f — x/l - 1/2, д — y/h, < — z/t. В этих обозначениях нормальные и касательные напряжения соответственно принимают вид , ч ql2h 1а z ql2hh 1 "'(f,g) = - "2/7(4 - fp,A$,д) = - -^;те(,4 -д2), th3 где /z = — - момент инерции профиля. Тогда ql2h 1 \2 h\2 1 2 °iv(f,g)=M(4-f2) д2+3(т) f2(4-д2). Заметим, что O"IVявляется чётной функцией по обоим аргументам, поэтому достаточно найти точки локальных максимумов только внутри квадрата [0,1/2]2. Применяя стандартную технику дифференцирования и поиска стационарных точек с последующим сравнением значений функции в найденных точках со значениями функции на границе области определения, приходим к выводу, что эквивалентное напряжение достигает своих локальных максимумов в точках (0,1/2) и (1/2,0), а также в симметричных им точках (0, — 1/2) и (— 1/2,0): 3 ql2 3^3 ql aiv(0,1/2) = aiv(0, — 1/2) = 4 t-, av(1/2,0) = aiv(—1/2,0) = — tL которые соответствуют наибольшим нормальному и касательному напряжениям (тут стоит сказать, что у наибольшего касательного напряжения появляется коэффициент V3). Полученная система прочностных ограничений записывается в виде позиномов: 3 ql2 83(t, У=4Йt A < 1 ^Ct ^) =34^ t-1^-1 < 1. Введём обозначения: Co:= 1-1, q : = 3£, c2:= . 0 1 4 [ст ] 2 4 [ст] Учитывая эти обозначения, система ограничений перепишется в виде: Cot < 1, Coh < 1, C1t-1^-2 < 1, c2t-1^-1 < 1, Приведём вектор коэффициентов и матрицу экспонент для сформулированной задачи ГП: l Л ( 15,2 /110 —1 —1 \T c — {1, Co, Co, C1, C2}, Л = (azy)1,1 = 0 1 —2 - 1 ) • Для решения этой задачи воспользуемся двойственностью. Поскольку прямая задача имеет пять мономов, двойственная функция v имеет пять переменных d = (dn ^2, ^з, ^4, ds): «о - Q" (Г (Г CL:' / . Г" * W** — Запишем условия нормальности и ортогональности с учётом неотрицательности двойственных переменных: ( d1 - 1, j d1 + d2 — d4 — dg — 0, I d1 + d3 — 2d4 — dg — 0; dz > 0, i — 1,^,5. Решение полученной системы уравнений можно представить в виде двухпараметрического семейства: d — (1, d2, d3, d3 — d2,1 + 2d2 — d3), 0 < d2 < d3 < 1 + 2d2, следовательно, По условию t < l ^ q/l < q/t — p, где p - среднее давление, действующее на верхнюю поверхность балки, причём на практикеp ^ [a], откуда -— « 1. 4 l[a] В такой ситуации очевидно, что двойственная функция v максимальна при d2— d3— 0. Поэтому минимальная площадь Л* профиля балки равна 3V3 ql А* = g0(t*, h*) = v(1,0,0,0,1) = —[О]. На последнем этапе запишем условие существования оптимального решения: t*h* 3V3 ql которое совместно с ограничением д3 решений _Тй приводит к однопараметрическому семейству h* = а^, t* = 19—, 1 < а < V3. V3 а 4 [а] В завершение следует отметить, что более корректными, с точки зрения применимости балочной теории, являются геометрические ограничения t < l/10, h< l/10, приводящие нас к двойственной функции вида -)=4 '41 9 , 1 которая в случае — < — максимальна уже при 4 [а]’ (d2,d3) = (0,1). Тогда мы получим решение А* _ 30 q£ h* <— t* = 300 Q 4 [а], — 10, 4 [а], которое находится на границе геометрических ограничений. А в случае yj-y > у|у задача решений не имеет, так как требуется хотя бы один размер профиля, превосходящий 1/10. Интернет-курс по ГП Для популяризации идей и методов ГП под руководством В.В. Бухваловой в рамках Национального Открытого Университета «ИНТУИТ» был разработан интернет-курс по геометрическому программированию «Введение в геометрическое программирование», который успешно используется уже на протяжении 7 лет [4, 5,25]. За это время на курс записалось около 500 слушателей. Курс состоит из семи лекций, в которых рассмотрены следующие темы: неравенство Коши и его обобщения, задачи ГП без ограничений и с ограничениями, теория двойственности, связь теории ГП с теориями линейного и выпуклого программирования, методы преобразования некоторых классов задач оптимизации в задачи ГП. Излагаемая теория демонстрируется на многочисленных примерах. Там, где это возможно, описываются методы решения задач ГП с использованием средств MS Excel. Специфика интернет-курса нашла своё отражение в двух деталях. Во-первых, для каждой лекции разработаны практические задания в виде тестов и упражнений, позволяющие закрепить материал лекции. Во-вторых, для задач ГП, решение которых требует применение специальных методов, предлагается использовать созданный авторами пакет GeomProg. Установка этого пакета предельно проста, так как он создан как приложение к MS Excel (язык программирования VBA). Описанию пакета GeomProg посвящена последняя лекция курса. В существующей версии курса при процессе сдачи экзамена слушателю предлагаются задачи из фиксированного набора, подготовленного авторами курса. Для решения задач ГП в пакете GeomProg реализован двойственный метод, предложенный в [22]. Суть этого метода состоит в том, что исходной задаче ГП с ограничениями в стандартной постановке ставится в соответствие пара эквивалентных задач (прямая и двойственная), которые являются задачами обобщённого линейного программирования. Такая замена позволяет устранить вычислительные трудности, обычно связанные с двойственностью – наличие неактивных ограничений и недифференцируемость. Перечислим основные возможности пакета: • решение задачи ГП с ограничениями; • поддержка русского и английского языков; • поддержка стандартных способов ввода-вывода, сохранения данных и • формирование отчёта по итерациям; • формирование листа с отчётом о решении задачи; • получение информации о времени решения задачи и количестве итераций. К пакету GeomProg прилагается банк задач ГП, состоящий на настоящий момент из 74 задач, отобранных из 29 источников. Для каждой задачи, включенной в банк, указываются полные библиографические данные её источника, условие задачи и решение. Поэтому банк можно использовать как для составления дополнительных заданий, так и для тестирования вновь создаваемого программного обеспечения. В качестве примера на рис. 3 приведён фрагмент листа с условиями задачи Attetkov [1] из банка задач. Полученное решение этой же задачи приведено на рис. 4. А В C О Е F GH 1 _______________________________________________________________________ 2 Имя задачи Attetkov [1] информация о целевой функции 3 I Число переменных 3 ____________ 4 Число ограничений______1__________ с = |1 1| 7 Решив, задачу | Е 9 | „ л - I информация об ограничении 1 ^ Сохранить задачу в файле т г п г 33 С= |1 1| 12 _________________________ 14 | 2-1 ЗЕ ЗЕ ЗЕ 19 о I 2Q Вернуться в главное меню Рис. 3. Фрагмент листа с данными задачи Attetkov [1] Рис. 4. Фрагмент листа с решением задачи Attetkov [1] Наряду с продолжением расширения банка задач ГП, авторы планируют создание программы-генератора случайных задач ГП с заданными свойствами. Именно такой подход является современным при создании интернет-курсов. В качестве платформы предполагается использовать систему MyOpenMath [2].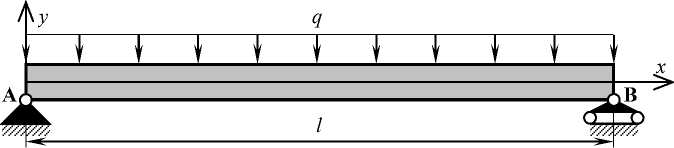
9 q 1 V3 3V3 ql
V(d) (4 l[aj У 4 [a]'
9 q
Список литературы Геометрическое программирование и задачи проектирования
- Бекишев Г.А., Кратко М.И. Элементарное введение в геометрического программирование -М.: Наука, 1980.
- Бухвалова В.А., Бухвалова В.В. MyOpenMath: от генерации задач до полной сетевой поддержки курсов//Компьютерные инструменты в образовании -2015. № 2. -С. 49-62.
- Бухвалова В.В., Рогульская А.С. Расширение области применимости методов геометрического программирования//Обозрение прикладной и промышленной математики -2008. Т. 15, выпуск 2. -С. 270-273.
- Бухвалова В.В., Рогульская А.С. О создании интернет-курса «Введение в геометрическое программирование»//Обозрение прикладной и промышленной математики -2009. Т. 16, выпуск 3. -С. 457-458.
- Бухвалова В.В., Рогульская А.С. Введение в геометрическое программирование -М.: Интернет-Университет Информационных Технологий -2009.
- Даффин Р., Питерсон Э., Зенер К. Геометрическое программирование -М.: Мир, 1972.
- Зенер К. Геометрическое программирование и техническое проектирование -М.: Мир, 1973.
- Плакунов М.К., Раяцкас Р.П. Производственные функции в экономическом анализе -Вильнюс: Минтис, 1984.
- Тимошенко С.П. Сопротивление материалов -М.: Наука, 1965.
- Филатов А.Р. Применение методов геометрического программирования при оптимизации балочных конструкций: дипломная работа -СПб:. СПбГУ, 2016.
- Boyd S. at al. A Tutorial on Geometric Programming//Optimization and Engineering -2007. Vol. 8, № 1. -P. 67-127.
- Chiang M. Geometric Programming for Communication Systems//Foundations and Trends in Communications and Information Theory -August 2005. Vol. 2, № 1. -P. 1-156.
- Chiang M. at al. Geometric Programming for power control//IEEE Trans. Wireless Communications -2006.
- Creese R. Geometric Programming for Design and Cost Optimization (with Illustrative case study problems and solutions) -Morgan & Claypool Publishers, 2011.
- Duffin R.J., Peterson E.L. Duality theory for geometric programming//SIAM J. Appl. Math. -1966. Vol. 14, № 6. -P. 1307-1349.
- Duffin R.J. Linearizing geometric programs//SIAM Review -1970. Vol. 12 -P. 211-227.
- Duffin R.J. Geometric programming with signomials//J. Optimization Theory and Applic. -1973. Vol. 11 -P. 3-35.
- Hoburg W., Abbeel P. Geometric Programming for Aircraft Design Optimization//AIAA Journal -September 15, 2014.
- Hoff A. The Linear Approximation of the CES Function with n Input Variables//Marine Resource Economics -2004. Vol. 19. -P. 295-306.
- Lange K., Zhou H. MM algorithms for geometric and signomial programming//Math. Program., Ser. A -2014. Vol. 143 -P. 339-356.
- Martins J.R., Lambe A.B. Multidisciplinary Design Optimization: A Survey of Architectures//AIAA Journal -September 2013. Vol. 51, № 9. -P. 2049-2075.
- Rajgopal J., Bricker D.L. Solving Posynomial Geometric Programming Problems via Generalized Linear Programming//Computational Optimization and Applications -2002. Vol. 21. -P. 95-109.
- Zener C. A Mathematical Aid in Optimizing Engineering Design//Proceedings of the National Academy of Science -1961. Vol. 47. -P. 537-539.
- Zener C. Engineering Design by Geometric Programming -NY: John Wiley, 1971.
- Бухвалова В.В., Рогульская А.С. Интернет-курс «Введение в геометрическое программирование»//Национальный Открытый Университет «ИНТУИТ». URL: http://www.intuit.ru/studies/courses/539/395/info (дата обращения 24.12.2016).


