Для конкретной постановки задачи приведем необходимые определения.

Пусть в игре с природой: S = { A , A ,..., A_m } , m >  2 , - множество

(чистых) стратегий A, A2,...,Am игрока A; П,П,...,Пп, n > 2, - состояния природы П;      числа aij, i е I = {1,2,...,m}, j е J = {1,2,...,n} , - выигрыши игрока A

Решение задачи по принятию решений в условиях неопределенности зависит не только от лица, принимающего решение (ЛПР), но и от объективной среды, окружающей решаемую задачу. Во многих случаях подходящей математической моделью таких задач может служить «Игра с природой». Рациональным игроком A в игре с природой является ЛПР, а «природой» П - объективная среда. Природа абсолютно безразлична к ЛПР и, не преследуя в игре никакой цели, в любой момент случайным образом принимает одно из своих состояний. ЛПР, будучи рациональным игроком, стремится из возможных стратегий выбрать наиболее эффективную. Для сравнения эффективностей или неэффективностей стратегий ЛПР должен выбрать подходящий, по его мнению, принцип оптимальности. Известны различные принципы оптимальности, например, вы-

в игровой ситуации ( A i , П j ) ; aa_y -матрица выигрышей размера m х n (платежная матрица); в = max{ О , : i g I } , j g J ,- показатель благоприятности состояния П .; r ij = P j - a j , i G I , j G J , - риск в игровой ситуации ( A i , П j ) [2, с. 18-25]; Ц г Ц - матрица рисков.

Критерий Вальда (W- критерий) [1; 2, с. 273-308] определяется следующими компонентами: Wi = min{ ay: j g J}, i g I, -W- показатель эффективности стратегии A; Ws = max{W : i g I} - W- цена игры (в стратегиях множества S ); стратегия A называется  W- оптимальной  (во множестве S), если W = Ws ;   SO(W) - множество W- оптимальных стратегий.

Критерий Вальда является крайне пессимистическим выигрыш-критерием, поскольку ориентирует игрока A на то, что при выборе им любой стратегии A природа будет находиться в наихудшем для него состоянии П j , т.е. выигрыш a_y при состоянии П j (в j - м столбце матрицы ||а_у ||) будет наименьшим среди выигрышей при выбранной стратегии A (в i - й строке матрицы || Ц у ||).

Критерий Сэвиджа (Sav - критерий) [3; 2, с. 308–349] описывается следующими составляющими:   Sav = max{r : j g J}, i g I, - Sav - показатель неэффективности стратегии A; Savs = min{Sav : i g I} -Sav- цена игры (в стратегиях множества S ); стратегия At называется Sav - оптимальной (во множестве S ), если Sav = Savs ; SO(Sav) - множество Sav - оптимальных стратегий.

Критерий Сэвиджа является крайне пессимистическим риск-критерием, поскольку убеждает игрока A в том, что при выборе им любой стратегии A природа будет находиться в наихудшем для него состоянии П j , т.е. риск r ij при состоянии

П j ( в j - м столбце матрицы рисков rv ) будет наибольшим среди рисков при выбранной стратегии A_t (в i - й строке матрицы || r j | I)-

С помощью критерия Сэвиджа осуществляется управление риском, состоящее в выборе стратегии, минимизирующей наибольший риск.

В определении критерия Вальда– Сэвиджа важную роль играет выигрыш-показатель a G [0,1], выражающий степень предпочтения, которое игрок A отдает выигрышам. Выбор игроком A значения выигрыш-показателя a G [0,1] является субъективным и связан с психологическими особенностями игрока A , определяющими его отношение к выигрышам и рискам. Величину (1 — a ) G [0,1] будем считать риск-показателем.

Критерий Вальда-Сэвиджа с выигрыш-показателем a g [0,1] ( ( W - Sav )( a )- критерий) [2, с. 654] определяется следующими понятиями: ( W - Sav )_z( a ) = aW — (1 — a ) Sav - ( W - Sav )( a )- показатель эффективности стратегии A_t , i g I ; ( W - Sav )_s ( a ) = max{( W - Sav )_z : i g I } - ( W - Sav )( a )- цена игры в стратегиях множества S ; стратегия A называется ( W - Sav )( a )- оптимальной, если ( W - Sav )_z (a) = ( W - Sav )_s ( a ) ; S O ^{[( W} " ^{Sav )( a )]} - множество ( W - Sav )( a )- оптимальных стратегий.

При a = 0 , критерий Вальда-Сэвиджа превращается в ( — Sav )- критерий, противоположный критерию Сэвиджа, а при a = 1 , - в критерий Вальда. Нетрудно видеть, что критерии ( — Sav )- критерий и Sav - критерий эквивалентны, т.е. множества оптимальных стратегий по этим критериям совпадают.

Показатель эффективности (W - Sav )(a) стратегии Az является как бы абсолютным взвешенным минимальным выигрышем при этой стратегии, состоящим из взвешенного минимального выигрыша aW при стратегии Az за выче- том взвешенного максимального риска (1 — a)Sav. при этой же стратегии. Поэтому критерий Вальда-Сэвиджа также является крайне пессимистическим, поскольку предполагает, что абсолютный взвешенный выигрыш при любой стратегии A будет не больше взвешенного минимального выигрыша aW,.

Отметим, что в [4, 5] рассматривались другие комбинации критериев Вальда и Сэвиджа.

Стратегию A_t назовем синтезированной критерием Вальда-Сэвиджа с выигрыш-показателем a е (0,1) (короче - ( W - Sav )( а )- синтезированной), если она оптимальна по критерию Вальда-Сэвиджа с выигрыш-показателем а и не оптимальна ни по критерию Вальда, ни по критерию Сэвиджа.

Множество (W-Sav)(а)- синтезированных стратегий обозначим через SS [(W-Sav)(а)] (в этом обозначении надстрочная буква s - первая буква английского synthesized –синтезированная). Оче- видно, имеют место соотношения

SS [( W - Sav )( а )] _ ^ O [( W - Sav )( а )] \ |-^ O ( W ) |J OS ( Sav )] и     S S [( W - Sav )( а )] ^ S O[(W - Sav )( а )]

Если существует стратегия, синтезированная (W -Sav )(а)- критерием, т.е. SS[(W-Sav)(a)] ^ 0, то будем говорить, что критерий Вальда-Сэвиджа с выигрыш -показателем а обладает свойством син- тезирования. В противном случае, т.е. когда SS[(W-Sav)(a)] = 0, критерий Вальда-Сэвиджа с выигрыш-показателем α свойством синтезирования не обладает.

При а = 0 или а = 1 , ( W - Sav )( а )- критерий свойством синтезирования не обладает. При m = 2 ( W - Sav ) а ) критерий ни при каком а е [0,1] не обладает свойством синтезирования.

По определению (W-Sav)(а)- критерия мы можем заключить, что он предназначен для синтезирования крайне высоких предпочтений, отдаваемых игроком A выигрышам (а = 1, W -критерий) и рискам

( а = 0 , Sav -критерий).

Применяя ( W - Sav )( а )- критерий, игрок A надеется в качестве оптимальной получить синтезированную стратегию, а не стратегию, оптимальную по исходным критериям Вальда или Сэвиджа. Проверить существование ( W - Sav )( а )- синтезированных решений для каждого значения а е (0,1) принципиально невозможно, поскольку эти значения составляют бесконечное множество. В связи с этим возникают две проблемы синтезирования критерием Вальда-Сэвиджа:

Р 1 . При каких необходимых и достаточных условиях, критерий Вальда-Сэвиджа ни при каком значении выигрыш-показателя а е [0,1] не обладает свойством синтезирования.

Р 2. При каких необходимых и достаточных условиях существует единственное    значение    выигрыш-показателя а е [0,1], при котором критерий Вальда-Сэвиджа обладает свойством синтезирования; какова формула вычисления этого единственного значения; как при этом найти сами синтезированные стратегии.

Проблема Р 1 решена в [6] в рамках двухкритериальной задачи оптимизации и в [7] - без привлечения двухкритериальной задачи оптимизации в терминах теории игр с природой. В [8] дано геометрическое решение проблемы Р 1 . В [9] анонсированы результаты решения проблемы Р 2 .

В данной работе анонсируются результаты геометрического решения проблемы Р 2 .

Рассмотрим величины

W ( S O ^{( Sav} ) ) = max { W : A е S O ^{( Sav} ) }     и

Sav ( S O ^{( W} ) ) = min{ Sav : A е S O ^{( W} ) } , на основании которых определим следующие множества стратегий:

( s^{o (W} ) ) sav = { a е S O ^{( W} ) : Sav = Sav ( S O^(W ) )} - множество W - оптимальных стратегий

A , показатель неэффективности которых

Sav_t равен Sav ( S O ⁽ W ) ) ;

(S

O ( Sav ) W

= {A e SO(Sav): W = W(S

O(Sav )

)}

- множество Sav - оптимальных стратегий

A , показатель эффективности которых

W равен W ( S O ^{( Sav} ) ) .

Каждая стратегия A e S , i e I , порождает в системе координат Sav oW точку N ( - Sav , W ) с абсциссой ( - Sav )

и ординатой W . Множество всех таких точек обозначим через N , т.е. N = { N , i e I } .

Мы дадим решение проблемы Р 2 в терминах расположения точек N в системе координат Savo W .

Построим в системе координат Sav oW точки

B = (- Sav ( S O ^{( W} ) ), W_s ) ,

C = (-Savs, Ws),

D = (- Sav_s , W ( S O ^{( Sav} ) )) .    (1)

На рис.1 изображены точки B , C , D и символически представлены некоторые точки N .

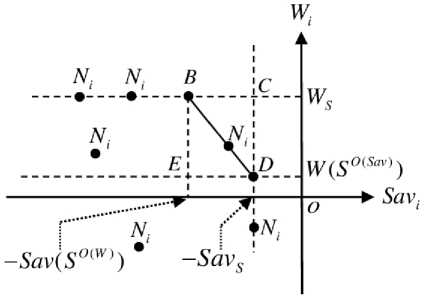
Рис.1. Точки В, С, D, Nj.

Теорема 1. Если число стратегий m >  3 и не существует стратегии, порождающей точку C ( C ^ N ) , то следующие утверждения эквивалентны :

• a )    существует единственное значение выигрыш-показателя

  \WSav)

  
  

  Sav(S°^)-Sav_s

  
  

  Sav(S^w)-Sav_s

  
  

  + W_s-W(S°^

  
  
  
  

при котором критерий Вальда-Сэвиджа обладает свойством синтезирования;

• b )    ни одна из точек множества N не принадлежит внутренности прямоугольного треугольника BCD и во множестве

N существует точка , принадлежащая внутренности гипотенузы BD (см. рис.1);

• c )    множество стратегий, оптимальных по критерию Вальда-Сэвиджа, имеет следующую структуру

  
  

  OKR'&n-X")]

  
  

  ' S^jipu a = 0;

  (S°^wT^PuO№

  j (^f U (^^Г U S^™¹, при a = a_№ (5^отГ\при a_ra

  S⁰⁽ⁿ\ при a = 1.

  
  
  
  

Теорема 2 . Если ни одна из точек множества N не принадлежит внутренности прямоугольного треугольника BCD , то для того чтобы стратегия A была синтезированной , необходимо и достаточно , чтобы порождающая ею точка N принадлежала внутренности гипотенузы BD .

Приложение полученных результатов проиллюстрируем на анализе задачи финансово-экономического содержания, рассмотренной в [10].

Задача . В работе [10] был проведен анализ управления инвестиционной деятельностью структурных подразделений крупной иерархической производственной структуры, предложен подход к выбору приоритетной последовательности структурных подразделений вертикальноинтегрированного холдинга с позиции перспектив централизованного финансирования из общефирменных источников. Полученные результаты были проиллюстрированы на примере АО «Сибирская угольно-энергетическая компания» (СУЭК). В качестве анализирующей модели авторы использовали «Игру с природой», в которой игрок A - АО СУЭК, обладает 14 стратегиями: A , i = 1, 2, ...,14, - финансировать i - е структурное подразделение, где A - ООО «Арктические разработки», A -ООО «Черновские ЦЭММ», A - АО «Разрез Харанорский», A - АО «СУЭК-Кузбасс», A - ООО «Сибнииуглеобогаще-ние», A - АО «Разрез Березовский», A -АО «Разрез Назаровский», A - ООО «Бородинский РМЗ», A - АО «Разрез Тугнуй-ский», A - ООО «Тугнуйская обогатительная фабрика», A - ООО «СУЭК-

Хакасия», A - АО «Разрез Изыхский», A - АО «Ургалуголь», A - АО «Дальт-рансуголь». Роль природы П играют периоды состояний централизованного инвестиционного фонда АО СУЭК, а в качестве конкретных пяти состояний природы были рассмотрены комплексы факторов, определяющих состояния централизованного инвестиционного фонда АО СУЭК так же, как в П - 2014, П - 2015, П - 2016, П - 2017 и П - 2018 годах. Выигрышами в игре были выбраны показатели рентабельности инвестиций из централизованного фонда в предприятия холдинга (отдача на руб. общефирменного капитала), подсчитанные на основании исходных данных из бухгалтерской (финансовой) отчетности АО СУЭК за период с 2014 по 2018 г. В [10] в рамках этой модели была сформирована оптимально-приоритетная очередь стратегий – структурных подразделений, претендующих на финансирование производственных программ и инвестиционных проектов из централизованного общефирменного инвестиционного фонда. При этом в качестве принципа оптимальности был выбран критерий Вальда-Сэвиджа.

Наша цель в условиях этой задачи – выяснить, существует ли единственное значение выигрыш-показателя, при котором критерий Вальда-Сэвиджа обладает свойством синтезирования. Если такое значение существует, то вычислить его и найти синтезированные стратегии, т.е. выявить подразделения АО СУЭК, оптимальные по критерию Вальда-Сэвиджа, но оптимальность которых не сводится к оптимальности по критерию Вальда или по критерию Сэвиджа. Также найти оптимальные не-синтезированные стратегии и соответствующие им подразделения.

Матрица выигрышей имеет следующий вид

П j Ai	П 1	П 2	П 3	П 4	П 5	Wi
A 1	1,373	1,636	0,217	- 1,271	3,781	- 1,271
A 2	6,653	11,979	14,600	1,111	1,579	1,111
A 3	112,000	666,429	1348,571	78,447	72,196	72,196
A 4	71,921	723,201	1407,639	539,298	3293,469	71,921
A 5	5,122	5,168	4,926	4,689	1,616	1,616
A 6	1178,889	416,739	689,333	643,810	506,600	416,739
A 7	625,714	246,324	282,895	262,400	255,645	246,324
A 8	75,455	114,375	33,529	9,821	29,286	9,821
A 9	15,091	953,941	3681,250	2879,375	2165,667	15,091
A 10	1489,167	97,450	12,420	0,991	3,282	0,991
A 11	39,412	566,888	1421,182	1324,886	1159,375	39,412
A 12	2257,000	743,750	895,000	845,625	992,000	743,750
A 13	1,725	3,036	9,616	95,900	978,750	1,725
A 14	347,597	374,648	639,390	529,688	577,841	347,597
р ,	2257,000	953,941	3681,250	2879,375	3293,469	W s = 743,750

В последних добавленных строке и столбце матрицы А проставлены соответственно показатели благоприятности состояний природы в , j = 1,2,3,4,5, и показатели эффективности стратегий W , i = 1,2,...,14, с ценой игры W_s . Матрица

А отличается от матрицы выигрышей, сформированной в [10], незначительными изменениями, сводящимися в основном к округлению элементов матрицы до тысячных.

Матрица рисков, порождаемая матрицей А , выглядит следующим образом:

R =

П j A i	П 1	П 2	П 3	П 4	П 5	Sav
A 1	2255,627	952,305	3681,033	2880,646	3289,688	3681,033
A 2	2250,347	941,962	3666,650	2878,264	3291,890	3666,650
A 3	2145,000	287,512	2332,679	2800,928	3221,273	3221,273
A 4	2185,079	230,740	2273,611	2340,077	0,000	2340,077
A 5	2251,878	948,773	3676,324	2874,686	3291,853	3676,324
A 6	1078,111	537,202	2991,917	2235,565	2786,869	2991,917
A 7	1631,286	707,617	3398,355	2616,975	3037,824	3398,355
A s	2181,545	839,566	3647,721	2869,554	3264,183	3647,721
A 9	2241,909	0,000	0,000	0,000	1127,802	2241,909
A 10	767,8333	856,491	3668,830	2878,384	3290,187	3668,830
A 11	2217,588	387,053	2260,078	1554,489	2134,094	2260,078
A 12	0,000	210,191	2786,250	2033,75	2301,469	2786,250
A 13	2255,275	950,905	3671,634	2783,475	2314,719	3671,634
A 14	1909,403	579,293	3041,860	2349,687	2715,628	3041,860
						Savs = 2241,909

В последнем добавленном столбце матрицы R проставлены показатели неэффективности стратегий Sav , i = 1,2,...,14, с ценой игры Sav_s .

Из матриц А и R заключаем соответственно, что SO(W) = {A2} и SO(Sav) = {A } . Следовательно, W(SO(Sav)) = 15,091 и Sav(SO(W)) = 2786,250. Таким образом, (SO(Sav))W = SO(Sav) = {A }и (SO(W))Sav = SO(W) = {A2}.

В системе координат Sav oW построим точки:

B (-2786,250; 743,750) , C (-2241,909; 743,750) , D (-2241,909; 15,091) ,

N(-3681,033; -1,271),      N(- 3 6 6 6,6 5     N(- 3 2 2 1,2 7 3

N(-2340,077; 71,921),  N(-3676,324; 1,616),  N(-2991,917; 416,739),

N(-3398,355; 246,324),  N(-3647,721; 9,821),   N(-2241,909; 15,091) = D,

N0 (-3668,830; 0,991),  NX-2260,078; 39,412),  N2(-2786,250; 743,750) = B,

N3 (-3671,634; 1,725),  N4(-3041,860; 347,597) .

Данные точки символически представлены на рисунке 2, но символическое представление не изменяет сути их расположения.

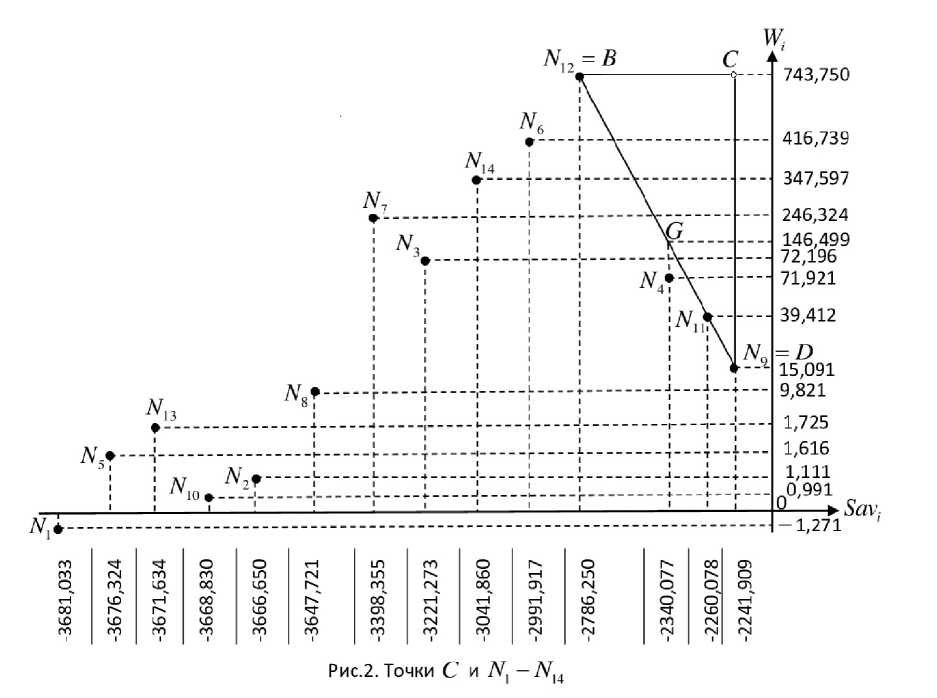
В данной игре число стратегий m = 14 >  3 и ни одна из стратегий не порождает точку C ( C £ N ) .

Поскольку абсциссы точек N , i =1,2,3,5,6,7,8,10,13,14, меньше абсциссы (-2786,250) точки B = N ₂, то точки N , i =1,2,3,5,6,7,8,10,13,14, не принадлежат треугольнику BCD и, следовательно - его внутренности (см. рис.2).

Покажем, что и точка N не принадлежит треугольнику BCD , несмотря на то, что ее абсцисса (-2340,077) больше абсциссы (-2786,250).

Уравнение прямой, проходящей через две точки B(-2786,250; 743,750) и D(-2241,909; 15,091), на которой лежит гипотенуза BD , имеет вид у = -1,338607601x-2985,945428. (4)

Подставляя x = - 2340,077 в уравнение (4), получим ординату у = 146,4994311 точки G ( - 2340,077; 146,499) , лежащей на гипотенузе BD . Так как абсцисса точки

N совпадает с абсциссой точки G , а ее ордината 71,921 меньше ординаты точки G , то точка N не принадлежит треугольнику BCD .

Теперь покажем, что точка N лежит во внутренности гипотенузы BD . Подставим абсциссу x = -2260,078 точки N_n в уравнение гипотенузы (4); получим ординату 39,412, равную ординате точки N . Таким образом, координаты точки N удовлетворяют уравнению (4), т.е. точка N лежит на гипотенузе BD . А поскольку точка N отлична от концов гипотенузы – точек B и D , то точка N лежит во внутренности гипотенузы BD .

Таким образом, выполняются условия теоремы 1 и справедливо утверждение b) этой теоремы. Тогда по теореме 1 справедливо утверждение a), т.е. существует единственное    значение    выигрыш- показателя а = аW-Sav), при котором критерий Вальда-Сэвиджа обладает свойством синтезирования. Это значение найдем по формуле (2):

^IF-Sb-)

2786,250-2241,909

2786,250-2241,909 + 743,750-15,091

= 0,42760487* 0,428.

Используя теорему 2, заключаем, что существует единственная синтезированная стратегия A , т.е. множество синтезированных стратегий одноэлементно: S S [( W-Sav )( а )] _ { д }

Структура множества всех оптимальных стратегий по критерию Вальда-Сэвиджа (синтезированных и несинтези-рованных) по утверждению c ) теоремы 1 определяется формулой (3):

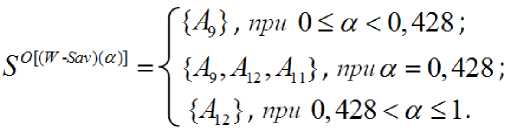
Полученное решение экономически можно проинтерпретировать следующим образом.

Пусть предпочтение руководства АО СУЭК, отдаваемое рентабельности инвестиций из централизованного фонда в предприятия холдинга, характеризуется выигрыш-показателем а в пределах 0 <  а <  0,428 . Следовательно, риск-показатель 1 — а в соответствующих пределах 1 >  а >  0,572 характеризует предпочтение АО СУЭК, отдаваемое риску неполучения наибольшего показателя рентабельности инвестиций. В этом случае критерий Вальда-Сэвиджа в качестве оптимальной рекомендует стратегию A , т.е. в первую очередь финансировать АО «Разрез Тугнуйский». Стратегия A не является синтезированной, поскольку оптимальна по критерию Сэвиджа, и никакое изменение выигрыш-показателя в пределах 0 <  а <  0,428 не приводит к новой стратегии, оптимальной по критерию Вальда-Сэвиджа. Финансируя АО «Разрез Тугнуй-ский», руководство АО СУЭК рискует не получить наибольшую рентабельность инвестиций при каждом состоянии природы не более, чем на 2241,909. Это наименьший риск среди наибольших рисков при финансировании каждого подразделения. А показатель рентабельности инвестиций при финансировании АО «Разрез Тугнуй-ский» составит не менее 15,091.

Если степень предпочтения руководства АО СУЭК, отдаваемое рентабельности инвестиций выражается выигрыш- показателем а в пределах 0,428 < а < 1, то его предпочтение, отдаваемое риску, выражается риск-показателем 1 — а в пределах 1 > а > 0,428. При таких показателях оптимальной по критерию Вальда-Сэвиджа является стратегия A - в первую очередь финансировать АО «Разрез Изых-ский». Стратегия A не является синтезированной, так как оптимальна по критерию Вальда. Финансируя АО «Разрез Изыхский», руководство АО СУЭК получит рентабельность инвестиций не менее 743, 750, а риск составит не более 2786, 250.

Наконец, если а = 0,428 и, следовательно, 1 — а = 0,572, то руководство АО СУЭК в качестве синтезированной по критерию Вальда-Сэвиджа выбирает стратегию A - финансировать в первую очередь ООО «СУЭК-Хакасия». В этом случае рентабельность инвестиций будет не меньше 39,412, что больше 15,091 при стратегии A и меньше, чем 743,750 при стратегии A , а риск не более, чем 2260,078, что больше 2241,909 при стратегии A , и меньше 2786,250 при стратегии A 12 .

Отметим, что представленные результаты применимы к анализу любой задачи по принятию финансово-экономических решений в условиях неопределенности, допускающей в качестве модели игру с природой с синтетическим критерием оптимальности Вальда-Сэвиджа.