Геометрия систем линейных регрессионных уравнений
Автор: Котенко Андрей Петрович, Букаренко Максим Борисович
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Экономика и управление
Статья в выпуске: 6-3 т.15, 2013 года.
Бесплатный доступ
Представлена геометрическая интерпретация метода наименьших квадратов, позволяющая классифицировать возможность идентификации параметров системы линейных регрессионных уравнений. Это даёт возможность в случаях неидентифицируемости или сверхидентифицируемости выдвинуть дополнительные условия, гарантирующие однозначную идентификацию параметров как отдельного уравнения, так и всей системы в целом. Экспоненциальный рост числа вариантов разбиения множества исследуемых факторов на эндогенные и экзогенные усложняет задачу отыскания регрессионных взаимосвязей. В этом случае геометрическая интерпретация системы регрессионных уравнений позволяет целенаправленно подобрать структурную форму модели, обеспечивающую значимость параметров всех уравнений.
Система линейных регрессионных уравнений, структурная форма модели, приведённая форма модели, идентификация параметров модели
Короткий адрес: https://sciup.org/148202637
IDR: 148202637 | УДК: 330.43
Текст научной статьи Геометрия систем линейных регрессионных уравнений
Системы регрессионных уравнений (например, одномоментные системы эконометрических уравнений [1]) – полезный инструмент моделирования взаимосвязанных явлений. Представим геометрическую интерпретацию метода наименьших квадратов для описания идентифицируемости систем линейных регрессионных уравнений.
Рассмотрим систему линейных регрессионных уравнений y1 - aVy + a13y3 +—+alnyn +
+ b n x l + b 12 x 2 + — + b l m — m + A>
— — —— y2 - a21y1+ a23y3 + —+ a2nyn +
< + b21x1 + b22——2 +—+b2 m—m + r2(1)
—* —* —*—*
y n - a n1y1 + a n 2 y 2 + — + a n, n - L y n - 1 +
A b n 1 X ^ + b n 2 X ^ + . + b nm x m ^£ n ,
могут быть нулевыми. Ей соответствует приведённая система
' ~ 1 - ^ 11 X 1 + ^ 12 X 2 + . + ^ 1 m X m , ~ 2 - ^ 21 X + ^ 22 X 2 + . + ^ 2 m X m , ^
,y„ - An 1X1 + An2X2 + — + AnmXm с регрессионными значениями yi -(yi1,~i2, — ,~iN)T G^ N и приведёнными МНК-коэффициентами вij, среди которых могут встретиться незначимые.
Вектора y i - регрессионных значений эндогенных переменных получаются ортогональным проектированием векторов y i наблюдений эндогенных переменных на линейную оболочку L ( X 1 , X 2 , . , X m ) с ^ N векторов экзогенных переменных:
~i - Pr ( y i ; L ( X 1 , X 2 , . , Xm )) g L ( X 1 , x 2 , — , Xm ) , 1 < i < n .
Как правило yi- Ф yt , так как вероятность совпадения y ^ - yi близка к нулю при достаточно большом числе наблюдений N . Приведённые коэффициенты вij являются решениями системы N линейных уравнений с m < N неизвестными
'y1 - A1X11 + A2X21 +— + AmXm 1, y2 - A1X12 + A2X22 +— + AmXm2,
.y iN - A i 1 X 1 N + A i 2 X 2 N + — + A im X mN •
Её ранг r Viе 1,n ^ yi е L(Xi,X2,...,Xm)сЖN , dimL(Xi,X2,...,Xm) = r < m . Без строгой мультиколлинеарности r=m и система (3) имеет единственное решение: ViЕ 1,n ^ Зу Е L(Xi,X^,..,Xm)c^N, dimL(Xi,x2,„,Xm ) = r = m . В дальнейшем предполагаем отсутствие строгой мультиколлинеарности, когда вектора экзогенных переменных xj линейно независимы: dimL(Xi,x2^„,Xm)= m . Этого можно добиться переходом к базису размерности mi Е 1,m оболочки L(Xi,х2,^,Xm), исключив линейно зависимые вектора экзогенных переменных. Заменяя в системе (1) выборочные значения yi эндогенных переменных регрессионными значениями у* из системы (2), получим в линейной оболочке L(X],X2,^,Xm) выборочных значений экзогенных переменных независимые линейные уравнения для идентификации структурных коэффициентов: ~ ~ ~~ yi = a12y2 + a13y3 +—+ ainyn + +bi iXi + bi2X2 +^+bimXm, у у . у .. у . y2 = a2iyi+ a23y3 +—+ a2пУп+ +b2]Xi + b22X2 +...+ b2mXm, Уп = an1y +an 2~2 +-+ an, n-1Уп -1 + +bni Xi + bn2X2 +- • -+bnmmr Из (2), (3), (4) получим систему линейных уравнений для идентификации структурных коэффициентов i-го уравнения Vi E 1 n : m nm y = Z PikXk = Z aij yj + Z bikXk = k=1 j=i; j ^ ik ^m) Z PjkXk + Z bikXk (k =i J n = Z aj j=uj*i ^ n ^ Pii = bii + Z Pj1aij j=i; j * i n Pi2 = bi2+ j=i; j * * n Pim bim + j =i; j * * Для решения СЛАУ (5) рассмотрим вначале подсистему s > 1 уравнений n Pii = bii + Z Pjiaij , j=An*i1 Pi2 = bi2 + Z Pj 2aij , j=i; j * i n _, Pis = bis+Z Pjsaij (6) j=i; j * i с фиксированными структурными коэффициентами bik: например, если экзогенная переменная xk отсутствует в i-ом уравнении, то bik=0 и не требует идентификации. Её решение (ai1,…,ai,i–1,ai,i+1,…,ain) подставим в оставшиеся m–s<m уравнений СЛАУ (5) и доопределим неизвестные структурные коэффициенты (bi,s+1,bi,s+2,…,bim): n bi, s +1 = Pi, s +1 - Z Pjs +1 aij , j=i; j * i n bi, s+2 = Pi, s+2 - Z Pj s +2 aij, j=i; j * i b- = В ••♦, vzm pim n - Z Pjm-i j =i; j * i Обозначим через L(Mi) линейную оболочку объединения Mi := Ni и к* множества векторов регрессионных значений присутствующих в правой части i-го уравнения системы (4) эндогенных переменных Ni:= {уj е ^N : j * i, a*j * o}; (7) 0 < |Nz.|< |MZ.|, Ni| < n< N; и множества векторов выборочных значений экзогенных переменных Ki :={?k E^N : bik * o}; (8) 0 < Ki| < Mi| = Ni| + Ki|, Ki| < m< N ; из правой части этого уравнения: Mi = Ni и Ki c L(Mi )c L(Xi, X2,^, Xm )c^N ,1 < i< n. Идентифицируемость структурных коэффициентов i-го уравнения определяется принадлежностью его левой части у* линейной оболочке L(Mi) векторов правой части (7), (8) и их воз- можной линейной зависимостью. Возможны следующие случаи: 1) если система Mi векторов (7), (8) линейно независима (при этом \Mii\ = |Ni-| + KJ < m< N ) и вектор из левой части уравнения принадлежит её линейной оболочке (т.е. у, е L(М^)), то уравнение точно идентифицируемо и его структурные коэффициенты алгебраически однозначно определяются косвенным МНК (5): ~i = Pr^i, L({~jеNi У {xkеKi }))е L(Mi); 2) если система Mi линейно независима и У g L (М,) , то уравнение сверхидентифициру-емо и структурные коэффициенты статистически однозначно определяются двухшаговым МНК: ~ * Pr(~i, L({~jеNi }u {xkеKi jj)< L(Mi); 3) если система Mi линейно зависима (|Mi| = |Ni| +Ki | < m< N) и уе L(Mi), то уравнение неидентифицируемо и его структурные коэффициенты нельзя (ни алгебраически, ни статистически) однозначно выразить через приведённые, однако их можно алгебраически представить как бесконечное множество решений СЛАУ (5); 4) если система Mi линейно зависима и У^ L(Mi), то уравнение неидентифицируе-мо, однако ортогональную проекцию Pr(у,L(Mi)) можно алгебраически представить как непустое бесконечное множество решений неоднородной системы (5), т.е. структурные коэффициенты этого уравнения статистически неоднозначно представимы через приведённые. Рассмотрим геометрические свойства систем линейных регрессионных уравнений в указанных случаях подробнее. В случае 1) структурные коэффициенты являются решениями СЛАУ с |Mi = |NZ-| + |Ki| -1 неизвестными и N — 2 уравнениями, из которых |Мг-| < N независимы: Уay ~j+ У by j = ~; (9) yjеNi xjеKi yi е L (Mi )- dimL(Mi)= |Mi|, 1 Поскольку вектора уе^N регрессионных значений эндогенных переменных являются линейными комбинациями линейно ^ NN независимых векторов Ху е m , то ранг системы (9) r = |Mi| = NJ+m - KJ ^ ^ |Ni|+ |Ki| = |Ni|+ m - |Ki| « |Ki| = m - |Ki|. В случае 2) векторное уравнение (9) не разрешимо алгебраически, так как его левая часть У aiy уу + У bijXу е L(Mi) в отличие от пра-yj е Ni xj е Ki вой части ~i g L(Mi). Обычным МНК найдём ортогональную проекцию правой части на L(Mi): У aij yj+ У bij x j = Pr (~i ’ L (Mi)). (10) yjеNi xjеKi Система (10) имеет единственное алгебраическое решение. Следовательно, найдено единственное статистическое решение системы (9). В случае 3) перейдём от СЛАУ (9) с линейно зависимой системой Mi к СЛАУ с базисной подсистемой M'c Mi, ‘m' := N' иK', N' c Ni, K^G Ki: У aij ~j+ У bi/'xj = ~i; (11) yjе Ni xjеKi У е L(Mi), i < dim l (m;)=|m;| = |n;|+|k;|< |мг.|, 1 < i< n. Применяя алгоритм решения СЛАУ (5), получим единственное алгебраическое решение системы (11). Тогда система (9) имеет бесконечное множество решений. В случае 4) перейдём от СЛАУ (11) с линейно зависимой системой Mi к СЛАУ с базисной подсистемой M' c Mi, Mi' := N; и K', Ni' c N, K;g Ki: У ajyj+ У bjXj= Pr(У,L(Mi)); (12) yjе Ni xjеKi ~i е L(m;) , i < diml (m;)=|m;| = |n;|+|k;| < |Mi |, 1 < i < n. Здесь ортогональная проекция Pr(у,L(M')) получается обычным МНК. Применяя алгоритм решения СЛАУ (5), получим единственное алгебраическое решение системы (12). Тогда система (9) имеет непустое (и даже бесконечное) множество решений. Представленная геометрическая иллюстрация действия МНК и его модификаций позволяет исследовать идентифицируемость систем линейных регрессионных уравнений в случае дополнительных условий, связывающих структурные коэффициенты.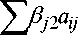
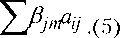
Список литературы Геометрия систем линейных регрессионных уравнений
- Тихомиров Н.П., Дорохина Е.Ю. Эконометрика: учебник. М.: Экзамен, 2003. 512 с


