Геометрооптический расчет оптических элементов для фокусировки в линию в непараксиальном случае

В работах [1-7] рассмотрен расчет функции эйконала из условия фокусировки в произвольную линию. Однако даже в параксиальном приближении аналитический расчет функции эйконала возможен только для случаев фокусировки в простые линии, такие как отрезок, кольцо и т.п. В общем случае произвольной кривой расчет эйконала требует решения нелинейного уравнения для каждой точки апертуры [6, 7].

В работах [6, 7] предложено использовать специальную криволинейную систему координат, значительно упрощающую расчет в параксиальном приближении. В работе [8] предложено использовать другую криволинейную систему координат, позволяющую получить простое аналитическое выражение для функции эйконала в общем, непараксиальном случае. Функция эйконала в [8] зависит от функции a ( £ ), определяющей углы прихода лучей в точки кривой X ( ^ ). Функция a ( £ ) определяет распределение энергии вдоль кривой фокусировки. Для расчета функции a ( £ ) в [8] был использован итерационный метод.

В данной работе расчет функции a ( £ ) сводится к решению обыкновенного дифференциального уравнения первого порядка, разрешенного относительно производной. В качестве примера приведены расчеты функций эйконала из условия фокусировки в отрезок и дугу окружности. По полученным эйконалам рассчитаны преломляющие оптические элементы, формирующие распределения освещенности в виде отрезка и дуги окружности.

1. Функция эйконала в криволинейной системе координат

Для полноты изложения приведем основные результаты, полученные в работе [8]. Рассматривается задача расчета эйконала светового поля из условия преобразования светового пучка с распределением интенсивности I0 (u), где u = (u, v) - декартовы координаты в плоскости фокусатора, в кривую, заданную параметрическим уравнением

X ( ^ ) = ( X О Y О f ), (1)

где £ - натуральный параметр, а f - расстояние от плоскости задания эйконала ( z =0) до плоскости фокусировки ( z = f ).

Будем считать, что выполняется приближение тонкого оптического элемента, в рамках которого расчет оптического элемента, формирующего заданное распределение интенсивности в плоскости фокусировки, сводится к расчету функции эйконала ^ ( u ) в плоскости z =0 [6, 7].

Введем понятие слоя как одномерного множества Г(^) точек (и, v) в плоскости задания эйконала, на правляющих излучение в одну и ту же точку X(^) кривой.

В работе [8] расчет функции эйконала предлагалось проводить в следующей криволинейной системе координат, связанной с лучами:

V a (5)) = -41 + a2© 4f2 +n2 - f a(t)

о 4 1 + a ² ( t )

d t .

Эйконал (3) зависит от функции а ( Ь ), задающей углы раствора конусов лучей, приходящих на линию фокусировки. Функция а ( Ь ) определяет распределение энергии вдоль кривой фокусировки [8].

и ²( Ь , n ) + v ²( Ь , n ) = R ².

2. Формирование заданной линейной плотности энергии вдоль кривой фокусировки

Световой поток, заключенный между слоями Г ( Ь ), Г ( Ь + АЬ ), имеет вид

42©

АФ = АЬ J I о ( ^ , n ) J ( Ь , n )d n ,                  (4)

П 1 (Ь)

где п ₁( Ь ), П ₂( Ь ) - пределы интегрирования по п для слоя Г ( Ь ),

∂ u ∂ v ∂ u ∂ v

J © П) =

∂ξ ∂η ∂η ∂ξ

1 + d O j^ \ f ² +n ² +n ( a ²© + 1 ) K ( Ь )

• -    якобиан преобразования координат,

K = dX ²© d Y © - d X ( Ь ) d Y ²© d ^ ²     d ^      d ^     d ^ ²

• -    кривизна кривой (1).

По построению элемента световой поток АФ , заключенный между слоями Г ( Ь ), Г ( Ь + АЬ ), пере

Подставим (2) в (8) и получим уравнение четвертой степени относительно п:

n ⁴ ( а ²( Ь ) + 1 ) ² +

+n ³ ( 4 ( а ²( Ь ) + 1 ) ( X W( Ь ) - X ( Ь ) Y ‘ ( Ь ) ) ) +

+n ² ( 2 ( а ²( Ь ) + 1 )( R ² - X ²( Ь ) - Y ²( Ь ) -

- а ²( Ь ) f ² ) + 4 а ² ( Ь ) ( X ( Ь ) X ‘ ( Ь ) + Y ( Ь ) Y ‘ ( Ь ) ) 2 +

+ 4 ( X ‘ ( Ь )Y ( Ь ) - X ( Ь ) Y ‘ ( Ь ) ) ² ) +                   (9)

+n ( 4 ( X ‘ ( Ь )Y ( Ь ) - X ( Ь ) Y ‘ ( Ь ) ) х

х ( R ² - X ²( Ь ) - Y ²( Ь ) - а ²( Ь ) f ² ) ) +

+ ( R ² - X²( Ь ) - Y²( Ь ) - а ²( Ь ) f ² ) ² -

- 4 а ² ( Ь ) f ² ( X ( Ь ) X '( Ь ) + Y©Y ‘ ( Ь ) ) ² = 0.

ходит в элемент кривой длины АЬ, , заключенный

между точками Х ( Ь ), Х ( Ь + АЬ ). Соответственно,

Уравнение (9) имеет два действительных решения. Алгоритм решения (9) общеизвестен и приведен, например, в [9].

В случае, когда интенсивность падающего пучка постоянна, 1 ₀ ( u ) = 1 ₀, интегралы в (7) по переменной п вычисляются аналитически. При этом уравнение (7) принимает вид:

световой поток, приходящийся на единицу длины кривой фокусировки, имеет вид

42©

I ( Ь ) = J I о ( Ь , n ) J ( Ь , n )d n .                      (6)

л©

Функция (6) называется линейной плотностью энергии вдоль кривой.

Уравнение (6) позволяет определить функцию а ( Ь ) из условия формирования заданной линейной плотности I ( Ь ) . Действительно, подставив (5) в (6),

da ( Ь ) d ξ

( КЬ)

I 1 0

-

η

-

n ²( а ²( Ь ) + 1)

п=П 2 ( Ь ) Л

/

'[ ⁿ Х⁷^^ + ft _1П |        2          2

У

/

п=П 1 ( Ь ) v

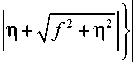
п=П 2 ( Ь ) Л

.

п=П 1 ( Ь ) у

получим для а ( Ь ) следующее дифференциальное уравнение первого порядка, разрешенное относительно производной:

dа(Ь) = dЬ

Рассмотрим случай, когда интенсивность падающего пучка является гауссовской функцией:

I 0 ⁽u© n )) = I 0 • exp

u ²( Ь , n ) 0 2

'^

I(Ь)- J Iо(Ь,n)(1 + n(а2(Ь) +1)K(Ь))dn у

'Л©        ^

J I о ( Ь , n )V f ² +n ²d n

I л©J

где о I - параметр, определяющий ширину гауссовского пучка. Для гауссовского пучка аналитические результаты удается получить при использовании асимптотического метода Лапласа [10]. Используя метод Лапласа для вычисления интеграла в (6), получим

Таким образом, согласно (3), (7), задача фокусировки в кривую с заданной линейной плотностью I ( Ь ) сводится к задаче нахождения функции а ( Ь ) из уравнения (7).

Рассмотрим случай, когда апертура является круглой с радиусом R . Тогда П | ( Ь ), П ₂( Ь ) находятся

из уравнения

г ' и2(Ь,n)Л              f ' S(Ь,n)Л exp--J(Ь, n)dn = exp/ х

У    02   у                 у о2 у хJ(Ь, n)dn =. -   2ПОI    J(Ь, П0(Ь)) х

N s ( Ь , П 0 ( Ь ))

'_ 5(Ъ,П0(Ь)) Л х exp II

У      °,у

где

S ,_ d ²( u ²( ^ , n ))

d n ²     ’

n ₀( ! ) - стационарные точки,

Дифференциальное уравнение (10) принимает вид:

d ( u ²( ! , n )) которые находятся из уравнения --------- _ 0 .

dn

Данное уравнение является уравнением четвертой степени относительно п Таким образом, выражение для линейной плотности (6) принимает вид:

^d a ^{( ! )} d !

n R2

_ — -(n2С!)-^(5)) x

nVf2 +n’ 2

I ( ! ) »° , 1 ,S exp ( - S ^ 1 J ( ! , ^О,  (13)

S (|)    V ° I J

+f-ln| n + V f2 +n2|

n_n ₂ (!)A ¹

n_n 1 (!) J

где

S ( l ) =

_ (X (!) + a (!) V f2 +n0(l)X ‘(!) -ПоС!)^ ‘(I) )2 +

+ ( y ( ! ) + a ( ! ) V f ² +n 2 ( ! ) y '( ! ) +n o ( ! ) x '( I ) ) ²,

S 7! ) _ 2 [ 1 + a ²( ! ) +     a ^{( ! ) f 2} _/2 x

L (f2 +n2(!))

x ( x ( ! ) x '( ! ) + Y ( ! ) Y '( ! ) ) ] .

Подставив в (13) выражение для якобиана (5), получим дифференциальное уравнение для функции а ^{( ! ):}

На основе формул (3), (18) был проведен расчет эйконала для фокусировки в отрезок при следующих параметрах: d = 60Д R = 50^, f = 50^, длина волны Z = 1 мкм. Полученная функция эйконала в декартовых координатах, взятая по модулю X, приведена на рис. 1. На рис. 2 представлена расчетная функция линейной плотности энергии вдоль отрезка фокусировки. Для сравнения на рис. 2 пунктирной линией показана линейная плотность, формируемая для случая параксиального приближения.

da (!) _    1    [XI (!) № x d!    V f2 +n2(!) L °। Iо ч 2n

x exp

' Ss>'

° I

V I J

-n o ( ! ) ( a ²( ! ) + 1 ) K ( ! )

3. Фокусировка в отрезок и дугу окружности

Рассмотрим фокусировку в отрезок

x ( ! ) = ^!- d -,0, f J , !e [о, d ]

Рис. 1. Функция эйконала для фокусировки в отрезок в случае равномерного освещающего пучка

с постоянной линейной плотностью. Апертуру будем считать круглой с радиусом R а интенсивность падающего пучка - постоянной, 1 ₀ ( u ) _ 1 ₀. Для отрезка (15) криволинейные координаты (2) имеют вид:

и = !- d + a ( ! ) V f ² +n ²,

v = n.

В этом случае пределы интегрирования по п определяются из биквадратного уравнения, полученного подстановкой (15) в (9):

n ⁴ ( a ²( ! ) + 1 ) 2 +n ² ( 2 ( a ²( ! ) + 1 ) x

x ( X ² ( ! ) + a ² ( ! ) f ² - R ² ) - 4 a ²( ! ) X ² ( ! ) ) +      (17)

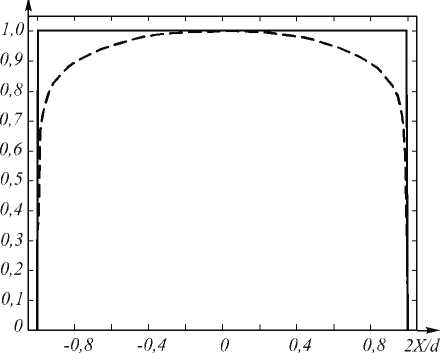
Рис. 2. Нормированная линейная плотность вдоль отрезка фокусировки в случае круглой апертуры фокусатора

+ ( X ²( ! ) + a ²( ! ) f ² - R ² ) ²

^^^^^^s

- 4 a ²( ! ) X ²( ! ) f ² = 0.

В параксиальном приближении функция a(ξ) определяется из уравнения dad)=nR2i2dr (5 d +^f.i. (19)

d 5 f V               ²        ' )

Уравнение (19) получено подстановкой первого уравнения из (16) в закон сохранения светового потока в параксиальной форме

ξ              u (ξ) R ² - u ′ ²

J Id 5' = J J 1 0 du'dv '                      (20)

0            - R      2 2

- R - u

Рис. 2 показывает, что непараксиальный эйконал обеспечивает формирование постоянной линейной плотности. При использовании параксиальной функции a ( ξ ) (19) линейная плотность спадает к концам отрезка.

Линейная плотность также рассчитывалась в рамках скалярной теории дифракции. Расчет производился по формуле

I norm -

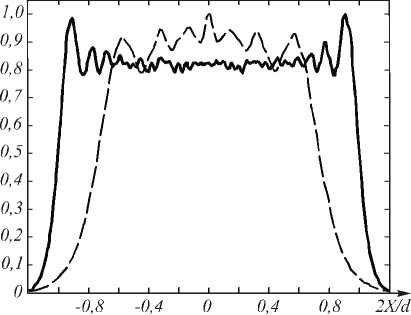
Рис. 3. Нормированная линейная плотность вдоль отрезка фокусировки в случае круглой апертуры

ε/2

I ( x ) = J E ( x , У , f )d У,

-ε/2

где ε >> ∆ , ∆ = λ f / R – дифракционная ширина отрезка фокусировки, а функция интенсивности E ( x , y , f ) рассчитывалась с использованием непараксиального интеграла Кирхгофа:

E ( x , y , f ) =

= ^{- ik}    I ₀ exp ( ik ψ ( u ) )

2 π

D

exp ( ikL ) f d u LL

где k = 2 ^π , L = ( x - u )² + ( y - v )² + f ² . λ

На рис. 3 сплошной линией представлен результат расчета линейной плотности (21), (22) в приближении Кирхгофа для непараксиального эйконала. Пунктирной линией изображена линейная плотность при параксиальном эйконале.

Сравнение результатов, полученных непараксиальной и параксиальной функций эйконала, показывает, что и в приближении Кирхгофа непараксиальный эйконал также обеспечивает значительно более равномерную линейную плотность вдоль отрезка фокусировки.

Рассмотрим случай фокусировки в отрезок (15) гауссовского пучка (11). Дифференциальное уравнение (14) в этом случае принимает вид:

da(ξ) =      1      × dξ      f2+η20(ξ)

×

σ I π S ′′ ( ξ ) exp d 2

Sv

σ

V ¹ 7

где S ( ξ ) = ( X ( ξ ) + a ( ξ ) f ² +η ²₀( ξ ) ) ² +η ²₀( ξ ).

Расчетная функция эйконала в декартовых координатах, по модулю λ, представлена на рис. 4. Расчет проводился при следующих параметрах: d = 60λ, R = 50λ, f = 50λ, σ I = 20λ, λ = 1 мкм.

Рис. 4. Функция эйконала для фокусировки в отрезок в случае гауссовского освещающего пучка

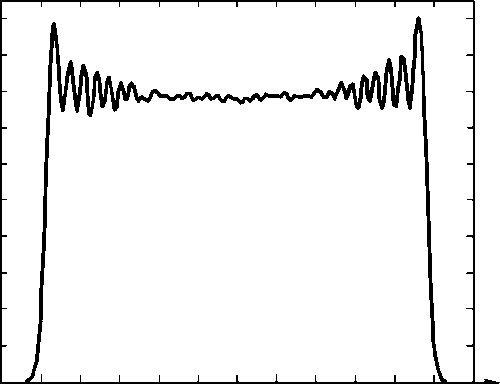
На рис. 5 представлен результат расчета линейной плотности I ( x ) вдоль отрезка в приближении Кирхгофа для случая гауссовского пучка.

Линейная плотность является достаточно равномерной. Небольшой провал в середине отрезка объясняется приближенным вычислением интеграла (6) методом Лапласа.

Также был произведен расчет эйконала из условия фокусировки в дугу окружности

X ( 5 ) = R 1 sin if 5- d 2 I / R 1 I ,

VV A 5e [0, d ]     (24)

Y ( 5 ) = R 1 cos if 5- d I / R 1 I - R 1 ,

ϕπ где R =    – радиус дуги, φ – угловой размер дуги.

1 180

Расчет проводился для равномерного пучка с круг-

лой апертурой. В этом случае для расчета а ( £ ) использовалось общее уравнение (10).

1,0 0,9

0,8 0,7

0,6 0,5 0,4

0,3 0,2 0,1

О

-0,8    -0,4     0     0,4     0,8 2X/d

Рис. 5. Нормированная линейная плотность вдоль отрезка фокусировки для случая гауссовского освещающего пучка

На рис. 6 приведено расчетное распределение эйконала при следующих параметрах: λ = 1 мкм, d = 40λ, R = 50λ, f = 50λ, φ = 120º.

Рис. 6. Функция эйконала для фокусировки в дугу в случае равномерного освещающего пучка

На рис. 7 представлен результат расчета интенсивности в плоскости фокусировки в приближении Кирхгофа для эйконала, рассчитанного из условия фокусировки в дугу окружности при равномерном освещающем пучке. Рис. 7 показывает высокое ка- чество фокусировки в дугу окружности.

Рис. 7. Распределение интенсивности в плоскости фокусировки в приближении Кирхгофа от фокусатора в дугу окружности

4. Расчет преломляющих элементов

Предложенный метод расчета эйконала может быть применен для расчета преломляющих оптических элементов. Пусть распределение эйконала ^ ( u ) в плоскости z = 0 рассчитано из условия фокусировки в заданную область. Оптический элемент будем считать расположенным непосредственно перед плоскостью z = 0. Нижнюю поверхность оптического элемента со стороны падения пучка будем считать плоской (рис. 8). Тогда, пренебрегая изменением освещенности входного пучка при прохождении через оптический элемент, сведем задачу расчета оптического элемента к расчету верхней преломляющей поверхности элемента из условия формирования заданного эйконала ^ ( u ) в плоскости z = 0.

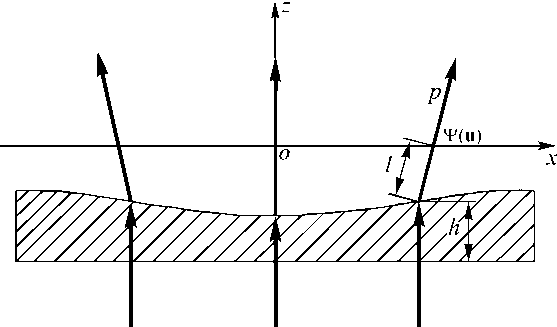
Рис. 8. Геометрия преломляющего оптического элемента для фокусировки пучка с плоским волновым фронтом

Эйконал v(u) определяет направления распро- странения лучей в виде

Р(u) = I Vv(u) J1 -(Vv(u))2

где Vy ( u ) =

( N( u ) э _¥ ( u ) )

d u     Э v

Запишем уравнение верхней преломляющей поверхности в виде

S ( u ) = r ( u ) - 1 ( u ) Р ( u ) ,

где S ( u ) = ( x ( u ) , y ( u ) , z ( u ) ) - вектор поверхности в координатах u = ( u , v ) , r = ( u , v ,0 ) - радиус вектор точки в плоскости z = 0, p ( u ) = ( p_x ( u ) , p y ( u ) , p_z ( u ) ) - вектор направления луча, определяемый по формуле (25), l ( u ) - расстояние от точки плоскости z = 0 до преломляющей поверхности по направлению p ( u ) . Функция l ( u ) в (26) определяется из уравнения

у(u) = l(u) + nh(u), (27) где n - коэффициент преломления материала оптического элемента, h (u) - толщина оптического элемента. Уравнение (27) определяет равенство при z = 0 оптических длин лучей, прошедших через эле- мент, заданному эйконалу ^(u). Толщина оптического элемента может быть записана через функцию l (u) в виде

h (u) = -Pz (u) l (u)- z0 ,

где z ₀ – координата нижней границы оптического элемента. Из (27), (28) получим функцию l ( u ) в виде

^{l ( u} ) =

^ ( u ) + nz 0 ^{1 -} nP z ( u )

Таким образом, преломляющая поверхность для формирования заданного эйконала ^ ( u ) имеет вид (26), (29). Отметим, что эйконал ^ ( u ) в плоскости z = 0 определен с точн остью до константы. Эта константа должна выбираться из условия, чтобы в ерхняя преломляющая поверхность в точке с наибольшей толщиной касалась плоскости z = 0. В этом случае предположение о том , что освещенность входного пучка при прохождении через оптический элемент слабо меняется, имеет наименьшую ошибку. На рис. 8 элемент расположен несколько ниже плоскости z = 0 только из соображений наглядности при выводе формул преломляющей поверхности.

На рис. 9, 10 представлены преломляющие поверхности, восстановленные по эйконалам, рассчитанным из усл овия фокусировки в отрезок и дугу окружности, соответственно. В случае фокусировки в отрезок расчет эйконала производился при следующих параметрах: d = 10мм, R = 25мм, f = 50мм.

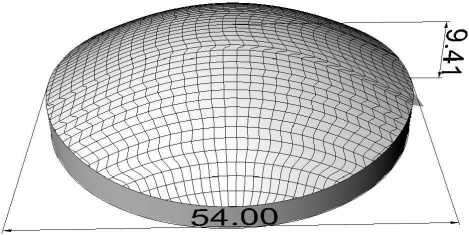
Рис. 9. Преломляющий элемент для формирования распределения освещенности в виде отрезка

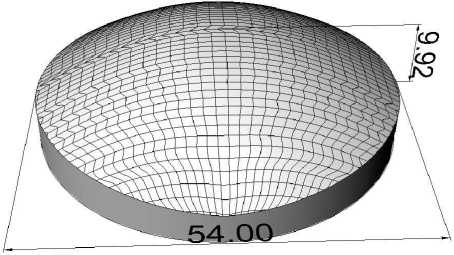
Рис. 10. Преломляющий элемент для формирования распределения освещенности в виде дуги окружности

При фокусировке в дугу окружности расчет производился при параметрах: d = 10мм, R = 25мм, f = 50мм, φ = 100º.

Работа рассчитанных оптических элементов была промоделирована средствами специализированной программы по светотехнике TracePro [11]. На рис. 11, 12 представлены распределения освещенности, полученные в результате моделирования работы полученных элементов в пакете TracePro.

Total - Illuminance Map for Incident Flux exit plane Surface 0 Global Coordinates

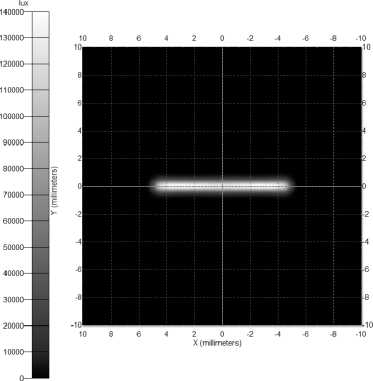
Illuminance Min:1.7702e-014 lux, Max:1.3962e+005 lux, Ave:2277.7 lux, RMS: 14502, Total Flux:0.91109 Im 10000 Incident Rays

Рис. 11. Результаты моделирования работы преломляющего элемента для формирования распределения освещенности в виде отрезка в TracePro

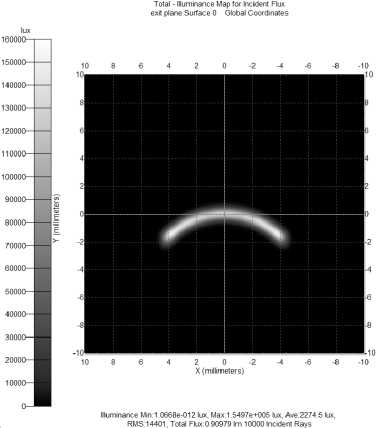
Рис. 12. Результаты моделирования работы преломляющего элемента для формирования распределения освещенности в виде дуги окружности в TracePro

Рис. 11, 12 показывают высокое качество фокусировки в отрезок и дугу окружности соответственно.

Заключение

Расчет функции эйконала из условия фокусировки в произвольную кривую в непараксиальном случае сведен к решению обыкновенного дифференциального уравнения первого порядка, разрешенного относи- тельно производной. Проведен расчет эйконалов из условия фокусировки в отрезок и дугу окружности для случаев равномерного и гауссовского освещающих пучков. Показано, что непараксиальный эйконал обеспечивает значительно более равномерную линейную плотность вдоль отрезка по сравнению с параксиальным решением. Функции эйконала могут быть использованы для расчета преломляющих оптических элементов, предназначенных для фокусировки в кривые. Приведенные примеры расчета оптических элементов для фокусировки в отрезок и дугу окружности показывают высокую работоспособность такого подхода.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), гранта Президента РФ поддержки ведущих научных школ (НШ-3086.2008.9) и грантов РФФИ № 07-07-91580-АСП_а, 08-07-99005-р_офи, 09-07-92421-KE и Фонда содействия отечественной науке.