Геостатистический анализ микроструктуры горных пород с использованием метода разложения по сферическим гармоникам

Разработка, нефтяных и газовых месторождений опирается на. геологическое моделирование, базирующееся в свою очередв на. петрофизических фильтрационно-емкостных свойствах коллекторов [1]. В настоящее время для нахождения петрофизических свойств активно используется метод рентгеновской микротомографии, позволяющий строить трехмерные модели горных пород с большим разрешением. Обычно используемое в петрофизических исследованиях разрешение 1-8 мк/1 воксель.

Из-за. сравнительной новизны этого метода, и отсутствия научно обоснованных методов обработки такого рода данных большой объем информации, содержащийся в микротомограммах, недостаточно изучен и нуждается в систематизации. Так как микротомограммы горных пород, по сути, представляют собой случайные трехмерные объекты, для анализа, и систематизации информации на. масштабах 1 мк и выше предлагается применить геостатистические методы. Однако в связи с тем, что традиционная геостатистика была в значительной степени связана с макромасштабами, работа с информацией на микроуровне требует либо существенной модификации классических подходов, либо создания новых методов, более адекватных реальным микротомограммам.

Настоящая работа, посвящена, геостатистическому анализу свойств микроструктуры горных пород, которые могут служить коллекторами жидких и газообразных углеводородов. Анализируются закономерности поведения полей вариограмм для оценки: а.) корреляционных длин микроструктуры; б) анизотропии пород на. различных масштабах.

2.    Данные

В качестве объекта, исследования выступают микромодели горных пород, полученные при помощи рентгеновской микротомографии. Изначально результаты рентгеновского сканирования — это набор двумерных полутоновых изображений, характеризующих распределение коэффициента, поглощения рентгеновского излучения в исследуемом образце (яркость каждого элемента, полутонового изображения соответствует значению коэффициента.

поглощения в пределах этого элемента). Необходимый препроцессинг данных состоит из двух шагов, которые схематически изображены на рис. 1:

• 1)    бинаризация с заданным по измеренной пористости пороговым значением (пора заполнена воздухом, и его коэффициент поглощения много менвше коэффициента поглощения породы);

• 2)    «сборка» трехмерной модели из набора изображений.

  

  Рис. 1. Схема получения модели данных

  
  
3.    Поле вариограммы

Модели представляет собой трехмерную сетку, в каждой ячейке которой находится либо пора (черный вокселв), либо порода (белый вокселв). В итоге микроструктура образца описывается индикаторной функцией

1 (x,y,z) = |

1, если в ячейке с координатами {x,y,z } находится нора 0, если в ячейке {x,y,z } находится порода.

Геостатистика базируется на статистической интерпретации данных. Предполагается, что данные измерений и (х^ ) являются реализациями случайной функции V(х^ ), которая описывается некоторой функцией распределения. Для описания пространственной корреляции таких данных чаще всего исполвзуется вариограмма. Это статистический момент второго порядка, характеризующий вариацию разницы значений функции, т.е. математическое ожидание квадрата разности значений функции в точках, разделенных определенным вектором (так называемым лэгом) [2]:

₇(^Х) = |я (|V(Х + h) -V(Х)|) VX.                           (2)

В одномерном случае вариограммы выглядит следующим образом (рис. 2) и описывается такими параметрами, как:

• •    порог — значение, к которому асимптотически приближается модели вариограммы;

• •    радиус корреляции (корреляционная длина) — расстояние, при котором модель вариограммы выходит на пороговое значение. Радиус корреляции важен для нас тем, что характеризует размер неоднородностей;

• •    эффект самородков — величина, к которой стремятся значения вариограммы для лэгов вблизи нуля (непосредственно в нулевой точке вариограмма равна нулю).

4.    Разложение по мультиполям (сферическим гармоникам)

В нашем случае в качестве случайной функции выступает индикаторная функция I(x,y,z ), определенная в (1). Соответственно вариограмма для нашей модели представляет собой трехмерное поле /(h) (где h = (h_x, h_y, h_z ) — лэг), которое мы будем анализировать путем разложения по сферическим гармоникам.

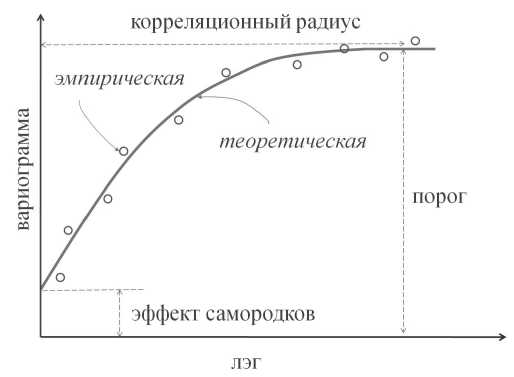
Рис. 2. Вариограмма и ее параметры

Разложение по мультиполям (по сферическим гармоникам) часто используется для изучения электрических и магнитных полей, полей механических напряжений, космического излучения, рельефа, других полей, заданных в виде карты на сферической поверхности. Для описания поля в трехмерном пространстве коэффициенты мультипольного разложения могут быть записаны как функции от расстояния [3].

Мультипольное разложение выражается как сумма термов (гармоник) с последовательно усиливающейся зависимостью от угла: нулевая гармоника (монопольный момент) не зависит от угла, меняется в зависимости от углов, высшие гармоники (квадрупольный, октупольный моменты) меняются в зависимости от угла быстрее, чем первая гармоника (дипольный момент).

Чаще всего мультипольное разложение записывается как сумма сферических гармоник [4]. Сферические гармоники представляют собой собственные функции оператора Лапласа на единичной сфере и имеют вид [5]:

^т (1 - Л\^{)! т)!} ртр^ AV^W Y_t -^21 + 1)_(г + т/1 ^{(cos 9)е}

где F™ (cos 9) — присоединённые многочлены Лежандра, P_t^т — (—1)^m (/-Д)! ^?” • Сферические гармоники ортонормальны:

7Т    2 л

/./

0 =0 ( =0

*               _

У ^т У т dQ — di и 5_т ,

^        ^                          Lt     IILit L 7

где 5 — символ Кронекера, a dQ — sin 9dyd9.

Соответственно, если / (9, у) — известная интегрируемая в квадрате на единичной сфере функция, аппроксимация этой функции задается в виде [4-5]:

го I

/ (9, у) — ТТ ^ К^т (9, у).                      (4)

I =0 т =- 1

Коэффициенты разложения выражаются следующим образом:

2 л

7Т

-] ч

d9 sin 9 •/ (9, у) •У™ (9/ у).

Разложение по сферическим гармоникам связано с симметрией физических полей относительно группы вращения. Известно, что существует взаимно однозначное соответствие между сферическими функциями порядка I и линейным представлением группы вращения порядка I [6-7] и, соответственно, между сферическими функциями порядка I и анизотропией порядка I [8].

5.    Разложение поля вариограммы по сферическим гармоникам

Итак, для анализа поля вариограммы мы перейдем от декартовых координат ж, у, г к сферическим координатам T,9,p и для каждого фиксированного т разложим поле по сферическим гармоникам.

Как нетрудно видеть из (2), поле вариограммы симметрично относительно начала ко-

—

—

ординат: /(^) = /(—^), откуда получим для сферических координат (для каждого фиксированного т):

^/(^p)^^{(л — 9,}p ^{+ л)}.                              (6)

В силу этого сумма коэффициентов с I = 1 будет равна нулю. Покажем это ниже.

Из (5) получим явное выражения для коэффициента с I = 1; m = — 1 и преобразуем его:

27Г        7Т

27Г        7Т

/- 1

= j dp j d9 sin 9 •/(9,p) • Kf¹* (9, p) = - ^ dp j d9 sin 9 •/(9,p) • У 1 ¹ (9,p).

Подставив явное выражение У1 ¹ = 2-^21 sin 9е ^г1р в [5], получим

/-1

______ 2тт        7T

= 2\1Ь 1 dp j d9 sin² 9 • e^w • / (9,p).

Аналогично,

/ 11 =

_  2тт        7T

— 2у2л / dp / d9 sin² 9 • е-^г^ •/(9,p).

Тогда

2-k

^⁺я=2 VI / 0

7Т dp J d9 sin2 9•/(9,p)^ (ег1р

_______ 2тт        7Т

— е - ^г^) = г^ IL J dp J d9 sin² 9 •sinp• /(9,p).

Разбив интеграл на две части, запишем

/- 1 + / 11 = i

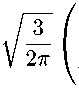
2^      7T                                   \ d9 sin2 9 • sinp •/(9,p) + j* dp j* d9 sin2 9 • sinp •/(9, p) I ,

откуда заменой пределов интегрирования получим

_____ 7Т         7Т

/-¹ + / 1 ¹ = i 2Л j dp j d9 sin² 9 • sinp • (/(л — 9,p) — /(л — 9, p + л)). 00

Так как sin²(л — 9) = sin² 9, а интеграл от 0 до л равен интегралу от л до 0.

_____ 7T         7T

/Г¹ + / 1 ¹ = i \j 23л J dp Jd9 sin² 9 • sinp • (/(л — 9,p) — /(л — 9,p + л)). 00

Сложив выражения (7) и (8) и разделив результат на два, получим, что

___ 77

Л”¹+Л¹ = |у2Г У ^dP j ^d6 sin^{2 6} •sin p • ^{(/ ( 6,} p') - $ ^{( 6,} p ⁺ г ⁾⁺ $ ⁽r ^{- 6,}p) - $ ⁽r ^{- 6,}p ⁺ г )) = °^-

Аналогичным образом получим сначала, что

$0 = 2j dp jdO sin 6 •/ (6,p) a (6,p) = - 4 УГ 2j dp jd9 sin26 •/ (6,p), 0000

а затем

___ 2-777

Л⁰ = 8 У | У dtp I d6 sin 26 • (/(7Г - 6,p + г ) - /(6, p)) = °.

Таким образом, /—¹ + / q + /¹ = °. Поэтому в следующем разделе мы будем рассматривать только гармоники с I = ° и I = 2.

6.    Результаты

Для иллюстрации метода будем использовать четыре образца.

Рис. 3. Первый образец, искусственный слоистый образец. Белые участки обозначают породу, серые — поры

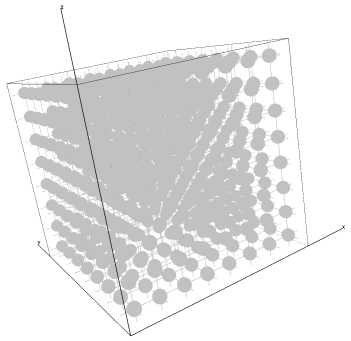
Рис. 4. Второй образец, искусственный образец со сферическими порами. Белые участки обозначают породу, серые — поры

Рис. 5. Третий образец, песчаник. Белые участки обозначают породу, серые — поры

Рис. 6. Четвертый образец, естественный образец с выраженной анизотропией. Белые участки обозначают породу, серые — поры

• •    Искусственный слоистый образец, размер 1024 х 1024 х 1024 вокселей, пористость 22.69% (рис. 3).

• •    Искусственный образец со сферическими порами, размер 1024 х 1024 х 1024 вокселей, пористость 6.62% (рис. 4).

• •    Песчаник, размер образца 1024 х 1024 х 1024 вокселей, разрешение сканирования 2.5 мк/воксель, пористость 22.02% (рис. 5).

• •    Естественный образец с выраженной анизотропией, размер образца 1024 х 1024 х 1024 вокселей, разрешение сканирования 2.32 мк/воксель, пористость 9.89% (рис. 6).

Рассмотрим сначала графики нулевой гармоники /0° (рис. 7, рис. 8, рис. 9 и рис. 10 для образцов с первого по четвертый соответственно).

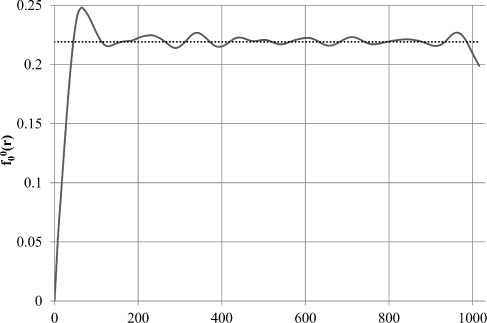
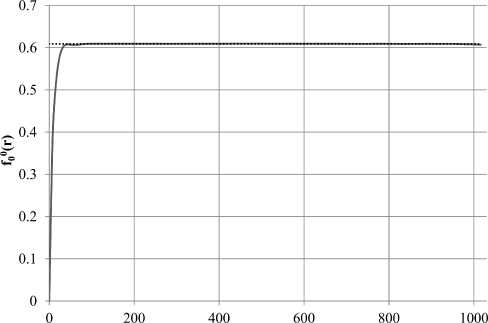
Как уже было отмечено, выход вариограммы на асимптотику характеризует размер неоднородности. На рис. 7 мы видим, что график нулевой гармоники для слоистого образца сначала поднимается к некоторому пороговому значению выше асимптотики, затем спускается ниже асимптотики, а между ними можно видеть несколько небольших псевдопорогов — это говорит нам о многомасштабности. В утрированном виде можно наблюдать это на графике для искусственного образца со сферическими порами (рис. 8): здесь псевдопороги появляются на расстояниях, кратных периоду структуры образца. В дальнейшем предполагается получать спектр корреляционных длин при помощи разложения по экспонентам. Для песчаника (рис. 9) виден только один существенный порог, и он согласуется с теоретической асимптотикой. Для анизотропного естественного образца (рис. 10) мы видим, что график нулевой гармоники ведет себя таким же образом, как и для слоистого искусственного образца, но более плавно: сначала подъем к одному пороговому значению, затем спуск к другому порогу. То есть для этого образца можно предположить две основных корреляционных длины и, соответственно, два характерных размера неоднородности, и это согласуется с тем, что мы можем наблюдать визуально на рис. 6: в образце участки более-менее равномерного распределения пор перемежаются с участками сплошной породы.

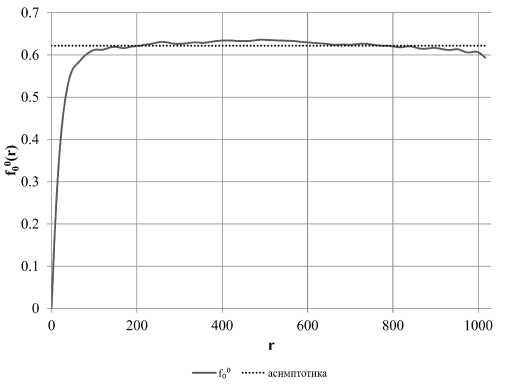
Рис. 7. Сплошная линия — график /0 для слоистого образца, точечная линия — теоретическая асимптотика

На рис. 11, рис 12, рис. 13 и рис. 14 изображены коэффициенты разложения по сферическим гармоникам с I = 2 на фоне /(0. Для заведомо анизотропного искусственного слоистого образца (рис. 11) коэффициенты с I = 2 на некоторых г сравнимы по величине с нулевой гармоникой, т.е. можно говорить о наличии анизотропии на определенных масштабах. Для изотропного искусственного образца со сферическими порами (рис. 12) коэффициенты с I = 2 пренебрежимо малы. Для песчаника (рис. 13) высшие гармоники также сравнительно малы. Для анизотропного естественного образца мы, как и ожидалось, видим, что при г, сравнимых с размером образца, вторая гармоника существенна.

----f0° .......асимптотика

Рис. 8. Сплошная линия — график /0° для искусственного образца со сферическими порами, точечная линия — теоретическая асимптотика

г

То° .......асимптотика

Рис. 9. Сплошная линия — график /0° для песчаника, точечная линия — теоретическая асимптотика

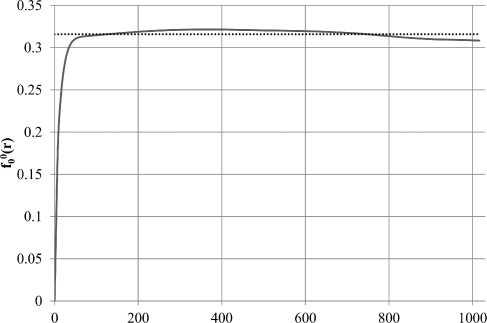
Рис. 10. Сплошная линия — график /0° для естественного образца с выраженной анизотропией, точечная линия — теоретическая асимптотика

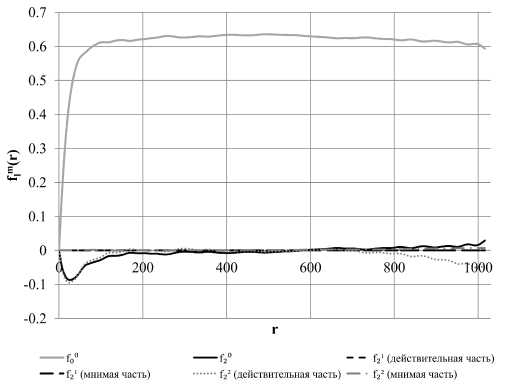
Рис. 11. Графики гармоник для слоистого искусственного образца

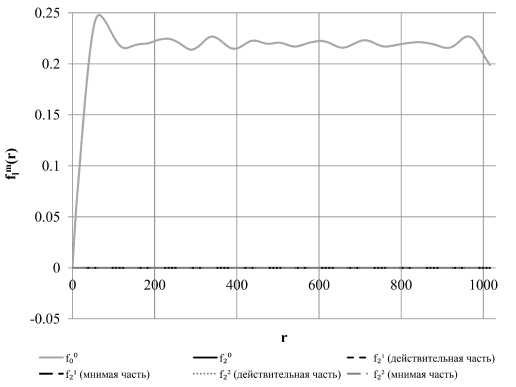
Рис. 12. Графики гармоник для искусственного образца со сферическими порами

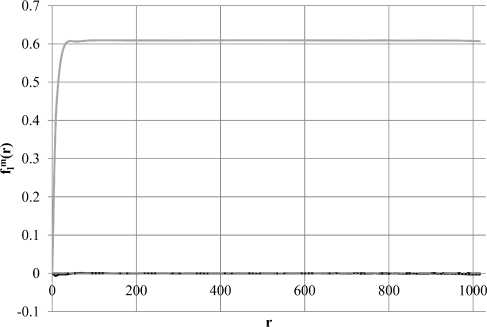
f0°                             f2°                       - - f2* (действительная часть)

ТТ (мнимая часть)        .......f22 (действительная часть) — • f22 (мнимая часть)

Рис. 13. Графики гармоник для песчаника

Хотя здесь мы говорим только качественно о наличии анизотропии на определенных масштабах, информации о высших гармониках достаточно и для определения направлений анизотропии, это является объектом нашего дальнейшего исследования.

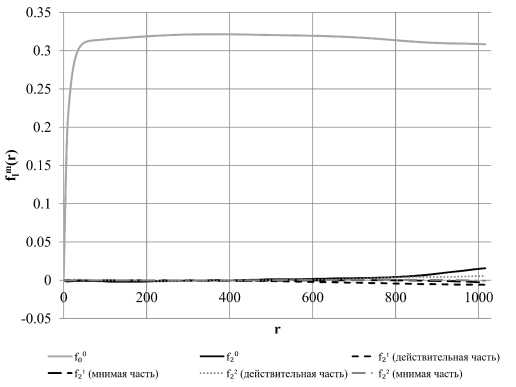
Рис. 14. Графики гармоник для естественного образца с выраженной анизотропией

7.    Заключение

В ходе работы была исследована возможность применения вариограммного анализа для оценки степени изотропности микроструктуры горных пород. Были выявлены многомас-штабность микроструктуры породы и анизотропия на определенных интервалах масштабов.

В дальнейшем на основе текущих результатов планируется получить:

• •    спектр корреляционных длин при помощи разложения по экспонентам нулевой гармоники;

• •    информацию о направлениях анизотропии из высших гармоник.

Таким образом, геостатистический анализ может быть перспективным методом для классификации и систематизации микроструктур литофаций коллекторов.