Гибридный алгоритм распознавания образов и его свойства

При решении задач распознавания образов различают два типа исходной информации: априорные сведения о виде уравнения разделяющей поверхности и обучающая выборка, составленная из значений признаков классифицируемых объектов и соответствующих им «указаний учителя». Известные подходы к синтезу решающего правила классификации ориентированы в основном на определенный тип исходных данных, что при условиях, отличающихся от априорных предположений, приводит к снижению их эффективности. Так, в параметрических алгоритмах за основу принимаются сведения о виде уравнения разделяющей поверхности (ее аналитический вид), то для непараметрических процедур достаточно знание лишь ее качественных характеристик и информации обучающей выборки.

Для решения проблемы эффективного использования априорной информации предлагаются гибридные системы распознавания образов, которые обеспечивают сочетание в обобщенном решающем правиле классифи-

из условия минимума эмпирической ошибки распознавания образов

n

Р^(а) = n ⁴ S1 ( ° x), ° x ) ) , j =1

где индикаторная функция

А , jx", jA ¹ если °⁽ x ) * °⁽ x X 1 ( о( x¹ ), а( x¹ ) ) = (                . _ .

[ 0, если °( x¹ ) = °( x¹ );

°( x¹ ) - «решение» правила (1) о принадлежности ситуации x к тому или иному классу.

По результатам вычислительного эксперимента сформируем выборку расхождений V = ( x i , q ( x i ), i =1 , n ) между «решениями» °( x i ) правила (1) и «указаниями учителя» °( x i ) из обучающей выборки V . При этом значения функции расхождений

кации преимуществ параметрических и локальных методов аппроксимаций, основанных на оценках плотности вероятности типа Розенблатта-Парзена [1].

Синтез гибридного алгоритма распознавания образов. Пусть исходную информацию при решении двухальтернативной задачи распознавания образов составляют обучающая выборка V = ( x i , о( x i ), i = 1, n ) и априорные сведения F 2 ( x , а) о виде уравнения разделяющей поверхности f₁₂ ( x ) между классами Q 1 , Q 2 в пространстве _{x e} R^k . Знание F ₂ ( x , а) предполагает наличие решающего правила классификации

' 0 V о( x i ) = °( x i ),

q ( x i ) = < ( F₁₂( x i , а) + a ) V °( x i ) =- 1 и °( x i ) = 1,

- (F₁₂( x i ,а) + A ) V °( x i ) = 1 и °( x i ) = - 1.

_F ' x еЦ , если F_n( x , а) <  0, m_n : )                                         (1)

[ x e Q ₂, если F₁₂ ( x , а) >  0,

по тем или иным причинам не удовлетворяющего исследователя. Информация обучающей выборки V формируется на основании данных о значениях признаков x классифицируемых объектов и соответствующих им «указаний учителя»

°(x ) =

- 1, если x eQ , 1, если x e Q ₂ .

Для использования в полном объеме априорной информации ( F ₂( x , а), V ) воспользуемся принципами гибридного моделирования, которые обеспечивают сочетание в обобщенном решающем правиле классификации преимущества параметрических и локальных методов аппроксимации.

Для этого определим параметры а уравнения разделяющей поверхности F ₂( x , а) решающего правила (1)

При наличии ошибки, функция расхождения принимает значение обратное по знаку уравнения разделяющей поверхности F ₂ ( x , а) и превышает его на величину A . Например, если ситуация x i принадлежит второму классу (°( x i ) = 1), а в соответствии с решающим правилом (1) классифицируемый объект с признаками x i e Q 1 , т. е. F ₂( x i , а) <  0, то значение функции расхождения в ситуации x соответствует q ( x i ) = F ₂ ( x i , а) + A .

Восстановление функции q ( x ) по выборке V осуществляется на основе непараметрической регрессии [2]:

n

_   S q ⁽ x W ^x )

q ^{( x} ) = , S P i ( x ) i =1

т — г ( X — X i ^

P i ( x ) = П ф|-1_^ I,            (4)

v =1     \ c V /

где Ф ( - ) - ядерная функция, удовлетворяющая условиям положительности, симметричности и нормированности [1].

Тогда гибридный алгоритм классификации запишется в виде

m 12 ( x ): <

x e Q1,

x e Q2,

если f 12 < x ) <  0, если f ₁₂( x ) >  0,

где

f 12 ⁽ x ) = F 2 ⁽ x ,^а) + q ⁽ x )-

Оптимизация алгоритма (5) по параметрам размытости c _v, v = 1, к ядерных функций Ф ( - ) и А осуществляется из условия минимума статистической оценки ошибки распознавания образов типа (3).

Меняя вид функции q ( x ) , обеспечивающей коррекцию F 12 ( x , а), можно получить семейство гибридных решающих правил [3].

Асимптотические свойства гибридных решающих функций. Рассмотрим асимптотические свойства гибридных уравнений разделяющих поверхностей / 1 ₂ ( x ) V x е R¹ при известной совместной плотности вероятности p ( x ) распределения x в классах Q 1 , Q ₂.

Предположим, что f12(x), F(x,а),p(x) ограничены и непрерывны со всем своими производными до второго порядка включительно. Эти условия, налагаемые на f12 (x), F(x, а), p(x), обозначим через G2.

Теорема. Пусть: 1) уравнение разделяющей поверхности f12 (x), ее аппроксимация F(x, а) и совместная плотность вероятности p(x) распределения x в классах удовлетворяют условиям G2; 2) ядерные функции Ф (u) > 0 в непараметрической статистике (4) являются симметричными и нормированными, причем значение JumФ(u) du при m > 2 ограниченно и равно 1 при m = 2; 3) последовательности c = c(n) ^ 0, А = А(n) ^ 0 при n ^ да , а nc ^ да.

Тогда гибридная модель f12 (x) (6) обладает свойства- ми асимптотической несмещенности

( q ( x ) p ( x ) ) ⁽²⁾ ₂

M ( f 2^{( x} ) ^- У 7( ^x ) ) ~              c ^{+ A}

² p ( x )

и сходимости в среднеквадратическом

M ⁽ f 2 ^{( x} ) - Л( ^{x )) 2} ~ ( ncp ^{( x} ) )^{- 1} q ^{2( x} ) ||^Ф ( ^u )| |^{2 +}

+ с ⁴ ( ( q ^{( x} ) p ^{( x} ) ) ⁽²⁾ ) ( ⁴ p ^{2 (} u ) ) 1 +

₊ ( q ( x ) p ( x )r c , A ₊ A, p ^{( x} )

Здесь ( q ( x ) p ( x ) ) ⁽²⁾ - вторая производная по x произведения функций в скобках; M - знак математического ожидания; ||ф( и )|| = J Ф ² ( u ) du •

Справедливость приведенных утверждений определяет состоятельность статистики f 1 ₂( x ).

Доказательство основано на методике, предложенной в работе [4] при исследовании гибридных моделей стохастических зависимостей.

Анализ результатов вычислительных экспериментов. Исследовалась двуальтернативная задача распознавания образов к -мерном пространстве признаков ( к = 2,10). Законы распределения признаков в области первого класса формировались в соответствии с датчиком случайных чисел

I i Л I 6       — x = m + о ^е -0,5p .— , v = 1, к,

IJ V3 p при p = 12; m = 3; s е[0;1] - случайная величина с равномерным законом распределения; о = 1.

Значения признаков второго класса генерировались с использованием датчиков случайных чисел xv = a + s (b - a), xv+1 =(xv)2 -6xv +10 + 0 |Ssi -0,5p I-1= где v е Iн - множество нечетных чисел меньших к , a = 1,5, b = 4,5.

Исходные сведения о виде решающей функции представлялись полиномом

F ( x , a ) = S Г ^xv +1 ^- ( ( ^xv ) ^{2 - 6 x}v ^{+ 10,8} ) 1.

V е 1 н

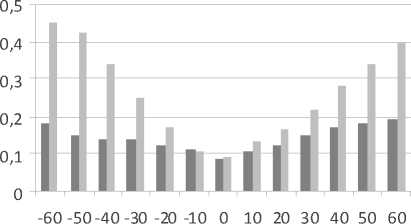
Результаты вычислительных экспериментов представлены на рисунке. По горизонтальной оси отложено относительные (%) отклонения параметров решающей функции F ( x , а ) от оптимальных, по вертикальной оси -оценки вероятностей ошибок распознавания образов.

0,5

0,4

0,3

0,2

0,1

гггггптгггг

-60 -50 -40 -30 -20 -10 0 102030405060

б

Зависимость оценок вероятностей ошибок распознавания образов гибридного (столбец 1) и параметрического (столбец 2) алгоритмов отклонений параметров исходной решающей функции от оптимальных. Размерность пространства признаков: к = 2 ( а ); к = 4 ( б )

Из анализа данных на рисунке следует, что гибридный классификатор обладает значительной устойчивостью к отклонениям параметров исходной решающей функции от оптимальных. Например, для к = 2 при отклонении параметров решающей функции от оптимальных на ± 60% оценка вероятности ошибки распознавания образов параметрического алгоритма больше гибридного на 63 %.

Таким образом, гибридные алгоритмы распознавания образов позволяют использовать информацию обучающих выборок и частичные априорные сведения о виде решающих функций на основе сочетания преимуществ параметрических и локальных аппроксимаций, основанных на ядерных оценках плотности вероятности типа Розенблатта–Парзена. Структура гибридных уравнений разделяющих поверхностей между классами в подобных системах формируется на основе параметрической ее аппроксимации, восстанавливаемой с учетом априорных сведений, и корректирующей ее функции непараметрического типа. Вид корректирующей функции и особенности исходной информации порождают семейство изучаемого класса систем.

Гибридные решающие функции обладают свойствами асимптотической несмещенности и состоятельности, устойчивы к отклонениям параметров исходного уравнения разделяющей поверхности от оптимальных их значений.