Гибридный асимптотический метод анализа каустик оптических элементов в радиально-симметричном случае

Дифракционные оптические элементы (ДОЭ) применяются для миниатюризации и облегчения оптических систем. Кроме того, они позволяют сформировать световые пучки с такими свойствами, которые невозможно получить с помощью классических элементов рефракционной оптики [1 –5].

Классические линзы и зеркала сложно использовать в некоторых устройствах из-за большого размера. Кроме того, формирование сложных комплексных распределений лазерных полей невозможно выполнить с помощью классических рефракционных элементов. Однако эта задача очень хорошо решается с помощью средств дифракционной оптики. ДОЭ, учитывающие волновую природу света, успешно выполняют преобразование лазерного излучения в практически произвольное амплитудно-фазовое распределение [6, 7].

Основное свойство ДОЭ – использование явления дифракции для изменения направления распространения световых лучей. Дифракционные элементы разбивают световой луч на множество лучей, каждый из которых перенаправляется под разными углами. Некоторые ДОЭ могут сочетать в себе свойства как дифракционных, так и рефракционных линз. Примером могут служить так называемые гармонические дифракционные элементы [8– 10], где дифракционные и рефракционные свойства линзы зависят от приведения фазы к различным интервалам.

В данной работе выполнено исследование ДОЭ, формирующих каустические поверхности с использованием гибридного асимптотического подхода, основанного на асимптотическом представлении интеграла Кирхгофа.

S ( x , y , u , v ) = L ( x , y , u , v ) + Ф ( u , v ) ,                 (2)

L ( x , y , u , v ) = ( x - u ) 2 + ( y - v ) 2 + z² ,             (3)

x , y , z – декартовые координаты точки наблюдения, u, v – декартовые координаты в плоскости z =0, Ф ( u , v ) – эйкональная функция в плоскости z =0, U ( x , y , z ) – комплексная амплитуда в точке наблюдения, U 0 ( u , v ) – модуль комплексной амплитуды в плоскости z =0.

Приведённый интеграл можно вычислить с помощью метода стационарной фазы.

U ( x , y , z ) = ( zU ₀ ( u ₀ , v ₀ ) / L ( x , y , u ₀ , v ₀ ) ) x

exp ( ikS ( x , y , u 0 , v 0 ) )

S uu ( ^x , y , ^u 0 , ^v 0 ) ^Svv ( ^x , y , ^u 0 , ^v 0 ) ^- I S uv ( ^x , y , ' 0 , ^v 0 ) J

где u 0 , v 0 – стационарная точка, которая определяется соотношениями

d S ( x , y , u 0 , v 0 ) = 0 d S ( x , y , u ₀ , v ₀ ) = 0 d u               d v

x = u ₀ +

^Ф u ( ^u 0 , ^v 0 )

z

Q ( ^u 0 , ^v 0 )

y = ^v 0 ⁺

^Ф v ( ^u 0 , ^v 0 )

z

Q ( ^u 0 , ^v 0 )

где Q ( u , v ) = 1 -Ф Ф u ( u , v ) -Ф v ( u , v ) .               (7)

В интеграле (4) вычислим выражение:

S uu ( ^x , y , ^u 0 , ^v 0 ) S vv ( ^x , y , ^u 0 , ^v 0 ) ^- ( S uv ( ^x , y , ^u 0 , ^v 0 ) ] ² = = ( z ²/ L ⁴) J ( u 0 , v 0 ) .

Якобиан преобразования имеет вид

1. Асимптотическое представление для интеграла Кирхгофа

^J ( ^u , ^v ) = x u y v ^- x v y u .                                  ⁽⁸⁾

U ( x , y , z ) = J ( z / L ( x , y , u , v ) ) u 0 ( u , v ) x

x exp ( ikS ( x , y , u , v ) ) d u d v ,

Функции, описывающие лучевые преобразования, входящие в якобиан, имеют вид x = x0 (u, v ) = u + ф'(u,v) z,                        (9)

y = У 0 ( ^u , V ) = V + ^{( ф} v ( u , v ) / Q ( u , v ) ) z •            (10)

При наличии нескольких стационарных точек вместо (4) получим:

Используя выражение для функции S( u , v ), получаем

U ( x , У , z ) = E U 0 ⁽ u ^{0 ,} v 0 ) exP ^f ikS ( x , У , u о , ^v о ) ) • (ⁿ) ^u о , ^v о VJ ( u 0 , ^V 0 )

d ² S ( x , y , u ₀ , v ₀ ) d ² S ( x , y , u ₀ , v ₀ )

э Ц²              d V²

- ( d ² S ( x , y , u ₀ , v ₀ ) / d u d v ) =

J ² ( u , v , z )

Выражение для интенсивности будет:

U ( x , y , z ) U *( x , y , z ) =

^f d x 0 ( u , ^v ) d y 0 ( u , ^v )

_ч d u       d v

d y 0 ( u , v ) d x 0 ( u , v ) ) ²

d u      d v

=EE u1v1 u0v0

U 0 ( u 0 , ^V 0 ) ^U o ( u p ^V 1 ) V J ^{( u} 0 , ^V 0 ) л] J ⁽ u 1 , ^V 1 )

Окончательное выражение для интенсивности принимает вид

I ( ^x , y , ^z ) = E ¹ 0 ( ^u 0 , ^v 0 ) / J ( ^u 0 , ^v 0 ) •                    ⁽²⁰⁾

x exp I ik I S ( x , y , u 0 , v 0 ) - S ( x , y , u^ V 1 )

u ₀ v ₀

После усреднения осциллирующих слагаемых выражение принимает вид

I (x, y, z ) = E I0 (u 0,v 0) /J (u 0,v 0) • u0v0

Это выражение плохо тем, что по точке прихода ( x , y , z ) нужно вычислить точку выхода ( u 0 , v 0 ), что проблематично при наличии нескольких стационарных точек.

Чтобы решить эту проблему, представим выражение (13) в несколько другом виде.

Учитывая свойства дельта-функции, выражение для интенсивности принимает вид:

В результате получили выражение, которое совпадает с выражением (13), полученным с использованием метода стационарной фазы. Таким образом, подход к расчёту интенсивности, основанный на вычислении интеграла Кирхгофа с помощью метода стационарной фазы, и подход на основе вычисления интеграла (16) методом Лапласа асимптотически эквивалентны.

2. Геометрическая оптика в радиально-симметричном случае

I ( x , y , z ) =

= J 1 0 ( x , y ) 5 ( x - x 0 ( u , v ) , y - y 0 ( u , v ) ) d u d v •

2.1. Уравнения лучей и каустик в радиально-симметричном случае

Найдём теперь лучевые уравнения в случае, если эйкональная функция имеет радиально-симметричный вид

Однако использование квадратурных формул для вычисления интегралов с сингулярными функциями тоже затруднительно.

Поэтому заменим сингулярную функцию, входящую в интегральное выражение, её регулярной аппроксимацией

8 ( x , y ) = (1/2 no ²)exp ( - ( x ² + y ²)/2 o ² ) . (15)

После постановки (15) в (14) получим следующий интеграл:

I ( x , y , z ) = (1/2 ло ²) x

x J 1 ₀ ( u , v ) exp ( - S ( x , y , u , v ) / 0 ² ) d u d v ,

где

S ( x , y , u , v ) = 0,5 { ( x - x 0 ( u , v ) ) 2 + ( y - y 0 ( u , v ) ) 2 } . (17)

Вычислим интеграл (16) с помощью метода Лапласа.

Согласно методу Лапласа для вычисления двойных интегралов от быстро убывающих функций

I ( x , y , z ) =

=E u0v0

I 0 ⁽ u 0 , ^v 0 )

d ² S ( x , y , u , v ) d ² S ( x , y , u , v ) f d ² S ( x , y , u , v ) d u ² d v ² I d u d v

x 0 ( u , V ) = u +

< y 0 (u,v ) = v +

дФ и др P

A 1 1 -(|^ф) ²

\ ^{( d}P ) дФ v др ^р

1 - ^дф) ²

V ( др )

Введём в области начального распределения эйконала полярные координаты

u = р cos ф , v = р sin ф .

А также ввёдем полярные координаты в области прихода лучей

x ₀ ( u , v ) = R cos 6 , y ₀ ( u , v ) = R sin 6 .

Подставляем (22), (23) в (21) и получаем

R cos 6 = р cos ф

1 +

дФ 1 др ^р

<

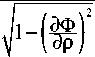
R sin 6 = р sin ф

1 +

дФ 1 др р

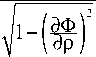
Решения полученной системы имеют вид:

дФ 1

дФ rc = R0 (ро) = ро + ;        0      2 Z (ро),

R ( Р , z ) = Р

1 +

др Р

V

(#

z

,

6 = ф ,

<

z c = ^Z 0 ^(р 0 ) ,

2^2/ X"1

1 - ( 7 И дФ J .

R ( р , z ) = -р

1+т

J1 V V

дФ 1 др Р

-(Ш

z

,

6 = П + ф .

Теперь рассмотрим уравнение луча

Якобиан преобразования в полярной системе координат имеет вид

1 ( д x₀ ( u , v ) д у 0 ( u , v ) д x 0 ( u , v ) д у 0 ( u , v )

J = р I др дф дф др

дФ r = R(р,z) = р+ /        -z ,

1 (дФ^

V1 -Ы

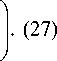
Используя выражения (23), в результате получаем:

где р - координата выхода луча.

Рассмотрим точку с координатами:

( r , ^z ) = ( R ' р 0 , Z 0 ( р 0 ) | ^{+ А} r , Z 0 ( р 0 ) ) .                ⁽³⁴⁾

J ( р, z ) =

R ( р, z ) д R ( р, z ) р      ^др

Подставляя (34) в уравнение луча (33), получаем другое уравнение

где R ( р , z ) имеет вид

R ( р 0 , Z 0 ( р 0 ) 7 + A r = R ( р, Z 0 ( р 0 ) 7 .                   (35)

R ( р , z ) = ±р

1+т

V V

дФ 1 др р

_(дФУ ( др)

z 2

.

Рассмотрим теперь случ ай, когда якобиан лучевого преобразования обращается в ноль. В этих точках пространства интенсивность в приближении геометрической оптики соответствует каустикам (равна бесконечности). Параметрическое уравнение поверхности, в которой якобиан обращается в ноль, имеет вид

r c ( р ) = р^-

(

1 -

V

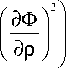
дФ (д ² Ф 1

др Vдр 2 J ’

(

1 -

. .        2         . Л-¹

' дФ | ' д Ф | V др J 7 V др ² J

Пусть эйкональная функция в плоскости z =0 имеет вид Ф ( р ) = а р⁷ [11, 12]. В этом случае параметриче-

ские уравнения каустик имеет вид:

r c ( р ) = р^-

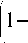
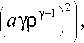
zс

',                    1 ²

^{1 -} ( ^а YР^Y 77 a Y ( Y- 1 ) р^7- 2

2.2. Определение координат двух лучей, приходящих вблизи каустики

Получим параметры лучей, проходящих вблизи каустики. Параметрические уравнения для каустики (30) можно переписать в виде

Из этого уравнения найдём точку выхода луча

Ar = R'р, Z0 (р0)J - R (р0, Z0 (р0)J = дR 7ро, Z0 (ро)J/        \

=               7 (р-р0) + др

1 ^д R 7^р0’ Z 0 ^(ро)7 /        \2

⁺ Т----⁷ ( р^-р 0 ) .

2 др

Так как на каустике дR (р0, Z0 (р0)7 = 0

др ,

1 ^д 2 R ⁽р 0 , Z 0 ( р 0 ) V       2

то ^A r = 2---- ⁷ ( р^-р 0 ) .

После преобразований получаем:

р = р 0 ±

1 ^д R ' ^р 0 , Z 0 ^(р 0 ) 7

2 д Т    др

V            г 7

.

В результате получаем координаты двух точек, лучи из которых приходят в заданную точку вблизи каустики.

2.3. Расчёт интенсивности в радиально-симметричном случае в рамках геометрической оптики

Выражение для интенсивности имеет вид

I ( x , у , z ) =

= J 1 0 ( x , у ) 8 ( x - x 0 ( u , v ) , у - у 0 ( u , v ) ) d u d v .

Переходя в области интегрирования и области наблюдения в полярные координаты, получаем выражение для интенсивности в цилиндрической системе координат.

С учётом различия двух случаев распределение интенсивности имеет следующий вид:

I ( г , ^z ) =

J"IOr^)5^r- r0(P,z)]Л1 (p)pdP, r0(P,z) > °’ = < 0 V2no j“Ш)^r + rO(P,z)]Л2 (p)p dP, rO(P,z) < 0, 0 у2по

Получаем на каустике:

5 "( p 0 ) = ( d R ( p 0 ) /d p ) 2 .                               (51)

Окончательно получаем

I ( r ) = ( d R ( p 0 ) /d p ) 1 1 0 ( p 0 ) Л ( р 0 ) p 0 , r = R ( p 0 ) . (52)

Следует отметить, что уравнение dR (Pc)/dp = 0                                     (53)

где I o ( p ) — входная интенсивность,

Г , (P , z ) = P + ( Ф р ( p )/>/1 -Ф р ( Р )) z ,

1 2 п I 2 r                 [ ф 11

^Л 1 ( Р ) = -/г=- I exp 1 2 r o ⁽ P , ^{z )sin} ШТ^d Ф ,

V 2 по ^J₀     [ о            V 2 ) J

1 2 п

I 2 r                  [ ф 11

^Л 2 ( P ) = ^^ I exP 1 — r M z ^)c0S I   |T ^d ф .

V 2 по ^J₀     [ о            V 2 )J

Вычисление интегралов по угловой переменной

Для вычисления интегралов по угловой переменной необходимо рассмотреть вычисление интеграла вида

2 п 1       I     X       [ ф 1 1

'H ^X ) ⁼ L ^_exp |-- 2 sin I   II ^d Ф              ⁽⁴⁴⁾

⁰ о     l о      V 2 ))

или

^{2 п} 1        | X 2 [ ф | |

Ф x = exp---cos      d ф .

-0 о l о ²       l 2 ))

При малых о этот интеграл можно вычислить методом Лапласа или методом перевала. Это предположение основано на том, что в окрестности нуля мож-

но использовать разложение в ряд Тейлора sin² ( ф /2 ) = ф ²/4.

С другой стороны, в окрестности ф = п cos² ( ф /2 ) = ( ф-п ) 2 /4 .

В результате всё можно свести к интегралу Пуассона.

Вычисление поля вблизи каустики в радиально-симметричном случае

Рассмотрим вычисление поля вблизи каустической поверхности в виде:

I ^{( r} ) =Г ^{1 0} ? ^ ) exp I^- ;12 ^{5 (p) 1 Л} ( ^{p)p d p , 0} 72по   V о )

где 5 ( р ) = 0,5 [ r - R ( р ) ] 2 .

Рассмотрим вычисление интеграла с помощью асимптотического метода Лапласа. Согласно методу Лапласа:

I ( r ) = ( 1 0 ( р 0 ) /V ⁵ "( р 0 ) ) Л ( р 0 ) р 0 , r = R ( р 0 ) .     (49)

Вычислив

5 '( р ) = - ( r - R ( р ) ) (d R ( р ) /d p ),

2                               (50)

5 "( р ) = ( d R ( р ) /d p ) + ( r - R ( р ) ) (d² R ( p ) /d p ²).

определяет каустику.

3. Численное моделирование для обобщённой линзы

В параграфе рассмотрено моделирование для эй-кональной функции, соответствующей обобщенной линзе [11, 12] вида Ф ( p ) = a p^Y .

На рис. 1 показаны графики каустик r c ( z c ), вычисленных по параметрическому представлению (31) для различных значений параметров a и у. На рис. 2-4 показаны результаты расчёта интенсивности по формуле (41) для рассматриваемой обобщённой линзы с теми же параметрами при равномерной входной интенсивности.

Рис. 1. Графики каустик для у = 2, a = - 0,005 (точечная линия), Y = 3, a = - 0,001 (пунктирная линия), Y = 1,5, a = - 0,05 (сплошнаялиния)

б)

Рис. 2. Распределение интенсивности (негатив) для y = 2, a = -0,005: продольное (x e [-100, 100],z e [-0,1, 120]) распределение интенсивности (а) и топологии (б) и поперечное (x^ye^-100, 100], z=10) распределение интенсивности (в)

Как видно из рис. 1 и рис. 2, при значении параметра у =2 (точечная линия) каустика выглядит как классический «ласточкин хвост». При увеличении параметра у =3 функция каустики становится более резко выгнутой (рис. 1: пунктирная линия, рис. 3).

Таким образом, для параметра у> 2 каустика имеет вид вогнутой функции. Если же 1 <  у <2, например, у =1,5 (рис. 1, сплошная линия), то функция имеет две каустические линии – выпуклую и линейную.

Рис. 3. Распределение интенсивности (негатив) для у = 3, a = - 0,001: продольное (x e [-100, 100], Z e [-0,1, 120]) распределение интенсивности (а) и топологии (б) и поперечное (x, y e [-20, 20], z = 10) распределение интенсивности (в)

а)

б)

в)

Рис. 4. Распределение интенсивности (негатив) для у = 1,5, a = - 0,05: продольное (x e [-100, 100], z e [-0,1, 120]) распределение интенсивности (а) и топологии (б) и поперечное (x, y e [-100, 100], z=10) распределение интенсивности (в)

Однако в задачах фокусировки излучения в глубине некоторого объёма, где актуально формирование резкого фокуса на некотором расстоянии от поверхности [13, 14], желательно иметь выпуклую каустику. Чтобы сделать её ярче, возьмём смещённую из центра эйкональную функцию Ф(p) = а(p-5)Y [15] (рис. 5), а чтобы убрать центральный пик, осветим эту линзу не плоским, а кольцевым пучком (рис. 6).

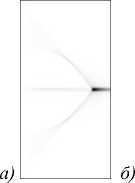
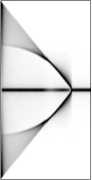
Рис. 5. Распределение интенсивности (негатив) для у = 1,5, а = - 0,05, 5 = 50: продольное (x e [-100, 100], z e [-0,1, 200]) распределение интенсивности (а) и топологии (б) и поперечное (x, y e [-50, 50], z=100) распределение интенсивности (в)

• 4.    Формирование каустик гармоническими оптическими элементами

в радиально-симметричном случае

Пусть на эту линзу падает плоский пучок немонохроматического света с длинами волн в интервале % 1 <  % <  % 2 . Оценим размеры функции рассеяния точки в зависимости от длины волны.

Будем считать, что дифракционный элемент изготовлен в виде гармонической линзы [8-10] с высотой рельефа %N для базовой длины волны %0. Такой оп- тический элемент можно локально представить в виде дифракционной решётки с периодом [16]:

d = (%0 N )/(dФ (p)/dp),(54)

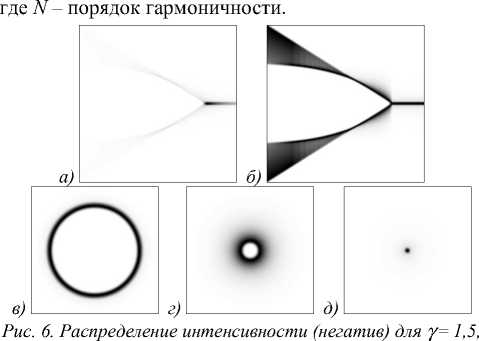
а = - 0,05, 5 = 50 при освещении кольцевым пучком: продольное (x e [-100, 100], z e [-0,1, 200]) распределение интенсивности (а) и топологии (б) и поперечные распределения интенсивности (x,y e [-50, 50]) при z=100 (в), z=150 (г), z=200 (д)

Луч, падающий параллельно оптической оси, при попадании на эту дифракционную решётку отклоняется. Наклон луча а к оптической оси равен

а(%) = m (%/ d),(55)

где m - порядок дифракции.

Подставляя выражение (54) в (55), получаем

а(%) = (%/%0) (m /N) (dФ(p) /dp).(56)

Приведённая формула означает, что гармонический ДОЭ на заданной длине волны порождает несколько волновых фронтов. Каждый волновой фронт эквивалентен волновому фронту, который создаёт ДОЭ с эйкональной функцией

* mN ( р , % ) = ( % / % 0 ) ( m / N ) Ф ( p ) .               (57)

В результате выражение для интенсивности имеет вид:

N

I n ( r , z , % ) = Z T m , N ( % ) LN ( Г , Z , % ),              (58)

m=-N где

I m , N ⁽ r , ^Z , % ) =

J i 0 ( p ) S [ r - r ), m,N ( p , Z , % ) ] Л ,^, N ( p , % ) p d p ,

= _t       Г 0,m,N ( p , Z , % ) >  0;                             (59)

J I 0 ( p ) 8 [ Г + r_Q _ m , n ( p , Z , % ) ] ^Л 2, m , n ( p , % ) p ^d p , ⁰

r 0, m , N ⁽ p , ^Z , % ) <  ⁰ ;

r 0, m , N ⁽ p , Z , % ) = p + ^T m , N ( p , % ) ^1 ^{- [T} m , N ( p , % ) ] ² Z , ⁽⁶⁰⁾

Λ1,m,N(ρ,λ)=1/ 2πσ× xj exp{-(2r/а2)r,,.,w(p,z,X)sm2 (^/2)}dф,

Λ2,m,N(ρ,λ)=1/ 2πσ× xj = exp{(2rZo2)r,.. n(p,z,X)cos2 (ф/2)}dф,

T ., (M = Sinc² [« ( I , N Г К- m ) ] ,

T m , n ( λ ) – коэффициент пропускания гармонического ДОЭ. Анализ выражения показывает, что гармонический ДОЭ генерирует множество каустик.

На рис. 7 и 8 показаны результаты моделирования для параболической гармонической линзы γ =2, a = - 0,005 (с фокусным расстоянием f = 100) при учёте трёх дифракционных порядков. Базовая длина волны была выбрана λ 0 =633 нм. Рассмотрены три случая: 1) длина волны освещающего излучения совпадает с базовой длиной волны λ = 633 нм; 2) меньше базовой λ =532 нм; 3) больше базовой λ =750 нм.

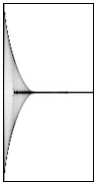
а)

б)

в)

Рис. 7. Распределение интенсивности (негатив) для гармонической линзы γ = 2, a = - 0,005, λ 0 = 633 нм: продольное (x ∈ [–100, 100], z ∈ [–0,1, 300]) распределение интенсивности (а) и топологии (б) и поперечное (x, y ∈ [–10, 10], z = 100) распределение интенсивности (в): для λ = 633 нм (верхняя строка), для λ = 532 нм (средняя строка), для λ = 750 нм (нижняя строка)

Заключение

В статье описан новый подход к расчёту распределений световых полей в рамках геометрической оптики. Предложен новый интегральный оператор для вычисления распределения интенсивности в рамках геометрической оптики.

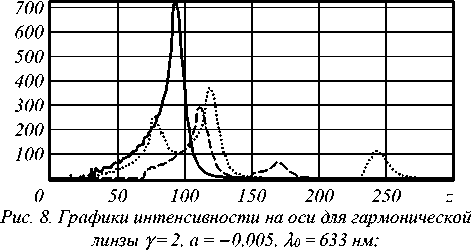
при λ = 633 нм (сплошная линия), λ = 532 нм (точечная линия), λ = 750 нм (пунктирная линия)

В рамках предложенного метода найдены распределения интенсивности от ранее изученных волновых фронтов, в частности, параболического, кубического и также волнового фронта, который описывается дробной степенью от радиуса. Найдены особые точки этих распределений, и рассчитаны распределения интенсивности вблизи каустик.

В дальнейшем планируется провести аналогичные исследования с использованием интеграла Кирхгофа, в том числе с учетом векторного характера полей.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант 16-29-11744 офи_м).