Гидравлическое давление при валковом отжиме

DOI:

В процессе валкового отжима мокрых материалов наблюдается одновременное происхождение двух явлений ‒ контактное взаимодействие и фильтрация влаги. При этом изменение показателей контактного взаимодействия влияет на изменение фильтрация влаги, и наоборот. Поэтому исследование одного из явлений без учета другого не позволяет получить достоверные параметры процесса валкового отжима мокрых материалов. Соответственно, для описания валкового отжима мокрых материалов необходимо совместное решения двух задач: первая ‒ контактное взаимодействие в двухвалковых модулях (контактная задача); вторая ‒ фильтрация влаги в деформируемой неоднородной пористой среде (гидравлическая задача).

К исследованию явления контактного взаимодействия при валковом отжиме мокрых материалов посвящены работы [1-4]. В них разработаны математические модели формы кривых контакта валков, напряжений трения и распределения контактных напряжений в обобщенном двухвалковом модуле.

Одной из основных гидравлических задач теории валкового отжима волокнистых материалов является задача моделирование распределения гидравлического давления в области отжима [5].

Анализ работ, посвященных к исследованию гидравлических задач валкового отжима мокрых материалов [6-11], показал, что существующие модели распределения гидравлического давления в области отжима получены с введением моделей валкового оборудования и материалов, не отвечающих реальным физическим явлениям валкового отжима мокрых материалов. Следовательно, существующие модели распределения гидравлического давления не дают возможности корректно раскрыть гидравлического явления валкового отжима мокрых материалов.

В работе [12] были определены аналитические зависимости, описывающие закономерности распределения гидравлического давления в области отжима для симметричного двухвалкового модуля.

В целях дальнейшего развития теоретических представлений в работах [1,4] объектом исследования служит обобщенный двухвалковый модуль (рисунок 1).

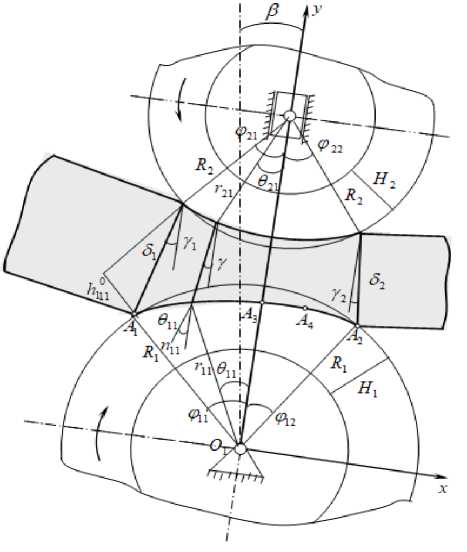
Рисунок 1. Схема двухвалкового модуля отжимных машин.

Figure 1. Scheme of a two-roll module pressing machines.

В данной модели валки расположены относительно вертикали с наклоном справа под углом β , имеют неравные диаметры с эластичными покрытиями ( D ≠ D ) , слой мокрого (обрабатываемого) материала имеет равномерную толщину δ и подан с наклоном вниз относительно линии центров под углом γ .

МЕТОДЫ

Кривая контакта нижнего валка (кривая A 1 A 2 ) состоит из двух зон A A и A A .

В зоне Л1Л3 происходит сжатие волокнистого материала и покрытия валка, а A3 А2 - зона восстановление деформации.

Сначала рассмотрим процесс фильтрации жидкости в зоне A A .

Уравнения кривой контакта нижнего валка в зоне сжатия для рассматриваемого двухвалкового модуля имеет вид [1]:

^r 11

f 1 + к ' C*n± Z 1) J

1 + к 11 ' 11 (     ^{11 11} cos( 9 _u + Y ) ^J

^{- (} Ф 11 ⁺ Y 1 ) ^ 9 11 ⁺ Y ^ 0,

mWH 1 ^Si n( Ф 11 ⁺ Ф 21 )      _A 1’1 m n( ^A / ц) ср ^{- ( A} _n ^{(1 -} m J^- A V^{1 -} m^)hV

, '' 1                                                                                                  ;

m ^ sin( ^ 21 - Y 1 )         Ац m 11 ⁽ A У ср ^{+ (} A 11 ^{(1 - m} _n) ^- A 11 ^{(1 -} m J) H 1

о     ^sin( Ф 21 ^- Y 1 ) ,               ^f   sm^ ⁺ Y 1 ) )

^h11 ^{— 5} 1   —,—;;   ^{( A /} ц) ср ^— R 1 ■ ¹ —>

Sin(^11 + ф 21)                  (     2(^n + Y1) J здесь mx t - коэффициент упрочнения точек эластичного покрытия нижнего валка при сжатии, mj - коэффициент упрочнения точек мокрого материла при сжатии.

Откуда

_ к ЦАЦ R1        sin би

^r 11 =             ^cos Ф 11      _г „ .

1 + к ₁₁ ' ₁₁        cos 9_n

В зоне A A волокнистый материал сжимается, поэтому жидкость переходит из нее в покрытие валка вдоль полярного угла [8,12].

Процесс течения жидкости будем считать сплошным и установившимся.

Скорость волокнистого материала в области контакта, величина постоянная и равна v _m .

Скорость жидкости в области контакта – величина переменная и равна [8]:

u 11 9 =^{- Ь}11⁽⁽ Ф 11 ⁺ Y 1 ) 3 ^{+ ( 9} 11 ⁺ Y ⁾³⁾ , ^{- (} Ф 11 ⁺ Y 1 ) ^ ⁹ п ⁺ Y ^ ⁰ ,               ⁽³⁾

где b ₁₁

V m^R 1^cos( ф 11 ⁺ Y 1 )                _Ло        ^s ln( ф . _| ^- Y 1 )

о                                                    , ^h11 — ^ 1                      ‘

3 h 11 (1 + к 11 ^A 11 )(1 + к 11 ' 11 cos( ф 11 + Y 1 ))              ^sin( Ф 11 ⁺ Ф 21 )

В работе [5], принимая рабочую гипотезу об ортогональности максимальной и минимальной пористости, установлена применимость для анизотропной среды обобщенного закона Дарси дPn _    u9

и , dn       Kfl с коэффициентом фильтрации

22 cos a sin а

+

К    КК .

• v a      v max

где p, ue - гидравлическое давление и скорость фильтрации в направлении n; и - коэффициент вязкости жидкости; Kmaх - максимальный коэффициент фильтрации по направлению поперек поверхности материала (по оси Оу); Кть - минимальный коэффициент фильтрации по направлению вдоль нитей основы материала (по оси Оx).

Согласно этой зависимости, угол направления фильтрации меняется в пределах 0 < a < 90 o. На валковых отжимных машинах, где валки имеют эластичное покрытие, в каждой точке кривой контакта валка результирующая скорость фильтрации будет направлена по отношению к направлению движения материала под некоторым углом

90 o —

• a , близким к полярному углу Q [2]. Поэтому для этого случая можно принять

90 o — a = Q [12]. Тогда выражение коэффициента фильтрации примет вид:

1 sin² Q cos² Q

.

-----=--1--

K Q    K max    K min

Согласно формулам (3), (4) и (5), находим dPn=ubii d n ii

^{Sln Q + у} ) + ^{cos Q + у} )

К

V    ^iimax

к iimin    7

(( ^ 11 + Y i ) + ( Qu + У)^

или приняв COS 2 ( Q ] + у ) « 1 — ( Q , + у ) 2

и ^sin^{2( Q} _n + у ) « ^{( Q} _n + у ⁾²

^dPii n        ^{U b}ii

d ( Q ii + у ) K iimin V

i--Ihnax

—

^K 11min

K 11max

( Q ii + у )² ! (( ^ ii + у )³ + ( Q ii + у )³) 7

dn ₁₁

^{d ( Q} ii + у )

.

Из рисунка 1 следует, что n_x j = r_x j cos( Q _n + у ) .

Отсюда находим dn

—- = r ii ^{cos( Q} ii + у ) ^{— r} ii ^{sin( Q} ii + у ) d (Q, + у )

или с учетом равенства (1) и (2) dn ₁₁

-

R 1

d (Q_x + у ) i + k_x ^_x

- sin( Q _H + у )

-

R r"h(Qii+у ).

^{1 + k} 11

Учитывая это, из равенства (6) получим dP11n

^

^{u R}i b ii

d ( Q u + у )    (i + k „Я н) K ,

f

—¹ iimin V

^

^K 11max

^

K 11min

K 11max

\

( Q ii + у )²  (( ^ _n + у 1 )³ + ( Q ii + у ) ³ )( Q ii

⁺ У )

или, ограничиваясь членами до третьей степени относительно Q t + у), получаем dPiin =

^{u R} i Ьц⁽ Ф 11 + у 1 ^{) 3 f}

K 11max

^

^K 11min

(i + k ii ^ ii ) K „mm V

^K 11max

( Q ii + у ) ³ — ( Q u + у ) 1 d ( Q u + у ).

После интегрирования получим

Современные инновации, системы и технологии // Modern Innovations, Systems and Technologies 2023; 3(1)

(

P 11 n = d -11^—1^ ( 9_И + Y ) ⁴ - 2(^ 911 + Y ) ² I + C 11 ,

V    — 11max где с11

U v m R ^COs( Ф 11 ⁺ ЛХ ф ц ⁺ Y 1 ) 3

12 - 11m _in h °(1 + k n Z n)(1 + k 11 ^ 11 cos( ^ 11 + Y 1 )) .

Постоянную C! находим по начальному условию р ,_n ( - ф [ + Y i )) = 0 :

(           .  -..

C _n = 2(фц + Y v? - -1^--- m ф + Y 1 ) 4 .

V                    — 11max

Тогда имеем

<.^

P11 n = c 1Ж1 + Y1)2 -(911 + Y)2) 2--11max----2m"(ф + Y1)2 + (911 + Y)2) ,

V        — 11max где  - (Ф11 + Y1) < 911 + Y < 0.

Эта формула определяет закономерности распределения гидравлического давления по кривой контакта нижнего валка в зоне сжатия.

Закономерности распределения гидравлического давления по кривой контакта нижнего валка в зоне восстановления деформации определяем аналогично:

P2. = c 12«P14 + Y4)2 -(912 + Y)=)f2-- 12m""- 12mln (Ф + Y4)2 + (912 + Y)2)1

V        —12 max где 0 < 9 2 + Y < Ф12 + Y2;  ^14 + Y4 = 51(Ф12 + Y2), 0 < 51^ с12

^{U V} m ^R 1 ² C0S⁽ ^ 1 ₂ + Y 2 ⁾⁽ ^ 12 ⁺ Y 2 ⁾³

12 - 12min ^ 102 (1 + k 12 ^ 12 )(1 + k 12 ^ 12 ™^12 + Y 2 )) ^.

Аналогично находим закономерности распределения гидравлического давления по кривой контакта верхнего валка.

Они имеют вид:

P21 n = c21((Ф21 -Y1)2 -(921 -Y)2)f-21m:x  -21mln ((Ф21 -Y1)2 + («21 + Y)2)-2],

V    — 21max где

^{- (} ^ 21 ^- Y 1 ) <  ⁹ 21 ^- Y <  ⁰ ,

12 - 21min h 01 (1 + k 21 ^ 21 )(1 + k 21 ^ 21 G0S( ^ 21 - Y 1 )) ’

P22 n = c 22«P 24 - Z4)2 - (922 - Y) 2 )| - 22m1.'  - “mi" ((ф 24 - T 4V + (922 - Y )2) - 2 ]■

V    - 22max где 0 < 922 -Y < Ф22 -Y2; ф- Y4 = 52(ф22 -Y2), 0 < 52 < 1;

υ v_m R ₂² cos( ϕ ₂₂ - γ ₂)( ϕ ₂₂ - γ ₂)³ 12 K 22min h 2 ⁰ 2 (1 + k 22 λ 22 )(1 + k 22 λ 22 cos( ϕ 22 - γ 2 )) ^.

РЕЗУЛЬТАТЫ

Определены аналитические зависимости (9)-(12), описывающие закономерности распределения гидравлического давления в зоне отжима для обобщенного двухвалкового модуля, представленного на рисунке 1.

Графики изменения гидравлического давления по кривой контакта валков приведены на рисунке 2.

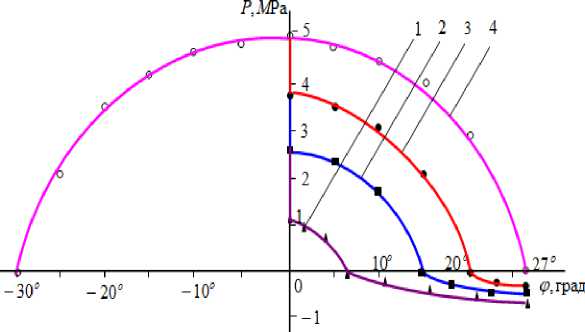
Рисунок 2. Графики изменения гидравлического давления по кривой контакта валков:

1                       1                      3

1 ^^4 ~ 4 ^'²* 2 ^_^4 ⁼ *ЧЧъ 3-^4 ⁼ 4 Й2> 4-^4 = ^|₂.

Figure 2. Graphs of changes in hydraulic pressure along the roll contact curve.

ВЫВОДЫ

• 1.    Разработаны математические модели распределения гидравлического давления в зоне отжима.

• 2.    Из анализа расчетных данных и графиков следует, что гидравлическое давления в зоне сжатия увеличивается от нуля в начальной точке контакта до максимума в точке, лежащей на линии центров. Закономерности распределения гидравлического давления в зоне восстановления деформации

зависят от протяженности ее части, где жидкость переходит из мокрого материала в покрытие валков.