Гидродинамическая смазка радиального подшипника повышенной несущей способности, обусловленной профилем его опорной поверхности и шероховатостью поверхности вала

Исследованию влияния одномерной шероховатости поверхности на несжимаемую гидродинамическую смазку посвящено большое количество работ. Общее признание получила теория Кристенсена и Тондера [1,2], дающая усредненное описание такого влияния для опор (подшипников), использующих в качестве смазки несжимаемую жидкость. В указанных работах не исследованы вопросы прогнозирования оптимальной по несущей способности формы опорной поверхности. В них только лишь установлено, что путем варьирования значений характеристик движущейся шероховатой поверхности можно обеспечить повышенную несущую способность подшипника.

Постановка задачи. Рассматривается установившееся движение смазки в зазоре радиального подшипника, близкого к круговому, который предполагается неподвижным, а шип с шероховатой поверхностью движется вокруг своей оси с угловой скоростью 6. Пространство между шипом и подшипником заполнено вязкой несжимаемой жидкостью. Уравнения контуров вкладыша и шипа в полярной системе координат (r‘, 9) с полюсом в центре шипа можно записать в виде r ' = r1 + e cosG - A sin toG, r ' = r0 - A sin 69. (1)

Здесь r ₀ и ситет;

r ₁ соответственно радиусы кругового вала и кругового подшипника; е - эксцентри- А и ω - амплитуда и частота контурных возмущений на поверхности подшипника;

А и ω - амплитуда и частота контурных возмущений на поверхности шипа.

еAA

— = n < 1, — = П < 1, — = £ << 1, о = r - r .

δ ^, δ ^{1     ,} δ ^{,        1    0}

В качестве исходных уравнений берется следующая безразмерная система уравнений «тонкого слоя» для вязкой несжимаемой жидкости:

8 ² u _ dp 8T6 = d9 ’

8 u 8 u .

— + — = 0.

8 r   8 9

Здесь размерные величины r ', u ', u ', p' связаны с безразмерными r , u,u,p соотношениями:

*     * Ptor r = r0 + or; и = toou; u = toru; p = p p, p = —^0-0                                  0                           o2

•

где u', U - компоненты вектора скорости; р^r - гидродинамическое давление; ц ский коэффициент вязкости.

Система уравнений (3) решается при следующих граничных условиях u = 0, и = 0 при r = 1 + ncos0 — П1 sin®0 = h(0);

u = 1, и = 0 при r = — e sin to*0 ; p (0) = p (2 п )•

Граничные условия на поверхности вала можно записать в виде:

— динамиче-

u(0,-esinto 0) = u(0,0)--0£srnю 0 + dr'r=0

u (0, - e sin to 0 ) = u (0, 0 )-- L_₀ £ sin to 0 + .

a r i ' =0

• ••

• ••

= 1,

= 0.

С учетом (6) решение задачи (3) – (5) будем искать в виде рядов по степеням малого параметра ε :

w

u = Z ue, k=0

w k=0

w p=E Pkek • k=0

Подставляя (7) в (3) и (5) и сравнивая коэффициенты при одинаковых степенях ε с точ-

ностью до членов 0( e ²) , будем иметь:

d2 u 0   dp 0"d^ " d0 ’

^{d u} .- ^u = 0; d r    d 0

u 0 = 0, u = 0 при r = h (0 ); p 0 (0) = p 0 (2 n );

u ₀ = 1, u ₀ = 0 при r = sin to '0 ;

—= —, —1 + —1 = 0;

u1 = 0, u1 = 0 при r = h(0); p1(0) = p1(2n), u1 |r=0 =du°|r=0sin Ю0, U1 |r=0 =dUL |r=0sin Ю0.

d r                      d r

Решение задачи для нулевого (8) – (9) будем искать в виде [3-5]:

^u о =^ ^ 0 + ^U o^{( r, 0} ); u d r

приближения. Точное автомодельное решение

задачи

0 =

—

V +

U о = u o ( ^ ); V о = U o (^)h00 );

V ( r ,0 ); dp 0 = c¹^. + cl^tl ; ⁰           d0 h ²( 0 ) h ³( 0 )

^ = r I h ^{( 0} );   v 0 = ^V 0^{( f} )•

Подставив (12) в (8)и (9), получим:

V 0 = с 2,   ¹

V 0 (0) = V 0 (1) = 0;

u^0 = 1,

U 0 — ^u 0 = 0;

u ₀ = 0 при £ = 0;

й₀ = o, u _o = o при 5 = 1; J u₀(5 ) d5 = 0; p (0) = p (2 n ).

Решение задачи (13) – (14) находится непосредственным интегрированием. В результате будем иметь:

V 0 = ^c ₂ ( 5 ² - 5 ) ,

-

u O ^C 1

0     1 2

с1ξ2  ξ2

-

—

/ ~    X

k7 +1 5 + 1, к2   J

C 1 = 6.

Гидродинамическое давление р0 определяется из уравнения где

с 2 =

dp o = dθ

~

^“1

■ ^c 1 1 +

C2

h ² ( θ ) h ³( θ )

~ ~

Перейдем к определению поддерживающей силы. Для безразмерных компонент R и R xy вектора поддерживающей силы и безразмерной силы трения Lтр в принятом нами приближении получим следующие выражения:

R y

R y r ₀ p

2 π

J - p ⁰ cos9 d 9 = 6nn - 3 n 1

L тр

R x

—~ = ³ П 1

r 0 p

1 - cos(ro + 1)2п 1 - cos( ro - 1)2 п

го + 1

+

ro - 1

;

sin( го - 1)2 п   sin( ro + 1)2 п

-

ro - 1

го + 1

;

Lδ тр µωr ₀

2 π

₌ f V o

J h²

к h

+ u ⁰

h J

I , =0 d9 = - 2 п + — (cos2 nro - 1). ω

Перейдем к решению задачи (10) – (11).

С учетом (11) и (15) решение этой задачи запишется в виде u1

-

rh 2

л

+

J

c 1

—V + 4-

2 h ²     h

-

r sin ro 9 + —sin ro 9 .

h

Проинтегрировав второе уравнение системы (10) по r от 0 до h ( θ ) для определения родинамического давления p 1 , приходим к следующему уравнению:

гид-

-

h ³ dp 1 c ₂sin го 9

-

12 dθ

4 h

- 2sin ro 9 = Q 1 .

Здесь Q 1 – добавочный расход, обусловленный шероховатостью поверхности вала. Используя граничные условия р 1 (0) = р 1 (2 π ) для Q 1 , получим следующее выражение:

₁₂ Q = -3 c 2 J 4 (2 n )

¹      J ₃(2 π )

—

~

₂₄ J ₃ (2 π )

J ₃(2 π )

.

^{2 π} sin ω ^* θ              ^{2 π} d θ

.

Здесь J, (2 n ) =  —г---- d 9 , J, (2 п ) = —г---

" J h^k(9 )          k J h^k(9 )

С учетом (20) для определения гидродинамического давления приходим к следующему уравнению:

dp1 dθ

^3c 2 ^J 4 ⁽²ⁿ⁾ + 24 J 3 ⁽²ⁿ)

J3(2π)h3      J3(2π)h3

—

* 3c₂ sinωθ

h4

—

24 sinω^*θ h³

.

Для безразмерных добавочных компонент поддерживающей силы будем иметь:

-—^

R yд об

R yд об

* r₀ p

2π

ч

^p cosθdθ; dθ

.—^

R x д об

R xд об

* r₀ p

2π

-J

^p sinθdθ.

dθ

С точностью до членов 0(εη), 0(εη₁ ) для R yд_об и R xд_об получим:

~

^Ryd o6 ^{- 3}

cos(to - 1 )2п - 1 , cos(to + 1 )2п - 1

* i                   1                       *        , to -1                to +1

~

R x^d₀ 6 ^{- 3}

sin( to - 1 )2 n sin( to + 1 )2 n

** to — 1             to + 1

В принятом нами приближении добавочная сила трения, обусловленная наличием шероховатости поверхности вала, определяется выражением

Lmp.g06 = to2*"(cos2nto - 1).

Таким образом, для безразмерных составляющих несущей способности и безразмерной силы трения окончательно получим:

^   ^        ^^

Ry - Ry + SRydoS ; Rx - Rx + ERxdo6 ; Lmp, - LmP + GLmpdo6 , где Rx,Ry,Lтр определяются формулами (18), а Ryдоб ,Rxдоб ,Lтр доб определяются форму- лами (23) и (24).

сущей способности показывают:

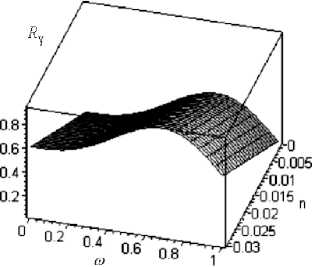
Зависимость безразмерной R y составляющей несущей способности от параметров η и ω

Выводы. Результаты численного анализа полученного аналитического выражения (25) для не-

• 1.    При £ • to - 0,002, to - 1/2, n - П предложенная конструкция подшипника обеспечивает двукратно повышенную его несущую способность по сравнению со случаем, когда to - 0 (рисунок).

• 2.    При n _- n ₁, _{to -} ¹ , варьируя характеристики микронеровностей ( £ и to ) поверхности вала, можно обеспечить еще более повышенную несущую способность подшипника. Заключение. Полученные в работе результаты позволяют разработать конструкцию радиального подшипника, который выдерживает максимальную нагрузку при заданных его размерах.