Гидродинамические неустойчивости в тахоклине, обусловленные вариациями толщины слоя

Одной из важных задач физики Солнца является исследование закономерностей возникновения и динамики крупномасштабных магнитных полей. Многие из особенностей крупномасштабных магнитных полей могут формироваться в тахоклине – тонком слое под конвективной оболочкой с большими вертикальными градиентами скорости дифференциального вращения. Определение роли тахоклина в формировании различных проявлений солнечной активности представляет собой одну из актуальных проблем солнечной физики. В работе [Tikhomolov, Mordvinov, 1996] предложена гипотеза, объясняющая формирование в верхней части тахоклина, названной активным переходным слоем (АПС), крупномасштабных гидродинамических структур, проявлением которых в фотосфере могут быть комплексы активности или крупномасштабные области фонового поля. Образование в слое проникающей конвекции долгоживущих гидродинамических структур способствует более эффективному перемешиванию плазмы в тахоклине, этим можно объяснить низкое содержание лития в солнечной атмосфере [Tikhomolov, 2005]. В работе [Zagarashvili, et al., 2010] показано, что в тахоклине могут развиваться колебания типа волн Россби–Альфвена, свойства которых могут быть связаны с колебаниями солнечной активности в фотосфере и короне в диапазоне периодов 155–160 сут. Юй-Цинь Лоу [Lou Yu-Qing, 2000] предположил, что различные типы экваториально захваченных волн Россби могут возникать в тонком подповерхностном слое плазмы.

Принципиальное значение для данных гипотез имеют механизмы развития неустойчивостей в тахоклине. Как показано в работах [Gilman, Fox, 1997; Cally, 2003; Dikpati, Gilman, 2005, 2007], важное значение для развития неустойчивостей имеет наличие в тонком слое жидкости тороидального магнитного поля. Однако если допустить возможность воз- никновения в АПС на границе между конвективной оболочкой и тахоклином крупномасштабных гидродинамических структур, как это предполагается в работе [Tikhomolov, Mordvinov, 1996], то эти образования могут служить дополнительным источником неустойчивостей в тахоклине. Энергия для развития неустойчивостей в этом случае будет черпаться из энергии среднего потока. Условием для развития неустойчивости будет различие скоростей потока в тахоклине и скорости вращения крупномасштабных гидродинамических структур.

Для оценки условий возникновения неустойчивостей принято использовать метод малых возмущений. Применение этого метода предполагает возможность выделения «среднего потока», удовлетворяющего стационарным уравнениям гидродинамики. Эта задача далеко не тривиальна, если течение сильно возмущено (пример – земная атмосфера) или испытывает сложные внешние воздействия. Появление долгоживущих гидродинамических структур в АПС должно изменять и горизонтальную, и вертикальную структуру потока в тахоклине. Учесть одновременно оба этих эффекта сложно, поэтому мы разделили задачу на две части:

• 1)    исследование влияния вариаций толщины слоя на устойчивость осесимметричного потока жидкости с дифференциальным вращением;

• 2)    исследование влияния на развитие неустойчивости отклонений структуры среднего потока от осевой симметрии. В представленной работе решается первая задача. Влияние магнитного поля на развитие неустойчивостей не учитывается.

Модель

Исследование проводилось с помощью численных экспериментов с баротропной дивергентной квазигеострофической гидродинамической моделью. Модель широко применяется в различных вариантах, начиная с исследований Гилмана в 60-х гг. прошлого века [Gilman, 1967]. Основой модели является уравнение квазигеострофического потен циального вихря в приближении «мелкой воды»:

8Av

8 ‘

1 8v 8Av a 2 _ 5ц 81

8v 8Av

81 8ц

x

2Q 8v x ---+ R — rAv, a2 81

где v — функция тока, R - источник завихренности, r – коэффициент релеевского трения, a – радиус Солнца, Q - угловая скорость вращения Солнца, 1 -долгота, ц=cos9, 9 - полярный угол.

После линеаризации относительно среднего поля скорости уравнение для возмущений функции тока v' принимает вид

8AV‘ + L (v', V)v' = R, (2)

где

-0  8v' ^8Av o

+

81 8ц

L - v ) =4 ^8V‘^1AV

a _ 8ц 81

8v 8Av' 8v 8Av‘ +

—

8ц 81   81 8ц _

2 Q 8v‘ . , —;— — Г Av' a ² 81

—

линейный дифференциальный оператор, зависящий от среднего поля скорости, определяемого функцией тока v .

Источник завихренности в правой части уравнения (2) характеризует влияние вариаций толщины слоя жидкости на динамику возмущений функции тока. Примем эту величину равной нулю и исследуем устойчивость дифференциального вращения без учета вариаций толщины слоя жидкости. При исследовании устойчивости классическим методом Ляпунова возмущение функции тока сводится к представлению в виде суммы нормальных мод:

v' ( 1, ц, ‘ ) = Re ] e ° ‘ ^ v _Y Y , ( ц, 1 )

I

= { v _Y =v _Y R ⁺ i v y I } = ^e ° ‘ E P rOO ^Re [ ( v y R ⁺ i v y I ) ^x (3)

Y

x ( cos m 1 + i sin m 1 ) ] =

= e ° ‘ E P y ( ц ) [ v y r ^co s ^m 1 - v y i sin m 1] ,

Y где ° - комплексная частота нормальной моды, y -комбинация индексов n и m, определяющих степень и порядок сферических функций Y,(ц, 1), по которым производилось разложение возмущений функции тока, PY(ц) - присоединенные полиномы Лежандра.

После подстановки (3) в исходное уравнение и интегрирования по сферической поверхности приходим к системе алгебраических уравнений относительно комплексных коэффициентов разложения v_Y и частоты колебаний ° . В матричном виде эту систему уравнений можно записать следующим образом:

Элементы матрицы A yy' представляют собой выражения

E vy J y * n ( n ⁺ 1 )v ^Y i y

8 Y --V v 8ц ⁿ

—

imY Y U n x

x dS — 5^ , _ i 2 Q m '/ n ( n + 1 ) + r ] ,

_ j8Av n (n + 1)8v]

n l^^^-             I ,

I 8ц      a 8ц I

- j8Av n (n +1) 8v n = |1T+

.

a ²    81

В случае зональной симметрии Vn = 0, что суще- ственно упрощает решение задачи.

Приведенная система уравнений служит для нахождения собственных чисел и собственных векторов матрицы A . Для решения этой системы использовалась стандартная процедура LA_EIGENPROBLEM языка программирования IDL. Для удобства представления результатов характерное время релеев-ского затухания было принято равным 1000 оборотов Солнца. Задание этой величины не очень важно, так как включение диссипации приводит всего лишь к сдвигу спектра нормальных мод вдоль действительной оси.

Профиль дифференциального вращения, определяющий среднюю функцию тока, был задан в форме, предложенной в работе [Kitchatinov, Rüdiger, 2009]:

Q = Q₀ ( 1 — a ( ( 1 — f ) cos² 9 + f cos⁴ 9 ) ) . (6)

Здесь Q ₀ - угловая скорость дифференциального вращения Солнца на экваторе, коэффициенты а и f характеризуют степень дифференциальности среднего потока.

Результаты

Для каждой комбинации параметров a и f , определяющих характер дифференциального вращения, были рассчитаны наборы собственных чисел и собственных векторов матрицы A . Затем были выделены наиболее неустойчивые моды, для которых были построены зависимости инкрементов роста и периодов колебаний от параметров дифференциального вращения a и f . Эти зависимости представлены на рис. 1 и 2.

На рис. 1 изображены распределения нормализованных скоростей роста наиболее неустойчивых мод °' =Re( ° )/ Q ₀. В левой нижней части рис. 1 значения инкрементов роста нормальных мод меньше нуля, эта часть плоскости соответствует устойчивому дифференциальному вращению. В правой верхней части рисунка инкременты роста нормальных мод положительны и возрастают с увеличением коэффициентов a и f . Сравнение с результатами расчетов, приведенными в работе [Kitchatinov, Rüdiger, 2009], показало, что по порядку величины рассчитанные инкременты близки скорости роста нормальных мод с зональным волновым числом m =1, рассчитанным с учетом вертикальной структуры возмущений, однако горизонтальная структура наиболее неустойчивых мод в наших расчетах оказалась более сложной, с преобладанием мелкомасштабной составляющей.

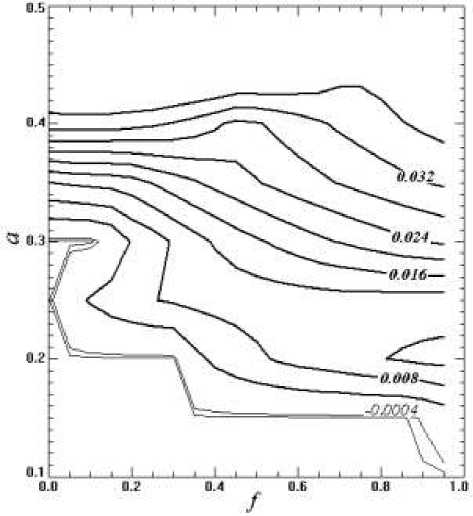
Рис. 1 . График зависимости нормализованных скоростей роста наиболее неустойчивых мод от коэффициентов a и f , характеризующих дифференциальное вращение.

0.(1 п.

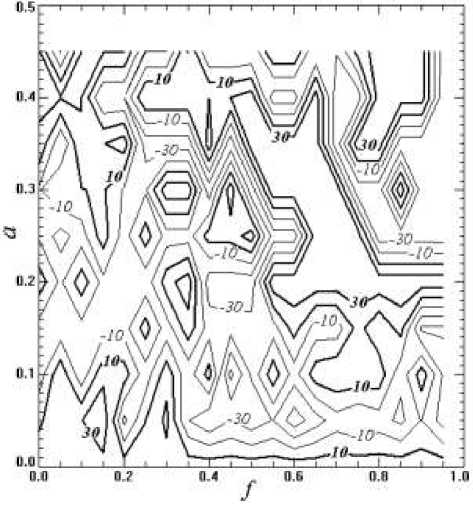
Рис. 2 . Периоды колебаний наиболее неустойчивых мод (единица измерения – 1 оборот Солнца). Толстые линии соответствуют движению нормальных мод в направлении вращения, тонкие – движению в противоположном направлении.

вращения и слабой неустойчивости. Наибольших значений периоды колебаний достигают при a ∼ 0.2– 0.4, f ∼ 0.5–0.8.

В целом результаты расчетов показали, что дифференциальное вращение Солнца достаточно стабильно при рассмотрении в широком диапазоне параметров. Поэтому гидродинамическими неустойчивостями зонально-симметричного потока сложно объяснить многообразие наблюдаемых на Солнце быстро протекающих явлений. Инкременты роста неустойчивостей оказываются для этого слишком малыми, а периоды колебаний в большинстве случаев слишком большими. Неустойчивости зональносимметричного потока возрастают при учете магнитного поля, однако можно предложить и другой вариант возникновения возмущений – это деформация горизонтальной и вертикальной структуры среднего потока. И то, и другое может быть следствием особенностей МГД-процессов на границе между конвективной оболочкой и тахоклином. При этом средняя зональная составляющая в распределении поля скорости может оставаться в области устойчивости. Можно провести аналогию с процессами в атмосфере Земли. Хорошо известно, насколько динамичными являются синоптические процессы в тропосфере. Характерное время генерации вихрей составляет около 7 сут. Между тем, если мы оценим степень неустойчивости средней зональной составляющей потока, она окажется невысокой, а типичное время развития неустойчивостей составит порядка месяца. Возможно, и под конвективной оболочкой Солнца сложные динамичные процессы находятся в равновесии с достаточно устойчивым дифференциальным вращением. Глобальная гелиосейсмология, использующая процедуры пространственного и временного усреднения, в принципе не может выделить эти особенности.

Перейдем к решению задачи оценки влияния на устойчивость дифференциального вращения вариаций толщины слоя тахоклина. Так как метод нормальных мод в данном случае неприменим, мы воспользовались для оценки роста возмущений со временем спектральным методом численного интегрирования уравнения (2). Для различных комбинаций параметров a и f были выполнены контрольные эксперименты по экстраполяции заданного в начальный момент начального возмущения функции тока. Затем расчеты были повторены, но с добавлением в правую часть системы уравнений источника завихренности. В соответствии с [Хелд, 1988] источник завихренности был задан в виде

На рис. 2 приведены в нормализованном виде периоды колебаний наиболее неустойчивых мод (единица измерения периодов колебаний – 1 оборот Солнца). Отрицательные значения соответствуют движению нормальных мод в направлении вращения, положительные – движению в противоположном направлении. Областям перемены знака соответствуют стационарные колебания. Согласно результатам расчетов, в среднем периоды колебаний меньше в области устойчивого дифференциального

2u Ω sin ϕ ∂htop R=-            , ha cos ϕ ∂λ

где u – средняя скорость потока, набегающего на препятствие, h – средняя толщина слоя жидкости, h top – конфигурация верхней границы слоя жидкости.

Шаг по времени был принят равным 0.005 оборота Солнца, общее время счета составило примерно четырнадцать оборотов Солнца. Рассчитывалось изменение со временем интенсивности сферических

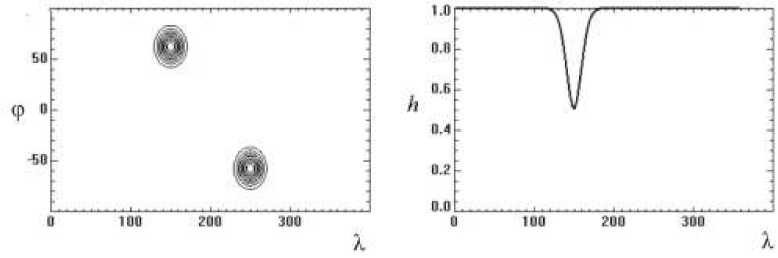
Рис. 3 . Горизонтальная (слева) и вертикальная (справа) структура локальных неоднородностей верхней границы слоя жидкости.

гармоник в разложении возмущения функции тока

EY=(VyR )2 +(VYI )2, а также их суммы. Неоднородности верхней границы слоя жидкости были заданы в виде суммы двух экспонент в северном и южном полушариях Солнца:

hT (X, 0) =△ h[exp(-(X - X, )2 [d - (0 - 0, )2 /d)) ++ exp (-(X-X2)2 /d-(0-02)2 /d,)].

△ hh = 0.5.

На рис. 3 слева приведена горизонтальная структура верхней границы слоя жидкости с заданными неоднородностями толщины слоя, на рис. 3 справа – вертикальное сечение слоя жидкости вдоль параллели, проходящей через центр неоднородности северного полушария Солнца. Скорость набегающего потока u определялась разностью скоростей дифференциального вращения на широте заданных неоднородностей толщины слоя (60°) и на широте 30°.

На рис. 4 приведен пример эволюции со временем начального возмущения функции тока для параметров дифференциального вращения a =0.2, f =0.2 и при заданных неоднородностях толщины слоя. Интервал между соседними распределениями – 2.1 оборота Солнца. Контрольный эксперимент показал, что дифференциальное вращение без неоднородностей устойчиво. Включение источников завихренности приводит к росту интенсивности возмущений. Неустойчивость проявляется в усилении возмущений вблизи источника завихренности в северном полушарии и в появлении возмущений в широтной полосе источника завихренности в южном полушарии. Положение источников завихренности выделено кружками.

Особенно хорошо рост неустойчивости течения виден на графиках рис. 5, показывающих изменение со временем интенсивности сферических гармоник. На рис. 5 слева нанесены графики контрольного эксперимента, на рис. 5 справа – графики численного эксперимента с источниками завихренности. Каждый график соответствует изменению интенсивности сферических гармоник с фиксированным меридиональным числом n . Особенно интересно поведение дипольной компоненты n =1. Кроме роста со временем амплитуды этой компоненты выделяются колебания с характерным временным масштабом

8–10 оборотов Солнца, причем период колебаний зависит от условий эксперимента.

Аналогичные расчеты изменений интенсивности возмущений были выполнены и для других наборов параметров a и f . Для сопоставления с характеристиками нормальных мод осесимметричного дифференциального вращения для каждого a и f оценивались темпы роста энергии возмущений по формуле

"=ln flE)/ • где lEq , l ET - суммы «энергии» сферических гармоник в начальный момент времени и в конце эксперимента в момент времени T. На рис. 6 приведены полученные оценки темпов роста возмущений. Прямоугольником выделена область параметров дифференциального вращения, соответствующих условиям на Солнце. Видно, что дифференциальное вращение стало неустойчивым практически при всех значениях параметров a и f. При заданных неоднородностях толщины слоя и скорости набегающего потока характерное время роста интенсивности возмущений в области солнечных параметров составляет несколько десятков оборотов Солнца. Задание другой структуры источников завихренности и горизонтального поля скорости может существенно изменить полученный результат. Особенно вероятно появление неоднородностей в высоких широтах, для которых характерны большие вертикальные градиенты угловой скорости дифференциального вращения.

Результаты

Численные эксперименты с квазигеострофиче-ской баротропной моделью показали, что неоднородности толщины слоя тахоклина дестабилизируют дифференциальное вращение. Дифференциальное вращение становится неустойчивым во всей области параметров, характерных для дифференциального вращения Солнца. Темпы роста неустойчивостей зависят от горизонтальной и вертикальной структуры неоднородностей толщины слоя, а также от скорости набегающего потока. Для локальных возмущений толщины слоя, использованных в расчетах, характерный временной масштаб роста возмущений составляет несколько десятков оборотов Солнца и примерно в два раза меньше времени роста неустойчивых нормальных мод. Как показывают предва-

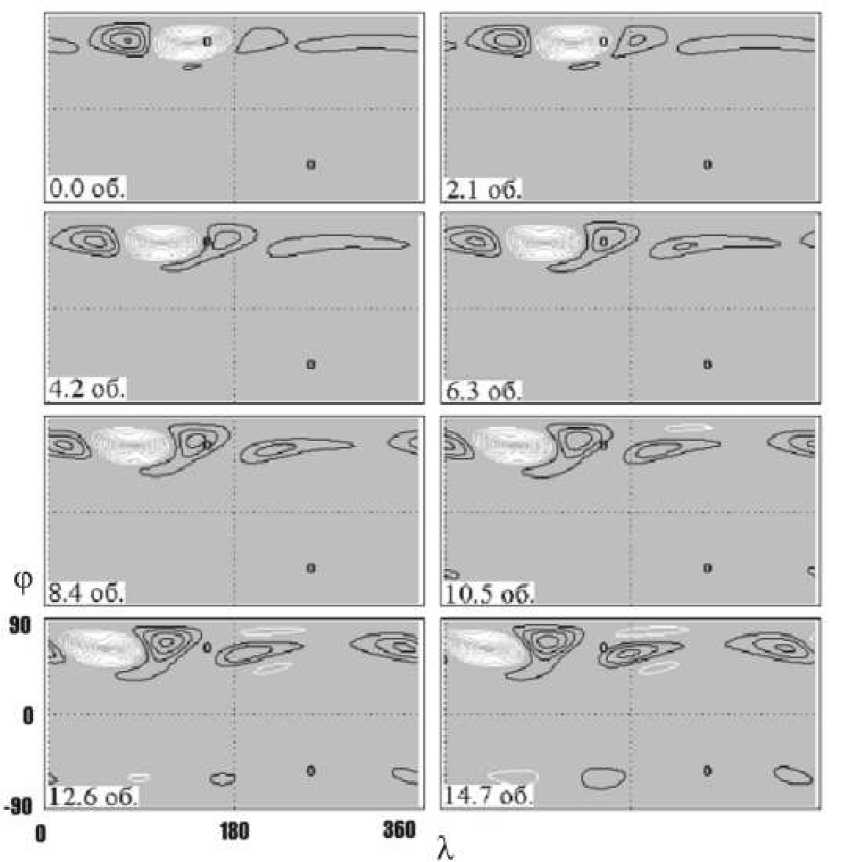
Рис. 4 . Эволюция начального возмущения функции тока. Нанесены изолинии функции тока, нормированные на максимальное значение для данного момента времени.

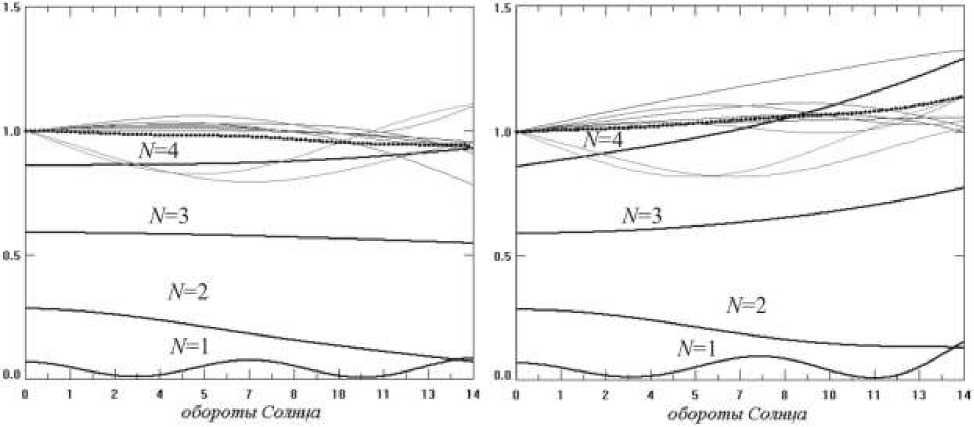
Рис. 5. Изменения со временем интенсивности сферических гармоник с фиксированным меридиональным числом n для контрольного эксперимента (слева) и для эксперимента с источниками завихренности (справа). Значения интенсивности нормированы на максимальное значение в начальный момент времени. Толстой пунктирной линией показано изменение суммарной интенсивности сферических гармоник в относительных единицах.

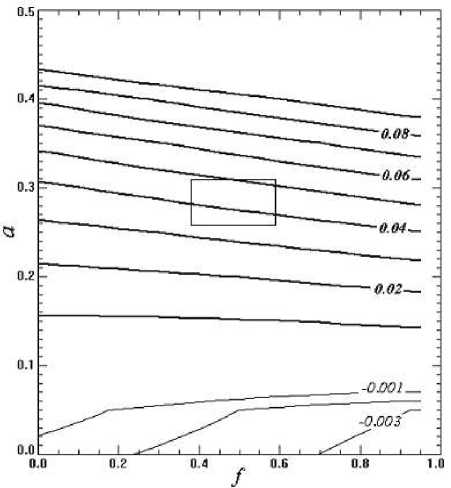
Рис. 6 . Зависимости нормализованных скоростей роста интенсивности возмущений от параметров a и f , характеризующих дифференциальное вращение.

рительные оценки, если неоднородности толщины слоя равномерно заполняют верхнюю поверхность тахоклина, эффективность раскачки неустойчивостей значительно возрастает и может составить менее десяти оборотов Солнца.

К сожалению, данные глобальной гелиосейсмологии не дают информации о реальной структуре тахоклина, поэтому приведенные выше результаты численных экспериментов следует считать лишь предварительной оценкой возможности подобного механизма развития неустойчивостей.

Хелд А. Теория стационарных и квазистационарных вихрей во внетропической тропосфере // Крупномасштабные динамические процессы в атмосфере. М.: Мир, 1988. С. 143–189.

Cally P.S. Three-dimensional magneto-shear instabilities in the solar tachocline // Mon. Not. R. Astron. Soc. 2003. V. 339, Iss. 4. P. 957–972.

Dikpati M., Gilman P.A. A shallow-water theory for the sun’s active longitudes // Astrophys. J. 2005. V. 635, Iss. 2. P. L193–L196.

Gilman P.A. Stability of baroclinic flows in a zonal magnetic field. Part 1–3 // J. Atmos. Sci. 1967. V. 24, N 2. P.101–118. P. 119–143.

Gilman P.A., Fox P.A. Joint instability of latitudinal differential rotation and toroidal magnetic fields below the solar convection zone // Astrophys. J. 1997. V. 484, N 1. P. 439–454.

Gilman P.A., Dikpati M., Miesch M.S. Global MHD instabilities in a three-dimensional thin-shel model of solar tachocline // Astrophys. J. Suppl. Ser. 2007. V. 170. P. 203– 227.

Lou Yu-Qing. Rossby-type wave-induced periodicities in flare activities and sunspot areas or groups during solar maxima // Astrophys. J. 2000. V. 540, N 2. P. 1102–1108.

Tikhomolov E.M. Large-scale vortical flows and penetrative convection in the Sun // Nucl. Phys. A. 2005. V. 758, N 1–4. P. 709–712.

Tikhomolov E.M., Mordvinov V.I. The peculiar behavior of the large-scale components of the solar magnetic field as a result of Rossby vortex excitation beneath the convection zone // Astrophys. J. 1996. V. 472, N 1. Part 1. P. 389–397.

Zagarashvili T.V., Carbonell M., Oliver R., Ballester J.L. Magnetic Rossby waves in the solar tachocline and Rieger-type periodicities // Astrophys. J. 2010. V. 709, N 2. P. 749–758.

Институт солнечно-земной физики СО РАН, Иркутск, Россия