Гидродинамические неустойчивости в тахоклине, обусловленные вариациями толщины слоя и неоднородностями среднего потока

Многие из наблюдаемых образований магнитного поля на поверхности Солнца до сих пор не имеют однозначного объяснения и не соответствуют результатам численного моделирования, основанного на воспроизведении конвекции и турбулентности. В первую очередь это относится к крупномасштабным структурам магнитного поля, которые можно условно разделить на два основных типа: 1) структуры, тесно связанные с сильными магнитными полями, – активные долготы, ПДА и т. п.; 2) структуры фонового поля. Особый интерес и своего рода загадку представляют структуры второго типа, для которых пока не существует удовлетворительного объяснения. Время жизни этих структур сопоставимо с продолжительностью солнечного цикла или даже превосходит ее [Бумба, 1979; Бумба, Макаров, 1989; Bumba, Howard, 1965].

Свойствами, необходимыми для возникновения и большого времени существования крупномасштабных МГД-структур, обладает только двумерная турбулентность, при которой энергия переносится в область малых волновых чисел. Областью, где может возникать двумерная турбулентность, является тахоклин – тонкий переходный слой между солнечными оболочками с различными режимами вращения: дифференциально вращающейся конвективной зоной и радиативной оболочкой, в которой вращение практически твердотельно. Необходимым условием возникновения двумерной турбулентности в тахоклине является либо наличие достаточно сильного тороидального поля, либо внешнее воздействие, так как при отсутствии внешних воздействий и собственного магнитного поля тахоклин должен быть устойчив. Большое количество работ [Gilman, Fox, 1997; Dikpati, Gilman, 2001; Cally et al., 2003; Gilman et al., 2007] посвящено первому варианту генерации неустойчивостей – совместному действию дифференциального вращения и сильного тороидального поля. В зависимости от структуры начального тороидального поля в таких моделях развиваются неустойчивости двух типов:

• 1)    тороидальные магнитные поля, имеющие плавный профиль широтной зависимости, приводят к развитию грейферной неустойчивости (clamshell instability);

• 2)    узкие тороидальные полосы в процессе развития наклоняются относительно экватора, образуя так называемые наклонные неустойчивости (tipping instability).

С точки зрения приложения к наблюдаемым особенностям магнитных полей на Солнце наибольший интерес представляют tipping-неустойчивости. Ряд исследований [Dikpati, Gilman, 2005; Norton, Gilman, 2005] посвящен поиску проявлений tipping-неустойчивости в наблюдательных данных. Объектом сопоставления в данном случае являются только структуры, связанные с сильными магнитными полями. В отсутствие сильных тороидальных магнитных полей, т. е. в минимуме цикла и в широтных зонах вне зоны солнечных пятен, tipping-неустойчивость не должна возникать. Таким образом, результаты моделирования неустойчивостей в тахоклине, основанного на совместном действии дифференциального вращения и сильного тороидального поля, не могут претендовать на объяснение крупномасштабных и сверхдолгоживущих структур фонового поля.

Как уже говорилось выше, еще одним условием возникновения двумерной турбулентности, приводящей к возникновению долгоживущих МГД-структур, может быть внешнее воздействие на тахоклин – например, реликтовое магнитное поле, которое вследствие медленной диффузии может проникать в тахоклин и немного искажать либо его толщину, либо структуру среднего потока. Крупномасштабные гидродинамические структуры, проявлением которых в фотосфере могут быть обширные области фонового магнитного поля или комплексы активности, могут также формироваться в верхней части тахоклина, названной активным переходным слоем (АПС) в работе [Tikhomolov, Mordvinov, 1996]. Образование в слое проникающей конвекции долгоживущих гидродинамических структур способствует более эффективному перемешиванию плазмы в тахоклине, чем может объясняться низкое содержание лития в солнечной атмосфере [Tikhomolov, 2005]. В работе [Zagarashvili et al., 2010] показано, что в тахоклине могут развиваться колебания типа волн Россби– Альфвена, свойства которых могут быть связаны с колебаниями солнечной активности в фотосфере и короне в диапазоне периодов 155–160 сут.

Настоящая работа является продолжением ранее начатых нами исследований [Мордвинов и др., 2012], цель которых – показать, что включение в рассмотрение внешнего воздействия, а именно долготных неоднородностей в среднем поле скорости, действительно существенно меняет устойчивость среднего потока и характер нормальных мод. В отличие от авторов работ [Dikpati, Gilman, 2001; Cally et al., 2003; Miesch et al., 2007], мы отказались от приближения зональной симметрии и допустили возможность существования в структуре среднего течения долготных неоднородностей, время жизни которых много больше времени развития неустойчивостей. В баротропном приближении эти неоднородности можно задать двумя способами – изменяя структуру среднего течения либо вводя в рассмотрение неоднородности толщины слоя.

Модель

Для оценки неустойчивостей в тахоклине была использована баротропная дивергентная квазигео-строфическая гидродинамическая модель. В приближении зональной симметрии среднего потока такая модель применяется для изучения течений в подповерхностных слоях Солнца, начиная с исследований Гилмана в 60-х гг. прошлого века [Gilman, 1967]. В работе [Dikpati, Gilman, 2001] подробно рассматриваются свойства этой модели применительно к анализу крупномасштабных течений на Солнце.

Основой модели является уравнение квазигео-строфического потенциального вихря

(1 ⁺ v g ^V h ] П = ^ , ⁽¹⁾ где n = l + A v - R_d ~ V + h /h — квазигеострофический потенциальный вихрь, v g = k x Vv , V = ( g/l ) h — функция тока, h ( X , 9 ) - свободная верхняя граница слоя жидкости, h T ( X , 9 ) - фиксированная нижняя граница слоя жидкости, h ₀ – средняя толщина однородного слоя жидкости, l =2 Оц - параметр Кориолиса, О -угловая скорость вращения Солнца, R ^ ^gh jl -радиус деформации Россби-Обухова, X - долгота, ц =cos 9 , 9 - полярный угол, rot z F mp - вертикальная компонента вихря силы трения.

Нетривиальную задачу в квазигеострофическом приближении представляет параметризация вязкости. Хотя обычная вязкость ~vA и в принципе обеспечивает диссипацию энстрофии, для расширения инерционного интервала энстрофии обычно используют диссипацию на более коротких длинах волн вида

F =(-1) N ⁺¹ K A N ( Av ), N > 1 (гипервязкость) [Данилов, Гурарий, 2000]. При N =1 формула для F соответствует обычной турбулентной вязкости, а коэффициент K равен коэффициенту эффективной турбулентной кинематической вязкости v . Применительно к атмосфере Земли параметризацию с N =2 использовали для предотвращения сингулярности на критических уровнях [Grose, Hoskins, 1979]. К сожалению, не ясно, какие значения степени N и коэффициента K следует использовать для параметризации солнечного тахоклина. Мы использовали в расчетах параметризации N =1, 2, 3, а коэффициент K подбирали таким образом, чтобы гипервязкость равнялась обычной вязкости v =10¹² см²с^-1 для выбранных гармоник в разложении функции тока. В дальнейшем мы будем обозначать этот коэффициент как K_i j , где i – степень дифференциального оператора N , а j – степень выбранной сферической гармоники.

Кроме энстрофии в двумерной задаче необходимо обеспечить также подавление каскада энергии в направлении малых волновых чисел. Это достигается включением искусственной длинноволновой диссипации, которая отсутствует в строго двумерном случае [Данилов, Гурарий, 2000]. Чаще всего для этого используют рэлеевское трение на малых волновых числах F = r ( Av ). В численных расчетах роль рэлеевского трения сводится к сдвигу вещественных частей частот колебаний на одно и то же число r [Дымников, Скиба, 1986]. Пространственная структура нормальных мод при этом не меняется. К сожалению, увеличение количества свободных параметров в задаче не позволяет надеяться на воспроизведение реальных процессов в тахоклине и ограничивает выводы лишь констатацией качественных эффектов, хотя и это, на наш взгляд, представляет интерес.

В качестве угловой скорости вращения системы отсчета О будем принимать угловую скорость вращения аномалий толщины слоя жидкости, а при их отсутствии – скорость вращения Солнца на экваторе. Подставляя в (1) выражение для геострофической скорости, получаем уравнение для функции тока:

d( L V ) = ± х dt R2

dv d ( L V + lh_T,h» ) dv d ( L V + lh_T/h )

_ dц dX ex dц

- (2)

2О dv R ² 5X

- r A v - K A ² ( A v ) ,

где L v ^ ( a - R - 2 ) v , R - радиус Солнца.

Линеаризуя (2) относительно среднего распределения функции тока, получаем уравнение для возмущений функции тока:

dLV’ _ _1

R ²

" d V d ( L V + lhr/h 0 ) _ d v ' d ( L V + lhT/h 0 )

X 5ц      dX        dX      5ц      + dv dLv' дц dX

d v d L v ' d X д ц

2 О d v '

R ² d X

^— r A v '^— K A ² ( ^A v ' ) = 12^ [ J ( G , v ' ) + J ( ^L v', V ) ] R

—

— 2^_ r Av' — к a 2 (Av') ;                 (3)

R^г a x                ^{V 7}                        ( )

j(f _g) = ^f — f ^d g •

^(/,^g)   a x д ц   д ц ax’

G = L v + lh_T[h_Q .

Если представить функцию тока среднего течения в виде суммы осесимметричной составляющей (дифференциальное вращение) и аномалий

v ( ц, x ) = v s ( ц ) + v as ( ц, x ) , то уравнение (3)

можно записать в форме

al v'     1  r-.

• ⁼ R^{7 [} F ^{1 +} F ^{2 +} F ^{3 ] —}

2Q dv'       ,

• — —--- — r A v — K A ( A v ) .

r 2

Дифференциальные операторы F 1 , F 2 , F 3 имеют различную степень и определяют взаимодействие возмущений у' с осесимметричной компонентой среднего потока, аномалиями среднего потока и аномалиями толщины слоя:

F i = J ( L v s , v ' ) + J ( L v', v s ) ,

F 2 = J ^{( L v} as ,v '^{) +} J ^{( L} V,V as ) ,              ⁽⁵⁾

F = j ( ih_T/F . v ' ) .

Представим возмущение функции тока в виде нормальной моды [Дымников, Филатов, 1988]:

v ' ( ^x , ц, t ) = e ° t 2 v y^Yy ( ц^,x ) ,              ⁽⁶⁾

γ

где a - комплексная частота, y =( m, n )=( m _Y , n _Y ) - волновой вектор, m – зональное волновое число, n – степень сферической функции Y ^ ( X , р ).

Выберем в качестве масштаба длины радиус Солнца, а в качестве масштаба времени - Q ^-1. Введем обозначения

1₂ r = — { r + Kn

Q 1

( n + 1 )2 [a ⁴ } . k_n = n ( n +1)+ F 2 ,

где F = R / R D - число Фруда. Учитывая свойство сферических функций AY _y =- n ( n +1) Y ^ / R 2 , получаем после подстановки (6) в уравнение (3) и интегрирования по сферической поверхности уравнения для коэффициентов разложения функции тока V y :

k _n ' o'v_Y ' = v_Y ' ( n ' ( n’ + 1 ) r 1 + i 2 m' ) +

+ 2 W y J Y^J ( Y Y , G n ) ds ,                 (7)

^Q Y     s

где

G' _n =A v + k _n v + lh _T/ h ₀ , o'=o/Q ,

или в матричном виде

A yy ' v Y ⁺ °Vy ' = 0,

где

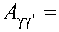
8„'

1 k ^ Q

- 2 v , J Y ,* ^J ( Y , . G n ) d^S

. Y        S

.² m ' .

i --+ r

L k n ¹

n ' ( n' + 1 )

kn'

Анализ неустойчивости течения сводится к нахождению собственных чисел и собственных векторов матрицы A . Собственные числа определяют частоты (комплексные) колебаний нормальных мод, а собственные векторы – пространственную структуру нормальных мод. И те, и другие зависят от возмущений среднего потока и возмущений толщины слоя.

Если использовать в качестве искомой величины не функцию тока, а завихренность, матричное уравнение для коэффициентов разложения возмущений завихренности по сферическим функциям п ' примет вид

A YY ' H , ⁺ °'Л , = 0,

A Y ,= ² К v , J Y ,* ^J ( Y , . G n/ k n ) d^S - —

^Q I Y     S

Уравнения (8) и (9) эквивалентны, однако при численном решении дают несколько различные результаты. Сопоставление результатов позволяет контролировать точность численных расчетов.

В работе [Gilman, Dikpati, 2007] приближение «мелкой воды» использовалось для исследования неустойчивости в «радиативной» части тахоклина и в слое проникающей конвекции. Возможность подобного дифференцированного подхода обусловлена зависимостью числа Фруда от характерного вертикального масштаба плотности, различного в каждом из слоев. В использованной нами модели квадрат числа Фруда является аддитивной добавкой в выражении для коэффициента k n . Оценим вклад этой составляющей. Введем обозначение k = h ₀ / R . Тогда F ² « 4 R Q ² ( sin 45° ) 2 ^gk = 2 R Q ²/ gk = 4.36 • 10 ^—6/ k . Отсюда следует, что при любых h 0 , аппроксимирующих толщину тахоклина, вклад аддитивного члена мал и коэффициент k_n ^ n ( n +1).

Как мы уже отмечали, одной из проблем моделирования квазидвумерных течений является параметризация вязкости, от которой зависит не только величина, но и сходимость численного решения. В работе [Дымников, Скиба, 1986] асимптотическая сходимость численного решения доказана для ненулевых значений коэффициентов рэлеевского трения и гипервязкости N =2 и подтверждена численными расчетами на конкретном примере. Мы провели аналогичные расчеты для условий дифференциального вращения Солнца и различных параметризаций вязкости.

Для решения матричного уравнения применялась стандартная процедура LA-EIGENPROBLEM языка

программирования IDL. Интеграл по переменной X вычислялся с использованием квадратурной формулы прямоугольников, а интеграл по переменной ц с использованием квадратуры Гаусса [Дымников, Скиба, 1986]:

1 _K

J f (ц) d ц®^ Ckf (цк ) ,

• - 1                  к = 1

где   ц к - корни полиномов Лежандра P k ( ц ).

C k

2 ( 1 — Н к )2

[KPK-1 (Нк )]2 , k=1, 2, …, K.

Число узлов по переменной X составляло 144, по переменной ц - 64.

Результаты

Осесимметричное течение . F 2 = F 3 =0

Рассмотрим сначала устойчивость осесимметричной составляющей среднего потока жидкости. Зададим профиль дифференциального вращения в форме, предложенной в работе [Kitchatinov, Rüdiger, 2009]:

П = П₀( 1 - a ( ( 1 - f ) cos ² 0 + f cos ⁴ 0 )) , (10)

где Q ₀ — угловая скорость дифференциального вращения Солнца на экваторе, коэффициенты a и f определяют профиль дифференциального вращения.

На рис. 1 приведены графики зависимостей инкрементов роста наиболее неустойчивой нормальной моды от числа гармоник в разложении функции тока. Использовались различные параметризации вязкости, параметры дифференциального вращения были приняты равными a = f =0.5. Согласно [Kitchatinov, Rüdiger, 2009], при этих значениях a и f осесимметричное течение жидкости является слабо неустойчивым. Номерами 1, 2, 3 обозначены зависимости, соответствующие вязкости N =1 с коэффициентами v ₀ =0, v ₁ =10¹², v ₂ =10¹⁴ см²с^-1, номерами 4, 5 - зависимости, построенные для гипервязкости N =2 с коэффициентами турбулентной вязкости K ₂₁ , K ₂₄ . Время рэлеевского затухания во всех случаях было принято равным 100 оборотам Солнца ( r 100 ).

Можно видеть, что за исключением обычной турбулентной вязкости N =1 с коэффициентом v ₂ =10¹³ см²с^-1 остальные параметризации дают близ-

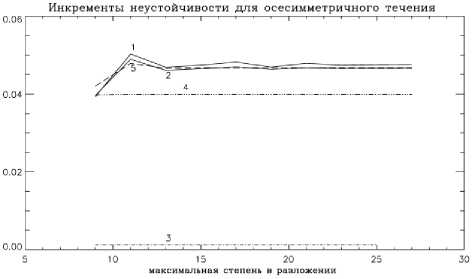
Рис. 1. Зависимости инкрементов роста наиболее неустойчивой нормальной моды от числа гармоник в разложении функции тока для дифференциального вращения a = f =0.5. Кривые 1, 2, 3 соответствуют вязкости N =1 с коэффициентами v 0 =0, v ₁ = 10¹², v ₂=10¹⁴ см²с^{- 1} , кривые 4, 5 – гипервязкости N =2 с коэффициентами K ₂₁ и K ₂₄.

кие значения инкрементов роста неустойчивостей в диапазоне характерных временных масштабов Q ₀ /Re( a )~20-25 оборотов Солнца. При вязкости v ₂ =10¹³ см²с^-1, соответствующей зоне конвекции, время роста возмущений составляет 850 оборотов, т. е. осесимметричное течение является фактически устойчивым. Лучше всего условиям тахоклина ( v ₂ =10¹² см2с^-11) соответствует гипервязкость, нормированная на гармонику n =1 в разложении возмущений (коэффициент K 21 ). Из результатов расчетов следует также, что с возрастанием вязкости несколько улучшается сходимость численного решения. Практически совпадают результаты расчетов, выполненных по формулам (8) и (9). В абсолютных единицах разности инкрементов, рассчитанные по этим формулам для гипервязкости K ₂₁ , различаются не более чем на 10^–4. Таким образом, для осесимметричного течения проблема сходимости решения не возникает. Даже при нулевой турбулентной вязкости вариации собственных значений матрицы A в зависимости от количества гармоник в разложении оказываются небольшими. Характерные временные масштабы развития неустойчивостей варьируют в пределах от 20 до 25 оборотов Солнца.

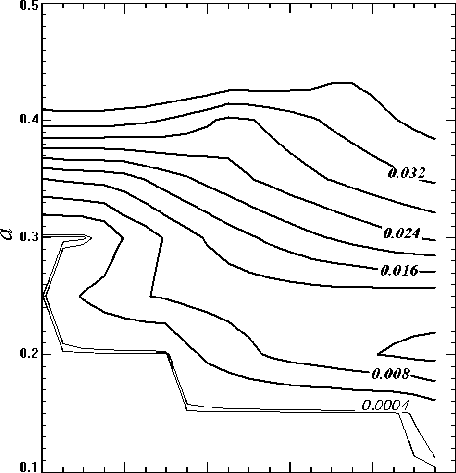
Чтобы проиллюстрировать связь между неустойчивостями и характеристиками дифференциального вращения, на рис. 2, 3 представлены зависимости частот собственных колебаний от параметров дифференциального вращения a и f для нормальных мод, имеющих максимальные инкременты роста. Расчеты выполнены для нулевой турбулентной вязкости и времени рэлеевского затухания 1000 оборотов Солнца, максимальная степень в разложении возмущений функции тока была принята равной 11. Согласно предыдущим расчетам, этим условиям соответствуют наибольшие инкременты роста неустойчивостей. На рис. 2 изображены распределения нормализованных скоростей роста наиболее неустойчивых мод Q ₀ /Re( a ). В левой нижней части рис. 2 значения инкрементов меньше нуля, эта часть рисунка соответствует устойчивому дифференциальному вращению. В правой верхней части рисунка инкременты нормальных мод положительные и увеличиваются с ростом коэффициентов a и f . Сравнение с результатами, приведенными в работе [Kitchatinov, Rüdiger, 2009], показало, что по порядку величины полученные инкременты близки к скоростям роста нормальных мод с зональным волновым числом m =1, рассчитанным с учетом вертикальной структуры возмущений в работе [Kitchat-inov, Rüdiger, 2009]. Однако горизонтальная структура наиболее неустойчивых мод в наших расчетах оказалась более сложной, с преобладанием мелкомасштабной составляющей.

На рис. 3 приведены в нормализованной форме периоды колебаний наиболее неустойчивых мод Q ₀ /Im( a ). Положительные значения соответствуют движению нормальных мод в направлении вращения, отрицательные – движению в противоположном направлении. Областям перемены знака соответствуют стационарные колебания. Можно видеть, что в области слабой неустойчивости периоды колебаний сильнее зависят от параметра f , чем от параметра a .

0.0          0.2          0.4          0.0          0.8         1.0

Рис. 2. Зависимости нормализованных скоростей роста наиболее неустойчивых мод от коэффициентов a и f , характеризующих дифференциальное вращение.

0.5 —'—।--'—|--1—'--'—|--'—।--1—|--1—'--'—|--'—।--г

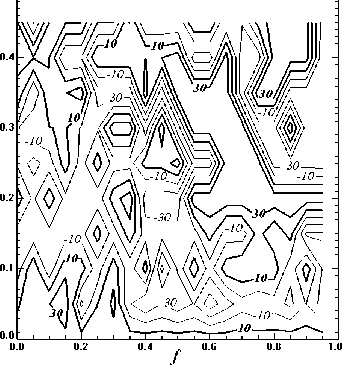
Рис. 3. Периоды колебаний наиболее неустойчивых мод (единица измерения – 1 оборот Солнца). Толстые линии – движение нормальных мод в направлении вращения, тонкие – движение в противоположном направлении.

В целом результаты расчетов показали, что осесимметричное дифференциальное течение жидкости достаточно стабильно в широком диапазоне параметров, поэтому гидродинамическими неустойчивостями зонально-симметричного потока сложно объяснить все многообразие наблюдаемых на Солнце быстро протекающих явлений. Инкременты роста нормальных мод оказываются для этого слишком малыми, а периоды колебаний в большинстве случаев слишком большими. Рассмотрим теперь, какое влияние на неустойчивости дифференциального вращения оказывают долготные неоднородности течения, обусловленные аномалиями среднего потока и аномалиями толщины слоя. Разделять эти два фактора, вообще говоря, не вполне корректно, однако самосогласованное решение можно получить лишь при трехмерной постановке.

Влияние на устойчивость тахоклина возмущений среднего потока. F 1 * 0, F 2 * 0, F 3 =0

Примем G ‘ = A V + k_n V. Если аппроксимировать аномалии среднего потока суммой сферических гармоник, то функция тока среднего течения примет вид

• — n2rx (л -т\1 ^Ц I I ^Ц

V = R ^оa (1 - f )1    1 + f I

V       V 3 v V 5

+ Е gY YY ( Х,Ц ) .

γ

+

^V            (11)

Вообще говоря, ψ должна удовлетворять стационарному уравнению

-J ^{J (} V, G ) = q

—

2 Q d V

R ² ЭХ

— r A v — KA² ( A v ) , G = L V,

где функция q описывает суммарное воздействие нестационарных бароклинных возмущений на баротропную составляющую потока. В общем случае при достаточно широком классе q и h T решение уравнения (12) представляет собой сложную задачу, однако при любом h T можно подобрать q таким образом, чтобы стационарное решение существовало [Дымников, Филатов, 1988]. Так как представления о структуре возмущений тахоклина отсутствуют, мы ограничились заданием возмущений в виде одной из сферических гармоник. Амплитуда g сферической гармоники подбиралась из условия слабого влияния возмущений на среднее течение. Условием слабого влияния было отсутствие в среднем потоке замкнутых линий функции тока. Численные оценки показали, что в этом случае величина g должна быть 0.01–0.02 и меньше по отношению к амплитуде функции тока дифференциального вращения.

К сожалению, для задания возмущений функции тока ψ мы можем опираться лишь на косвенные данные, так как локальная гелиосейсмология позволяет анализировать структуру течений только в тонком подповерхностном слое Солнца [Miesch, 2005]. Можно предположить, что структуру среднего течения отражают распределения крупномасштабных полей и/или комплексов активности. И те и другие имеют большое время жизни, поэтому они могут влиять на структуру среднего течения в тахоклине, а возможно, и в радиативной зоне. Так как нас пока интересует лишь степень влияния возмущений на неустойчивости среднего течения, будем задавать аномалии среднего течения в виде отдельных сферических гармоник.

Представим возмущение среднего течения в виде гармоники gP65 (ц) cos5X. На рис. 4, а приведена пространственная структура этой гармоники. На наш взгляд, структура этой сферической функции реалистично отражает структуру крупномасштабных магнитных полей вблизи максимума солнечного цикла. На рис. 4, б показано распределение суммы функций тока дифференциального вращения с параметрами a=0.5 и f=0.5 и заданного возмущения с амплитудой g=0.01. Если оценивать искажения среднего потока визуально, то они весьма невелики и незначительно изменяют структуру осесимметричного дифференциального вращения. Это хорошо видно и на рис. 4, в, на котором сплошной линией изображен неискаженный профиль дифференциального вращения, а штриховой линией - профиль дифференциального вращения с учетом заданного возмущения.

На рис. 5 приведены графики инкрементов роста наиболее неустойчивой нормальной моды в зависимости от числа гармоник n в разложении функции тока при различных амплитудах возмущения среднего потока и параметризациях вязкости. Характеристики дифференциального вращения принимались равными a = f =0.5. На рис. 5, а представлены зависимости инкрементов от величины n при различных амплитудах возмущения g для гипервязкости N =2, характеризуемой коэффициентами r ₁₀₀ и K ₂₁ . На рис. 5, б приведены зависимости инкрементов для различных коэффициентов K гипервязкости N =2 и для вязкости N =1 с различными коэффициентами v . Кривые 1, 2, 3, 4 соответствуют коэффициентам K ₂₁ , K ₂₂ , K ₂₃ , K ₂₄ , кривые 5, 6, 7 - турбулентной вязкости с коэффициентами кинематической вязкости v =10¹², 10¹³, 10¹⁴ см²с^-1. График инкрементов при v =10¹² см²с^-1 практически совпадает с графиком инкрементов при нулевой турбулентной гармоники вязкости, т. е. обычно принимаемая для тахоклина турбулентная вязкость не влияет на развитие баротропной неустойчивости. На рис. 5, в приведены зависи-

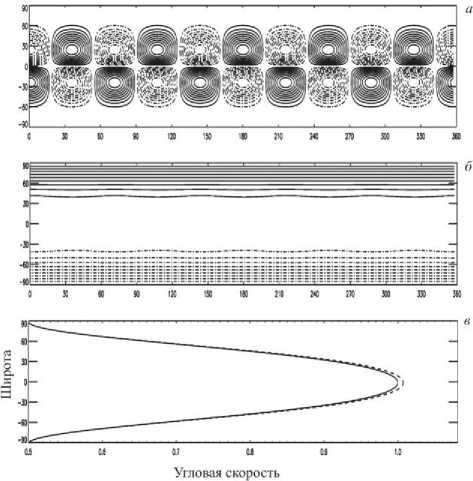
Рис. 4. Пространственная структура гармоники P 5 ( р ) cos5X ( а ); пространственная структура функции тока осесимметричного дифференциального вращения (6) и сферической функции gP ⁵ ( р ) cos5X ( б ); изолинии построены в относительных единицах. Угловые скорости дифференциального вращения П / П ₀ (штриховая линия) и суммы осесимметричного дифференциального вращения и зональной составляющей геострофической скорости gP 5 ( р ) cos5X (сплошная линия) ( в ).

мости инкрементов от числа гармоник n для гипервязкости N =3 и коэффициентов K , нормированных на турбулентную вязкость для сферических гармоник 1, 2, 3 и 4 (коэффициенты K ₃₁ , K ₃₂ , K ₃₃ , K ₃₄ ). Амплитуда возмущения среднего потока принималась равной g =0. 01 . На этом же рисунке показаны графики инкрементов для возмущений с амплитудами g =0.02 , 0.03 при коэффициенте гипервязкости K ₃₃ .

Первое, что следует отметить, это существенно возросший уровень неустойчивости по сравнению с осесимметричным средним потоком. Даже при относительно небольших амплитудах возмущения среднего потока g =0.005-0.01 инкременты увеличились почти на порядок. Вторая особенность - сильная зависимость инкрементов от количества гармоник в разложении возмущений функции тока, причем высота и положение максимума инкрементов зависят от амплитуды возмущения среднего потока g и от параметризации вязкости. При увеличении амплитуды максимум инкрементов на рис. 4, а растет и смещается в направлении увеличения n . Еще более быстрыми темпами растут инкременты, если гипервязкость нормировать не на дипольную гармонику, а на гармоники более высокой степени или использовать обычную турбулентную вязкость с коэффициентами v , соответствующими основанию конвективной зоны (рис. 4, б ). Только при очень большой турбулентной вязкости v~ 10¹⁴ см²с^-1 удается подавить рост инкрементов в зависимости от числа гармоник в разложении, течение в этом случае становится устойчивым. Более приемлемым является использование гипервязкости N =3 . При небольшой амплитуде возмущения инкременты неустойчивости сходятся, они близки к инкрементам для гипервязкости N =2 и не очень сильно зависят от нормировки коэффициента K . С увеличением g различия в поведении инкрементов возрастают. При N =3 максимум инкрементов в области n « 20 эффективно подавляется и результаты расчетов сходятся к значениям инкрементов, пропорционально растущим с увеличением амплитуды возмущения g .

Зависимость результатов расчетов от параметризации вязкости вносит неопределенность в решение задачи. Достоверно можно лишь утверждать, что долготные неоднородности в структуре среднего потока существенным образом усиливают баротропную неустойчивость среднего потока, однако более или менее точно оценить скорость роста неустойчивости практически невозможно. Еще более сложной является проблема пространственной структуры неустойчивости. Во-первых, инкременты роста наиболее неустойчивых мод отличаются не очень сильно, чего нельзя сказать о пространственной структуре этих мод. Во-вторых, пространственная структура наиболее неустойчивой моды зависит от количества сферических гармоник в разложении функции тока. При сильной вязкости N ≥2 с увеличением n пространственная структура наиболее неустойчивой моды становится асимптотически устойчивой с преобладанием в разложении составляющих из подпространства n =8, однако не вполне понятно, насколько асимптотика отражает действительность. Кроме того, асимптотика зависит от структуры среднего потока.

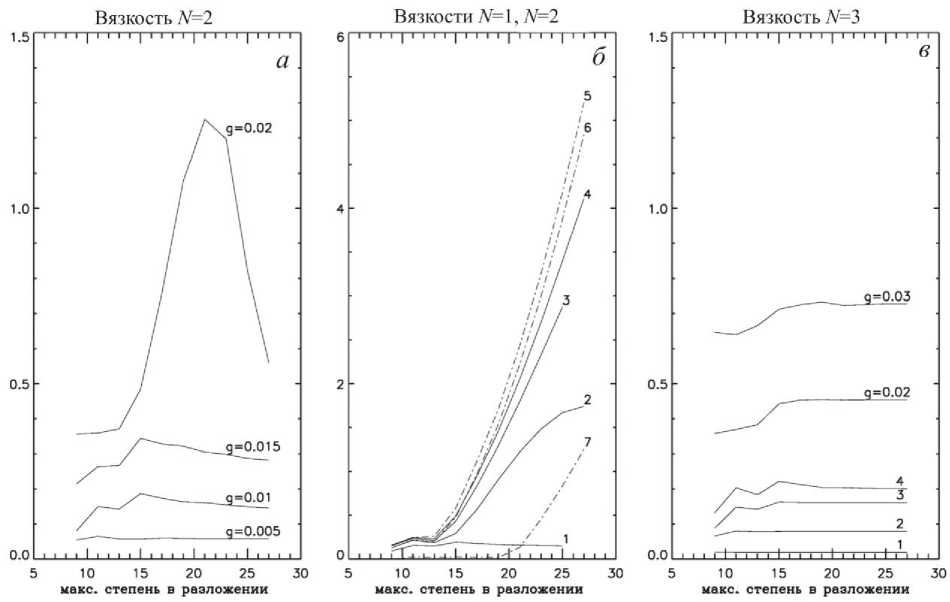
Рис. 5. Зависимость инкрементов роста наиболее неустойчивой нормальной моды от числа гармоник n в разложении при различных амплитудах g и вязкости, определяемой коэффициентами r ₁₀₀ и K ₂₁ (рис. 5, а ), при различных значениях параметризации вязкости для g =0.01 (рис. 5, б , в ). Графики 1, 2, 3, 4 на рис. 5, б соответствуют гипервязкости N =2 с коэффициентами K 21 , K 22 , K 23 , K 24 , графики 5, 6, 7 - турбулентной вязкости v =10¹², 10 13 , 10 14 см²с^-1. Графики 1, 2, 3, 4 на рис. 5, в построены для гипервязкости N =3 с коэффициентами K 3₁ , K 3₂ , K 33 , K 3₄ . На рисунке приведены также графики инкрементов для аномалий среднего потока с амплитудами g =0.02, 0.03 при коэффициенте гипервязкости K ₃₃.

Важной составляющей среднего потока является дифференциальное вращение. Расчеты показали, что зависимость баротропной неустойчивости от параметров дифференциального вращения является менее сильной, чем зависимость от параметров вязкости и меридиональной компоненты течений, однако вполне значимой. В табл. 1 приведены времена роста наиболее неустойчивых мод Q ₀ /Re( a ) при различных значениях параметров дифференциального вращения для амплитуды возмущения g =0.01, v =0 и при коэффициенте рэлеевского трения r ₁₀₀₀ , т. е. при условиях, наиболее благоприятных для развития баротропной неустойчивости. Во втором и четвертом столбцах таблицы приведены времена роста наиболее неустойчивых нормальных мод в оборотах Солнца ( T р ), в третьем и пятом столбцах – периоды колебаний этих мод ( Т ). Числа в круглых скобках – времена роста и периоды колебаний наиболее неустойчивых мод для амплитуды возмущений 0.005.

Так как условия для развития неустойчивостей были выбраны наиболее благоприятными, времена роста неустойчивости оказались очень небольшими, всего 2–4 оборота Солнца, причем дифференциальное вращение, независимо от значений параметров a и f, стабилизировало развитие неустойчивостей. Периоды колебаний изменялись в более широких пределах: от –58 до +25 оборотов Солнца. Более сильной оказалась зависимость инкрементов роста неустойчивых мод от конфигурации возмущений среднего потока. В табл. 2 и 3 приведены характери- стики неустойчивостей для возмущений среднего потока, имеющих структуру сферических гармоник с различными значениями n и m, для параметров дифференциального вращения a=0.3, f=0.5 и относительной амплитуды возмущений 0.01.

Для всех гармоник расчеты демонстрируют высокие скорости роста неустойчивостей при достаточно большом разбросе периодов нормальных мод. Уменьшение амплитуды возмущений среднего потока

Таблица 1

Характерные времена роста ( T _р) и периоды колебаний ( Т ) наиболее неустойчивых нормальных мод при задании возмущения среднего потока в виде сферической гармоники Р₆⁵ ( р ) cos5X и при различных параметрах осесимметричного дифференциального вращения a и f

f=0 f=0.9 a Tр Т Тр Т 0 2.33 (4.77) 11.33 (23.45) – – 0.1 2.48 (7.13) 11.77 (24.69) 2.4 (5.6) 11.6 (24.19) 0.2 3.05 (6.00) 12.1 (–23.66) 2.6 (5.21) 11.8 (–21.24) 0.3 3.64 (7.02) –15.29 (–15.62) 2.92 (7.31) 12.33 (–22.74) 0.4 3.57 (7.66) –13.06 (–58.25) 3.27 (5.89) 13.22 (–23.9) 0.5 3.54 (8.72) –11.34 (–11.3) 3.58 (6.69) 14.03 (–21.0) приводит к пропорциональному уменьшению инкрементов роста неустойчивостей.

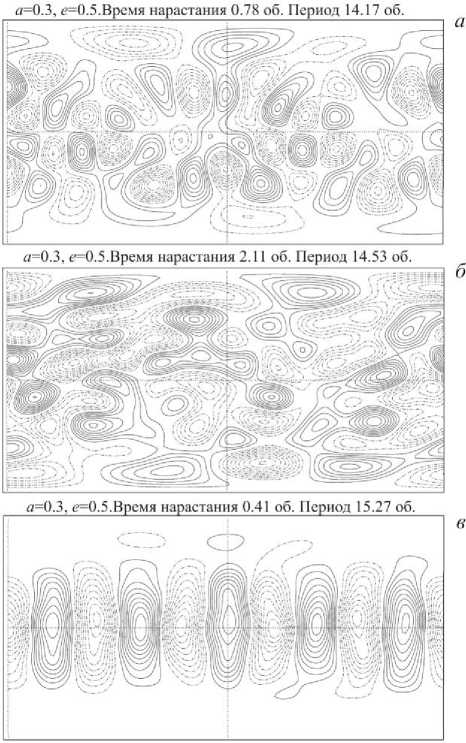
На рис. 6 представлены пространственные структуры наиболее неустойчивых нормальных мод для возмущений среднего потока, аппроксимируемых различными сферическими функциями. Как мы уже отмечали, при близких значениях инкрементов пространственная структура неустойчивых мод весьма изменчива и может существенно меняться при небольших изменениях среднего потока.

Влияние на устойчивость тахоклина возмущений толщины слоя. F 1 * 0, F 2 =0, F 3 * 0

В отличие от рассмотренного ранее оператора F ₂ , оператор F 3 , отвечающий за взаимодействие возмущений с аномалиями толщины слоя, является дифференциальным оператором первого порядка и в меньшей степени зависит от масштаба возмущений. При задании аномалии толщины слоя жидкости в виде сфери-

й=О.З, е=0.5.Время нарастания 0.78 об. Период 14.17 об.

а=0.3, е=0.5.Время нарастания 2.11 об. Период 14.53 об.

а=0.3, е=0.5.Время нарастания 0.41 об. Период 15.27 об.

Рис. 6. Пространственная структура наиболее неустойчивых нормальных мод при возмущениях среднего потока ψ , аппроксимируемых различными сферическими функциями: m =2, n =5 ( а ); m =5, n =7 ( б ); m =1, n =5 ( в ).

Таблица 2

Характерные времена роста Т _р и периоды колебаний Т наиболее неустойчивых нормальных мод при задании возмущения среднего потока в виде сферической гармоники, имеющей порядок m =5 и степени n =7–9

	n =7	n =8	n =9
Tр	2.11	1.79	1.19
Т	–102	–90.62	72.81

Таблица 3

Характерные времена роста Т _р и периоды колебаний Т наиболее неустойчивых нормальных мод при задании возмущения среднего потока в виде сферической гармоники, имеющей порядок m =2

	T р	Т
n =3	1.18	6.09
n =4	0.98	7.14
n =5	0.785	–14.17
n =6	0.864	–94.33
n =7	0.669	2182.18
n =8	1.025	269.64
n =9	0.96	–33.65

Таблица 4

Характерные времена роста Т _р и периоды колебаний Т наиболее неустойчивых нормальных мод при задании возмущения среднего потока в виде сферической гармоники, имеющей порядок m =1

	т T р	Т
n= 2	0.95	10.17
n =3	0.54	12.6
n =4	0.51	14.98
n =5	0.41	15.26
n =6	0.54	17.23
n =7	0.55	15.97
n =8	1.21	14.32
n =9	1.87	10.27

ческой гармоники производные, входящие в оператор F 3 , равны

d( Ih/h),

= 2Q h' cos m X x x<

д ц

V

¹ v ^{2 -} 1 )

[ ( n ^- ™ + 1 ) С ^{- (} n + 1 ) VP ] ⁺ P f^x (13

v d(lhT/hо)                          ™(\ x---------=-2Qh m sin ( m X ) цР ( ц ), dX

)

где h' = A/h - относительная амплитуда колебаний толщины слоя жидкости, Q - угловая скорость вращения аномалий толщины слоя. При оценках Q была принята равной угловой скорости дифференциального вращения на широте 30°.

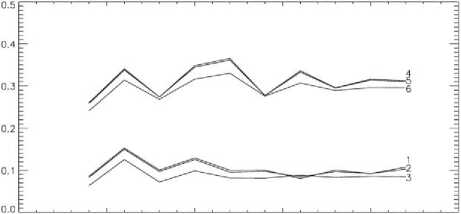
Зададим пространственную структуру вариаций толщины слоя в виде гармоники h'Р₆5 ( ц ) cos5X и рассчитаем характеристики нормальных мод. На рис. 7 приведены графики инкрементов роста наиболее неустойчивой нормальной моды в зависимости от числа гармоник в разложении функции тока для турбулентной вязкости с коэффициентами v =0, 10¹², 10¹³ см²с^-1 при h ‘ =0.1 и h ‘ =0.2. Параметры дифференциального вращения были приняты равными a = f =0.5. Кривые, построенные для различных параметризаций вязкости, практически совпадают, следовательно, турбулентная вязкость слабо влияет на развитие неустойчивостей, обусловленных вариациями толщины слоя. Характерное время развития

Инкременты, аномалии толщины слоя. Вязкость Л^1

5              10              15             20             25             30

максимальная степень в разложении

Рис. 7. Зависимости инкрементов роста наиболее неустойчивой нормальной моды от числа гармоник в разложении функции тока для турбулентной вязкости с коэффициентами v =0, 10¹², 10 13 см²с^-1для h' =0.1 (кривые 1, 2, 3) и h '=0.2 (кривые 4, 5, 6).

Таблица 5

Характерные времена роста Тр и периоды колебаний Т наиболее неустойчивых нормальных мод при задании возмущений толщины слоя жидкости в виде сферической гармоники P5 (ц) cos5X с амплитудами 0.2 и 0.1 и при различных параметрах осесимметричного дифференциального вращения a и f

	f =0		f =0.9
a	T р	Т	Т р	Т
0	3.57 (7.96)	–17.10 (–23.33)
0.1	3.90 (9.02)	21.96 (37.19)	3.84 (9.0)	–19.65 (50.92)
0.2	4.18 (15.21)	21.96 (28.36)	3.90 (9.42)	21.99 (36.88)
0.3	5.39 (27.55)	12.34 (42.48)	3.95 (12.41)	21.99 (35.40)
0.4	8.59 (22.99)	–36.05 (29.90)	4.36 (14.91)	15.56 (45.46)
0.5	13.20 (26.12)	-45.64 (59.78)	4.97 (14.59)	14.50 (36.34)

Таблица 6

Характерные времена роста Т _р и периоды колебаний Т наиболее неустойчивых нормальных мод при задании возмущений толщины слоя жидкости в виде сферической гармоники, имеющей порядок m =5 и степени n =7–9

	n =7	n =8	n =9
T р	2.44	1.71	1.33
Т	13.92	14.07	19.17

Таблица 7

Характерные времена роста Т _р и периоды колебаний Т наиболее неустойчивых нормальных мод при задании возмущений толщины слоя жидкости в виде сферической гармоники, имеющей порядок m =2

Tр Т n=3 2.91 12.02 n=4 1.59 11.66 n=5 1.10 14.80 n=6 0.82 17.51 n=7 0.68 31.54 n=8 0.54 38.02 n=9 0.47 58.31 неустойчивостей при h'=0.2 составило примерно 2-4 оборота Солнца, а при h‘=0.1 - 9-12 оборотов Солнца.

В табл. 5 приведены результаты расчетов инкрементов роста и периодов колебаний наиболее неустой-

Таблица 8

Характерные времена роста Т _р и периоды колебаний Т наиболее неустойчивых нормальных мод при задании возмущений толщины слоя жидкости в виде сферической гармоники, имеющей порядок m =1

т Tр Т n=2 2.28 14.56 n=3 1.29 17.19 n=4 0.89 17.65 n=5 0.77 20.45 n=6 0.65 19.59 n=7 0.65 21.99 n=8 0.61 20.86 n=9 0.67 22.53 чивых мод при различных значениях параметров дифференциального вращения и разной амплитуде возмущений для n=11 . Во втором и четвертом столбцах таблицы указаны характерные времена роста наиболее неустойчивых нормальных мод (в оборотах Солнца), в третьем и пятом столбцах – периоды колебаний этих мод для величины h'=0.2, примерно соответствующей относительной толщине слоя проникающей конвекции [Miesch, 2005]. В круглых скобках приведены времена роста и периоды колебаний нормальных мод для относительной амплитуды возмущений 0.1.

Так же как и в случае неустойчивостей, обусловленных вариациями среднего потока, дифференциальное вращение при всех значениях параметров a и f оказывает стабилизирующее влияние на развитие неустойчивостей. С увеличением разности скоростей полюс–экватор возрастает характерное время роста возмущений.

В табл. 6–8 приведены характеристики неустойчивостей для возмущений толщины слоя, имеющих структуру сферических гармоник с различными значениями n и m , для параметров дифференциального вращения a =0.3, f =0.5 и относительной амплитуды возмущений 0.2.

Для всех гармоник расчеты демонстрируют высокие скорости роста неустойчивостей. Уменьшение амплитуды возмущений толщины слоя приводит к пропорциональному уменьшению инкрементов роста неустойчивостей.

Обсуждение

Расчеты характеристик неустойчивости с помощью квазигеострофической баротропной модели показали, что возмущения горизонтальной структуры среднего потока и неоднородности толщины слоя тахоклина приводят к дестабилизации течения во всей области параметров осесимметричного дифференциального вращения. Темпы роста неустойчивостей зависят от амплитуды и горизонтальной структуры возмущений среднего потока. Для возмущений толщины слоя и структуры среднего потока, аппроксимируемых сферическими функциями при достаточно реалистичных амплитудах возмущений, характерный временной масштаб роста неустойчивостей составляет несколько оборотов Солнца, что намного меньше времени роста неустойчивых нормальных мод осесимметричного дифференциального вращения. Такие характерные времена роста неустойчивостей уже сопоставимы с типичными временными масштабами процессов формирования активности на Солнце. К сожалению, данные глобальной гелиосейсмологии не дают информации о реальной структуре тахоклина, поэтому приведенные выше результаты численных экспериментов следует считать лишь предварительной оценкой возможности подобного механизма развития неустойчивостей. Для более точных оценок необходимо учитывать также нелинейность процессов и магнитное поле в тахоклине.

Выполненные расчеты иллюстрируют важную роль учета крупномасштабных течений в исследовании динамики тахоклина. Эти течения могут быть следствием внешнего воздействия, например проникновения в верхние слои Солнца реликтового поля, либо следствием проникновения в тахоклин меридиональной циркуляции и/или магнитного поля из области конвекции. Так как течения в тахоклине, в отличие от слоя развитой конвекции, преимущественно горизонтальны, неустойчивости способны передавать энергию в направлении более крупных масштабов – свойство, характерное для квазигео-строфических двумерных течений, например, в земной атмосфере. Поэтому в тахоклине естественно ожидать формирования крупномасштабных вихрей и накачки длинных волн Россби. Возможно, наблюдаемые в фотосфере низкочастотные колебания солнечной активности являются следствием такой накачки.