Гидродинамический расчет упорного подшипника скольжения с нежесткой опорной поверхностью, работающего на микрополярной смазке

Введение. Как известно [1-3], микрополярная жидкость широко используется в качестве модели гидродинамической смазки в узлах трения машин и механизмов. Анализ существующих работ [4-6], посвященных гидродинамическому расчету упорных подшипников скольжения, работающих на микрополярной смазке, показывает, что во всех этих работах опорная поверхность подшипника считается абсолютно жесткой.

В области подшипников, работающих на микрополярной смазке, появилось новое направление – подшипники с нежесткой опорной поверхностью. В данной работе рассматривается установившееся движение микрополярной смазки в зазоре упорного подшипника с податливой опорной поверхностью (рис.1).

Рис.1. Схематическое изображение упорного подшипника: 1 – недеформиро-ванный контур, прилегающий к смазочному слою; 2 – деформированный контур; 3 – недеформированный контур, прилегающий к жесткой опорной поверхности подшипника; 4 – упругий слой

В качестве исходных уравнений берется система безразмерных уравнений движения мик-рополярной жидкости для «тонкого слоя»:

d2v

d ² u      dv   dp

+ N¹

d y      d y  dx dy

ν

-

N i

-

1 du   . du du   .

--= 0,  — + — = 0.

N 1 d y        d y d x

Здесь размерные величины u ‘ , u‘ , v‘ , y ‘ ,p' связаны с безразмерными u , u , v , y,p соотношениями:

(2ц. X ) Lu

u = u u, u = u eu, v =v v, y = hy, p = p p, x = Lx, p =----------

⁰                                2 h 0

„ ho_

^{, 6} L ’

v * -    , N ' , N - ¹² , l =^L ,

2hо       2ц + %   1 h02 %      4ц где и', o' - компоненты вектора скорости; p' - гидродинамическое давление в смазочном слое; V' - вектор скорости микровращения; ц - коэффициент вязкости для ньютоновской жидкости; Y, X - коэффициенты вязкости микрополярной жидкости; L - длина ползуна; h0 - толщина пленки в начальном сечении, без учета деформации.

Система уравнений (1) решается при следующих граничных условиях: и --1, и- 0, V- 0 при у - 0, и -0, и-0, V-0 при у - 1 + nx + П1Ф(x),

Р ^{(0) -} Р ^{(1) -} Pa / Р\                                      ⁽²⁾

Ltgа X'    z ч rf x') А x')                                                    „ где п- ——, п1 - —, ф(x) - f I — I, Xf I — I - функция, характеризующая деформацию упру-h 0        h0           V L/ V L/ гого слоя на поверхности ползуна.

К системе уравнений (1) необходимо добавить следующую безразмерную систему уравнений Ламэ для «тонкого слоя»:

d ² Uy д у *²

- 0,

д ² u_x д у *²

- 0.

Здесь в упругом слое переход к безразмерным переменным осуществлен по формулам:

у '- h ₀ + ( h ₁ - h ₀ ) у * , и у . - и и _у , и x. - u u _x , x '- L • x ,                       (4)

где иу, и иx. - компоненты вектора перемещений; и - характерная величина компонент вектора перемещений; 5* - h1 - h0 - толщина упругого слоя.

В переменных (x, y) и (x, y*) уравнение недеформированного контура опорной поверхности, прилегающей к смазочному слою, можно записать в виде у -1 + п x - H 1( x), у *-П2 x - H 2( x), П2 - Ltgg^.                     (5)

о

Уравнение контура внешней поверхности упругого слоя в переменных (y*, x) запишем в виде:

у * - 1 + ц ₂ x - H ₃( x ).

Система уравнений (3) решается при следующих граничных условиях:

д и, N —г д у ^*

(1 + а ) Gu h_n Здесь M -      *—^°;

(1 -а ) о р

- ди I         м диу I у" - H 2 ( x ) - ду I у- H1 ( x ) ,       ду * । у" = H 2 ( x )

и x

N -

| у * - H з ( x )"

и h ₀ G

»_е» ;

ц ₀ и о

- 0, U_v . „ , = 0. ^у|у ^- H з ⁽ x )

-

Р ,

G - модуль упругости; а * - постоянная

Мусхели-

швили. Для микрополярной смазки обычно N 1 >>1.

Полагая 1/N1 -е<< 1, асимптотическое решение системы (1), удовлетворяющее граничным условиям (2), будем искать в виде: ю                        to                        to                        to1

и -Еukеk, и-Еиkеk, v-Zvkеk, р-ZPkek,e-tt.(8)

k-0              k-0              k-0               k-0

Подставляя (8) в (1) и (2) для нулевого приближения (соответствующего ньютоновской

жидкости), придем к следующей системе уравнений и граничных условий к ним:

д ² и ₀

д у ²

dp о ^ди о + ^{д и} о = о dx ’ д у   д x

^и о =

— 1, и ₀ = 0 при у = 0; и ₀ = 0, и ₀ = 0 при у = h ( x ) = 1 + n x .

Точное автомодельное решение задачи (9)-(10) будем искать в виде:

^и о ^=дГ ° ⁺ U ⁽ x , У ), ^и о = ^—^т ^{0 +} V ⁽ x , У ), д у                 д x

dp ₀

—

■——

dx

= c 1 + С - 2

h 2     h 3 ,

V о

^^

-——

~

= ¥ о ( 5 ), U 0 = и о ( 5 ), V = и ( 5 ) h ' .

Подставляя (11) в (9) и (10), придем к следующей системе обыкновенных дифференци-

альных уравнений и граничных условий к ним:

——

т

-——

~

"

—

~

'

~

— '

V о

V 0

= c 2 , и о

= ^С 1 ,

~

и о — 5 и о

~

'

= 0 ;

= 0 при 5 = 0, 5 = 1; и о = — 1, и о = 0 при 5 = 0;

~

~

и о = о, и о = о при 5 = 1; J и ₀ ( 5 ) d 5 = 0.

Решение задачи (12)-(13) легко находим непосредственным интегрированием. В результа-

те будем иметь:

-—-

V о' = £2 (52 — 5)

—

~

— 5 ²

—

—

где с 1 = — 6.

, и о = с, —

,           12

—

c ₁

—

к

л

1 5 — 1,

у

Безразмерное гидродинамическое давление определяется из уравнения

dp ₀

—

-——

dx

_ c i + c 2

h ²     h ^{3 .}

Перейдем к решению задачи для первого приближения.

Из системы (1), с учетом (8) для первого приближения, придем к следующей системе

дифференциальных уравнений и граничных условий к ним:

д2и.       дv1   dp ди.   ди.

—1- + N ²—¹ =— , —¹ + — ¹ = 0, д у ²       д у   dx  д у   д x

лучим:

д ² v ₁

д у y

д и,

д r

—"

———

£ = V 0 + и 0_ = ^С 2 Г 2 y h ² h   2 h ² к h

—

1 |+ 1

J h

— у 1 h

—

( —

£ 1

к ²

—

\

,

V.

и 1 = 0, и 1 = 0, V 1 = 0 при у = 0; и 1 = 0, и 1 = 0, V , = 0 при у = h ( x ).

Решение задачи (16)-(17) находим непосредственным интегрированием. В результате по-

———

V1 =

c ₂

( У ³

2 h ²

и1 =

—

у ² )

к 3 h

dp y ²

—

у

+ — h

———

dx 2

N ²

1^ 2 | 2 h

f

c

— у-

1 6 h

—

С1

к ²

—

у

у

———

—

f

y ⁴

—

у ³ )

c

c

+     ² + -1-

к 12 h

—

? у ; 2 у

к 12 h

—

c

+ —2+-1-

—

у

+ — h

к 12 h

1 ) у

—

² у ²

С1

c ^y

¹ 24 h

—

—

—

к ²

у

+

dp hy N ² h

12 ^{y .}

dx 2

—

Интегрируя уравнение неразрывности от 0 до h для определения гидродинамического давления, приходим к следующему уравнению

2 ~    Г? ~ dpL = - ^£1 — NA + с.                      (19) dx    60 h 60 Для интегрирования уравнений (15) и (19) необходимо вначале найти функцию ф(x). Ин- тегрируя систему уравнений (3) с граничными условиями (7), будем иметь: pp и . =у +—H. (x). у   M M 3 Воспользуемся приближенным равенством Г - Г ~ и А •                                        (20) 1 д      «I      у \у = H2(x) ’                                                                     4 7 где rд – уравнение деформированного контура опорной поверхности; rн – уравнение недеформи-рованного контура.

м                              < х Ро +е Pl п         е Р1    Ро       к                . Из (20) следует, что п,ф ( x ) ~ ———• Полагая — << — для безразмерной функции м    ММ

П 1 ф (х), характеризующей деформацию опорной поверхности, получим следующую приближенную формулу:

	W( x ) ~ Р 0 / M.                               (21) Из уравнения (15), с учетом (21) для определения р 0( х ), приходим к следующему уравне-
нию	dp o _        c i                c 2 = Г             к2 1                А3 •                                 ( ) dx I 1            Р о I I 1            Р о I 1 + п x + —      1 + П x + (     M JI     M J

Решение уравнения (22) находим в виде ряда Тейлора в окрестности точки x =0.

P 0 = P 0(0) + Р ‘ (0) x + Р(0) x2 +...,                         (23) где Р0(0) = Р.. р‘(0) =  ---c      + -—c2-—3; p 1 1 + — pa 1   |1 + — Рг 1 ( M р J  ( M р J 2с U   0 (0) I   зг      0 (0) I 2 £ П +          3 С? П + M       M Р 0(0) =   ,         . 3       и         V                          (24) |1 + РУ |        |1 + Ра | ( M р J     (  M р J и т.д. Р "(0) Константа c2 определяется из условия p0(0) +      = 0. Решение уравнения (19) также находим в виде (23): 2 Р1 = Р1(0) + Р‘(0) x + p‘(0)   +...,                                 (25) 22 где Р1(0) = 0, p‘(0) =.-----2---. - —-1 + c; 1 р 1    60 601 1 + — Р* 1 ( M p J p1"(0) =

N ² c ₂

(л+ Mp ЛО) J

60 < in?

11+p I

I M p J

•

Константа с определяется из условия p ‘ (0) + p ‘ (0)1 = 0.

Таким образом, с учетом (23) и (24) для безразмерной несущей способности подшипника, получим следующее выражение:

4- = p 0 (0)1 + p j (0)l + _e p L 2      6

p ‘ (0) ₊ p ‘ (0) 2      6

,

где p 0 (0), p ‘ (0), p ‘ (0) определяются выражениями (24) и (26).

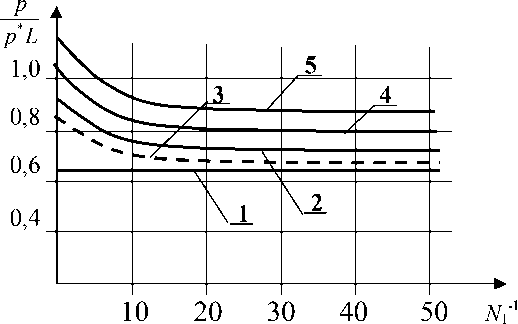
Рис. 2 Зависимость безразмерной несущей способности от параметра N 1 ^-1 при различных значениях параметров М и N : 1 - M ^ да , N ^{- 1} ^ да ;

2 - N ² = 0,6, N ^{- 1} = 40, M ^да ; 3 - N ² = 0,6, N ^{- 1} = 40, M = 100 ;

4 - N ² = 0,8, N ^{- 1} = 40, M >/ ; 5 - N ² = 0,9, N , ^{- 1} = 40, M ^да

Результаты численного анализа найденного аналитического выражения (27), приведенные на рис.2, показывают:

• 1)    при заданных значениях безразмерного параметра связи N , присущего микрополярной смазке, и значения упругогидродинамического параметра М , с увеличением безразмерного параметра N 1^-1 , также присущего микрополярной смазке, несущая способность уменьшается. В предельном случае, при N ₁ ^-1 ^да , значение несущей способности стремится к соответствующему значению несущей способности подшипника, работающего на ньютоновской смазке;

• 2)    при заданном значении упругогидродинамического параметра М , с увеличением значения параметра связи N , несущая способность подшипника возрастает. Наиболее резкое увеличение несущей способности достигается при значениях N ²е [0,6;0,9];

• 3)    несущая способность подшипника при заданных значениях параметров N и N 1 слабо зависит от значения упругогидродинамического параметра М . С увеличением значения параметра М несущая способность подшипника возрастает, оставаясь меньше от соответствующего значения несущей способности подшипника с жесткой опорной поверхностью.

Выводы. Разработан метод расчета упорного подшипника скольжения с нежесткой опорной поверхностью. Дана оценка влияния значений безразмерных критериев, присущих микрополярным жидкостям, а также упругогидродинамического параметра на основные рабочие характеристики подшипника. В результате установлено, что с увеличением значения параметра связи N несущая способность подшипника возрастает. Деформация опорной поверхности подшипника незначительно влияет на его несущую способность.