Гидродинамика потока вязкой жидкости в решетке профилей лопаток центробежной гидромашины

Из анализа различных схем обтекания лопаток центробежных насосов (ЦБН) [1; 2] рассмотрим схему малорасходного режима, когда точка раздвоения линии тока совпадает с угловой точкой Е (рис. 1, поз. II), в которой пересекаются входная и боковая кромки профиля лопатки.

Поток в каналах рабочего колеса (РК) ЦБН формируется при обтекании входных кромок лопаток, имеющих конечную толщину δ _л с прямой формой входной кромки или в виде клина длиной l _кл ≤ 10 мм, величиной σ ₁ ≤ 2 мм, образуемой в результате пересечения лопатки с окружностью входа в РК радиусом R 1 и углом установки β 1л средней линии профиля лопатки. На напорной стороне лопатки пограничный слой не только определяется характеристиками набегающего потока, но и оказывает на него обратное влияние через толщину вытеснения δ*, что приводит к изменению гидродинамического угла установки лопатки от геометрического на величину ∆β л (рис. 2).

Оценим влияние вытесняющего действия пограничного слоя в области входа на лопатку. С учетом толщины вытеснения пограничного слоя набегающего потока, угол натекания гидродинамического потока вязкой жидкости значением угла натекания потока составит:

δ ^*

β=β1л + arctg . (1) lкл где δ* – толщина вытеснения, которую можно оценить, используя известные из теории пограничного слоя соотношения при обтекании с градиентом давления [3].

Следует отметить, что конечная толщина лопатки и параметры ее входной кромки не только формируют поток на входе в межлопаточный канал, но и оказывают на него подтормаживающее действие за счет силы реакции F и стесняющее – за счет конечной толщины лопатки δ _л с учетом суммарной площади лопаток на входе.

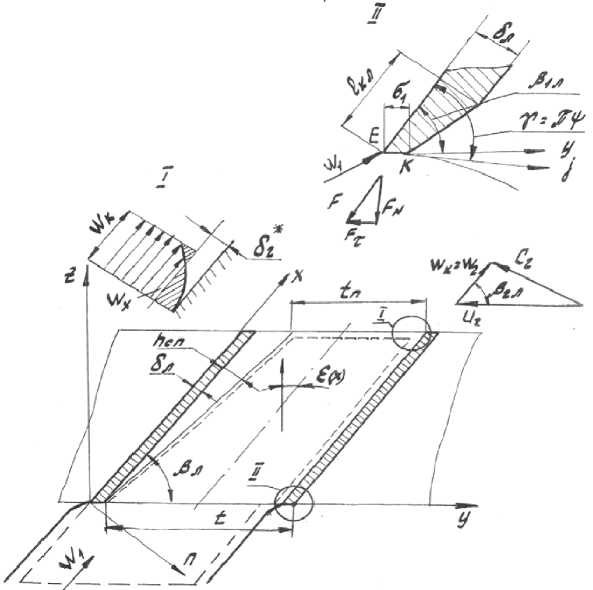
Рис. 1. Расчетная схема обтекания решетки прямых профилей

Полную силу F , действующую на поток со стороны кромки, можно разложить на две составляющие: F N - нормальную к входной кромке и F _T - касательную, которая представляет собой силу трения, определяемую вязкостью жидкости. Сила F N рассчитывается по закону распределения давления вдоль входной кромки лопатки величиной л :

где С и m - постоянные величины,

Ψγ m =      =       .2-Ф 2л-у

При совпадении входной кромки с осью Y (y = в 1л ):

m=

л

F n = J Pdj .                 (2)

в 1л

2п — в1л .

Тогда для клина с углом раствора пу и длиной одной стороны входной кромки лопатки равной л при j = л ; W j■ ) ~ W K из уравнения (3) получим:

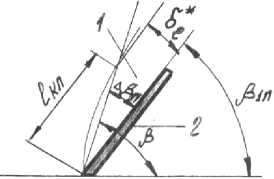
Рис. 2. Расчетная схема угла натекания потока на лопатку: 1 - пограничный слой; 2 - лопатка

W

C = W K ;

Л

и запишем уравнение (3) следующим образом:

Wj ) = W^j m .

л

Рассмотрим, следуя авторам работы [1], обтекание лопатки с входной кромкой, которая может не совпадать с фронтом решетки, как обтекание окрестности передней критической точки клинообразного тела с углом раствора у = пу. Согласно [3], скорость потенциального течения в ядре потока вдоль входной кромки будет иметь вид

Решение уравнения пограничного слоя проводим с учетом градиентного обтекания лопатки, принимая согласно [4], что по всей длине входной кромки л ₁ пограничный слой ламинарный. Для оценки закона изменения толщины потери импульса о вдоль входной кромки лопатки используем выражение из работы [3], сведенное к простой квадратуре:

W j ) = C m ,

^{2    0},^{47 v}

( ^О 1 ) = J W ) dj .                 ⁽⁸⁾

W ( j ) 0

Откуда, с учетом (7), имеем

5 ** = 0,686

G m V j ⁽ 1 - m )

\ Wk (5m +1).

Используя табличную функцию f 1 (æ), предложенную

Г. Хольштейном и Т. Боленом [3], принимаем

f . ($) = |*r ,

тогда изменение толщины вытеснения пограничного слоя 5* вдоль входной кромки лопатки запишем в виде

Для широкого диапазона изменения параметров рабочих тел с вязкостью ν = 0,5∙10^–6…1∙10^–4 м²/с проанализируем реальность перехода ламинарного пограничного слоя в турбулентный для РК с углом в _1л = 30°; угловой скоростью ω = 800 рад/с и относительной скоростью потока W ₁ = 3 м/с. Течение у входной кромки лопатки длиной 7 1 и вдоль ее напорной поверхности принимается эквивалентным обтеканию клина с углом раскрытия γ (рис. 1, поз. II).

Расчет устойчивости течения рассмотрим для профиля скоростей, рассчитанных способом К. Поль-гаузена с формой профилей, определяемых безразмерным параметром [3]:

5 * = f . ( $ ) 5 ** ,                  (11)

где значение формпараметра æ запишем следующим

5 2 W

V dy ,

образом:

( 5 ** ) 2 dW^      m

$ v "  dj    ( 10,64 m + 2,128 )"

зависимость которого от критического числа Рей-

нольдса определяем по толщине вытеснения пограничного слоя:

Для постоянного угла заострения входной кромки лопатки γ = πψ из выражения (12) видно, что f ₁(æ) не изменяется вдоль всей входной кромки.

На примере конкретных РК ЦБН для входной кромки решетки профилей лопатки, касательной к окружности входа РК в точке Е (у = Р _1л), проведены расчеты изменения параметров пограничного слоя: толщины вытеснения 5 * и толщины потери импульса 5 ₁ вдоль кромки лопатки в зависимости от значения относительной скорости набегающего потока W_y .

Рассчитанные по уравнению (7) значения изменения относительной скорости потока при обтекании решетки профилей с клином входной кромки РК параметров: R ₁ = 8,25 мм, R ₂ = 20,25 мм, шагом решетки t 1пр = 14,95 мм и ширины b 1 = 4,3 мм приведены на рис. 3 для трех значений углов установки лопатки в _1л = 18°; 30° и 40°. Скорость потока W y вначале резко возрастает до 60…80 % на длине, составляющей 10 % всей кромки, а затем медленно увеличивается, достигая на остальной длине значения W K . При этом следует отметить, что с ростом угла установки профиля темп нарастания скорости W_y уменьшается.

Re

кр 5

^w ( y )⁵ *

V

При значении Re ₅ * > Re ₅ * ламинарный погранич-

ный слой переходит в турбулентный.

Между безразмерными параметрами æ (формула (12)) и Л существует известное универсальное соотношение [3]:

37 Л Л ²

315 945 9072

$ = Л

Для входной кромки лопатки с углом в _1л = у = 30° расчеты по приведенным выше зависимостям дают m = 0,0908, тогда æ = 0,029, что соответствует Л = 2,243 и f , ($) = 2,457.

Имеем, что Re_к р ₅ * = 2,65^10 3 (рис. 17.3 работы [3]).

Толщину вытеснения для конца участка клина (j' = 7 1 ) оценим по выражению (9) и с учетом (10) получим

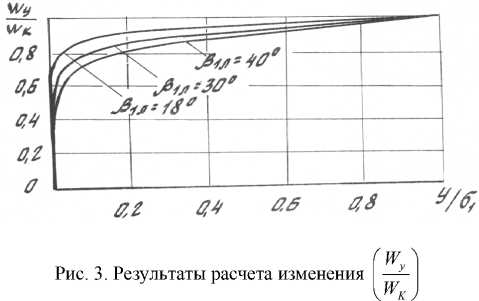
на входе решетки профилей лопаток

0,5

I VO. I

5 1 ( 30 ° ) = 1,398 1^7 1 I                    (16)

\ W K )

или

Re * = W K ⁵. = 1,398 Г W K ⁷ Y.       (17)

⁵ v I v J

На основе анализа расчетной величины формпараметра (æ), в зависимости от m , в практическом диапазоне изменения углов установки лопатки от 18 до 40° рассмотрим влияние на толщину вытеснения пограничного слоя и значение Re 5 * . Из дальнейшего анализа для принятого угла в _1л = 30° при Re ₅ * = 2,65^10 3 и входной кромки 7 1 =2 мм, получим: для воды (ν = 1∙10^–6 м²/с) W K = W K кр = 1598 м/с; для глицерина (ν = 1∙10^-4 м²/с) W K = W K кр = 1598 ∙10² м/с. Следует отметить, что расчетные значения относительной скорости, при которой реализуется переход к турбулент-

ному пограничному слою, на три и более порядков выше реальных значений W K по всей длине решетки профилей лопаток исследуемой центробежной гидромашины с параметрами: ст , = 2 мм и l _пр = 18,6 мм для вышеприведенных значений РК ( Р _1л = 30°; Р _2л = 70°) ЦБН, работающего на ряде рабочих жидкостей. Расчетные значения изменения параметров толщины вытеснения 5 * и толщины потери импульса 5 ** пограничного слоя вдоль рабочей решетки профилей лопаток центробежной гидромашины приведены на рис. 4 для ряда рабочих жидкостей: вода (v = Ь10^-6 м²/с; р = 10³ кг/м³), глицерин (v = 1,18-10^-3 м/с; р = 1,26^10 3 кг/м³), водный раствор глицерина (v = 10 " ⁴ м 2 /с; р = 1,23-10³ кг/м³), Л3-ТК-2 при t = +20 °С (v = 0,7-Ю Г ⁶ м²/с; р = 691 кг/м³) и при -100 °С (v = 1,55-10^-5 м²/с; р = 784 кг/м³).

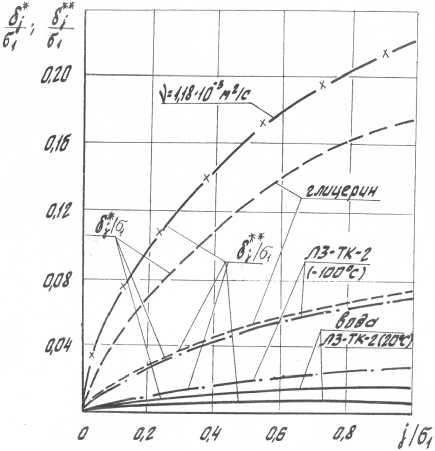
Рис. 4. Изменение параметров пограничного слоя вдоль рабочей решетки профилей по входной кромке лопатки

Из графиков видна существенная зависимость роста 5 * и 5 ** с увеличением вязкости рабочей среды. Так, при течении глицерина на кромке лопатки величина толщины вытеснения 5 ** составила 22,5 % от длины входной кромки о 1 . При этом от носика входной кромки значение 5 * вначале резко возрастает, достигая для всех рабочих жидкостей на половине длины кромки 75 % своего конечного значения.

Следует отметить, что проведенный анализ и расчеты параметров пограничного слоя в каналах РК МН проводились на основе приближенного решения уравнений пограничного слоя, предложенного К. Польгаузе-ном [3]. Обтекание входной кромки лопатки рабочей решетки профилей принималось эквивалентно обтеканию потоком вязкой жидкости окрестности передней критической точки клина с углом раскрытия у. При анализе пограничных слоев на каждой из поверхностей канала решетки РК пренебрегалось эффектами, связанными с течением в углах. Такое до- пущение при течении в геометрически диффузорном канале общепринято [2] и позволяет моделировать реальную ситуацию с достаточной точностью.

Очевидно, что качество приближенного расчета будет зависеть от степени точности выбранного распределения профиля скоростей:

W ( z ^

Wf [s ( z ) J= f ⁽ⁿ⁾ •

z где ц = - безразмерное расстояние от стенки, 5( z )

полученное делением размерной величины расстояния z по нормали от тела на толщину пограничного слоя 5 ( z ) . Сама функция f ( ц ) зависит только от п, чем выражается предположение об аффинности профилей скоростей [3].

Приближенный метод расчета параметров пограничного слоя в решетке профилей лопаток центробежной гидромашины имеет допущения, связанные, в частности, с расчетом не каждой отдельной струйки потока, а решения дифференциальных уравнений пограничного слоя только по средним его параметрам. Приемлемость подобного приема можно проверить, выполнив для сравнения (точные) автомодельные решения уравнений пограничного слоя. Известно, что рассмотренные классы течения имеют аффинноподобные профили скоростей, что позволяет выполнить точные решения уравнений пограничного слоя, так называемые автомодельные решения. Точное решение задачи осесимметричного течения для рассматриваемого случая обтекания клина в решетке профилей выполнил Д. Хартри. В работе [1] при анализе течения около передней точки клиновидного тела для двух значений Y = 0; ( m = 0) и у = 36°, ( m = 0,11) (см. формулу (4)) показано практическое совпадение профилей скорости, полученных при точном и приближенных решениях. Полученные решения позволяют с достаточной точностью определить силы трения и гидравлические качества РК ЦБН с учетом реальной гидродинамической картины течений потока вязкой жидкости в решетке профилей лопаток центробежной гидромашины.