Гидромеханические и информационные аспекты гравитационного моделирования протяженных объектов

ВВЕДЕНИЕ. ПОСТАНОВКА ЗАДАЧИ

Гравитационное моделирование (ГМ), под которым понимается применение искусственной силы тяжести (ИСТ) к исследованию природных и рукотворных объектов, нашло широкое применение в различных предметных областях. Примерами служат испытания и тарировки приборов ответственного назначения (центробежные стенды), исследования прочности объектов в строительстве и горном деле, отбор и подготовка экипажей скоростных самолетов и космических аппаратов, лечение больных травматологического и неврологического профиля и т. д. Планируется применение ИСТ в Космосе в качестве инструмента научных исследований и противодействия невесомости, что важно для успешного выполнения длительных и сверхдлительных полетов, включая межпланетные миссии [1] - [5].

На рис. 1 представлены структуры ЕСТ (Земля, Марс, Луна) и ИСТ, генерируемой короткорадиусной центрифугой (ЦКР). Здесь: +Gz – модуль перегрузки, создаваемой ИСТ и ЕСТ; z – продольная координата, отсчитываемая, соответственно, от поверхности планеты или оси вращения; h – протяженность объекта в направлении oz; щ – угловая скорость вращения ротора ЦКР, где ® 1 < to 2 < to 3 .

Как видно, адекватность в форме баланса перегрузок достигается только в точках пересечения характеристик: горизонталей (ЕСТ) и се-мействанаклонных to i (ИСТ). В остальных точках баланс отсутствует, причем по мере их удаленности рассогласование только возрастает. Следовательно, ЦКР осуществляет адекватность, которую можно классифицировать как весьма условную, точечную.

В связи с условностью адекватности следует различать две группы объектов ГМ: точечные и распределенные. Под точечными (ТО) понимаются объекты, размеры которых столь малы по сравнению с радиусом вращения, что внутренним перепадом перегрузок можно пренебречь и считать поле ИСТ однородным. Если же размеры объектов соизмеримы с радиусом, то перепад становится значительным, и такие объекты далее отнесены к категории протяженных (ПО). Как следует из рис. 1, а для этого достаточно проанализировать изменение +Gz на интервале z/h = [0, 1], относительная величина перепада перегрузок в ПО достигает 100%.

Отметим, что переход по схеме “ТО - ПО” сопровождается следующими качественными изменениями. Во-первых, величина и точка при-

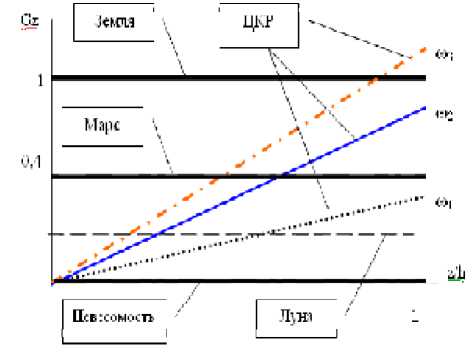
Рис. 1. Структурные различия ИСТ и ЕСТ ложения перегрузок при ГМ становятся неопределенными. Во-вторых, перегрузка утрачивает критериальные функции и переходит в разряд промежуточных параметров. В-третьих, процедуры оценки адекватности усложняются. Вследствие перечисленных и им подобных факторов информационное обеспечение ГМ, построенное на “точечной” идеологии, становится недостаточным. Особую актуальность приобретает комплекс задач по разработке методологии, ориентированной на оценку и обеспечение адекватности ИСТ и ЕСТ применительно к ПО.

В качестве решения указанной задачи предлагается проблемно-ориентированная автоматизированная информационная система по оценке адекватности (АИСОА) [6-8]. В целях сокращения изложения ограничимся анализом структурной схемы АИСОА (рис. 2), краткой характеристикой решаемых задач и математических моделей, представленных в конечной форме и реализованных в АИСОА. В качестве объектов ГМ выбрано весьма представительное подмножество ПО, содержащих протяженные гидравлические тракты [6].

КОНЦЕПЦИЯ АИСОА

В основу концепции АИСОА положен принцип воспроизведения состояний объектов, а не параметров векторного поля ЕСТ. Предусмотрено, что на этапах, предшествующих ГМ, такие параметры определяются методом компьютерного моделирования. Кроме того, учтено, что в ряде приложений в сеансах вращения принимает непосредственное участие человек (космонавт, испытатель, пациент гравитационной терапии). Это потребовало разработки мер по обеспечению параметрической безопасности. В итоге АИСОА приобрела двухуровневую иерархическую структуру, объединяющую в себе три функциональных компонента: физическое моделирование, т. е. соб- ственно ГМ (см. уровень I, рис. 2), математическое моделирование, обеспечивающее ГМ входными данными (поз. 3), и информационную поддержку принятия решений (поз. 4), образующие структуру, обозначенную как “Уровень II”.

Серия задач моделирования, названных, исходя из математического смысла, прямыми (поз. 3.1), заключаются в оценке адекватности ИСТ и ЕСТ (сходства, степень различий). Обратные задачи (поз. 3.2) состоят в определении индивидуализированных режимов испытаний, обеспечивающих либо минимум отличий, из числа возможных (поз. 3.2.1), либо заданные, причем разнонаправленные рассогласования (поз. 3.2.2). Как прямые, так и обратные задачи решены в 2-х постановках: интегральной и локальной (см. ниже).

ПРЯМЫЕ ЗАДАЧИ МОДЕЛИРОВАНИЯ В ИНТЕГРАЛЬНОЙ ПОСТАНОВКЕ

Указанные задачи решаются с помощью критерия адекватности вида [6], [8]:

5=-2---1--100%.       (1)

• - i

Здесь - _t , - 2 - приращение потенциальной энергии жидкости, заключенной в гидравлическом тракте объекта, обусловленное действием силы тяготения и центробежной силы соответственно.

В качестве обоснования правомерности предлагаемого подхода укажем на два обстоятельства. Известно, что именно жидкие среды в наибольшей степени откликаются на изменение гравитационной нагрузки. Кроме того, одним из фундаментальных положений аналитической механики (АМ) является положение об эквивалентности сил гравитации и центробежных сил инерции. К числу его проявлений относится линейная зависимость сил от массы [9]. Модели, применяемые в АМ, после некоторой модификации позволяют определить величины S_i . После их подстановки в (1) получим

• 5 = (ffl2 h3-R?(3h-2R1)-I)-ioo%. (2) Звд    (h - Rt)

Здесь: β – безразмерный коэффициент, учитывающий многообразие видов ЕСТ (Земля, Марс, Луна, др. варианты). β = a / g, где а, g -ускорение свободного падения, соответственно, на одной из планет и на Земле. Остальные обозначения и упрощенный вариант расчетной схемы приведены на рис. 3.

Таким образом, физический смысл критерия (2) состоит в сопоставлении энергии, полученной жидкостью, заключенной в объекте, как со стороны естественной, так и искусственной гравитации (эффект бустера) [6] – [8].

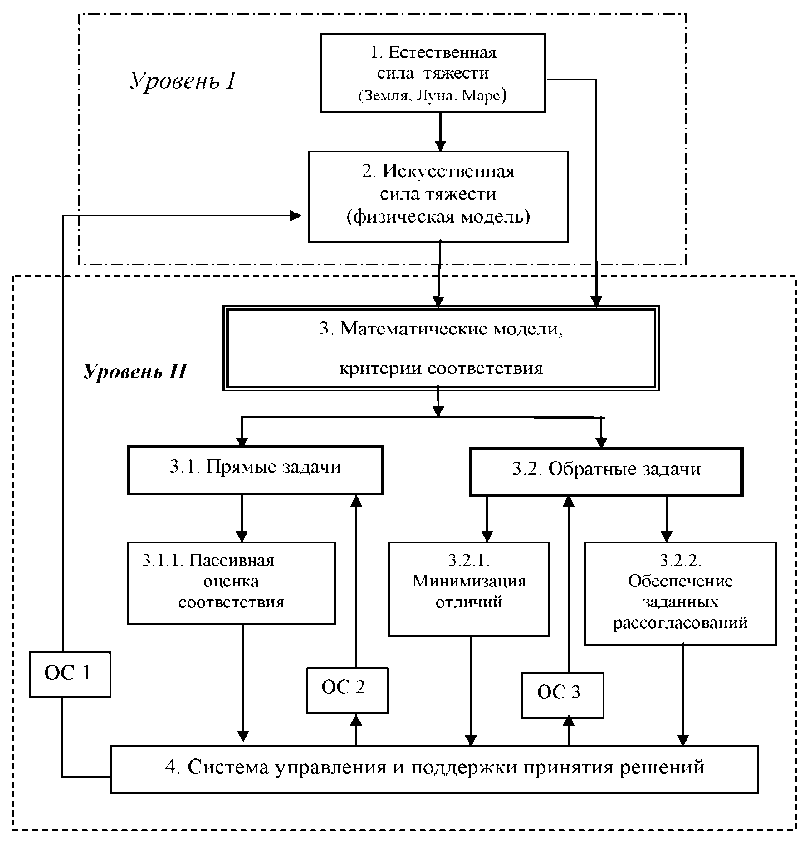
Рис. 2. Структурная схема АИСОА для оценки адекватности ИСТ и ЕСТ

Возможны три случая, отличающиеся величиной и знаком 5 . Если 5 = 0, имеет место адекватность, под которой понимается минимум отличий из числа возможных, оценивая их с энергетических позиций. Если 5 < 0, ЦКР сообщает объекту меньше энергии, чем ЕСТ, а если 5 > 0, соотношение изменяется на прямо противоположное.

Отметим следующие наиболее важные моменты. Во-первых, моделирование по формуле (2) означает пассивную оценку, т. е. регистрацию состояний ПО, при заданных испытателями параметрах всей системы, включая ЦКР и объект ГМ.

Во-вторых , в (2) учитывается распределение жидкости и ее “энерговооруженность” на всем протяжении гидравлического тракта, что и послужило основанием для названия – “интегральная оценка”.

В-третьих, перегрузка +Gz переместилась в категорию промежуточных параметров и, что особенно важно, в частный случай предлагаемого критерия (2). Последнее утверждение следу-max ет из (2) при R1 = 0 : 5 = (—3-^--1)100%.

Здесь + G™ = _ю ² h / g - перегрузка на периферийном радиусе z = h (см. рис. 3).

Следует обратить особое внимание на то, что при отсутствии полноценного критерия адекватности ИСТ и ЕСТ, параметр + G™ нашел самое широкое применение в различных приложениях, в том числе, космических [1 - 3].

Модель (2) реализована в блоке 3.1.1 АИСОА (рис. 2) с визуализацией результатов на экране ПК в виде типового окна (рис. 4). Особо отметим, что предлагаемый интерфейс обеспечивает режим массового решения задач по оценке адекватности ИСТ и ЕСТ, что важно с точки зрения практической значимости с учетом множества ПО и множества предметных областей.

ОБРАТНЫЕ ЗАДАЧИ МОДЕЛИРОВАНИЯ

В ИНТЕГРАЛЬНОЙ ПОСТАНОВКЕ

Такие задачи заключаются в определении индивидуализированных режимов ГМ, обеспечивающих адекватность ИСТ и ЕСТ. Под этим понимаются два состояния объектов ГМ: либо

ТрубППр™Д с тпкисп.ю

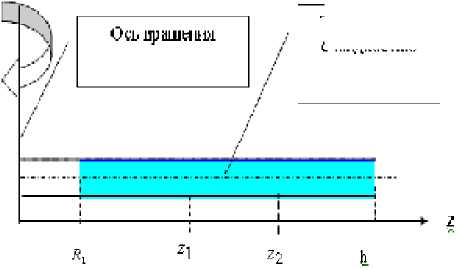
Рис. 3. Схема обозначений, принятых в (1) – (4)

соответствие ИСТ и ЕСТ (энергетический баланс: δ = 0, см. поз. 3.2.1, рис. 2), либо заданные уровни рассогласований ( δ < 0 или δ > 0, см. поз. 3.2.2). Моделирование выполняется по формуле (43), которая получена разрешением (2) относительно ω , что и определило название задач – “обратные”.

to = ± 5,425 ( h - R1) Hi h ³

в (1 + 0,0М)

- R ²(3 h - 2 R 1 )

• (3)

Отметим следующие наиболее важные моменты. Во-первых , модель (3) устраняет неопределенность “точечного” подхода к оценке адекватности ГМ в случае ПО. Она однозначно определяет режимы испытаний, обеспечивающие разнообразие требований, предъявляемых к ГМ, осуществляющему моделирование ЕСТ. В их числе: множество объектов, отличающихся габаритами и расположением на столе ЦКР; множество их состояний ( δ ); многообразие планет

( β ); промежуточные варианты β . Во-вторых , для получения оптимального режима, которому соответствует минимум отличий из числа возможных, достаточно в (3) положить δ = 0. В-третьих , для получения заданного рассогласования ИСТ и ЕСТ, что важно с научно-практической точки зрения, достаточно в (3) положить соответствующее значение δ с учетом величины и знака. С целью удобства применения (3) в АИСОА предусмотрен отдельный типовой экран, который, как и в случае прямых задач, обеспечивает массовость прогонов.

ПРЯМЫЕ И ОБРАТНЫЕ ЗАДАЧИ ГМ В ЛОКАЛЬНОЙ ПОСТАНОВКЕ

В целом ряде приложений необходима оценка адекватности ИСТ и ЕСТ на локальном участке гидравлической системы (см. рис. 3, интервал [ Z i ,z 2 ], где R 1 <  z_x <  z ₂ <  h ). Как следствие различий в законах распределения гидростатического давления (линейность) и инерционного давления (семейство парабол, смещенных относительно начала координат), взаимное расположение эпюр распределения давления отличается и количественным, и качественным разнообразием. Создается множество состояний объектов, когда интегральная оценка, а она усредняет энергию жидкости на интервале [ R 1 , h ], не совпадает с локальной оценкой. Опуская преобразования (интегрирование законов распределения давления на интервале [ Z 1 , Z ₂] ),

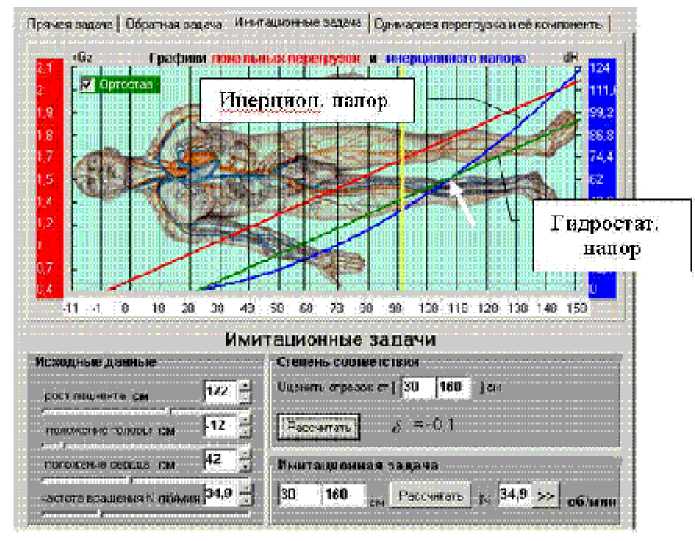
Рис. 4. Типовой экран АИСОА для решения прямых задач в интегральной и локальной постановке

приведем конечную формулу для оценки адекватности в локальной постановке:

22     2  2

^ = (-^_ z2 + z2 z1 + z1 - 3 ^ -1) .100%.(4) 3g g в    z2 + Z1 — 2^T              ( )

Отметим, что модель (4) является аналогом (2). Она реализована в блоке 3.1.1 АИС (см. рис. 2) и для удобства пользователя решается на том же экране, что и интегральная задача (см. рис. 4).

С точки зрения ГМ особый интерес представляет задача, получившая наименование “обратной задачи в локальной постановке”. Для ее решения достаточно определить to из соотношения (4):

® лок =± 5,425

в ( z 2 + z 1 - 2 ^ 1 )(0,01 ^ _ЛОк + 1) z 2 + Z 1 z 2 + Z 1 — 3 ^ 1

Учитывая логическое сходство обратных задач (3) и (5) для их решения отведен один и тот же экран интерфейса пользователя.

ИНФОРМАЦИОННАЯ ПОДДЕРЖКА ПРИНЯТИЯ РЕШЕНИЙ

Рассматриваемый комплекс задач обладает особой актуальностью в ГМ с непосредственным участием человека в сеансах вращения как в условиях Земли, так и Космоса [2, 4, 6]. Результаты моделирования, а они включают в себя как перечисленные, так и некоторые другие данные, в частности эпюры распределения гидростатического и инерционного давления, распределения перегрузок (см. график на рис. 4), поступают в блок 4 АИСОА (рис. 2). На основании полученной информации ответственные исполнители ГМ принимают решение либо о проведении испытаний, которое по обратной связи (ОС1) передается на уровень физического моделирования (поз. 2), либо выполняют кор- рекцию исходных данных с повторным моделированием (ОС2 или ОС3).

В заключение отметим, что апробация предлагаемой АИСОА на реальной информации, предоставленной Институтом медико-биологических проблем РАН, а он является одним из мировых лидеров по обеспечению пилотируемой космонавтики [2-4], показала ее высокую эффективность, научную новизну и практическую значимость.