ГИГАНТСКАЯ ДИСПЕРСИЯ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ДИСПЕРСНОЙ СИСТЕМЫ В ПЕРЕМЕННОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ. ОБЗОР ПОДХОДОВ, УЧИТЫВАЮЩИХ НАЛИЧИЕ ДВОЙНОГО СЛОЯ

В работе [1] в интересах увеличения скорости электрофореза дисперсной фазы была рассмотрена возможность использования эффекта большой низкочастотной дисперсии относительной диэлектрической проницаемости в дисперсной системе, состоящей из дисперсной фазы в виде шарообразных частиц с параметрами ε ₂ , σ ₂ , помещенных в однородную дисперсионную жидкость с параметрами ε ₁, σ ₁, ( ε_i и σ_i ( i = 1, 2) — относительные диэлектрические проницаемости и удельные проводимости соответствующих сред) в условиях поляризации Максвелла – Вагнера (ПМВ) [2, 3]. ПМВ носит название макроскопической, т.к. в ней игнорируется наличие двойного слоя на границах раздела фаз и не учитывается тем самым диффузный характер распределения заряда на границах раздела, что ведет к ограниченности применения этой теории областью тонкого двойного слоя к а » 1, где к = 1/ X D , a — радиус включения, 2 D — радиус экранирования Дебая. В настоящей работе приводится обзор двух моделей теории поляризации дисперсных систем в условиях развитого диффузного распределения заряда двойного слоя: теории микроскопической поляризации Трухана [4–6] и Духина – Шилова [7].

Вначале выпишем наиболее полную систему уравнений, описывающих процесс поляризации в общем виде [7, § 3.1, § 3.2]:

∂v

ρ   = -∇p+η∆v+ ρeE0,(1)

∂ t

∇⋅v=0,(2)

∇j± + ∂c± =0,(3)

∂ t

Δϕ= - 4πρel (в СГСЭ).(4)

ε

Система уравнений, описывающая рассматриваемый процесс, состоит из гидродинамического блока, включающего модернизированное уравнение Навье – Стокса для малых чисел Рейнольдса (1) (называемое в этом случае уравнением Стокса) и уравнение непрерывности для несжимаемой жидкости (2). Уравнение (3) является уравнением непрерывности потока ионов (см., например, [7, с. 76]). В качестве вектора j ^± рассматривается плотность потока этих ионов [7, с. 76]:

j ^± = c ^± v _migr - D ^±∇⋅ c ^±+ c ^± v =

= ± c ^± µ ^± E - D ^±∇ ⋅ c ^± + c ^± v .          (5)

Наконец уравнение Пуассона (4) описывает поведение электрического потенциала ф ( -V ф = E ; описание вектора E см. ниже) при наличии распределения плотности электрического заряда ρ _e .

В уравнениях (1)–(4), кроме отмеченных, приняты следующие обозначения: р = const — плотность несжимаемой жидкости; v — вектор поля скорости жидкости; p — поле давления в жидкости; η — динамическая вязкость жидкости; вектор электрической напряженности внешнего поля E ₀ ориентирован, например, по оси Oz Е о = (0,0, E_z ) и имеет гармонический характер E ₀ = k E z e-' ^{m t} , где k — орт вдоль оси Oz; £ — относительная диэлектрическая проницаемость; D — коэффициент диффузии иона; c — коэффициент концентрации; µ — подвижность иона. В работах [4–7] функция источника ρ _e E ₀ в уравнении (1) отсутствует, взамен этого ставится граничное условие о том, что значение электрического поля в системе E на бесконечности стремится к значению E ₀: E ₀ = lim E , x — вектор текущей

I х| ^х точки в исследуемой области; именно значение поля E фигурирует в (5). Обусловлено это тем, что в среде присутствует также поляризованное электрическое поле, обусловленное потенциалом ϕ из (4). Согласно [6, с. 8], поле E имеет вид:

E ( x , t ) = E ( x ) e “ , ф ( х , t ) = ф ( x ) e “ ,                  (6)

E (x) = -V ф( x).

Далее переходим к конкретному рассмотрению заявленных видов поляризации.

щей среде . Задача рассматривалась в предположении, что период колебаний T = 2 л/® , среднее столкновительное время релаксации подвижных носителей τ ₁ и среднее время рекомбинации зарядов противоположного знака в проводящей фазе т ₂ связаны соотношением т 1 >  T >  т ₂; это ограничивает область рассмотрения частот диапазоном частот f = “ (2 п ): 10 3 -10⁶<  f < 10^п-10¹² Гц [6, с. 8]. Для взвеси проводящих сфер в изоляторе точное выражение для комплексной совокупной диэлектрической проницаемости ε ^* получается на основе соотношения £ = D / E , где D и E — средние комплексные амплитуды электрической индукции и напряженности поля соответственно. Взаимодействием системы сфер пренебрегается, т.е. принимается, что величина удельного объема а шаровых включений а = (4/3) па ³ N ( a — радиус шаровых включений; N — число включений в единице объема или их концентрация) мала: а ^ 1.

Изначально принимается условие малости числа Пекле Pe = a^ ^ 1 (здесь V — характерный размер скорости; a — характерный размер дисперсной частицы), что позволяет опустить конвекционный член c ± v в (5) и свести систему (1)-(5) к двум несвязанным системам: гидродинамической (1), (2) и электрохимической (3)–(5).

Здесь приведем решение задачи (3) в предположении, что D += D~= D и |^ +|= |^"| = ^. Концентрация ищется в виде c 4x, t ) = (c о + Y ±( x))e - “t при условии слабой поляризации

Y ± <  c 0 .

Здесь c ₀ — равновесная концентрация ионов (дисперсных частиц); y ± — амплитуда отклонения концентраций от равновесного значения, которая полагается много меньшей равновесной концентрации.

Предположение (7), (8) позволяет линеаризовать задачу и получить для плотности заряда уравнение

A P e ( ^x ) = X ² P e ( x ) ,                   ⁽⁹⁾

где

X ² = к ² + i “ ,       к = 1/ A d .             (10)

С учетом условия конечности плотности заряда в центре сферы решение (9) имеет вид

Pe ( r ) =

A cos 9 x sh (r)) ------- ch (r)-- r к          r J

с т = ас ₂

1 5 ' t , к ^£ 2 J

ωε t = —2-

σ ₂

где r = |x| отсчитывается от центра сферы. После подстановки (11) в уравнение Пуассона автор теории поляризации получает уравнение для определения потенциала ϕ , которое существенно отличается от уравнения (9). Далее автор находит распределение потенциала ϕ в окрестностях сферы. На основании этого им получается выражение для дипольного момента d _e ^* (дипольный момент позволяет представить дипольную составляющую ϕ _D электрического потенциала ϕ сферы во внешней области ^ D = d * cos 9/r ² ) [6, с. 11]:

и монотонно растет с частотой и достигает предельного значения с „

с „ = 9ас 2

ε ₁

к ^£ 2 J

d * =

π

1 —+ в

ε ₂

2 (

1 + ^£

—

ε ₁ a ³ E ₀,

к

ε ₂

1 + 2 f t .

к      ^£ 2 J

Физический смысл расхождения данной теории с теорией поляризации ПМВ заключается в том, что в теории ПМВ пренебрегается наличием диффузного заряда на границе раздела фаз, т.е. заряд полагается чисто поверхностным. Это справедливо только при условии K a ^ 1. В общем случае считать заряд поверхностным (ПМВ) неверно. В работах Я.И. Френкеля [8] и Э.М. Трухана [4 и др.] произведено обобщение теории ПМВ на случай произвольного соотношения между величиной дебаевского радиуса экранирования и размерами включений.

где в =

_£K 2 ( 3 + ( Xa ) 2 ) th ( Xa ) — 3xa

^{£ 2 X} [ 2 + ( Xa ) 2 th ( Xa ) — 2 Xa ]

Для системы сферических включений при их удельном объеме a ^ 1 получено следующее выражение для результирующей диэлектрической проницаемости гетерогенной системы:

*      [ 1 + 3 a ( 1 — £j £ 2 + в ) ]

£ = £ ----------------------,

¹     1 + 2 £ 1 / £ ₂ — 2 в

где β определяется из (13). Характер частотной зависимости £ = Re (£ ) похож на соответствую- щую зависимость теории поляризации ПМВ.

Диэлектрические свойства такой системы характеризуются удельным инкрементом δ

5 = £—= £ /£1 1 = 5'— i5", ε1α      α который, как видно из формулы, равен изменению диэлектрической проницаемости дисперсионной среды за счет присутствия дисперсной фазы на единицу удельного объема и на единицу исходной диэлектрической проницаемости дисперсионной среды.

Удельная проводимость среды σ при одинаковых подвижностях ц + = ц _— = ц равна

ПОЛЯРИЗАЦИЯ ДУХИНА – ШИЛОВА

Авторами теории, в отличие от модели, рассмотренной выше, была исследована система различных непроводящих включений в проводящей среде . Важным свойством границы раздела включений и дисперсионной жидкости, влияющим на поляризацию дисперсных систем и не учтенным ни в теории ПМВ, ни в работах [4] и [8], является заряженность поверхности раздела. Заряд на поверхности раздела обуславливает наличие двойного слоя и связанной с ним дополнительной поверхностной проводимости, которая влияет на распределение потенциала, возникающего во внешнем электрическом поле [7, с. 7]. Исследование влияния диффузионного механизма на поляризацию в предельном случае K a » 1 привело авторов к выводу о низкочастотном отставании поля поляризации от внешнего электрического поля, что и является причиной наблюдаемых на опыте гигантских значений низкочастотной диэлектрической проницаемости дисперсных систем [7, с. 8]. В то же время область рассмотрения теории поляризации Трухана начинается с частоты f >  10 3 Гц (см. выше).

В [7, с. 42] приводится факт того, что наличие удельной поверхностной проводимости λ в области двойного слоя так же влияет на поляризационные поля сферических частиц радиусом a, как и увеличение их объемной проводимости σ на величину 2λ a, т.е. результирующая объемная проводимость <г при наличии поверхностной про- водимости равна о = о + 2^a. В переменном поле возникает дисперсия поверхностной проводимости из-за того, что больцмановское равновесие в двойном слое уже не успевает восстанавливаться, что и приводит к дисперсии поверхностной проводимости. Отмечается также [7, с. 43], что наличие у частицы дисперсной фазы большого постоянного дипольного момента также скажется на диэлектрических свойствах суспензий и растворов макромолекул.

Большие размеры дисперсных частиц по сравнению с молекулами полярного растворителя обуславливают дисперсию диэлектрической проницаемости на низких частотах [7, с. 46]:

^S = ^S h ^{+ ( S} 0 ^S h )    / х 2 ,

1 + (тю)

3ηVpNA где т = —время релаксации; Vp — объем частицы; NA — число Авогадро. Там же приведено выражение для дисперсии диэлектрической проницаемости и для частиц несферической формы. В этом случае диэлектрическая проницаемость характеризуется набором времен релаксации [7, с. 46]. Далее в [7, с. 51] приводится очень важное замечание о том, что в дисперсных системах с проводящей дисперсионной средой возможен механизм усиления влияния поляризации на действительную часть диэлектрической прони-цаемости1). Этот механизм объясняется в [7] следующим образом. При подаче переменного поля к дисперсной среде возникает процесс поляризации, который отстает от исходного электрического поля, что приводит к отставанию тока проводимости, вызванного поляризационным электрическим полем. Этот ток в силу его отставания от внешнего поля интерпретируется как ток смещения. Наличие же значительных токов смещения в среде на низких частотах воспринимается экспериментально как высокая диэлектрическая проницаемость среды (см., например, выражение (1.54) работы [7] для диэлектрической проницаемости ε* неиде-*     4πσ ального конденсатора: s = s +----, где S — ди- iω электрическая проницаемость диэлектрика в конденсаторе, σ — его удельная проводимость).

Далее в [7, с. 52, 53] приводится важное условие появления высоких значений диэлектрической проницаемости суспензий, связанных с поляризацией двойного слоя частиц:

ка > 1.

Наряду с этим условием для возникновения гигантской низкочастотной дисперсии необходимы немалые значения величин поверхностного заряда . Далее авторы отмечают, что только при условии к а ^ 1 действует проанализированный эффект гигантского усиления диэлектрических явлений [7, с. 55].

Рассмотренный в [7] механизм гигантского усиления влияния поляризации включений на диэлектрическую проницаемость дисперсной системы, по мнению авторов работы, должен иметь место для более широкого класса систем, чем суспензии и электролиты, для которых построена соответствующая теория в [7]. Здесь, видимо, уместно повторить, что речь идет действительно о гигантских значениях диэлектрической проницаемости, которая, например, в водных суспензиях достигает размеров порядка ε ~ 10⁴. Такая низкочастотная дисперсия диэлектрической проницаемости наблюдалась для проводящих суспензий и растворов полиэлектролитов [7, с. 55].

Характерные признаки дисперсии диэлектрической проницаемости

– Очень высокие значения низкочастотного предела, достигающие 105.

– Большая величина времени релаксации, квадратичная зависимость времени релаксации от линейных размеров частиц. Оценка времени релаксации может быть сделана по формуле

τ ~ l ²/ D ;

где l — характерный размер частицы (макроиона); D — коэффициент его диффузии в растворе электролита.

– Повышенная проводимость противоионов двойного слоя.

Согласно [7, с. 56], обнаружена также зависимость низкочастотной диэлектрической проницаемости от величины pH.

Учет перечисленных условий позволяет объяснить высокие значения диэлектрической проницаемости на основе существующих представлений о строении диффузной части двойного слоя.

При разработке рассматриваемой теории за основу также берется система уравнений (1)–(5). Распределение потенциала U и концентрации c ± в дисперсной среде ищется в виде [7, с. 63]

Ф = Ф о +Ф о + U 1 , c "= c ± + Y 0 ± + Ct . (17)

Здесь Фо — равновесное распределение электрического потенциала в двойном слое частицы в отсутствие внешнего электрического поля; ϕ0 — распределение электрического потенциала под воздействием внешнего поля; U1 — линейная по внешнему полю поляризационная добавка (принимается предположение о достаточно малой величине внешнего поля для справедливости достаточности только добавки U1); с± — поляризационное распределение концентрации; с± — концентрации ионов в свободном электролите; у± — отклонение концентраций с ± в окрестностях двойного слоя; с± — линейные по внешнему полю поляризационные добавки к концентрациям.

Стационарная поляризация

Далее авторами рассматривается двойной слой сферической частицы в постоянном электрическом поле [7, § 3.1] (в этом случае уравнение непрерывности (3) сводится к стационарному случаю V j ± = 0). При этом принимается допущение о приближении тонкого двойного слоя (16), что позволяет рассматривать его как локально плоский. Поляризационный потенциал и концентрации ищутся в виде

U 1 = ф +Ф„ Cf = с⁺_? + Y, .

В результате непростых выкладок в [7] получены следующие результаты.

– Распределение Больцмана сохраняется для концентрации ионов и для поляризованного тонкого двойного слоя с тем отличием, что к обычному распределению Больцмана распределения концентрации ионов добавляется зависящий от полярного угла θ предэкспоненциальный множитель ( 9 = 0 соответствует направлению постоянного электрического поля), т.к. концентрация ионов изменяется вдоль внешней границы двойного слоя [7, с. 70], и, следовательно, структура поляризованного двойного слоя совпадает со структурой равновесного двойного слоя (в отсутствие внешнего электрического поля).

– Напряженность поля, возникающая внутри двойного слоя при его поляризации, в κ a раз превышает напряженность поля у его внешней границы; в подобной ситуации выполнение условий непрерывности потоков ионов внутри двойного слоя возможно лишь за счет почти полной компенсации нормальных компонент электромиграционных и диффузионных потоков ионов, что и приводит к необходимости выполнения распределения Больцмана [7, с. 75].

– При слабой поляризации двойного слоя (т.е. при выполнении условий с ± » y С ± из (17))

автоматически следует выполнение условия мало-Va сти критерия Пекле Pe = — ^ 1 (см. выше), что позволяет свести систему (1)–(5) к двум несвязанным системам: гидродинамической (1), (2) и электрохимической (3)–(5) [7, с. 76].

Поляризация в переменном электрическом поле

Далее авторы обобщают полученную для стационарного режима теорию на случай переменных полей не слишком высокой частоты, сохраняя при этом упрощающие факторы, учтенные в теории стационарной поляризации. За основу вновь берется система уравнений (1)–(5), однако с уравнением непрерывности в неусеченном виде (3). При этом вновь принимается допущение относительно малого перепада концентрации, ведущего к малости числа Пекле и, следовательно, к независимости уравнений (1), (2) и (3), (4).

Далее авторы находят ограничение по частоте внешнего электрического поля (выражение (III.88) [7, с. 77]), при котором сохраняется локальное равновесие в двойном слое и при поляризации в переменном электрическом поле для концентраций ионов можно использовать в двойном слое распределение Больцмана [7, с. 78] (квазистацио-нарное решение). Вследствие малых чисел Пекле рассматриваемой задачи авторы заменяют условие приближенной локальной электронейтральности за пределами двойного слоя условием полной электронейтральности. На этом основании вводится функция с = с⁺/z = с~/z ⁺ , для которой справедлив анзац [7, с. 77]

с = с 0 + с, (r ,9) e ',(18)

а для потенциала вне частиц:

Ф = ф( r ,9) e-i'.(19)

Условие квазистационарности выполняется при выполнении условия [7, с. 78]:

2π1

T = — > —2-, или to^2nvK2,(20)

ω  νκ ²

где ν — кинематическая вязкость дисперсионной среды.

Решение для ϕ и c ищется в виде с = с0 + dccr (r) cos 9e '™t,                (21)

I d "-D+

Ф = <  ф + d_c ——------с_г ( r ) cos 9 +

I ^с z ⁺ D ⁺+ z ^- D ^- r^v ’

d

+cos9> e"™‘, r I ф0 =-

'E f r +1 aT^ cos 9, I 2 r )

где E — амплитуда гармонического электрического поля E = |E| ; d c , d _v и c r определены в [7, с. 80].

После подстановки d _ϕ в формулу (II.39) работы [7, с. 52] с точностью до величины ( Ka ) ² получается следующее выражение для невязки между диэлектрическими проницаемостями поляризованной дисперсной смеси и дисперсионной жидкости (т.е. диэлектрического инкремента A s = s* - £ 1 ) [7, с. 81]:

As =

9    , v ( Ai a 2 — A 2 а1 )(1 + W + W 2)

= ае 1 ( ка ) ----------------------------- 2_ _. _   (24)

⁴          ( A 1 + AW ) ² + ( A 1 W + A ₂ W ² )

Величина статического диэлектрического инкремента As st = lim As равна² ) [7, с. 81] го ^ 0

9         2 A,a ₂ - Aa,

^{A s} st = 4 ^as i ( ^{K a} ) — 2—T^{1 L}-             ( ²⁵ )

рассматриваемой дисперсной среды ( s" = Im ( s*

определяется выражением [7, с. 83]

s = —as 1 ( Ka ) x

( A , a ₂ — A ₂ a , ) ( AW + A ₂ W ² ) 2 A , ( A , + A 1 W ) 2 + ( A 1 W + A ₂ W² ) 2

Из (27) видно, что величина ε '' мала на очень низких частотах при W «^ 1 и на высоких частотах при W ^ 1, достигая максимального значения при W ~ 1, при этом, согласно зависимости (27), частота, на которой достигается максимум диэлектрических потерь, т.е. при s " ^ max будет обратно пропорциональна квадрату радиуса частицы a ² .

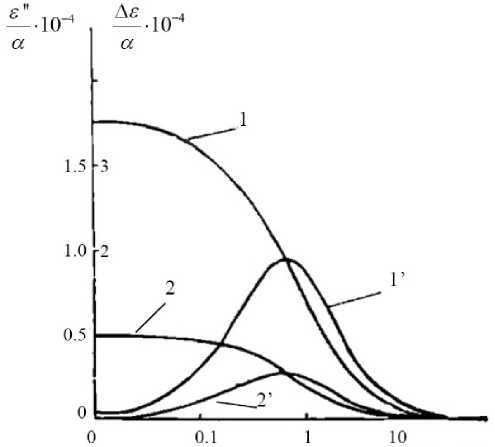
На рисунке приведена зависимость величины удельного инкремента реальной части диэлектри- ческой проницаемости As /a от величины W ,

Здесь величины A ₁ , A ₂ , a ₁ и a ₂ определены в [7, с. 80], W = a/r ₀ , где r₀ = ^2 D e / го — характеризует толщину диффузного слоя при частоте ω ; + 7-4— +       ~        + 7-4+      — 7-4—

e = D D (z + z )/(z D + z D ) [7, с 77].

Далее понадобится зависимость a a a2ω

W =  = 1     =-/—.

r 0     2 D e / ω 2 D e

На частотах, когда W ~ 1, поляризация частицы существенно отстает по фазе от приложенного поля и действительная часть дипольного (поляризационного) момента изменяется наиболее быстро. Таким образом, медленный процесс установления распределения концентраций за пределами двойного слоя приводит к существенному отставанию поляризации частицы от внешнего

D поля на частотах ω~ 2e . На этих частотах возни-a2

кают высокие значения при малой толщине двойного слоя, когда K a » 1 [7, с. 81].

Для симметричного электролита с точностью до величины ( Ka ) ² величина мнимой части s" комплексной диэлектрической проницаемости ε ^*

Log w

[7, рис. 11]: зависимость инкремента реальной части диэлектрической проницаемости A s / a (1, 2) и удельной величины мнимой части диэлектрической проницаемости ε ''/ α (1’, 2’) от логарифма величины W для водных суспензий сфер при Ka = 50. Кривые 1 и 1’ получены при значении ζ-потенциала в полтора раза большем, чем в случае кривых 2 и 2’

а фактически от ω в логарифмическом масштабе, по оси абсцисс (величина α — по-прежнему величина удельного объема шаровых включений в дисперсионной жидкости). Заимствован рисунок 11 работы [7, с. 81]. Одновременно на рисунке приведены зависимости величины ε ''/ α . Из рисунка виден характер поведения величин Δ ε / α и ε ''/ α , а также прямая зависимость этих величин от величины ζ-потенциала.

ВЫВОДЫ

В результате проведенного обзора следует вывод о том, что при выполнении условия наличия тонкого двойного слоя вокруг непроводящих дисперсных частиц в проводящей дисперсионной среде возникает возможность появления гигантской дисперсии действительной составляющей диэлектрической проницаемости, которая может существенно изменить скорость электрофореза таких частиц.

Работа выполнена в ИАП РАН в рамках Государственного задания 075-00780-20-00 по теме № 0074-20190013 Министерства науки и высшего образования.