Гиперболическая секансная линза со щелью для субволновой фокусировки света

Оптические микролинзы играют важную роль в миниатюризации современных устройств нанофотоники. Они часто используются в лазерных излучателях, приёмниках оптических сигналов, в микроскопии, сопряжении волноводов и т. д. Достижение сверхразрешения в устройствах нанофотоники помогает ещё более уменьшить размеры оптических устройств, достичь новых возможностей как в обработке, так и в передаче информации. При этом важны как достижимая острота фокусировки излучения, так и её энергетическая эффективность. Например, в [1–3] при моделировании было получено фокусное пятно с диаметром λ/2– λ/4. В [1, 2] для острой фокусировки света использовали дифракционную линзу с относительно большим фокусным расстоянием, в связи с чем диаметр фокусного пятна по полуспаду интенсивности (FWHM) был равен λ/2. Для увеличения числовой апертуры и уменьшения фокусного пятна широко применяют иммерсионные линзы [3]. С помощью них авторы в [3] достигли ширины фокусного пятна FWHM = λ/4 при показателе преломления линзы n =2 и числовой апертуре NA= 1,7. А при использовании метаматериалов и иммерсионной оптики [4] возможно достичь эффективной числовой апертуры NA=4,5 и фокусного пятна с диаметром FWHM= λ/9 при фокусировке света в материале линзы. Однако такое узкое фокусное пятно остаётся внутри линзы. Уменьшению фокусного пятна способствует фокусировка радиально или азимутально поляризованного света [5, 6]. Например, в [6] получена фокусировка света в фокусное пятно FWHM = λ/3 в воздухе. Одним из способов преодоления дифракционного предела является фокусировка света с помощью плазмонов на периодических структурах [7, 8]. Таким образом можно получить острую фокусировку света, периодически повторяющуюся в пространстве. Широко используются для фокусировки света нанощели [9, 10]. Например, в [9] получена локализация в пятно шириной около λ/2 света, выходящего из «субволнового генератора» – двух щелей шириной 80 нм каждая. А в [10] рассматриваются линзы, состоящие из щелей нанометрового размера в золоте. Свет, проходя через щели шириной 20 нм, фокусируется в область около половины длины волны. Числовая апертура щелевой линзы составляет при этом NA=0,75. В [11] рассмотрена локализация в метаматериале света, выходящего из двух и более щелей. Свет, выходящий из щелей в экране шириной 20 нм, интерферирует в метаматериале, состоящем из плёнок Ag и SiC, и на границах расходящихся световых потоков от каждой щели образуется световое пятно шириной FWHM=22 нм, или λ/17. Эффективность такой локализации света авторы не указывают, предположительно, она должна быть невелика, так как только края световых потоков участвуют в формировании узкого светового пятна. Также не указано, как можно вывести такое острое фокусное пятно из метаматериала. Интересно, что щель, ширина которой имеет порядок десятков нанометров, может служить для локализации и распространения в ней света, как в волноводе [12, 13]. Широко распространены градиентные линзы для острой фокусировки света, в частности, планарные фотонно-кристаллические линзы [14, 15]. В [16] фокусировка в область приблизительно λ/4 осуществляется массивом отверстий в тейпере, что позволяет сопрягать два планарных волновода. В [17, 18] рассматривается дифракция света на нанощели в метаматериалах. Располагая планарную гиперболическую линзу из многослойного метаматериала за экраном со щелью, можно добиться субволновой фокусировки света в такой линзе. В [17] получена фокусировка света в пятно FWHM = λ/10, в [18] при подобной оптической схеме – λ/5. В этих работах линза состоит из десятков слоёв серебра толщиной 5 нм и SiC толщиной 10 нм. Изготовление её на практике затруднительно.

Данная работа суммирует полезные качества щели шириной несколько десятков нанометров для локализации света и градиентной линзы для острой фокусировки света, например, линзы Микаэляна [19, 20]. Рассмотрена острая фокусировка света с помощью планарной градиентной линзы в двумерном случае с использованием щели для локализации света в узком пятне, шириной FWHM близким к ширине щели. Например, для планарной бинарной микролинзы в кремнии со щелью шириной 50 нм с энергетической эффективностью 44% формируется вблизи поверхности линзы фокусное пятно с шириной FWHM = λ/23. Это меньше, чем сообщалось во всех перечисленных выше работах [1 – 18]. Фокусировка производится на границе линзы, таким образом, острое фокусное световое пятно доступно для различных приложений нанофотоники. Отметим, что в работах

[4, 6, 7, 9– 11, 13– 15, 17–20] тоже рассматривался двумерный расчёт фокусировки света. Расчёт света градиентной линзой со щелью в двумерном случае позволяет получить качественную оценку фокусировки света. В трёхмерном случае результаты по эффективности и ширине фокусного пятна могут отличаться приблизительно на 30%, что показано в [19].

Моделирование

Схема рассматриваемой задачи представлена на рис. 1.

Планарный              Планарная градиентная

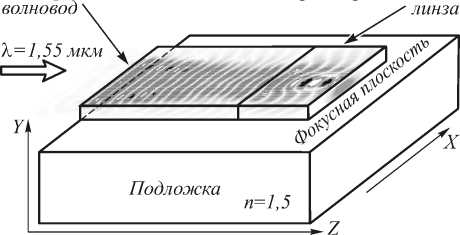
Рис. 1. Схема рассматриваемой задачи

Свет, выходящий из планарного волновода, выполненного из кремния ( n 0 = 3,47) на подложке из плавленого кварца, фокусируется градиентной линзой. Максимальный показатель преломления градиентной линзы на оптической оси равен показателю преломления в волноводе n 0 .

На рис. 2 представлена схема планарной градиентной линзы со щелью. В качестве градиентной линзы рассмотрим планарную гиперболическую се-кансную (ГС) линзу, показатель преломления которой зависит от поперечной координаты x следующим образом [19, 20]:

n ( x ) = n 0

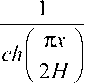
где H – длина линзы.

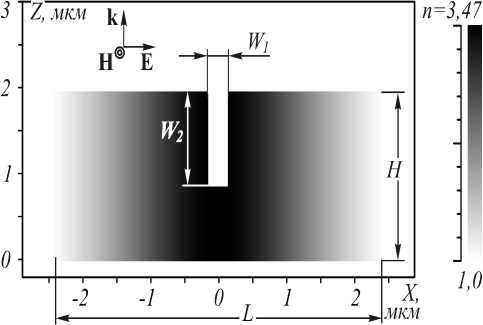
Рис. 2. Распределение показателя преломления (в полутонах) градиентной линзы со щелью, направления векторов электрического и магнитного полей показаны для случая ТМ-поляризации

Щель в планарной ГС линзе шириной W1 располагается на оптической оси линзы и доходит до выходной фокусной плоскости линзы. Щель может проходить через всю линзу (W2= H) или находиться в последней части линзы (W2< H). Ширина щели W1 может быть менее дифракционного предела фокусировки света в материале линзы на оптической оси.

Моделирование распространения света через линзу проводилось методом FDTD, реализованным в коммерческом программном обеспечении FullWave (фирма RSoft). На рис. 3 представлен график распределения интенсивности в фокусной плоскости линзы без щели, на расстоянии 10 нм за выходной плоскостью линзы. Параметры моделирования: H = 1,95 мкм, L =4,8 мкм, показатель преломления на оптической оси n = 3,47 (кремний), длина волны света λ = 1,55 мкм, падающая волна плоская, ТЕ-поляризация. Длина линзы H подобрана для оптимального фокусного пятна. Отметим, что в случае ТМ-поляризации качество фокусирования света градиентной линзой без щели будет намного хуже (фокусное пятно будет шире в 4 раза, а боковые лепестки близ фокуса будут составлять приблизительно половину от фокусного пятна).

I,

1,

• 1,

О, отн. ед.

• -1,0        -0,5         0          0,5        1,0

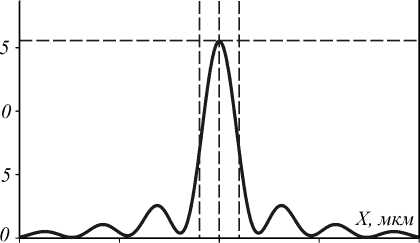
Рис. 3. Распределение интенсивности излучения в фокусе линзы |Ey|2 при отсутствии щели, падающая волна имеет ТЕ-поляризацию

На рис. 3 ширина фокусного пятна по полуспаду интенсивности FWHM = 0,181 мкм = 0,117λ. Это значение меньше дифракционного предела в среде, который составляет для данного показателя преломления FWHM = 0,44( 1 /3,47) = 0,127 1 . Покажем, что, используя щель на оптической оси линзы с показателем преломления в щели n = 1 и начальное световое поле с ТМ-поляризацией, можно достичь более острой фокусировки света. На рис. 4 а приведён график зависимости ширины фокусного пятна FWHM от ширины щели W 1 . Длина щели была взята равной длине линзы W 2 = H =2,2 мкм, остальные параметры моделирования такие же, что и для рис. 3.

Из рис. 4 а видно, что ширина фокусного пятна по полуспаду интенсивности линейно зависит от ширины щели в линзе W ₁, фокусное пятно немного шире её. На рис. 4 б привёден график зависимости интенсивности в фокусе линзы при W 1 =50 нм. Видно, что интенсивность света в фокусе линзы со щелью примерно в 6,5 раз больше, чем в случае линзы без щели (рис. 3) при прочих равных параметрах.

Дифракционная эффективность фокусировки света ηD планарной градиентной линзой со щелью в область, близкую к ширине щели, также зависит от ширины щели W1. Максимум эффективности фокусирования света наблюдается при W1 ≈ 40 нм, при увеличении ширины щели наблюдается спад эффективности ηD (рис. 5а). Такой эффект обуславливается, во-первых, уменьшением интенсивности света в фокусе при увеличении ширины щели W1 (рис. 5б), а во-вторых, изменением боковых лепестков и, как следствие, изменением ηD. Эффективность ηD рассчитывалась как отношение энергии, заключённой в центральном лепестке картины дифракции в фокусе (приблизительно –75 нм < X <75 нм на рис. 4б), ко всей энергии, пришедшей в выходную плоскость шириной L.

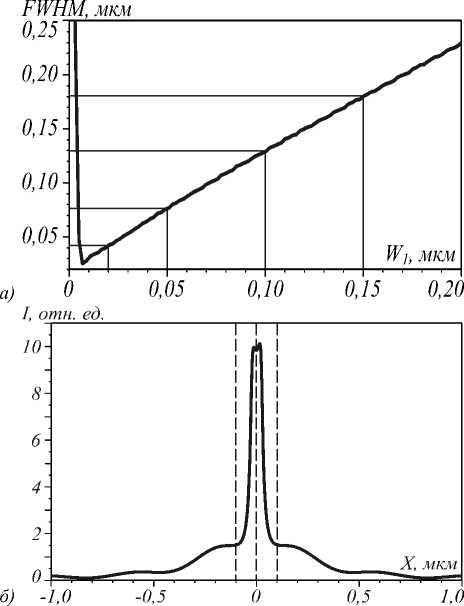
Рис. 4. Зависимость ширины фокусного пятна по полуспаду интенсивности от ширины щели W1 (а), распределение интенсивности I = |Ex|2 + |Ez|2 в фокусной плоскости (10 нм от линзы) при W1 = 50 нм (б)

Из рис. 4 а также видно, что при ширине щели W ₁<5 нм ширина фокуса начинает расти. При этом минимальная ширина фокусного пятна достигается при W 1 =5 нм и равна FWHM = 13 нм = λ/119. Для сравнения на рис. 3 фокусное пятно имеет ширину FWHM = λ/8 и эффективность η D = 60%.

Из рис. 5 видно, что при рассматриваемых параметрах максимальная эффективность равна η D =39,9%, а ширина фокусного пятна при этом равна FWHM=55 нм = λ/28 (см. рис. 4 б ).

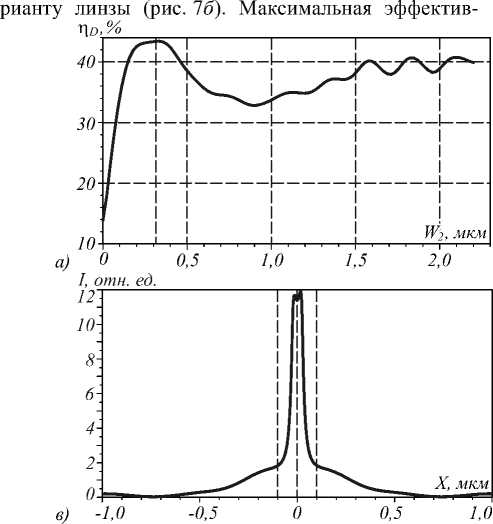
На рис. 6 показаны зависимости эффективности фокусировки света ηD (6а) и интенсивности света в фокусе линзы (6б) от длины щели W2 для фиксированной ширины щели W1 =50 нм. Для расчёта эффективности ηD здесь так же, как и для рис. 5, учитывалась область наиболее острой части фокусного пятна (до ближайших боковых лепестков) и была взята –75 нм < X <75 нм. Из рис. 6 видно, что в отсутствие щели (W1 = W2=0) дифракционная эффективность фокусирования света около 10%.

Видно, что максимальные значения эффективности фокусировки η D и интенсивности светового поля возникают при длине щели, обеспечивающей задержку фазы на λ/2, что при рассматриваемой длине волны и показателе преломления соответствует W 2 = λ / (2( n 0 – 1)) = 0,314 мкм. Эффективность фокусировки света в этом случае достигает η D = 43,4%. При этом интенсивность света в фокусе линзы больше приблизительно на 20% (рис. 6 в ), а боковые лепестки менее выражены, чем в случае W 2 = H (рис. 4 б ). Из рис. 6 г видно, что наибольших значений интенсивность светового поля достигает приблизительно на расстоянии 30 нм от края линзы внутри щели.

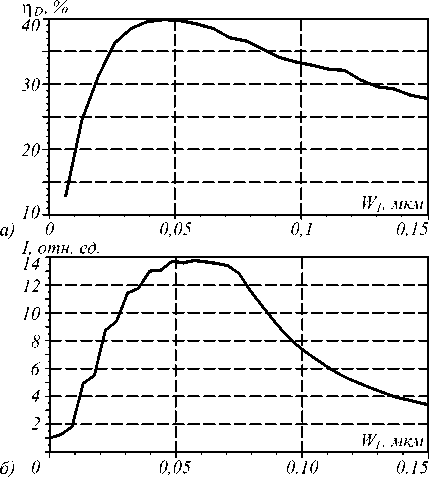
Рис. 5. Зависимость эффективности фокусировки света ηD (а) и интенсивности в произвольных единицах в фокусе линзы (б) от ширины щели W1, W2 = H

Так как линзу с градиентным распределением показателя преломления сложно изготовить современными средствами нанолитографии, для подобной острой фокусировки ТМ-поляризованной волны можно использовать фотонно-кристаллическую линзу со щелью на оптической оси, аналогичную градиентной линзе по среднему распределению показателя преломления. На рис. 7 а показано распределение показателя преломления в плоскости XZ фотоннокристаллической линзы, аналогичной градиентной линзе (рис. 2).

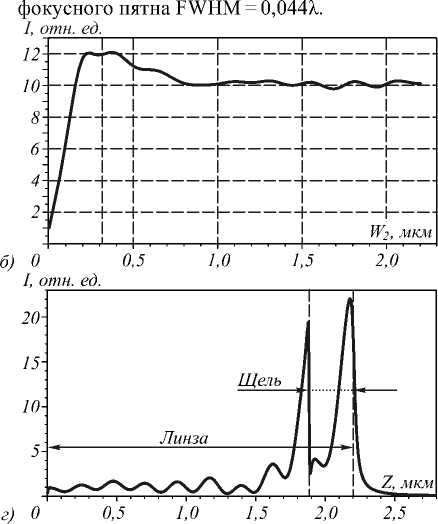
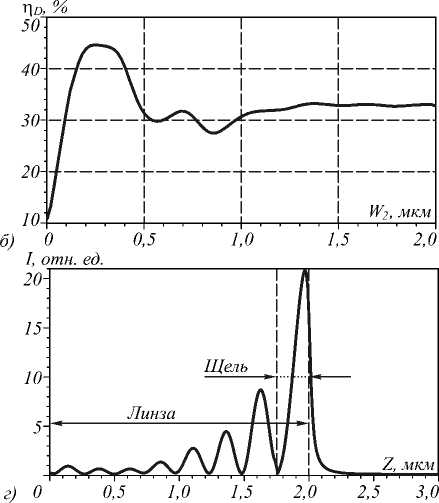
Параметры линзы на рис. 7 а : 8 рядов отверстий вдоль оси Z , 20 рядов отверстий вдоль оси X с шахматным расположением, минимальный диаметр отверстий – 30 нм, максимальный – 250 нм, длина линзы – 2 мкм, ширина – 4,8 мкм, показатель преломления материала линзы n = 3,47, W 1 = 50 нм, W 2 = 0,25 мкм. Для такой линзы зависимость эффективности фокусировки света η _D от длины щели W ₂

при фиксированном значении ширины щели W ₁ = 50 нм выглядит аналогично градиентному ва-

ность фокусировки света в фокусное пятно составляет η _D = 44,3% при W ₂ = 0,25 мкм. Ширина такого

., Л1КМ

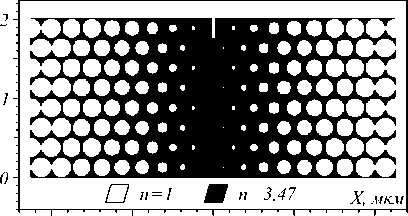
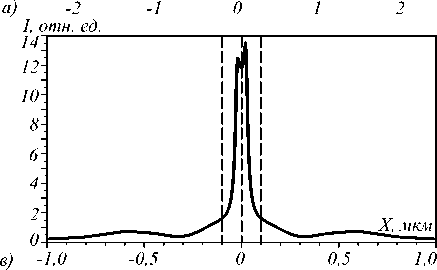
Рис. 7. Распределение показателя преломления в фотонно-кристаллической линзе со щелью (а), зависимость дифракционной эффективности ηD от длины щели W2 при ширине щели W1 = 50 нм (б), распределение интенсивности в фокусе в поперечной плоскости на 10 нм за линзой (в) и на оптической оси (г)

Рис. 6. Зависимость эффективности фокусировки света ηD (а) и интенсивности света в фокусе линзы (б) от длины щели W2 при W1 = 50 нм; распределение интенсивности света на 10 нм за линзой при W1 = 50 нм, W2 = 0,31 мкм (в) и на оптической оси (г)

Заключение

В работе получены следующие результаты:

• 1.    С помощью 2D FDTD-метода показано, что если в планарной градиентной гиперболической секансной микролинзе на основе кремния размером 5×2 мкм сделать наноотверстие на оптической оси шириной 50 нм и длиной около 300 нм, то для падающей плоской волны с ТМ-поляризацией на выходе линзы сформирует-

• ся фокусное пятно с эффективностью ηD =43% и шириной FWHM = 0,035λ = λ/28. Это фокусное пятно меньше всех рассмотренных ранее в работах [1 – 20].

• 2.    С помощью 2D FDTD-метода показано, что планарная фотонно-кристаллическая микролинза в кремнии, являющаяся бинарным аналогом градиентной гиперболической секансной микролинзы с наноотверстием в выходной плоскости на оптиче-

• ской оси шириной 50 нм и длиной 250 нм, фокусирует плоскую волну с ТМ-поляризацией в фокусное пятно шириной FWHM = 0,044λ = λ/23 с дифракционной эффективностью ηD = 44%. Это фокусное пятно также меньше субволновых фокусных пятен из работ [1 – 20].

Работа выполнена при поддержке Министерства образования и науки Российской Федерации (ФЦП «Научные и научно-педагогические кадры инновационной России», соглашение № 8027), грантов Президента РФ поддержки ведущих научных школ (НШ-4128.2012.9) и молодого кандидата наук (МК-3912.2012.2) и грантов РФФИ (12-07-00269, 12-0731117, 13-07-97008).