Гипергеометрические лазерные пучки общего вида и их известные частные случаи

Недавно авторами было рассмотрено новое семейство параксиальных лазерных пучков, комплексная амплитуда которых описывается конфлюэнтной гипергеометрической функцией [1]. Эти гипергеометрические пучки (ГГ-пучки), описываются трехпараметрическим семейством функций и является обобщением двухпараметрического семейства решений параксиального волнового уравнения (типа Шредингера), которые рассматривались в [2]. Также, эти ГГ-пучки [1] являются обобщением ранее рассмотренных гипергеометрических мод [3]. ГГ-моды обладают бесконечной энергией как и известные моды Бесселя, и на практике могут быть реализованы только приближенно. Недавно в [4] были рассмотрены гауссовые гипергеометрические пучки, которые обладают конечной энергией (хотя они уже не являются модами, так как при распространении меняют структуру поперечной интенсивности).

В данной работе показано, что ГГ-пучки являются обобщением гауссовых гипергеометрических лазерных пучков (ГГГ-пучков) [4] и хорошо известных элегантных пучков Лагерра-Гаусса (эЛГ-пучки) [5].

1. Общий вид гипергеометрических пучков

В работе [1] рассматриваются гипергеометрические лазерные пучки (ГГ-пучки), комплексная амплитуда которых описывается трехпараметрическим семейством функций. Эти пучки являются обобщением гипергеометрических мод [4] и двухпараметрических гипергеометрических пучков [2]. В этом разделе мы кратко, следуя [1], повторим вывод ГГ-пучков.

Рассмотрим световое поле с начальной функцией комплексного пропускания вида:

„ / х 1 Г r 1 m Г r 2       , r 1m

E у nm ( r , ф ) = ~HI exP .   ' i Y ln” ⁺ in ф| ’ ⁽¹⁾

2л( wJ ( 2 g w )

от начальной плоскости комплексная амплитуда светового поля, порожденная функцией (1), уже не будет иметь особенности и будет конечной.

При параксиальном распространении светового поля (1) его комплексная амплитуда на расстоянии z будет определяться преобразованием Френеля, которое в полярных координатах имеет вид:

E ( р , 6 , z ) = — ik- JJ E ( r , Ф ,0 ) х

2П z г>2

R                    x                  (2)

■² - 2 р r cos ( ф —0 ) ] f r d r d ф ,

х exp

где (ρ, θ) – полярные координаты в плоскости, отстоящей на расстоянии z от начальной плоскости, k =2π/ λ – волновое число, λ – длина волны.

При вихревом поле во входной плоскости, т.е. при

E ( p , 0 ,0 ) = A ( r ) exp ( in ф ) , уравнение (2) примет вид:

E (р, 0, z) = (—i) n ±1 — expfiH_± in 0) x v x ’ z I 2 z          J

»

\ .l ikr 1 t l k p r ) , x A I r ) exp ---- J ---- r d r .

n

0           1 ² z J 1 z J

Известен справочный интеграл [6]: »                                        v ±a

J x ^{a— 1} exp ( — px ² ) J_v ( cx ) d x = c ^v p ² 2

„| v + a] , / x l v ±a xr ---- г v + 1 . f ----

1 2 J ^{v 71 1}1 2

। — v —1

c ²

4 p

.

где ( r , ф ) - полярные координаты в начальной плоскости ( z = 0), w и у - действительные параметры логарифмического аксикона, □ - радиус перетяжки гауссова пучка, n – целый порядок спиральной фазовой пластинки (СФП) (топологический заряд), m – целое число. Комплексная амплитуда (1) описывает световое поле с бесконечной энергией и с особенностью при r = 0 и m <  0. Несмотря на это в любой другой поперечной плоскости на расстоянии z

Тогда преобразование Френеля от (1) имеет вид:

Eуnm (p,0 z) = 2^n !pwm±iy x n±1—2

Г ikp 1 l ikp. xl--| expl------+ in0 |x

1 2 z J I 2 zJ

n + m +2+ i у

Г 1 ik ।      ²

x

1 2 g ²  2 z J

n + m + 2 + i у

Fl n±m ±2± i l lx

I k p 1 2 z

2 g ²

ik

2 z

.

Обозначим z ₀ = k с ² , q = ( 1 - iz ₀ / z ) ¹² . Тогда вместо (5) получим:

При у = 0 вместо (11) получим в безразмерных единицах:

Eynm (Р, 0 z) =

хт f а. i 2п n ! ( zq ² J

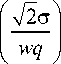
( - i ) n ^{+ 1}     1 m ⁿ

E 0 nm ( P ', Ф', z ) =^---TF“^{Z 2} ( ^Z- ¹ )

2 n n ! Z - 1

m + n

2 X

) ⁿ           2

ikp   . „ О n + m + 2 + i у)

exp —— + in0 Г ---------- x /£\

( 2z      J L 2 J (6)

Г i p' ²         1

xp exp I-^ + in Ф IГ

n + m + 2 ) x

n + m + 2

P' ² 1

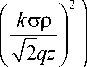
z(z-1 )J’

Выражение (6) описывает комплексную амплитуду параксиальных гипергеометрических лазерных пучков общего вида. Сокращенно: ГГ-пучки. Модуль комплексной амплитуды (6) пропорционален функции Куммера:

где

[^p ' = r y w ,

5 = z/z0, z 0 = kw2/2,

. q ² = ( Z- 1)/ Z -

n

|Eуnm (Р,0z)| ~ x2|iF(a,b,-x)|, где x - комплексный аргумент:

Г ,     А2

I kcp I x = Т- .

L V2 qz J

Положим в (13) m = n + p и воспользуемся известным соотношением для конфлюэнтной гипергеометрической функции [7]:

1 F ( a , b , - x ) = exp ( - x ) 1 F ( b - a , b , x ) , (14)

тогда вместо (12) получим:

Функция Куммера или конфлюэнтная гипергеометрическая функция имеет вид [7]:

E 0, n , n + p ( P ', Ф ', ^z ) =

где

X

1 F 1 ( a , b , - x ) = £ C i ( - 1 ) l x¹ ,                      (9)

I = 0

P I p 1

XZ² ( Z- i )i ^{n + 1 + 2 J}

C = ^Г ( a ^{+ 1} ) ^Г ( ^b )

¹     Г ( a ) Г ( b + 1 ) 1 !’

- P

Г ( x ) - гамма-функция.

2. Гауссовые гипергеометрические пучки

В работе [4] рассмотрены гауссовые гипергеометрические пучки (ГГГ-пучки). Эти пучки обладают конечной энергией, но при распространении в пространстве, в отличие от ГГ-мод [3], они меняют вид поперечного распределения интенсивности, оставаясь радиально-симметричными пучками. Эти пучки не образуют ортогональный базис, в отличие от ГГ-мод. Покажем, что ГГГ-пучки являются частным случаем ГГ-пучков. Перепишем (6) с новым обозначением w = 72 с :

E у nm ( r ' , ф' , z ) =

( - l ) n ^{+ 1} 2 n n !

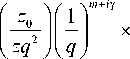
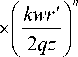
f ikr '² . X exp I-----+ in ф IГ

L 2 z       J

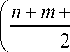
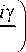
x (11)

n + m + 2 + i у

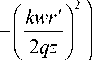
I p 1

/ A n + 1 Г n + 1 +—

(-1)      L________2 J

____________ x

2 п     Г ( n + 1 )

p' ⁿ exp ---- + in ф'

LZ- 1

p' ²    1

z(z-i )J'

Выражение (15) отличается от аналогичного выражения, полученного в [4] (кроме константы), только знаками перед мнимой единицей в Z - i ,

( - i ) ” ^{+ 1} и i p' ² . Действительно, в [4] рассмотрены ГГГ-пучки с комплексной амплитудой:

I HyGG\m = Upm (p, Ф, Z) = г|1 + m|+p 1     p

= C pm X ■ ,^{2 J} i^' ⁺¹Z ² ( Z + i Г¹"¹ ^ + p^{1 2]} X

^{Г( 1 +} m l)                               (16)

xp m l exp |^- i p² /( Z + i ) ] exp ( im ф ) x

I

x1 FI -у,ml+1;

Z ( Z+ ⁱ ) ^J

3. Элегантные пучки Лагерра-Гаусса

Для того чтобы показать, что эЛГ-пучки [5] являются частным случаем ГГ-пучков, перепишем выражение для ГГ-пучков общего вида (6) при m = - 1 и с учетом соотношения (14), выделив явно гауссову экспоненту:

^E Y, n ,-1

( р , 6 , z ) =

( - 1 ) n + 1

z ₀

2 п n !

zq ²

X

Выражение (21) имеет вид, несколько отличный от общепринятого вида элегантных пучков ЛГ [5]

У2 a

■ 1+ i у

kap

n

хГ

wq

2 qz

(ik p ²   . )

exp ---- + in 6 x

I 2 z         J

n + 1 + i у

exp

n + 1 - i у 2

kap

2 qz

X

f     A p ⁺¹< - 2    A2

ZT / A \ / Л p ⁺¹ I   ^z o   I I i ^ ^z o  I

E ⁽p ^{, 6 ,} z ) = ^(- i ) I |     I--2-2°" I ^X

( q z J  ^ w q z J

n

I ik p ²1² ( 2 q ² z J

, n + 1,

k ap

2 qz

Далее воспользуемся известным соотношением для конфлюэнтной гипергеометрической функции [7]:

1 F i ( ^- n ^, a + 1, x ) = n ^! Й^а ( x ) ^{, (a +} У n

где L n '¹ ( x ) - присоединенные многочлены Лагерра, ( a + 1 ) n - символ Похгаммера. Из сравнения (17) и (18) видно, что для того, чтобы получить моду Ла-герра-Гаусса с индексами ( p , 5 ) , нужно чтобы выполнялись равенства:

f n + 1 = 5 + 1,

) n + 1 - i у --------= - P .

I 2

При условии (19) вместо (17) получим:

. ( - i ) ⁵ +1 I I

E . s   (p, 6, z ) =------ —7 х

^- i ( ^{5 + 1}+² p ) , ⁵ , ^- 1 ^{( ,} )      2 _Л 5 ! ( zq ² J

wq

-1 + 5 + 1 + 2 p / N5       /2A

I I kap I        [ ikp     ._ I

— exp --- + is 6 x

I (V2qz J     ( 2zJ

I 5 + 1 + 5 + 1 + 2 p хГ1 ----------------

exp

k ap I

У2 qz J

5 + 1 - ( 5 + 1 + 2 p )

, A²I k ap I

У2 qz J

.

После несложных преобразований с учетом (18) вместо (20) окончательно получим:

^E - 1 ( 5 +1+2 p ) , 5 ,-1 ^{(p 6 , z} )

/ A ^{5 +1} 1 Z X         A ^{5 +2 p} / , A ⁵

( ^- i ) ^{p !} | z 0 || У 2 a I I k ap I

2 n   ( zq ² J^ wq J   ( У2 qz J

I ikp2    . n | rn exp —— + in6 L„ p

( 2 q z J

I ik p ² 1

I 2 q ² z J

I ik p      . „ L( 5)

x exp —— + 15 6 \Ev p

( 2 q z J

k ap I

У2 qz J

.

Выражение (22) имеет форму x n ² exp ( - x ) Lⁿ _p ( x ) , а форма выражения (21) отличается от (22) постоянными множителями и аргументом полинома Лагер-ра. Таким образом, обнаружена еще одна разновидность элегантных пучков ЛГ, которые являются частным случаем ГГ-пучков.

4. Численное моделирование

При численном моделировании преобразование Френеля от поля (1) вычислялось по методу прямоугольников и сравнивалось со значениями, получаемыми при использовании формулы (6). Таким образом было проверено полученное выражение (6).

Результаты моделирования приведены на рис. 1. Были использованы следующее значения параметров: длина волны X = 633 нм, радиус перетяжки Га-уссового пучка a = 1 мм, порядок СФП n = 3 , показатель степенной составляющей амплитуды m = 0, расстояние вдоль оптической оси z = 500 мм.

Из рис. 1 видно, что при дифракции Гауссового пучка на СФП и логарифмическом аксиконе формируется кольцевое распределение интенсивности с дополнительными боковыми лепестками (кольцами). Радиус первого кольца и энергию боковых лепестков можно изменять, меняя параметр у .

На рис. 2 показаны радиальные распределения модуля амплитуды для элегантных пучков Лагер-ра-Гаусса при распространении в свободном пространстве. В выражении (21) были использованы следующее значения параметров: длина волны Х = 633 нм, радиус перетяжки Гауссового пучка a = 10 мкм, порядок СФП n = 3 , показатель степенной составляющей амплитуды m = - 1, параметр логарифмического аксикона у =- 12 i (т.е. пучок эЛГ имеет индекс (4, 3)).

Такие картины дифракции могут быть получены про прохождении Гауссового пучка через спиральную пластинку и амплитудный фильтр с пропусканием, пропорциональным степенной функции p ¹¹ .

Из рис. 2 видно, что элегантные пучки ЛГ не являются модами, т.к. структура поперечной интенсивности меняется (хотя и не сильно). Видно также, что энергия боковых лепестков существенно меньше, чем на рис. 1.

\E\ 0,18

0,10

0,02

а)

\E\ -0,16

\E\

0,14

V JL

0.08

0,02

б)

1    2    3    4 p.mm

в)

2   3   4 p,mm

Рис. 1 Модуль комплексной амплитуды, описывающей дифракцию Френеля от функции (1), вычисленные с помощью интеграла (3) и аналитической формулы (6) при m = 0: у = 0 (а), у = 5 (б), у = 20 (в)

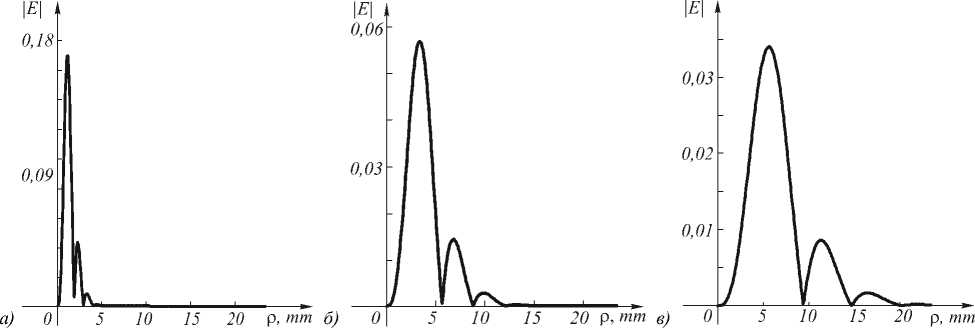
Рис. 2 Распространение элегантных пучков Лагерра-Гаусса.

Радиальные распределения модуля амплитуды при z = 100 мм (а), z = 300 мм (б), z = 500 мм (в)

Заключение

В работе показано, что полученное недавно трехпараметрическое семейство точных решений параксиального волнового уравнения (типа Шредингера), которое названо гипергеометрическими лазерными пучками, включает в себя как частные случаи известные семейства лазерных пучков: гауссовые гипергеометрические лазерные пучки и элегантные пучки Лагерра-Гаусса.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-Sa-06), а также гранта РФФИ 05-0850298 и 07-07-97600.