Гипергеометрические лазерные пучки в параболическом волноводе

В 2007 году были рассмотрены параксиальные гипергеометрические моды (ГГ-моды) [1]. Немного позже на основе ГГ-мод были получены гипергеометрические гауссовые лазерные пучки [2]. В [3] рассмотрено более общее семейство ГГ-пучков, которые включают в себя как частные случаи ГГ-моды [1] и гипергеометрические гауссовые пучки [2]. Лазерные ГГ-пучки были экспериментально сформированы с помощью дифракционных оптических элементов [4] и голограмм, синтезированных на компьютере [5]. Недавно получены аналитические выражения, описывающие распространение ГГ-пучков в градиентной гиперболической среде [6] и одноосном кристалле [7].

В этой работе получено выражение, описывающее распространение ГГ-пучков в 3D градиентном параболическом волноводе. Показано, что световое поле ГГ-пучков периодически повторяется, а через каждые полпериода формируется Фурье-спектр.

Также было получено новое семейство модовых решений для уравнения Гельмгольца в параболической среде. Эти решения пропорциональны функциям Куммера и расходятся на бесконечности. Однако при некоторых значениях параметров функции Куммера эти решения становятся конечными и переходят в известные моды Лагерра–Гаусса (ЛГ-моды).

В последнее время возрос интерес к градиентным элементам микрооптики. Так, в [8–10] рассматривалась градиентная микролинза Лунеберга. В [8,9] были проведены эксперименты с планарной линзой Лунеберга, а в [10] моделирование планарной фотонно-кристаллической линзы Лунеберга показало, что сформированный ею фокус имеет ширину по полуспаду интенсивности FWHM = 0,44λ при n ₀= 1,41. В [11, 12] рассмотрена планарная, а в [13] – трёхмерная линзы Микаэляна с градиентным показателем преломления в виде гиперболического секанса. В [13] показано, что 3D градиентная линза

Микаэляна формирует фокальное пятно с диаметром по полуспаду интенсивности FWHM = 0,40λ. В [14] рассмотрена планарная субволновая бинарная линза Микаэляна, формирующая фокус шириной FWHM=159 нм =0,102λ =0,35λ / n , n =3,47 – показатель преломления линзы.

В этой работе рассмотрено распространение гауссова пучка в градиентном параболическом волокне. Участок этого волокна определённой длины можно рассматривать как градиентную параболическую (ГП) линзу. Моделирование показало, что фокусное пятно в такой линзе имеет диаметр FWHM=0,42λ, при n 0 = 1,5 – показатель преломления на оси линзы. Получено также аналитическое выражение для радиусов скачков показателя преломления для бинарной линзы, аппроксимирующей 3D ГП-линзу. Рассчитанный FDTD-методом меньший диаметр эллиптического фокусного пятна такой бинарной параболической линзы FWHM=0,45λ .

1. Параксиальные гипергеометрические пучки в параболической градиентной среде

Рассмотрим параболическую градиентную среду с показателем преломления вида:

n 2 ( r ) = n 02

1 -

( n ₀ ²

-

n

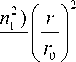
где r – радиальная поперечная координата, n ₀ и n ₁ – показатели преломления на оптической оси ( r =0) и при r = r ₀. На рис. 1 показан профиль показателя преломления (1).

Параксиальное уравнение распространения света в параболической среде (1) имеет вид:

_ d d2 d2         (x2 + y2)

2ik —i—^ч---—(ak) ------ dz dx2   dy2 ( )      4

X E ( x , y , z ) = 0,

X

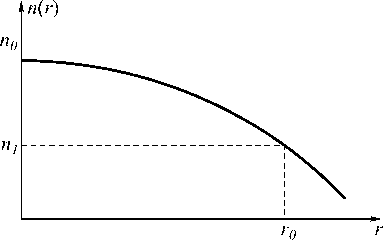
Рис. 1. График зависимости параболического показателя преломления от радиальной координаты

L

J у ^Ц-1 exp ( -в у ² ) J_n ( cy )d y = 0

c р - ( n +ц )/2 Г

2 ^{n +1} n !

n + Ц I

2 ^J

----x x

ⁿ 02 -

где а =------ r ₀ n ₀

n 2        2 п

—, k = — n0, ^k - длина волны. В

[15] показано, что общее решение (2) имеет вид:

а к

E ( x, y, z ) =----------- х

2 п i sin( T z )

i а к /2    2 а

^Х exP 1, , J x ⁺ У ) ^Х

_ 4 tg ( t z )^x          _

£            14sin(Tz)_ x cos(tz) - 2( x ^ + yn)]} d^ dn,

где T = а /2 . Заметим, что интегральное преобразование (3) с точностью до обозначений совпадает с частичным преобразованием Фурье [16, 17]. В цилиндрических координатах уравнение (3) для начального поля E 0 ( r , ф ) = E 0 ( r ) exp( in ф ) имеет вид:

E (р, 6, z) = (- i) n+1^ x f2

Г ikP2      I x exp     + in6 x

I 2 f l        J

L             ( .1 2 A f 1 _\

I ikr I r I krр I x E0( r )expl — I J.      Ird r ,

0 I ² f l JI ^f 2 J

где n – целое число, J n ( x ) – функция Бесселя,

f l = f ) tg ( z / f ) ),

^f 2 = ^f ) ^Sin( z / ^f ) ),

f ) ⁼

а

r ₀ n ₀

^ И 0 ^- n i

В [18] получены выражения, описывающие преобразования пучков ЛГ в параболическом волокне. Далее мы рассмотрим распространение в параболическом волокне (1) ГГ-пучков, которые в начальной плоскости описываются комплексной амплитудой [3]:

/ x m + i y      /     2 A

I r I I r I

E 0 ( ^r ) = l 7 I     exP l ^-I ,                        ⁽⁶⁾

I 8 J         I 2 о J

где m, y — действительные числа , 5 и о - масштаб степенной амплитудной составляющей и радиус гауссова пучка. Подставим выражение (6) в (4) и воспользуемся справочным интегралом [19]:

^x 1 F l

Г n + Ц ,

I ^, n + ¹, ^-

c ² 1

40 J ,

где Г ( x ) – гамма-функция, 1 F 1( a, b, x ) – функция Куммера [19], тогда получим вместо (4):

E m у n ( P , 6 , z ) =

= (-i )

/      , x / i—  X m+i Y n+1Г 2 k о21Г V2c I

Il —— I x

f2 JI i ikP2        1

x exp      + in 6 x

I 2 f 1        J

x| 1 -

Г x—

-. x - ( m + i у+ 2)/2

ik о |

x f J n + m + i у+ 21

x

x x^{n /2}

где

x =

1 F 1

n !

n + m + i y+ 2

, n + 1, - x I ,

P ² + ^ik P ² 2 и ²( z ) 2 R ( z ),

ю ( z ) = о cos

1/2

(тАГгЛ ²   (  \

'² — +     2" sin ² —

I f ) J  I k о² J      | f ) J

,

1 Г 2 z I I f I ² A z ) R ( z ) = — f sin — x 1 + —- tg ² —

²       I ^f ) J      I ^{k о}J    I ^f ) J

Световое поле (8) по модулю будет повторяться с периодом L = π f ₀. Амплитуды в плоскостях, разделённых между собой расстоянием в половину периода L 1 =(π f 0 ) /2, связаны преобразованием Фурье:

n + 1 [ k о |

^Em у n ⁽ P , ⁶ , z = ^L1 ) = ( - ⁱ ) H-| ^X

I ^f 2 J

XI 8

m + i у

I     exp ( in 6 ) x

Г Г n + m + i у+ 2

X

^x 1 F 1

2      > n!

n + m + i у+ 2

n /2

P ² I 2 to f I --<— x

, n + 1, -;Py

2«> 2

,

где o^ = f 0 / k о - эффективный радиус светового поля в плоскости Фурье. Световые поля (8) ортогональны между собой при разных значениях топологического заряда n . Заметим, что при f 0 = k σ²

реальная часть аргумента функции Куммера перестаёт зависеть от расстояния z : m ( z ) = о = const , а мнимая часть аргумента продолжает оставаться зависимой от переменной z : R ( z ) = (1/2) f ₀tg ( z / f 0 ). Поэтому и амплитуда всего поля (8) будет зависеть от z . Поэтому ГГ-пучки (8) не являются модами параболической градиентной среды ни при каких параметрах и значениях номеров m, n, γ, за исключением гауссова пучка ( m = n = γ = 0).

, х I r2 I , E (r, ф, z ) = r exp I--- I exp (± in ф)x

V ®2 J

2. Моды параболической градиентной среды

Рассмотрим параболическую градиентную среду вида (1) n ² ( r ) = n 2 (1 — T ² r ² ), где T = a /2. Будем искать решение уравнения Гельмгольца для параболической среды

, „ X                  . 2 r ²

^x exp ( i ^в z ) 1 F 1 ^— s , n + 1, -^ 2- =

s! „ I r2 )

= 7---7T ^{r e}xp |--Г I^x

(n + 1) s        V ®2 J x C     12 r2)

x exp ( ± in ф ) exp ( 1 в z ) L I —- I ,

V m2 J

где

в = kn 0

1---(2s + n +1) .

kn ₀

d2 +1 _э_ + £ d2 dr2 r dr r2 Эф2

2 d 7 2 2 / \

+ , 2 + k0n (r) Ix dz             J

xE (r, ф, z) = 0

c показателем (1) в модовом виде:

| r2 |

E (r, ф, z) = rpzq x exp--- exp (inф)x m2

2 ,

x exp (iвz) F (r*zl)

где F – некоторая функция, а β – константа распространения моды. Можно показать, что решением уравнения (11) будет семейство функций:

Если радиус гауссова пучка моды ЛГ (16) не удовлетворяет условию m ₂ = ^ 2 / kn ₀ T , то пучок ЛГ уже не будет модой. Распространение немодового пучка Лагерра–Гаусса в параболической среде рассмотрено в [18].

Таким образом, в данном разделе показано, что существует широкий класс модовых решений уравнения Гельмгольца в цилиндрической системе координат для параболической среды, но только те решения из этого класса будут обладать конечной энергией (то есть будут физически реализуемы), которые совпадают с модами Лагерра–Гаусса.

E ( r , ф , z ) = r n exp

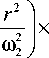
x exp (± in ф) exp (i в z) x

3. Параболическая градиентная микролинза

В семейство решений (8) входит как фундаментальный пучок гауссов пучок, амплитуда которого также периодически повторяется при распространении в параболическом градиентном волокне (1). Из (8) при n = m = γ = 0 можно получить:

^x i F 1

n + 1 ® ²       ,2 2l 1 2 r ²

— + -2 ( ^{в —} k n о ) , n + 1,—

2      8                       CO 2

где 1 F 1 ( a, b, x ) – по-прежнему функция Куммера, m ₂ = ^ 2 / kn ₀ T . Так как функция Куммера имеет следующую асимптотику при ^ ^ ^ [20]:

x exp

—

P ² 2 m ² ( z )

E 0 ( p , 6 , z ) = ( — i )

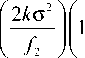
f 1

ik о ²

—

ik p ² ) 2 R 1 ( z ) J ,

— 1

x

1 F 1 ( a , b , ^ ) =

= Г ^ exp®£, a ^— b ( 1 + O (1/ ^ ) ) , Г ( a )

где O ( x ) – стремится к нулю быстрее, чем x , то функция (13) будет расходиться при r ^^ . Во множестве решений (13) есть и нерасходящиеся решения. Если у функции Куммера первый параметр равен целому отрицательному числу, то функция Куммера становится равной многочлену, а решение (13) сходится к нулю при r ^^ . То есть при условии:

n + 1 ^2 / О 2 7 2 2 А                                  /1 \

— + -2 ( в ² — к ² n о² ) = — s                  (15)

где

^R 1^{—1 ( z} ) = [ ^cos ^{2 ( z} / ^f 0 ) +

2       ²

+1 ^°У I sin ² ( z / f ) — 1 /

V k о ² J ⁰

/ { f ) *g ( ^z / f 0 ) [ ^cos ^{2 ( z} / f 0 ) +

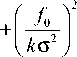
sin ² ( z / f ₀)

вместо (13) получим известные моды Лагерра– Гаусса:

Из (18) и (19) следует, что при f , = k о ² гауссов пучок распространяется в параболическом волокне без изменения, сохраняя свой диаметр. Если f , ^ k о ² , то радиус гауссова пучка меняется по формуле:

1/2

f J

®(z) = О cos21 I +1 —7 I sin21 II f0 J I kО J     I f0 J

,

из которой следует, что минимальный радиус, равный ц = f 0 / k о (если f 0 <  k g ² ), достигается на расстоянии L 1 = n f 0 /2 от начала ( z = 0). При этом диаметр гауссова пучка по полуспаду интенсивности будет равен:

FWHM = ^{f 2122 1} ^ r⁰ n ⁰ . (21) I ^п J С,]П 02 - П 2

Таким образом, можно рассмотреть градиентную параболическую линзу как отрезок параболического волокна с радиусом r0 и длиной вдоль оптической оси L1 =(πf0) /2. Такая ГП-линза будет фокусировать падающий на её входную поверхность плоский гауссов пучок с радиусом σ в фокусное пятно с диаметром (21), которое сформируется вблизи выход-

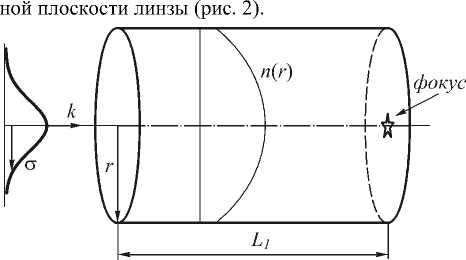
Рис. 2. Схема фокусировки гауссова пучка с помощью ГП-линзы

Из (21) следует выражение для числовой апертуры ГП-линзы ( n ₁ = 1):

NA = - T n "³!.                         (22)

r ₀

При σ = r ₀ числовая апертура (22) совпадает с NA для планарной линзы Микаэляна [12]. Например, при n ₀= 1,5, n ₁ = 1, σ = r ₀ получим следующие значения длины ГП-линзы L 1 = 2,1 r ₀ и диаметра фокусного пятна FWHM=0,36λ. Это немного больше, чем дифракционный предел в среде с показателем преломления n ₀ = 1,5: FWHM = 0,34λ. Однако так как при выводе (21) предполагается, что линза имеет по радиусу неограниченные размеры и показатель преломления (1) спадает на бесконечности до нуля, то такое значение ширины фокуса (FWHM=0,36λ) нельзя реализовать на практике, когда реальная линза ограничена радиусом r 0 , при котором n ( r 0 ) = 1.

• 4.    Бинарная параболическая линза

Градиентную параболическую линзу можно приближённо поменять на бинарную параболическую линзу по правилу, схематично изображённому на рис. 3.

Согласно рис. 3 радиус ГП-линзы r0 разбивается на N равных отрезков длиной А : r0 = NА, тогда ра- диусы начала и концов этих отрезков равны: rp = pА,p = 0,1,2,N-1.

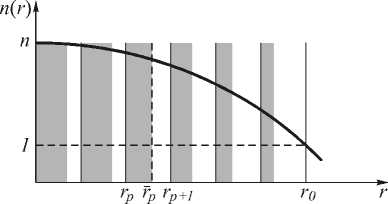
Рис. 3. Схема замены непрерывной параболической зависимости показателя преломления на кусочнопостоянную (бинарную) зависимость

Начало p -го бинарного кольца совпадает с радиусом r_p , а конец p -го бинарного кольца r _p находится из уравнения:

^r p +1    ________________

2      2          2    2                   22

( r p + 1 r p ) ⁺ n 0 ( r p ' p ) ^{2 n} 0 J V^{1 T} ' r d ' . ⁽²³⁾ r p

Из уравнения (23) можно получить явное выражение для радиуса конца p -го бинарного кольца:

-2_ ( n 0 r ^{2 -} Г 2 + 1         2 n 0

'n =1^

p      ( n 0 - 1)     3( n 0 - 1) T ²                     (24)

x[(1- (Trp )2 )3/2 -(1- (Trp+1)2 )3/2 ] , p = 0,1,2,..., N -1.

Заметим, что в (24) радиусы скачков показателя преломления r p можно выбирать не эквидистантными и учитывать минимальный технологически возможный размер зоны.

• 5.    Результаты моделирования

  • 5.1.    Планарная градиентная параболическая линза

Для начала рассмотрим двумерный случай линзы. Моделировалась фокусировка ТЕ-поляризован-ной падающей волны методом FDTD в коммерческой программе FullWave (Rsoft Design Group). Сетка разбиения отсчётов по оптической оси Z и поперечной оси X была λ/130 (4,1 нм), шаг по времени Δ( cT) =2,8 нм.

На рис. 4 представлен показатель преломления в линзе в градациях серого. Радиус линзы r 0 = 1 мкм, n o =1,5, a =1,49 мкм^-1, X = 0,532 мкм. Так как a = 2/ f 0 , то f 0 = 2/ a= 1,342 мкм, длина линзы L 1 = ( п / 2) f 0 = ( п / a ) = 2,1 мкм.

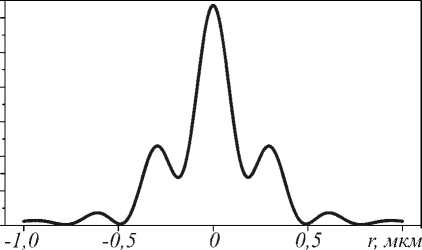
На рис. 5 представлено распределение интенсивности электрической компоненты на расстоянии 10 нм за линзой при плоской падающей волне и гауссовом пучке с радиусом σ = 1 мкм.

Ширина фокусного пятна по полуспаду интенсивности равна FWHM = 0,388λ =0,2 мкм в случае плоской падающей волны и FWHM = 0,5λ = 0,27 мкм в случае гауссова пучка. Как видно из рис. 5, макси- мумы интенсивности рядом с основным фокусным пятном около 30%, что свидетельствует о неоптимальной длине линзы.

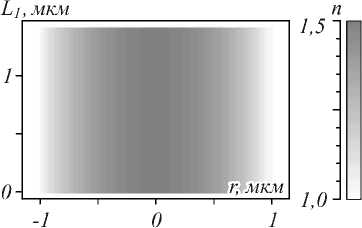
Рис. 4. Показатель преломления в градиентной бинарной линзе в градациях серого (L1 = 1,56 мкм) I, отн. ед.

1,2

1,0

0,8

0,6

0.4

0,2

О а)

I, отн. ед.

0,6

0,4

0,2

О б)

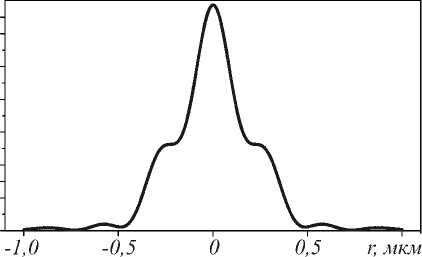
Рис. 5. Распределение интенсивности (|E|2) в фокусной плоскости в 10 нм за линзой в случае плоской падающей волны (а) и гауссова пучка (б)

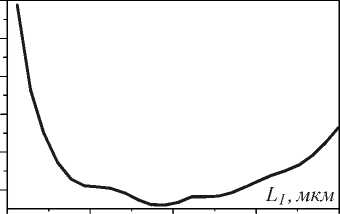
Можно достичь более острой фокусировки, изменив длину линзы. На рис. 6 показана зависимость ширины фокусировки света линзой FWHM в длинах волн от длины линзы L 1 .

Как видно из рисунка, минимальная ширина фокусного пятна для гауссова пучка и плоской волны достигаются при различной длине линзы L ₁. Наилучшая фокусировка плоской волны достигается при значении L ₁ = 1,56 мкм, при этом FWHM = 0,375λ, а минимальное фокусное пятно при гауссовом падающем пучке составляет FWHM=0,394λ при длине линзы L ₁ = 1,73 мкм. В этом результате проявляется общая закономерность при фокусировке лазерного света: при прочих равных условиях увеличение боковых лепестков (рис. 5 а ) сопровождается уменьшением ширины фокусного пятна (и увеличением глубины фокуса).

• 5.2.    3D градиентная параболическая линза

В трёхмерном случае моделировалась линза с градиентным показателем преломления в плоскости

XY , зависящим от радиуса r . Градиентное распределение показателя преломления трёхмерной линзы в плоскости XY представлено на рис. 7.

FWHM, в длинах волн 0,48 0,46 0,44 0,42 0,40 0,38

а)     1,2      1,4      1,6      1,8     2,0

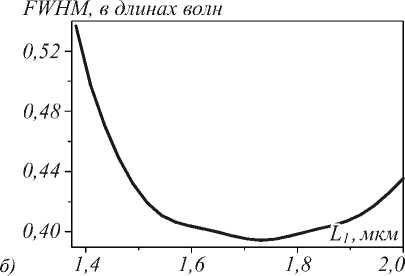
Рис. 6. Зависимость ширины фокусного пятна в 10 нм от выходной плоскости линзы от длины линзы L 1 для плоской волны (а) и гауссова пучка (б) на входе линзы

Y, мкм п=1,5

• -1 -                 X, мкм

• -1          0           1     1,0

• 5.3.    3D бинарная параболическая линза

Рис. 7. Градиентное распределение показателя преломления линзы в плоскости XY в градациях серого

При моделировании трёхмерного случая использовалась сетка отсчётов λ/40 (13,3 нм) по всем трём осям. Моделировалось распространение линейно-поляризованного света через линзу (основная компонента падающего поля E_y ), падающая волна – плоский гауссов пучок с радиусом σ = 1 мкм. На рис. 8 а представлена зависимость ширины фокусного пятна FWHM от длины линзы L ₁, измеренная через центр фокусного пятна вдоль оси X .

Видно, что минимум достигается при длине линзы L ₁ = 1,6 мкм, при этом ширина фокуса вдоль оси X равна FWHM=0,42λ. Распределение интенсивности (| E |²) в фокусном пятне линзы при этих параметрах представлено на рис. 8 б . За счёт линейной поляризации фокусное пятно вытягивается вдоль оси Y и составляет FWHM = 0,70λ.

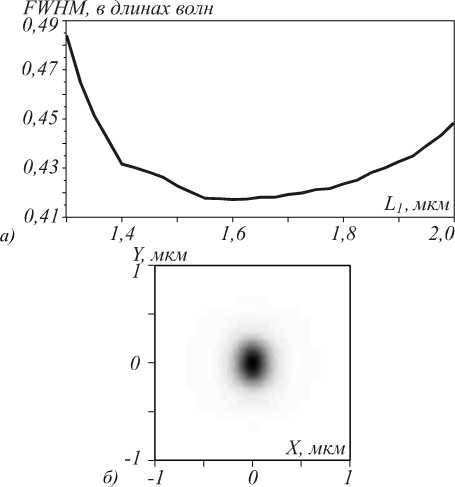
Рис. 8. Зависимость диаметра фокусного пятна вдоль оси X в 10 нм от выходной плоскости линзы от длины линзы L1 для линейно-поляризованного гауссова пучка на входе линзы с радиусом σ=1 мкм (а) и распределение интенсивности (негатив) в фокусном пятне линзы при оптимальной длине L1=1,6 мкм (б)

На практике сложно изготовить линзу с градиентным непрерывным профилем показателя преломления. Бинарную же микролинзу можно изготовить по технологии изготовления 3D фотонно-кристаллических волноводов или волноводов Брегга [21]. На рис. 9 представлено бинарное распределение показателя преломления в плоскости XY бинарной линзы (24), аппроксимирующей градиентную параболическую линзу.

Y, мкм

• -1 -                X, мкм

• -1           0           1

Рис. 9. Бинарное распределение показателя преломления линзы в плоскости XY. Тёмный цвет соответствует показателю преломления n=1,5, белый – n=1

Такая линза будет фокусировать свет немного хуже варианта с непрерывным изменением показателя преломления (1). На рис. 10 показано распределение интенсивности в фокусной плоскости бинарной параболической линзы и сечения этого распределения через центр вдоль осей X и Y . Длина линзы выбрана оптимальной и равна L 1 - 1,9 мкм (параксиальная теория даёт немного большее значение

L ₁ =2,1 мкм). Падающее линейно-поляризованное поле с плоским волновым фронтом имеет гауссово распределение интенсивности с радиусом σ = 1 мкм. Минимальный размер зоны (разница между соседними радиусами скачков показателя преломления) бинарной линзы равен 35 нм. При моделировании использовалась сетка отсчётов λ/70 (7,6 нм) по всем трём осям. Начальная плоскость поляризации параллельна плоскости ZY .

Y, мкм

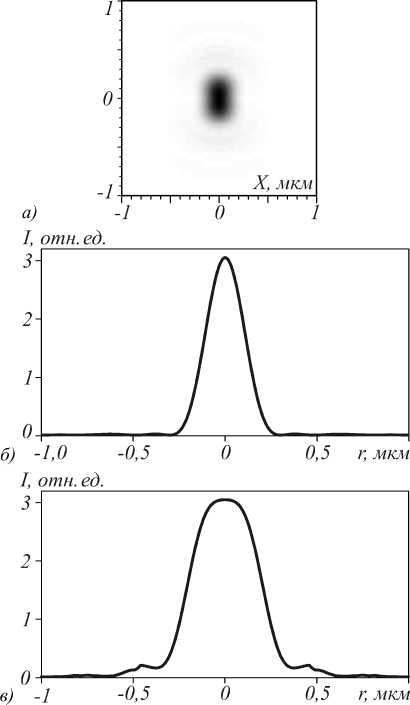
Рис. 10. Распределение интенсивности (негатив) в фокусной плоскости бинарной параболической линзы на рис. 9 (а) и сечения интенсивности через центр фокусного пятна вдоль оси X (б) и Y (в)

Диаметр фокусного пятна по полуспаду интенсивности (для рис. 10) вдоль оси X FWHM=0,45λ, вдоль оси Y FWHM=0,78λ. Фокусное пятно вытянуто вдоль оси Y и почти не имеет боковых лепестков. Напомним, что параксиальная теория даёт диаметр фокусного пятна, FWHM=0,36λ.

Заключение

Основные результаты данной работы:

• •    получено выражение для комплексной амплитуды семейства параксиальных гипергеометрических лазерных пучков, распространяющихся в градиентном параболическом волокне (уравнение (8));

• •    найден широкий класс модовых решений уравнения Гельмгольца в цилиндрической системе координат для градиентной параболической сре-

• ды; эти решения пропорциональны функциям Куммера (уравнение (13)); показано, что только те решения из этого класса будут обладать конечной энергией (то есть будут физически реализуемы), которые совпадают с модами Лагерра– Гаусса (уравнение (16));

• •    отрезок определённой длины градиентного параболического волокна рассмотрен как параболическая линза, для которой получены выражения для числовой апертуры и для диаметра фокуса по полуспаду интенсивности (уравнения (21),(22));

• •    моделирование FDTD-методом фокусировки линейно-поляризованного гауссова пучка с помощью 3D градиентной параболической линзы показало, что оптимальная длина линзы меньше, чем предсказывает скалярная теория, и при этом меньший диаметр эллиптического фокусного пятна FWHM=0,42λ (рис. 8 б );

• •    получена явная формула для радиусов колец бинарной 3D линзы, аппроксимирующей градиентную параболическую линзу (уравнение (24));

• •    рассчитанный минимальный меньший диаметр эллиптического фокусного пятна такой бинарной 3D линзы FWHM=0,45λ (рис. 10).

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (госконтракт № 14.740.11.0016), грантов Президента РФ поддержки ведущих научных школ (НШ-4128.2012.9) и молодого кандидата наук (МК-3912.2012.2) и грантов РФФИ (12-07-00269, 12-0731117).