Гипергеометрические пучки в ближней зоне дифракции в рамках скалярной модели

Гипергеометрические (ГГ) моды, рассмотренные впервые В. В. Котляром с соавторами [1-3], являются одним из типов модовых решений параксиального волнового уравнения в цилиндрических координатах. Эти решения описывают семейство световых полей, которые сохраняют свою структуру при распространении, изменяясь только масштабно.

Свойства нового типа мод интенсивно рассматривались как той же группой авторов [4-10], так и другими учеными [11-13].

Данные моды отличаются от известных параксиальных мод (гауссовых, бесселевых) тем, что их основной радиус увеличивается как корень квадратный от пройденного расстояния (а не пропорционально ему) и расстояние между соседними максимумами (или минимумами) в картине дифракции обратно пропорционально радиальной координате (а не эквидистантны, как у бесселевых).

ГГ моды, как и параксиальные моды Бесселя, обладают бесконечной поперечной протяженностью и энергией. На практике из-за поперечного ограничения их можно сформировать только приближенно и на конечном отрезке вдоль оптической оси. Однако более компактное, чем у бесселевых мод, распределение энергии (за счет уменьшающегося периода колец) позволяет ГГ модам дольше сопротивляться дифракционным искажениям, связанным с необходимостью обрезать моду до некоторого радиуса. Исследования показали, что отрезок бездифракционного распространения ГГ мод может увеличиваться в несколько раз по сравнению с бесселевыми модами, имеющими такой же размер центрального кольца [14].

Тем не менее, физическая реализация ГГ мод имеет дополнительные сложности: амплитуда и фаза в начальной плоскости (z=0) имеют особенности в центральной точке (при r=0), что приводит к необходимости также вырезать или аппроксимировать центральную область. Также резкий спад амплитудной функции при росте радиальной координаты за- трудняет применение методов кодирования амплитудной информации в фазовую – периферийная часть прописывается очень плохо даже при большом числе уровней квантования. Приходится искать компромисс [14] между точностью воспроизведения ГГ моды и ее энергетической эффективностью, т.к. основная часть энергии сосредоточена в центральной (проблемной) области.

Наиболее энергетически эффективным решением является игнорирование амплитудной информации [8], но в этом случае формируемые пучки практически теряют свои модовые свойства.

Обобщение ГГ мод с добавлением гауссовой составляющей рассмотрено в работе [15], где вводится понятие ГГ пучков, энергия которых ограничена. Такие пучки при распространении будут «расплываться» еще быстрее, чем чисто фазовые аналоги ГГ мод [9], но они удобны для формирования и были успешно использованы в задачах оптического микроманипулирования [16].

Амплитудная и фазовая особенности распределения ГГ мод в центре начальной плоскости (в центре перетяжки), с одной стороны, затрудняют физическую реализацию этих мод, а с другой - являются причиной неограниченного увеличения пространственной частоты [4]. Данный факт позволяет рассматривать ГГ моды в качестве аналога так называемых суперосциллирующих функций [17, 18], используемых для сверхразрешения [19].

Исследования преобразования особенностей ГГ мод при их распространении в ближней зоне (несколько длин волн) были бы полезны в решении задачи субволновой локализации светового излучения.

В работе [10] были аналитически рассмотрены непараксиальные гипергеометрические пучки, однако оценки размера центрального светового пятна сделаны только для случая отсутствия логарифмической фазовой функции. Использование же амплитудной сингулярности энергетически неэффективно.

Сравнение линейного и логарифмического акси-конов, формирующих бесселевые и ГГ моды , соот- ветственно, проводилось в работе [20], но только в параксиальной области.

В данной работе численно с использованием интеграла Релея-Зоммерфельда первого типа исследуется дифракция ограниченных ГГ мод и гипергеометрических пучков в ближней зоне дифракции (порядка нескольких длин волн). Интегральное преобразование реализовано на основе быстрого алгоритма, описанного в [21].

1. Гипергеометрические моды

Параксиальное волновое уравнение в цилиндрических координатах (уравнение типа Шредингера) имеет вид:

Обобщенные ГГ пучки, энергия которых ограничена за счет добавления гауссовой составляющей, рассмотрены в [15]. Они представляют собой трехпараметрическое семейство функций и являются обобщением гипергеометрических мод [2, 3] и двухпараметрических гипергеометрических пучков [4].

Для исследования дифракции обобщенных ГГ пучков в ближней зоне дифракции было использо-

вано следующее выражение для комплексного распределения во входной плоскости ( z = 0):

„ z ч 1 f r I m      f r ² I

E Y’ n , m ⁽ r ’ Ф ) =             exp X - I ^X

2п У w J     I 2о J

д д ² 1 д 1 д ² )

² ikS" ^{1      1}       *' Тт| E ⁽ r ’ ф ’ z ) = ⁰’     ⁽¹⁾

д z д r   r д r r дф J

I          r            1

X exp I i yln—+ inф I, У     w     J

где ( r, ф ) - поперечные полярные координаты, z - координата, направленная вдоль оптической оси, к = 2 п/% - волновое число света с длиной волны % .

В [2, 3] было показано, что уравнению (1) удовлетворяют функции, образующие ортонормированный базис:

E Y, n ^{( r} ’ Ф , z ) =

11                i Y—1

( - 1)¹ n ( 2 z ) 2

, I I —7 I X 2n | n |! ( kw ² J

X exp

iπ

^- y⁽l ⁿ\ ^- i Y⁺ 1)

f I n i + 1 - i Y

× F

^{1 1} 1           2

f kr ²

У 2 z

Γ f I n+iY+1)

I2 У

II.-, ikr ² I

|n\ +1;—— I exp( in Ф )’ 2 z

X ,(2)

J

где о - радиус перетяжки гауссова пучка, m - целое число, определяющее поведение амплитудной составляющей.

Заметим, что при о^ ^ и m = - 1 выражение (5) сводится к ГГ модам (2) в плоскости перетяжки. Если же о ^ ^ и m = 0, то амплитудная функция заменяется на постоянную величину и в плоскости перетяжки в комплексном распределении ГГ пучка остается только особенность, связанная с логарифмической фазовой функцией.

Выражение (5) рассматривалось как входная функция при численном моделировании распространения ограниченных апертурой ГГ мод и обобщенных ГГ пучков с помощью интеграла Релея-Зоммерфельда первого типа:

ik ℓ

E ⁽ u ’ v ’ ^z )     ~ IT E 0 ^{( x} ’ y ⁾-_г

2nJ£          I

где n - целое число (порядок вихревой фазовой сингулярности, топологический заряд), у - комплексное число, являющееся вторым индексом ГГ моды; w - вещественный параметр, задающий масштаб ГГ моды, аналогичен радиусу перетяжки гауссового пучка; Г( x ) - гамма функция; 1 F 1 ( a,b;x ) - вырожденная (или конфлюэнтная) гипергеометрическая функция [22]:

1 F ( a , b , x ) =

-----"b ¹----- [ f ^{- 1}(1 - 1 ) ^{b -} a ^{- 1} Г ( a ) Г ( b - a )^J₀

exp( xt )d t .

Выражение (3) может также быть записано в виде ряда Тейлора (функция Куммера):

( a ) m X m

^{( b} ) m m ^!’

∞

1 F1( a ’ b ’ x) = £ m =0

где ( a ) _m = a ( a +1)( a +2)...( a + m -1) - символ Похгамме-ра, ( a ) g =1.

В работе [5] было показано, что при расчете ГГ мод интегральное представление (3) является более устойчивым к росту значения аргумента x = ikr ²/2 z , чем полиномиальное представление (4).

где I = (j(u - x )² + ( v - y )² + z ², E ₀ ( x , y ) - входное поле (5) в декартовых координатах.

Для вычисления интеграла (6) был применен быстрый алгоритм, использующий возможность факторизации функции (5) на радиальную и угловую составляющие [5, 21]:

E Y ,n ’ m ( r , ф , z ) = G ( r , z , Y , n , m )exp( in ф ) .          (7)

• 2.    Численные эксперименты

Рассмотрим дифракцию ограниченной ГГ моды (5) при следующих параметрах: о^ ^ , w = 1, Y = -10, n = 0, m = - 1, длина волны освещающего пучка % = 633 нм, внутренний и внешний радиусы ограничивающей кольцевой диафрагмы R 1 = 0,03 % , R ₂ = 3 % , число отсчетов по радиусу равно 100 (т.е. около 30 точек на длину волны).

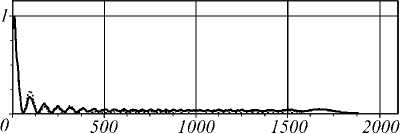
Вид амплитуды и фазы входной функции (5) при таких параметрах показан на рис. 1, на котором хорошо видно, что из-за резко спадающего амплитудного распределения формирование ГГ мод является крайне энергетически неэффективным. Поэтому в ряде работ [4, 7-9] рассматривались ГГ пучки, сформированные при замене аналитической амплитудной функции на гауссовую или постоянную.

В данной работе, наряду с ограниченной идеальной ГГ модой, рассмотрена ее чисто фазовая аппроксимация (эффективность при этом возрастает пропорционально площади оптического элемента). В этом случае в параметрах входной функции (5) вместо m = - 1 полагается m =0. На рис. 2 показаны соответствующие радиальные сечения амплитуды и фазы.

k                               I ikp2 I

E ( ρ , θ , z ) = exp( ikz ) exp( in θ ) exp        ×

iz                               I 2 z J

r                  I / кт¹

× E ( r ,0,0)exp ^ikr 2 z

r d r .

а)

Рис. 1. Амплитуда (негатив) (а) и фаза(б) ГГ моды с γ =-10, n=0, m= - 1

В табл. 1 приведены результаты численного моделирования распространения комплексных распределений, представленных на рис. 1, 2 в ближней зоне

б)

о v z‘ J V z J

Последнее преобразование является параксиальным, т.е. используется при выполнении условия па-раксиальности:

z ≫ ( u - x )² + ( v - y )² ,

и его применение в ближней зоне дифракции является некорректным. Однако выполнение преобразования (8) требует значительно меньших временных затрат, чем преобразование (6). Сравнение результатов действия этих двух операторов распространения позволяет выяснить более точную, чем (9), границу применимости интеграла (8) в рассматриваемой задаче.

Стоит отметить, что при моделировании дифракции ограниченных ГГ мод шаг дискретизации имеет решающее значение, т.к. в этом случае ам-

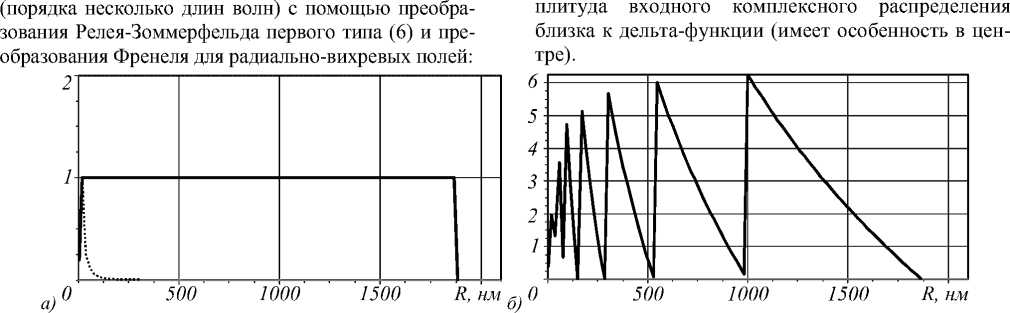
Рис. 2. Радиальное сечение ГГ моды с γ =-10: амплитуды при m= - 1 (точечная линия) и m=0 (сплошная линия)(а), а также фазы (б)

Таблица 1. Дифракция ограниченной ГГ моды (5) γ =-10, при m= - 1 и m=0 в ближней зоне при использовании непараксиального и параксиального операторов распространения

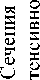
О "    500      1000      1500     2000

О 500      1000      1500     2000

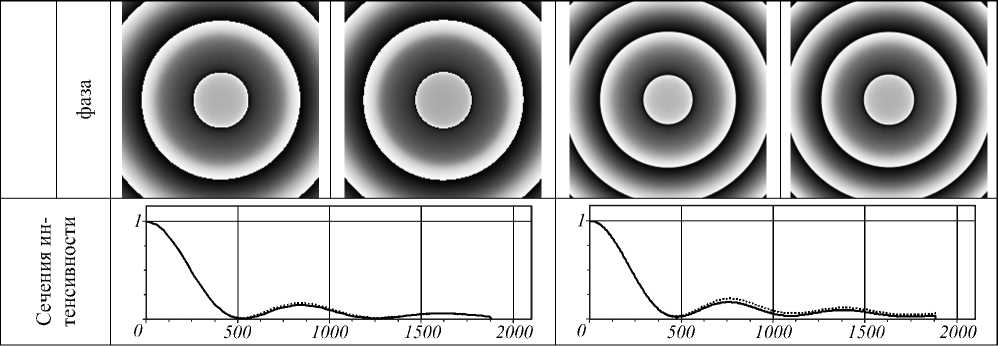
FWHM = 113 нм     FWHM = 3770 нм

FWHM = 150 нм

FWHM = 300 нм

FWHM = 76 нм      FWHM = 85 нм

FWHM = 301 нм

FWHM = 301 нм

FWHM = 151 нм

FWHM = 160 нм

	н о о m к о н к к	^i^		(5)
II		FWHM = 302 нм	FWHM = 302 нм	FWHM = 189 нм	FWHM = 170 нм
м	Cd	Ei			и
		8LJ8			^^

О        500      1000      1500     2000

FWHM = 528 нм

FWHM = 528 нм

FWHM = 470 нм     FWHM = 470 нм

К сожалению, несмотря на использование быстрого алгоритма, для выполнения преобразования (6) с высокой степенью дискретизации требуются значительные временные ресурсы (см. табл. 2).

Таблица 2. Сравнение операторов распространения по временным затратам на расчет

Число отсчетов N	Время выполнения
	Преобразование (6)	Преобразование (8)
100	4 секунды	0,5 секунды
200	79 секунд	1 секунда
400	29 минут	3 секунды
800	11 часов	20 секунд

Повышение числа отсчетов при использовании преобразования (8) на несколько порядков меньше сказывается на временных затратах, но значительно улучшает визуальную картину и позволяет получить приемлемые результаты (с погрешностью порядка 10%) значительно раньше, чем предполагается выполнение условия параксиальности (9) (при этом расстояние от входной плоскости должно быть значительно больше 8 λ ).

• 3.    Анализ результатов

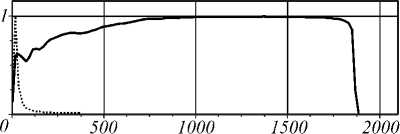
Как видно из табл. 1, уже на расстоянии в половину длины волны картины дифракции при использовании непараксиальной модели для аналитической ограниченной ГГ моды и ГГ пучка, который фактически является ее фазовой аппроксимацией, очень близки. При дальнейшем увеличении расстояния различие между ними становится все меньше и на расстоянии в пять длин волн они полностью совпадают.

Размер центрального светового пятна по полуспаду на расстоянии z = 1 λ (FWHM = 300 нм ≈ 0,47 λ ) оказывается меньшим, чем дифракционный предел, равный в воздухе половине длины волны.

Таким образом, в рамках скалярной непараксиальной теории численно показана возможность преодоления дифракционного предела с помощью дифракционного фазового логарифмического аксикона.

Хотя на расстоянии в несколько длин волн применение интегрального преобразования Релея-

Зоммерфельда считается вполне корректным [23, 24], полученные результаты тр ебуют дополнительной проверки с использованием более строгой теории.

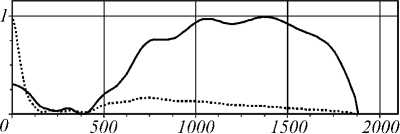
Интересно также отметить, что на расстоянии z = 5 λ применение параксиального оператора распространения дает очень близкий результат, хотя условие параксиальности еще не вступает в силу, а числовая апертура рассмотренных дифракционных оптических элементов достаточно велика NA ≈ sin ( arctg( R / z ) ) = 0,5 и соответствует примерно 30 ° для периферийных лучей.

Объяснить данный факт можно специфическим распределением входной функции. При зависимости амплитудной функции 1/ r вклад в картину дифракции даже на очень малых расстояниях вносит только центральная зона входного поля, что соответствует низкому значению числовой апертуры.

Для постоянной амплитуды ситуация несколько сложнее. Фазовую функцию на рис. 2 б можно приближенно представить как набор линейных аксико-нов exp( i α r ) с переменным параметром α .

На рис. 3 показан вид логарифмической функции (смещенной вверх) с γ = - 10 для нормированного отрезка оси абсцисс, из которого наглядно видно, что данную функцию можно условно разбить на несколько зон:

Q exP(ia ln r) = £ gq (r), (10) q=1

exp( i α _qr ), r ∈ [ r_{q - 1}, r_q ]

0, else , где gq(r) =

соответствующих области кольцевого диафрагмирования (или аппроксимации значением в ближайшем дискретном отсчете), области высоких и средних частот (порождающих затухающие волны в ближней зоне дифракции), а также область, связанную с распространяющимися волнами. Последняя может быть разделена на две части: причем та часть, где значение фазовой функции меньше 2 π (ниже сплошной линии), не участвует в формировании бездифракционных пучков [20].

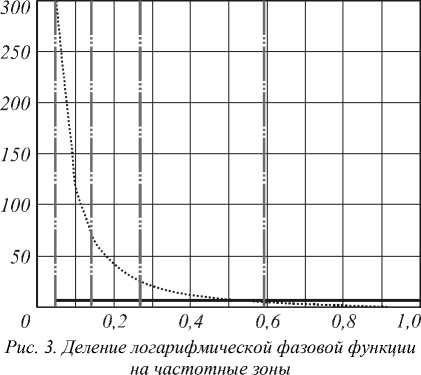
Таким образом, в формировании распространяющихся волн, имеющих бездифракционные свойства, участвует только средняя часть дифракционного логарифмического аксикона, а, следовательно, условие параксиальности удовлетворяется значительно раньше, чем можно ожидать, учитывая полный размер входной апертуры.

Оценить параметр линейного аксикона в каждой точке логарифмического аксикона можно по следующей формуле:

ln r

α(r) = γ , (11) r используя которую легко оценить переменную числовую апертуру [20]:

NA ( r ) = α ( r ) λ /2 π .

На рис. 4 показан график α(r) для логарифмиче- ского аксикона с γ = -10. На рис. 5 приведены соответствующие значения числовой апертуры для периферийной части. Известно, что для дифракционного линейного аксикона числовая апертура определяется не по отношению поперечного радиуса оптического элемента к продольному расстоянию, а по периоду кольцевой решетки. В данном случае распространяющиеся в свободном пространстве волны будет формировать только периферийная часть, имеющая числовую апертуру меньше единицы.

Как видно из рис. 5, в периферийной части логарифмический аксикон можно аппроксимировать кусочно-линейной функцией со средней числовой апертурой на каждом отрезке:

NA = ^

0,9, r e [1200нм,1300нм] 0,8, r e [1300нм,1500нм]

0,7, r ∈ [1500нм,1800нм]

0,6, r >  1800нм

В этом случае в параксиальной модели можно считать, что каждое фазовое кольцо формирует поперечную интенсивность, пропорциональную квадрату функции Бесселя нулевого порядка [25]: J ₀²( k ⋅ NA ⋅ ρ )

на расстоянии до z _max ≈ r NA . Радиус центрального светового пятна такого распределения оценивается как ρ ₀ ≈ 0, 38 λ NA и примерно равен FWHM.

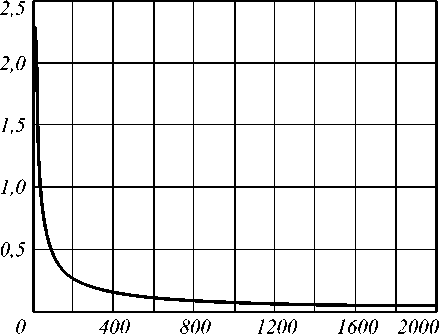
Рис. 4. Переменный параметр линейного аксикона (8) для фазовой функции ГГ моды γ =-10, m=0

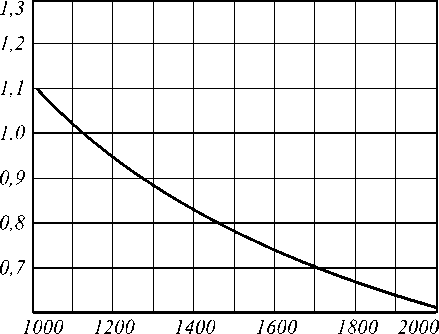
Рис. 5. Переменная числовая апертура в периферийной части, соответствующая фазовой функции

ГГ моды γ = -10, m = 0

Используя (13), можно определить, что кольцо, вносящее основной вклад на расстоянии около 1 мкм, будет формировать световое пятно диаметром (до нулевых значений интенсивности) около 200 нм. Далее пятно будет уширяться, и на расстоянии 5 мкм от входной плоскости будет работать только самое крайнее фазовое кольцо с NA = 0,6, формируя световое пятно с FWHM = 400 нм.

Эти цифры вполне согласуются с результатами, получаемыми с помощью параксиального оператора. Однако непараксиальная модель предсказывает, что размеры центрального светового пятна будут несколько больше. На меньших расстояниях, т.е. при более сильном нарушении условия параксиальности рассогласование соответствующих результатов для преобразований (6) и (8) становится значительным.

Заключение

Амплитудная и фазовая особенности распределения ГГ мод в центре начальной плоскости, с одной стороны, затрудняют физическую реализацию этих мод, а с другой - являются причиной неограниченного увеличения пространственной частоты.

В данной работе в рамках скалярной непараксиальной теории дифракции численно проведены исследования преобразования особенностей ГГ мод при их распространении в ближней зоне (несколько длин волн) и показана возможность субволновой локализации светового излучения (FWHM 300 нм ≈ 0,47 λ ) на расстояниях, превышающих длину волны, т.е. в области распространяющихся волн.

Важно, что такой эффект можно получить с помощью чисто фазового дифракционного логарифмического аксикона, т.е. без использования амплитудной сингулярности, приводящей к большим потерям энергии.

Также в ходе вычислительного эксперимента обнаружено, что параксиальный интегральный оператор позволяет получать корректные результаты значительно раньше, чем предсказывает условие пара-ксиальности. Данный факт объяснен на основе представления фазовой функции логарифмического акси-кона как набора линейных кольцевых аксиконов.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF PG08-014-1), гранта Президента РФ поддержки ведущих научных школ (НШ-3086.2008.9) и гранта РФФИ 08-07-99007.