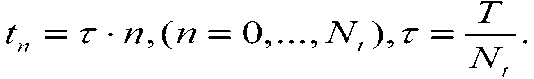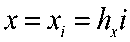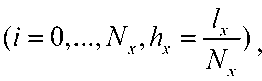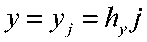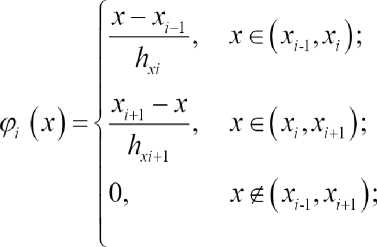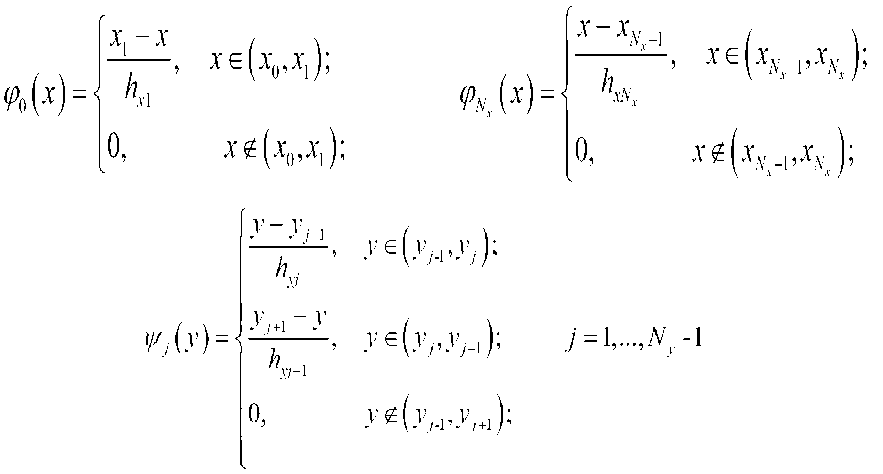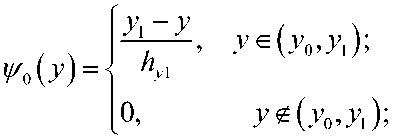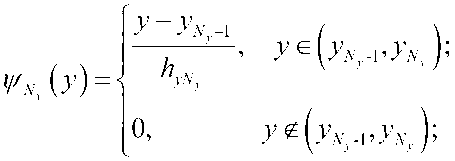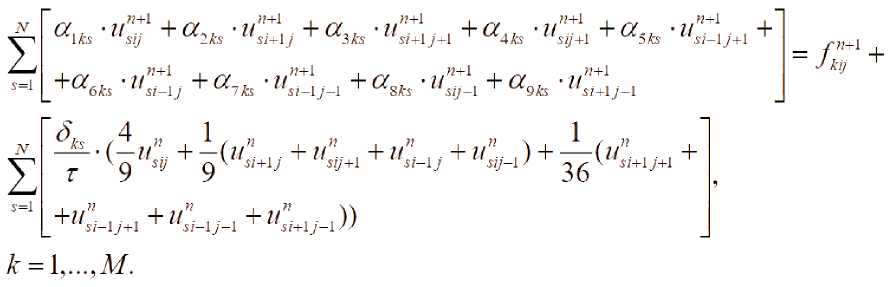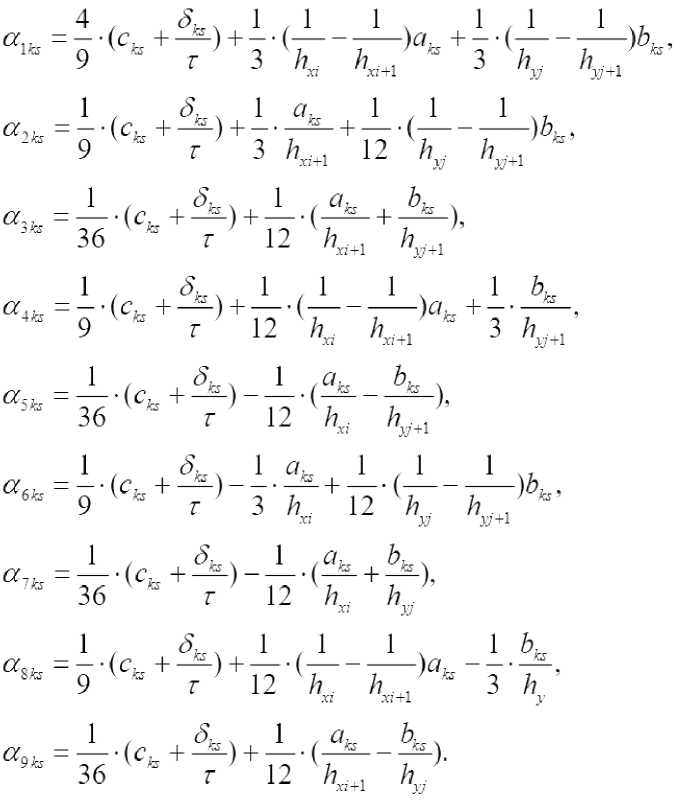Гиподинамия и роль физической активности в сохранении здоровья студентов

Постановка смешанной задачи: Пусть.

В области G := {(t,x,y):tE (0,T), (x,y) e □} найти вектор- функцию и удовлетворяющей системе dU(x,y.t) + AdU(.x,y,t) + BdU(x,y,t) + Cu(x y t) = F(x y 0

dt           dxdy с граничным

(D-N-)u\sa=O(2)

и начальным

n(O,x,y) = no(x,y);(3)

условиями.

Здесь A,В симметрические, постоянные матрицы размерностью MxM , В постоянная матрица размерностью MxM ,

U(t, X, V) = (w, ( / ,Л'- V), U2

В<Ух,у) = ( f^x,y\ f₂(t,x,y\..., f_M^     ,

/^,х,_У)еС^_т), / = ЦЙ^,

2/o (^ y) = Ooi О’ УУ-Z/O2 (^’ УУ-■ - •’ 2/o^ O’ y)> заданная вектор функция u^A^^c^^ i = l,M .           , ” =

• 2.    Построение разностной схемы.

  Отрезок \0J] разобъем на ^i частей

  
  
  

  Проведем прямые

  
  
  
  
  
  
  
  
  

(У             N ). Пересечение прямых x = Xj иу = у J , называемый узлом сетки, обозначим через              .

Сетка разбивает прямоугольный область Q на части (элементы). Каждый элемент прямоугольник. Элементы, один из вершин которых, является узел Мд называются элементами этого узла. Объединение этих узлов обозначим через .

Будем искать приближенное решение ^и^п^У) на каждом слое t по времени в виде

^ = “Л^а’) = ЕЕмо ■ Q^y},             (4)

где (У(х,у) базисные функции,

11у=И^^УуА^={ Щу (tn ), П.у (t„ ),..., II My (t„ ) )Г = ( Щу ,ll2y,-,ll’^ ■

Аппроксимируем систему (1) в узле My т.е. в системе (1)

du производную по времени аппроксимируем отношением ot

u(t + T,X,y}-u(t,X,y}           /     \                /      \

, вместо U[t,X, V) подставим "At^y) , каждое T уравнение полученной системы умножим на Qy^.y} и проинтегрируем по

^ij . В итоге получим неявную разностную схему:

(iCM +T         +т\вУ^Оу +r(C<¹,al

= r(Fr\Q_u)_n + ^,Q,)_n (w,)eQ„.

где                                 .

В качестве примера базисной функции берем следующие функции Qi^y^fiM-ysM, где

тогда после некоторых несложных вычислений из (5), разностную схему системы (1) в узле

:

получим следующую

М..=М(х.-,у^С1_и,

Здесь ^ks

1 если к = s

О если кФ s

Для того чтобы замкнуть систему линейных алгебраических уравнений(СЛАУ) (6) воспользуемся аппроксимациями граничных и начальных условий:

(D-^MZW+I,x,j/P|^

(D-N)u(t_n+ly^^ =0

(D-N^t^x^y)_v4 =0

при :

i/^O^^y^i/^x^y^, M^y^Qh.                 (8)

В качестве дополнительных граничных условий (неопределенных дифференциальной постановкой смешанной задачи) используется аппроксимация исходной системы. В итоге получим замкнутую систему линейных алгебраических уравнений. СЛАУ решим методом главных элементов.

Нерегулярная сетка создается следующим образом. Область Q разбиваем выше указанным способом на несколько частей. Это является первоначальной “грубой” сеткой. На этой сетке находим численное решение задачи (1)-(3). После нахождения решения, если модул разности значений , хотя бы одной компоненты вектор-функции щм , в узлах между Му , м или в узлах между м,м больше заданного число ^ > о , то середину этих узлов ставим новый узел. Создаем первую нерегулярную сетку. На этой сетке повторна находим численное решение задачи (1)-(3) Аналогично выше указанным способом создаем следующую нерегулярную сетку. Этот процесс будем повторять пока не будет выпольнятся неравенства UkMj~Ukij “^ и .

• 3.    Численные расчеты.

В качестве примера рассмотрим задачу 1.

Пусть Q = {(x, v): 0 < x < 2^,0 < у < 2^].

Возмем fl — 1 и (p = л/2 sinxsinj^cos V2/ начальные условии при / = 0

Uy = 0,u₂ = O,w₃ — д/2 sin A'sin j^

условие на границе

Из этого следует, что на всей стороне прямоугольника

.

При t >0 точное решение смешанной задачи будет ip = cos x sin у sin V2/, u2 = sin x cos v sin ^[2t, гу = л/2 sinx sin i’ cos V2/1 .

В таблице ниже приведены значения разницы II^й-4_(n) на неравномерной сетке при различных разбиениях по времени t и первоначальном разбиении N_x=XN_y=3 по X и по у соответственно, при ^ = 0,2 и при .