Гипотеза о крупном планетном теле на периферии солнечной системы
Автор: Гулиев А.С. , Гулиев Р.А.
Журнал: Вестник Международной академии наук (Русская секция) @vestnik-rsias
Рубрика: Физико-технические, химические, точные науки
Статья в выпуске: 1, 2018 года.
Бесплатный доступ
Рассматриваются отдельные аспекты гипотезы Гулиева о возможности существования крупного планетного тела на расстоянии 250-400 а.е. и его трансфера наблюдаемых комет. В этой гипотезе основной акцент делается на закономер ности в движении комет, приходящих с далеких областей солнечной системы. В настоящей работе анализ охватывает 1249 комет, наблюдавшихся до 2017 года. Показано, что существует плоскость вблизи которой имеет место концентра ция кометных перигелиев. Она имеет параметры Ip=86°.2; Ωp=271°.7 и согласно гипотезы, является следствием действия крупного планетного тела на расстоянии 250-400 а.е. В этом интервале количество афелиев и далеких узлов кометных орбит заметно (в пределах статистических достоверностей) превышает ожидаемый фон. На базе собранного кометно го материала оценены элементы предполагаемого планетного тела: а=337 a.e.; e=0.14; ω=57°; Ω=272°.7; I=86°.
Кометы, планета х, трансфер
Короткий адрес: https://sciup.org/143162086
IDR: 143162086
Текст научной статьи Гипотеза о крупном планетном теле на периферии солнечной системы
В настоящее время в астрономической литературе активно дискутируется вопрос о существовании крупного планетного тела на периферии солнечной системы. По мнению некоторых специалистов [8, 9] масса такого тела может составлять до десяти массы Земли. Основной предпосылкой для такой гипотезы является некоторая специфика недавно найденных транснепту-новых или койперовых тел. Однако есть также специалисты, которые в этом вопросе исходят из закономерностей, присущих долгопериодическим кометам. В частности один из авторов настоящей статьи в работах [5], посвященных проблеме неизвестных планет считает, что в распределении перигелиев и далеких узлов орбит долгопериодических комет заметна роль или влияние далеких неизвестных планет.
Исследование распределения перигелиев комет имеет давнюю историю. Исторические обзоры по этому вопросу содержатся в работах Литлтона [11], Всех- святского [2], Радзиевского [8], Гулиева [3], Yabushita [14] и других авторов. В частности, установлено, что концентрация кометных перигелиев вблизи эклиптики присуща только периодическим кометам. У долгопериодических комет однозначной концентрации в той зоне специалистами не замечена. Поиску возможной точки концентрации перигелиев на небесной сфере посвящена работа Натансона [13]. Перечисленные вопросы и некоторые новые подходы в данном вопросе станут объектами исследования настоящей работы, построенной на основе новейших данных.
Использованный материал
Настоящее исследование охватывает кометы, имеющие следующие характеристики:
-
• Комет, обнаруженные до начала 2017 г.;
-
• кометы, имеющие перигелийные расстояния больше 0.1а.е. (следовательно, коротко-перигелийные кометы не рассматриваются);
-
• кометы, имеющие афелийные расстояния больше 30 а.е., т.е. больше расстояния Нептуна;
-
• если комета распалась, то в списке фигурируют только данные более крупного фрагмента ее ядра с обозначением А.
Составленная таким образом, наша базисная таблица содержит данные 1249 комет. Она начинается с кометы 1P/-239 K1 и заканчивается объектом C/2016 X1. При подборе данных использованы данные каталога Марсден и Вильямс [12] и отдельных номеров Minor Planet Electronic Circulars (MPEC) Международного Астрономического за период 2008—2016.
Алгоритмы вычислений
Предположим мы ищем плоскости (большой круг небесной сферы), вблизи которой имеет место концентрация кометных перигелиев. Положение такой плоскости определяется способом, описанном в работе Гулиева и Дадашова [7]. Вначале находятся направляющие косинусы радиуса-вектора каждой точки перигелия в прямоугольной эклиптической системе координат. Далее находятся эмпирические выражения трех плоскостей относительно которых точки имеют минимальную дисперсию. Они находятся в виде:
Z = ax+by; Y=az+bx; X=bz+ay
Для облегчения задачи второе и третье выражения также выражаются через Z поскольку он означает отклонение от эклиптики. На следующем этапе предпочтение дается эмпирическому выражению, дающему минимальную сумму Z2 , которую будем обозначать через S . Найденная плоскость будет определяться двумя координатами: Ω p — долготой восходящего узла соответствующего большого круга небесной сферы и Ip — наклоном этого круга к эклиптике.
В случае, если нет доступа к прикладным программам, в расчетах можно применять оператор ЛИНЕЙНЫЙ из программной среды EXCEL. Он дает не только искомые коэффициенты, но также их погрешности, уровень детерминированности полученного эмпирического выражения и остаточную дисперсию S, что особенно важно для сравнительного анализа в случае различных плоскостей.
Результаты расчетов
Применение вышеописанного алгоритма к базисной таблице показывает существование следующей плоскости, вблизи которой имеет место перигелиев
Ip=86°.18; Ωp=271°.74 (S=368.18) (1)
Для краткости в дальнейшем найденную таким образом плоскость будем называть оптимальной плоскостью. Заметим, что она не совпадает с плоскостью Галактики:
Ip = 60°.2; Ωp=269°.3.
Использованная методика позволяет определить возможности погрешности для параметров Ω p и IP . С их учетом можно утверждать, что параметры плоскости (1) имеют следующие доверительные интервалы:
270°.3<Ωp<272°.8; 84°.4< IP <87°.7
Для того, чтобы разобраться в причинах существования плоскости (1), было решено в отдельности анализировать распределение перигелиев относительно различных кометных групп:
-
• Кометы с е отличных от 1 (N=825);
-
• Кометы с известными «первоначальными» орбитами (N=499); (источник: Marsden, Williams, 2008);
-
• Кометы с перигелийными расстояниями больше 7 а.е. (N=30); 6 а.е. (N=63); 5 а.е. (N=117); 4 а.е. (N=180); 3 а.е. (N=288); 2 а.е. (N=462); 1 а.е. (N=798) и меньше 1 а.е. (N=441);
-
• Кометы, открытые до 1750 г. (N=101); 1800 г. (N=138); 1850 г. (N=197); 1900 г. (N=327); 1950 г. (N=452), 2000 г. (N=738);
-
• Кометы с афелийными расстояниями меньше 6 а.е. (N=297); от 30 до 250 (N=170), от 30 до 200 а.е., от 30 до 150 а.е., от 30 до 100 а.е., больше 1000 а.е., исключая гиперболических (N=638). «Гиперболические» кометы не входят в нашу выборку, они служат только для сравнения.
-
• 3 группы комет, имеющие абсолютный блеск в следующих интервалах: слабее 9m; от 6m до 9m; ярче 6m. В качестве источника использованы данные каталога Всехсвятского [7] его дополнений: N=99, 198 и 220, соответственно
-
• Кометы, имеющие оскулирующие гиперболические е (N=296),
-
• Кометы с некоторыми другими характеристиками.
Параметры оптимальных плоскостей для этих кометных групп приводятся в таблице. Из таблицы видно, что эти плоскости мало отличаются от (1).
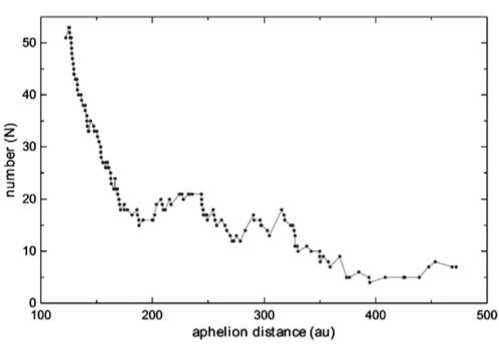
Впервые попытка интерпретации существования плоскости (1) сделана в работе Гулиева [4]. В работе было установлено, что в интервале 250—400 а.е. вблизи той плоскости число далеких узлов орбит ДПК имеет «фоновое» увеличение. Из этого обнаруженного факта выдвинута гипотеза о возможном существовании крупного ТНО — источника комет в зоне (250 Возьмем с нашего списка 150 кометы, имеющие Q от 100 до 475 а.е. и проведем их одномерный анализ по шкале расстояний. Для этого с помощью метода Стерджеса из математической статистики [10] определим длину оптимального интервала, равную 47.8 а.е. До- Признак выделения группы, наклон, восходящий узел оптимальных плоскостей, вблизи которых перигелии комет имеют концентрацию, количество комет и остаточная дисперсия Признак группы Ip Q p Кол-во N S Признак группы Ip p Кол-во N S Все 1249 кометы 86.14 271.85 1249 370.17 Кометы до 1950 86.02 272.34 457 134.69 q >7 а.е. 82.6 266.77 30 10.98 Кометы до 2000 85.30 272.53 740 216.67 q>6 а.е. 84.17 272.23 62 20.3 Q>250 а.е. 87.73 272.3 1082 310.10 q>5 а.е. 84.53 271.53 117 34.15 Q>1000 а.е. 84.81 271.47 638 180.94 q>4 а.е. 86.69 271.71 178 54.76 e>1 88.80 272.06 296 88.81 q>3 а.е. 88.76 269.75 287 87.52 H<9m 80.83 273.44 99 27.04 q>2 89.25 270.34 461 137.87 H от 6m до 9m 88.75 276.24 198 59.15 q>1 85.9 271.64 803 239.75 H<6m 84.04 276.24 220 57.71 q<1 85.84 272.01 446 127.41 Q от 30 до 250 а.е. 88.02 276.24 170 59.54 Кометы до 1750 87.24 276.4 101 29.93 Q от 282 до 400 а.е. 81.01 274.93 46 12.29 Кометы до 1800 86.68 274.25 138 40.41 Orig. 1/a 88.56 271.4 499 140.10 Кометы до 1850 85.37 271.4 197 58.24 Q<6 а.е. 68.98 270.31 297 136.02 Кометы до 1900 86.02 270.68 327 94.05 100 200 300 400 500 aphelion distance (au) Рис. 1. Численность Q в перекрывающихся интервалах длиной 48 а.е. для афелиев комет. Рис. 2. Численность далеких узлов долгопериодических комет относительно плоскости (1) в перекрывающихся интервалах длиной 40 а.е. бавляя каждый раз эту величину на Qi легко можно определить 150 интервалов и подсчитать значение афелиев (N) в каждом из них. Другими словами, в статистике афелиев комет можно применять методику переплетенных интервалов. Полученная картина (рис. 1) явно указывает на отклонение в интервале 250—400 а.е. от ожидаемого распределения типа 1/Q. Это может служить еще одним косвенным доказательством того, что указанная зона каким-то образом имеет отношение к процессу пополнения наблюдаемых ДПК. Подобная, но менее значимая картина наблюдается также и в распределении далеких узлов относительно плоскости (1). Оно отражено на рис. 2. Здесь также использованы данные по переплетенным интервалам длиной 40 а.е. На общем фоне наибольшее отклонение наблюдается в интервале 278.2—318.2 а.е., где количество узлов составляет 19. Однако главный аргумент гипотезы Гулиева связан с распределением расстояний дальних узлов орбит ДПК. В работе [4] продемонстрирована их перенаселенность т.е. избыточность относительного некоторого фона в интервале 250—400 а.е. Напомним, что для определения такого фона используется данные по узлам относительно 67 зон. В настоящей работе количество таких зон увеличено до 229, а количество комет почти в полтора раза (1249 против 859) превышает численность комет, использованной в цитируемой работе. На основе расчетов относительно плоскости (1) мы получили следующие дисперсионные величины (их описание приведено в цитируемом источнике): N=43, –n=27.51, σ=6.34, t=2.44, α>0.99. Меняя границы применяемого интервала можно найти более эффективного значения параметра t. Например, для интервала 283 — 357 а.е. он оказывается равным 3.12, что фактически исключает фактор случайности. Гипотеза Гулиева предсказывает важную закономерность, которую можно проверять на базе нашего списка комет. Она допускает, что гипотетическая планета движется не только под большим углом, но и имеет значительный эксцентриситет орбиты. Следовательно, если по точкам дальних узлов орбит соответствующих комет провести эллипс с наименьшей дисперсией и по афелиям в интервале 250—400 а.е. провести второй эллипс (также с наименьшей дисперсией), направления больших полуосей этих двух эллипсов либо должны совпадать, либо отклоняться друг от друга минимально. Для проверки вышеприведенного последствия гипотезы мы отобрали 9 комет, имеющих широты линии апсид к плоскости (1) в пределах ±5°. Расчеты показывают, что значения Q соответствующих комет находятся в интервале 286—388 а.е. Если полагать, что и планета движется в этом интервале, то ее 4 оценочные элементы (большая полуось, эксцентриситет, и два угловые) будут: а=337 a.e.; e=0.136; Ω=271°.74; I=86°.18 Далее пренебрегая значений B' и задавая различные ω можно найти оптимальный эллипс, относительно которого точки афелиев имеют наименьшую дисперсию. Такое значение окажется равным 45°. Аналогичную задачу можно решать относительно комет, дальние узлы которых относительно плоскости (1) находятся в пределах 286—388 а.е. Количество таковых оказалось 25. Моделирование параметра ωпредполагаемой планеты показывает, что минимальное суммарное невязки достигаются при значении 70°. Это означает, что угол между большими полуосями двух оценочных орбит составляет 25°. Кстати, в работе [6] такое тестирование для узлов и афелиев периодических комет с целью «определить» направление линии апсид Юпитера дало значение, отличающееся от истинного всего лишь на 10°. Учитывая точность кометных орбит, ограниченность их количества можно констатировать, что согласие между двумя значениями ω является удовлетворительным для гипотезы. Следовательно, если усреднять параметры, то можно полагать, что гипотетическая планета имеет следующие ориентировочные элементы орбиты а=337 a.e.; e=0.14; ω=57°; Ω=272°.7; I=86°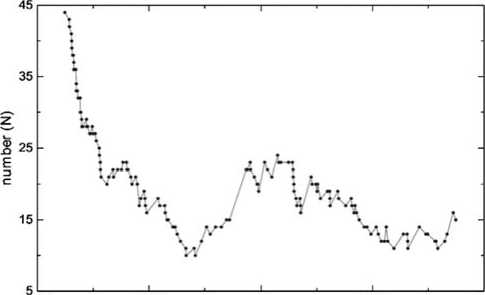
Список литературы Гипотеза о крупном планетном теле на периферии солнечной системы
- Всехсвятский С. К. Природа и происхождение комет и метеорного вещества. М. Просвещение. 1966: 186.
- Гулиев А. С. О возможности существовании двух трансплутоновых планет Письма в АЖ. 1992; 18 (2): 182-188.
- Гулиев А.С. Результаты исследования узловых расстояний долгопериодичес ких комет. Кинематика и физика небесн.тел.1999. 15 (1): 85-92.
- Гулиев А.С. О связи долгопериодических комет с известными и неизвестны ми планетами. Письма в АЖ. 2007. 33 (7): 631-640.
- Гулиев А. С., Гулиев А. С. К одной гипотезе о неизвестной планете. Астроно мический Журнал Азербайджана, 2012; 7 (3): 5-13.
- Гулиев А. С., Дадашов А. С. О трансплутоновых кометных семействах. Астрон. вестник. 1989: 23 (1): 88-95.
- Batygin K., Brown M. E. Evidence for a Distant Giant Planet in the Solar System. Astronomical Journal. 2016; 151 (2): 22-33.
- Gmurman V.E. Fundamentals of Probability Theory and Mathematical Statistics American Elsevier Publishing Co. 1968: 249.
- Marsden B.G., Williams G.V. Catalogue of Cometary Orbits. 17th edition. Cambridge. SAO. 2008: 207.


