Гистограммный иерархический алгоритм и понижение размерности пространства спектральных признаков

Таким образом, границы кластеров находятся автоматически и лежат в долинах многомерной гистограммы, т.е. в областях низкой плотности векторов. Важно, чтобы гистограмма и различные вектора были записаны в виде списка, определенным образом упорядоченного так, чтобы соседние векторы оказывались в непосредственной близости друг от друга, и это обеспечивает автоматизм и быстроту их нахождения. В качестве соседства данного вектора отыскивается система векторов, отстоящих от него не далее чем на единицу по каждому спектральному направлению. В первоначальном виде алгоритм был реализован на машине БЭСМ-6 автором этой статьи [5], затем перенесен на ПК [6].

Иерархиченский кластерный алгоритм

Ценность алгоритма Нарендры в том, что он не требует задания a priory никаких параметров, формы и числа кластеров. Кроме того, он быстрый, т.е. линейно зависит от числа различных векторов. Остается лишь детальность кластеризации. Во времена Нарендры компьютеры обладали небольшой памятью и быстродействием. Поэтому даже гистограмма лишь присутствующих векторов могла не помещаться в оперативную память. Тогда в каждом байте, соответствующем определенному спектральному направлению (каналу) отсекались младшие (шумовые) биты. Тем самым осуществлялось квантование векторного пространства (каждое отсечение вдвое уменьшало число уровней квантования). Детальность кластеризации также, естественно, понижалась. Однако, отсекая разное число битов, мы получаем разные системы векторов и кластеров. С усовершенствованием компьютеров мы можем уже не отсекать биты, но тогда получается очень много векторов и очень много локальных максимумов. Можно ли рассматривать их не все? Помощь приходит, если привлечь разделимость кластеров. Большинство кластерных алгоритмов не гарантируют хорошую разделимость кластеров, а между тем качество кластеризации определяется именно ей [7].

Алгоритм [1] предлагает автоматизировать выбор детальности, основываясь на минимизации разделимости кластеров. В качестве мер разделимости выступают: мера отделимости для отдельного унимодального кластера m ( n ) (1) и мера качества распределения в целом m ( n ) по K ⁽ n ) кластерам (2) .

т» =  -- ^—V^h^n),                        (1)

B^J(n) х H^n)^ = ¹

m(n) =    ^ ilUm,                                             (2)

K(n) j где hi (n) - значение гистограммы в i-той точке границы кластера j; B(n) - число точек границы кластера; H(n) - максимальное значение гистограммы; n - число квантовых уровней [8].

Минимумы меры (2) соответствуют лучшим распределениям с наиболее разделенными кластерами в среднем. Всегда mj(n) < 1 и m(n) < 1. Ценность этих мер в том, что они позволяют сравнивать распределения с тесно расположенными унимодальными кластерами, когда на их границах много общих векторов. Эти меры удовлетворяют условиям мер разделимости [7]: значения их убывает с увеличением расстояния между кластерами и ростом компактности кластеров (в смысле близости векторов кластера к модальному вектору). Кроме того, эти меры легко вычисляются, так как сравнивают скалярные значения гистограммы в центре и на – 716 – границах кластеров. Границы кластеров легко найти, используя списки соседей векторов, построенных как составная часть алгоритма Нарендры.

Алгоритм [1] представляет данные в их иерархической вложенности, последовательно увеличивая детальность рассмотрения. Сначала определяется минимум меры разделимости (2) и соответствующее число уровней квантования п. Затем для каждого полученного кластера, начиная с увеличенного п, снова находится минимум и подкластеры, ему соответствующие. Затем оценивается отделимость каждого подкластера. Данные подкластеров, для которых отделимость (1) больше d, объединяются для дальнейшего деления. Здесь не происходит остановки, потому что на более детальном уровне (большем этапе иерархии) эти данные могут удовлетворительно разделиться. Задаваемым параметром кластеризации является отделимость каждого полученного кластера d (одно для всех). Иерархический процесс деления кластеров заканчивается тогда, когда достигается максимальное значение признака по каждому спектральному каналу (обычно 255), либо по заданному числу иерархических этапов, либо из каких-то других физических соображений. Затем автоматически анализируются полученные результаты и производится возврат к тем детальностям, на которых отделимость кластера была не больше d. Кластеры, не удовлетворяющие этому условию ни на каком этапе, объединяются в один ложный кластер. Заметим, что для рассматриваемых данных тенденция такова, что с ростом детальности средняя разделимость кластеров уменьшается, соответственно (2) увеличивается. После кластеризации осуществляется глобальная сегментация изображения. В результате работы алгоритма [1] получаем существенно меньше кластеров, чем прямым алгоритмом Нарендры за счет того, что выбираем детальность рассмотрения области данных так, чтобы не нарушалось условие отделимости. Отделимость всех полученных унимодальных кластеров меньше заданного d. В то же время сохраняются достоинства алгоритма Нарендры: независимость от формы и задания числа кластеров, быстрота.

Выбор размерности данных

В данной статье предлагается учитывать не только то, что детальность в разных областях данных различна, но и то, что размерность данных в кластерах различна. Квантование пространства признаков может производиться по разным правилам. У Нарендры оно достигалось отсечением младших битов в каждом спектральном канале. Каждое отсечение уменьшает число уровней квантования вдвое. В работе [9] был предложен другой способ, более плавный, но по-прежнему в каждом спектральном направлении число уровней квантования сохранялось одинаковым. Однако в общем случае данные вытянуты вдоль какого-то направления, и правило квантования, обеспечивающее наименьшую потерю информации, требует различного подхода в различных направлениях, а именно: квантование должно сохранять ячейку квантования в форме гиперкуба (а не гиперпараллелепипеда). Это условие будет выполнено, если

^Ne 1 ₌ ^Ne2

^Se 1     ^Se 2

N

ek

Sek

где Neb Ne2, ..., Nek - числа уровней квантования вдоль для соответствующих собственных век торов по к - ортонормированным осям собственного пространства, а S2eb S2e2, ..., S2ek - соб-ee    e ственные числа.

Зададим максимальное число уровней квантования в собственном пространстве равным N em =255, таково обычное число уровней серого для данных дистанционного зондирования по каждому измерению. Тогда в соответствии с пропорциями (1) может быть найдено число уровней квантования и по другим осям собственного пространства. Для задач кластеризации это число должно быть больше или равно 2, иначе эта компонента одинакова для всех векторов и никакой роли в кластеризации не играет. Таким образом, если отношение S em / S ex < 2, то соответствующая ось x ортонормированного собственного пространства может не рассматриваться, и мы получаем сокращение размерности пространства признаков.

Ранее [9] было предложено сокращать размерность перед использованием алгоритма кластеризации. Пример: на рис. 1 представлено изображение (2772*1995) района Улан-Удэ с целью выделения области загрязнения территории. Это семиспектральное изображение Бурятии со спутника «Landsat-8», район Улан-Удэ. Исходный файл предоставлен Сибирским центром ФГПУ НИЦ «ПЛАНЕТА». Построение ковариационной матрицы спектральных данных для всего изображения и ее диагонализация методом Якоби [10] показало, что можно рассматривать три измерения без существенной потери информации (рис. 2). Сокращение размерности приводит к экономии компьютерного времени.

Также алгоритм применялся для картирования загрязнения отходами производств Омской области (рис. 3) по восьми спектральным каналам ИСЗ «Landsat-8” (3161*2590) от 08.02.2014 (разрешение 15 м).

Сокращение размерности производилось до кластеризации, анализ ковариационной матрицы данных позволил уменьшить число спектральных каналов с 8 до 3. Для 10 этапов иерархии получено 27 унимодальных кластеров. Углы розового и фиолетового кластеров на северо-востоке соответствуют загрязнению снега территории Омской области в соответствии

Рис. 1. Cемиспектральное изображение со спутника «Landsat-8», район Улан-Удэ

Fig. 1. The semispectral image from the satellite “Landsat-8”, the area of Ulan-Ude

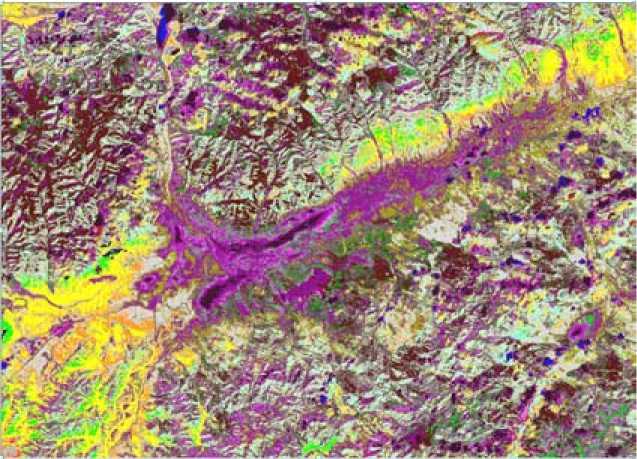
Рис. 2. Кластерная карта, полученная делимым иерархическим гистограммным алгоритмом. 15 этапов иерархии. d = 0,015. 54 кластера (включая маленькие вплоть до 1 пикселя). Загрязнение: лиловые и темнозеленые оттенки

Fig. 2. The cluster map obtained divisible hierarchical histogram algorithm. 15 stages of the hierarchy. d= 0, 015. 54 cluster (including small up to 1 pixel). Pollution: purple and dark green shades

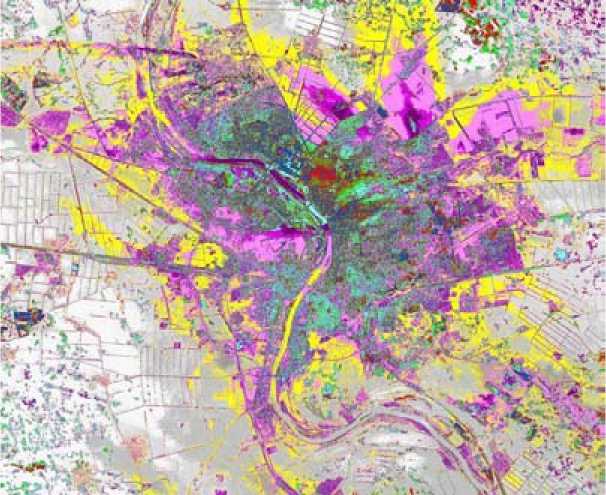
Рис. 3. Кластерная карта Омской области

Fig 3. Cluster map of Omsk region

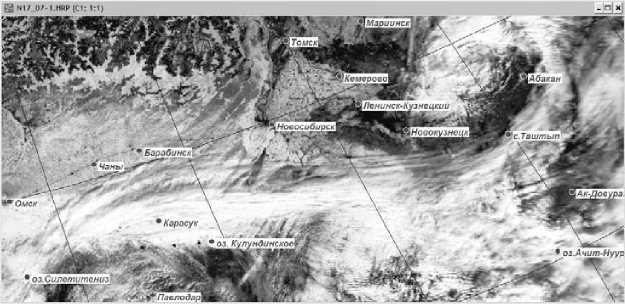
Рис. 4. Исходное изображение в видимой части спектра

Fig. 4. The original image in the visible spectrum

Рис. 5. Кластеризация иерархическим гистограммным алгоритмом с поиском размерности по кластерам; 7 этапов иерархии; задано d =0,12; получено 29 кластеров

Fig. 5. The hierarchical clustering of histogram algorithm finding the dimension of the clusters; 7 stages of the hierarchy; set d=0,12; received 29 clusters с преобладанием юго-западных ветров в области. Предельная отделимость кластеров задана d=0,15.

Можно рассматривать сокращение размерности внутри каждого кластера. Ковариационная матрица строится для векторов данного кластера. Переходя от кластера к кластеру, каждый раз устанавливают максимальное значение S , а затем с использованием (3) определяют квантование других осей и размерность пространства.

Рассмотрим пример. Анализируется изображение поверхности Земли со спутника NOAA 17 от 7.04.2003, полный кадр (1328x624) пикселей представлен в пяти спектральных каналах (один в видимой части спектра, остальные в инфракрасной), объем около 4 мегабайт. На рис. 4 можно видеть изображение в одном из каналов.

Визуальный анализ изображений в каждом спектральном канале показывает, что снизу-вверх слева-направо на рис. 4 видно формирование вихря (по форме напоминает дракона); в верхней части рис. 4 в основном – тающие снега, тайга Сибири. Кластеры с площадью меньше 100 пикселей отнесены в фоновый. Для большинства подкластеров размерность собственного пространства оказалась равна трем, как и для всех данных в целом, но некоторые подкластеры – 720 –

(соответствующие полупрозрачным облакам) потребовали пятиспектрального рассмотрения. Таким образом, сокращение размерности произошло более точно, в зависимости от характера области данных. Время вычислений оказалось в три раза меньше, чем для полного пяти-спекрального варианта, и составило несколько минут на одноядерном компьютере РК 1.6 ГГц 512 МБ.

Резюме

Иерархический гистограммный алгоритм с заданием отделимости каждого полученного кластера позволяет не только автоматически выбрать детальность представления данных, различную для каждого полученного кластера, но и сократить размерность пространства признаков в зависимости от области рассмотрения. Это приводит к существенному сокращению времени вычислений. Единственный параметр d определяет отделимость каждого полученного унимодального кластера. Чем меньше этот параметр, тем лучше отделены кластеры. Но с уменьшением d у величивается доля кластеров фона, т.е. не разделенных для данного d , и при некоторых d все кластеры сливаются в один фоновый. Доля этого кластера может служить индикатором остановки работы алгоритма.

Работа выполнена частично при финансовой поддержке Российского фонда фундаментальных исследований (проект № 16-07-00066) и Программы I.33П фундаментальных исследований Президиума РАН (проект № 0315-2015-0012).