GMM-based Imbalanced Fractional Whale Particle Filter for Multiple Object Tracking in Surveillance Videos

Visual tracking is a critical task in vision-based applications in which the actions of humans are identified, and the human-computer interfaces are developed. Stochastic point tracking methods employ a state-space approach to model the linear or non-linear dynamics of the objects using the Kalman filter or particle filter. The Kalman filter fails when vision tracking problems are non-linear, non-Gaussian, and multi-modal. The PF solves such vision problems, which rely on the recursive construction of the state space's posterior probability density function (pdf). A set of random particles is produced to estimate the posterior pdf of the states of the tracked objects. In estimating the states of objects, these sets of particles are updated and propagated based on sequentially arriving observations. The particle filter better estimates hidden state variables than the other non-linear filters [1, 2]. However, due to the resampling procedure, the particle filter suffers from the problem of sample degeneration and impoverishment propagating in state space [3]. The resampling technique involves replacing the old set of particles with related weights with the new set of particles with related weights in more probable regions of state space when sample degeneration increases above a threshold. The resulting sample impoverishment pertains to the frequent selection of particles with high weights and the dying out of other particles with negligible weights when particles propagate after each time step [4, 5].

The imbalanced surveillance video dataset consists of normal and anomalous instances. The normal and anomalous instances cause majority and minority samples associated with high and low probable regions. In the standard particle filter, the minority particles tend to be at high risk of being suppressed by the majority particles, as the biased proposal or importance pdf encourages only majority particles in the highly probable regions of the input data space. However, resampling tries to correct the bias to a small extent. The difficulty in designing the correct proposal or importance pdf prevents standard particle filter-based tracking in the imbalanced surveillance video data. Further, the problem of sample degeneration and sample impoverishment occurs due to the choice of a biased proposal or importance pdf ignoring the minority particles [6, 7].

Traditional tracking methods for imbalanced data suffer from the problem of occlusion and identity switching between objects. This problem worsens when the cost of tracking false negatives and false positives is the same. The resampling methods apply three actions for the imbalanced data: data, algorithmic, and hybrid-level. In this paper, multiple object tracking is based on hybrid-level actions on the majority and minority particles. This paper discusses converting the biased proposal or importance pdf into the unbiased proposal or importance pdf using hybrid-level action for the particle filter.

The authors [8] provided a theoretical justification for an evolutionary particle filter to prevent the problem of sample impoverishment without the application of visual tracking of the objects. The authors [9] proposed a whale optimization algorithm (WOA), which is a highly efficient swarm-based metaheuristic algorithm stimulated by the hunting behaviour of humpback whales (H-whales) and determine the best solution. The WOA avoids local optima and gets a global optimal solution. The WOA solves different constrained or unconstrained optimization problems for practical applications without reformulation in the algorithm. This algorithm is highly efficient compared to other metaheuristic algorithms and is found to help handle imbalanced data.

In keeping with the advantages of metaheuristic algorithms and fractional calculus in dealing with the problem of sample degeneration and impoverishment, this paper proposes a new fractional whale particle filter (FWPF) which fuses a novel fractional whale optimization algorithm (FWOA) [9] with the standard particle filter for multiple object tracking (MOT) in the imbalanced surveillance video data with tracking challenges. Multiple objects from the initial video frame are extracted through human intervention, and the particles and related weights are generated. Then, the particles are updated using the FWPF method. This operation is repeated until the best solution is determined. In this paper, contributions are as follows:

• •    Development of a complementary fractional whale particle filter (FWPF) that fuses the fractional calculus-based whale optimization algorithm and the standard particle filter under weighted sum rule fusion. Integrating the FWPF with an iterative Gaussian mixture model (GMM) with unbiased sample variance and sample mean allows the proposal or importance probability density function (pdf) to be adaptive to deal with the imbalanced nature of surveillance video data. The adaptive importance or proposal pdf leads the FWPF to a minimum variance unbiased estimator (MVUE) for effectively detecting and tracking multiple objects in the imbalanced surveillance video data. The novelty of the work is to convert the fixed biased proposal pdf into an unbiased adaptive proposal pdf to deal with imbalanced data.

• •    A novel imbalanced evaluation metric, tracking distance correlation (TDC), is employed to evaluate the bias and variance correction (imbalance reduction) caused by an unbiased proposal pdf in the imbalanced FWPF-based tracking over the biased proposal pdf in the standard particle filter-based tracking. Apart from TDC, other performance measures, such as multiple objects tracking precision and accuracy (MOTP and MOTA), the sample mean and variance are used for comparative evaluation with other existing methods in the presented work.

• 2.    Related Works

• 3.    Challenges

• 4.    Particle Filter Fundamentals

This paper is structured as follows: The second and third sections relate to the related works and the challenges, respectively. The fourth section recounts the mathematical formulations for the standard PF. The fifth section introduces the proposed FWPF for MOT in imbalanced surveillance video data. The sixth section details the results and discussion. Finally, the seventh section winds up the paper as the conclusion.

In particle filter-based visual tracking, the object's states are unknown and can only be deduced from visual feature observations. Visual tracking has two main difficulties: the state hypothesis evaluation of the observed image and the search for the state space. Metaheuristic algorithm-based particle filter tries to solve such problems in visual tracking. The two main visual tracking procedures are bottom-up and top-down procedures. The former typically favors rebuilding the states of the objects by examining the objects in the video sequences. At the same time, the latter is used to build and examine a state hypothesis set based on object models[10]. The MOT has many tracking challenges, such as occlusion, confusion between objects, scale changes of objects tracked, tracking resumption, and variability in the number of objects. There are two steps in MOT: In the first step, the number and position of targets are inferred from the current frame at every iteration, and this step requires either a generative or discriminative model, whereas the second step refers to the modelling of detection errors and the movement of the target [11]. The Markov-Chain-Monte-Carlo (MCMC) framework approximates the posterior pdf adaptively and estimates the best state of objects using the Markov chain. This method encounters the problems of sample degeneration and impoverishment while tracking multiple objects [12].

The authors [13] proposed an evolutionary particle filter using modified grey-wolf metaheuristics to resolve sample impoverishment. The method enhances exploitation and exploration properties in tracking. However, the technique had limited exploration of dynamic target object behaviors. In [14], authors proposed a chaotic local search model for irregular motion with fewer particles. A chaotic sampling procedure enhances particle distribution in high-likelihood areas. The method effectively handles occlusion and fast-motion challenges by introducing a histogram of dynamic information for motion representation. The method exhibits superior performance in comparison to leading-edge approaches in tracking accuracy. The method has limited exploration of chaotic optimization in higher dimensions. The authors [15] proposed the combination of quantum particle swarm and adaptive genetic metaheuristics to focus on interference factors affecting tracking efficiency and accuracy. The method effectively handles occlusion and fast motion. In [16], the authors proposed a Mean shift algorithm for particle prediction and modified particle swarm metaheuristics for detecting occlusions in dynamic environments. The anti-occlusion module in this method improves tracking performance during occlusions.

The authors [17] proposed the covariance matrix-based learning with biogeography-based metaheuristics for real-world object tracking utilizing suitability index variables and color histograms. In [18], the authors proposed mayfly position-weighting strategies and dynamic control for multi-target tracking. Additionally, chaotic optimization strategies enhanced velocity parameters in mayflies. This method required addressing new and faded targets. The authors [19] proposed an improved firefly algorithm for optimization for multitarget tracking addressing the particle filter's weight degradation issue. The method fell into premature convergence quickly. The authors [20] utilized convolutional features and superpixel segmentation to address challenges in target association during complex scenarios of intelligent transportation. The method lacks extensive evaluation of diverse datasets. In [21], the authors proposed an iterative particle filtering based on ant colony metaheuristics and locality-sensitive histogram models to address the target appearance under illumination variations. The method discussed an iterative unscented Kalman filter for proposal distribution. However, the technique does not explore real-time tracking applications.

The most difficult problem in visual tracking is the occlusion of objects, in which the portions of occluded objects are only seen, and the tracking becomes very difficult after the occurrence of object occlusion. The entry and exit of multiple objects in video sequences also pose problems for tracking systems. Tracking 3D visual persons has also been a challenging task in computer vision. Multiple object confusion leads to mismatches in tracking. Another difficulty is handling variable-size objects and their inter-occlusion in video sequences, affecting the tracking process in video surveillance and monitoring systems. The other challenges include noisy video data, changes in scene illumination, multicamera tracking, etc. The current literature does not address the imbalanced data issues of surveillance video data but suggests different techniques for multiple object tracking (MOT).

The main aim of the PF method is the estimation of a posterior pdf p ( x_n |y._n ) from a time-varying state-space model consisting of motion model specified by a state transition pdf p ( x_n |x_{n t}) and observation model specified by the observation likelihood pdf p ( y_n x ) ) where, x_n is the state vector of an object at discrete time-instant n , y _{l n} is the set of observations i.e. video frames from discrete time-instant 1 to the current discrete time-instant n , and y denotes the video frame at discrete time-instant n [1, 2, 3]. In the PF method, a posterior pdf or filtering pdf is computed according to prediction step and filtering or update step under the two-step recursion when a new video frame y is considered [4, 5]:

P ( x n | У 1: n - 1 ) = J P ( x n x - 1 ) P ( x n - 1 | У 1: п - 1 ) dx n - 1

P ( y_n\^x„ ) P ( ^xn| y _h-1 )

^P n ^У1'^П    J P ( У п xn ) P ( xn | У 1: п -1 ) ^dxn

But, the recursive computation of the above posterior pdf is not possible analytically. Instead, it is numerically

M approximated by a set of Я random particles with related weights w at discrete time-instant n , {xm, wm }  ^ and it is given as follows:

M

p ( Хп\У1п )°E wm3 ( xn - xm ) m=1

Where 3 ( • ) denotes the Kronecker delta function. The particles are random samples of the state vector, and the

M weights have non-negative values that sum up to unity, i.e. Z wm = 1 and are interpreted as probabilities of the particles.

m =1

In practice, we often cannot draw samples directly from a posterior pdf because it may not be a standard pdf. Instead, particles are easily drawn from an importance or proposal pdf n ( x_n |xm._n y_n) which is a biased pdf approximating the important regions of input variables. In (3), RHS is characterised as follows:

xm Dn (xn|xm-1, Уп)                                                        (4)

wm

w . = mt^~ Z w m m = 1

w

= Wn-1

p ( y.|x m ) p ( xm|x ~,)

n ( x m l

| xm-1, У.)

If the importance pdf is made equal to the state transition pdf, i.e. n(xm|xm—1,y. )=p(xmxmi) which, then, simplifies to the above equation as wm = w^p (yn x

:m). The initialization of PF requires the generation of a set of random particles, {xm, wm} ^ from the prior pdf p (x0). Equations (4) to (6) show the recursive computing of the set of random particles with related weights for the representation of p (xjy1:„) from the previous posterior pdf p (xn_1\y1.n_J corresponding to a new observation y . The number of efficacious particles is expressed as

M f =

M

Z( wm )2

m = 1

In the PF method, all the particles are assigned the exact weights, and at each discrete time-instant, the particles are propagated and assigned weights. As time evolves, degeneration of a set of particles occurs, and only a few particles are left with meaningful weights. A well-biased importance pdf and a resampling procedure can reduce the sample degeneration to a small extent. Still, it presents the supplementary challenges of sample impoverishment, resulting in a deficiency of sample diversity in the state space. Recursive update calculations of ineffective particles seriously degrade the performance of particle filters. The resampling procedure eliminates the small weighted random particles and replicates the large weighted random particles. This resampling procedure poses the problem of sample impoverishment due to the over-replication of large weighted random particles and the reduction in the number of meaningful particles. Finally, it becomes difficult for the new set of particles to keep track of the true states of targets. To overcome this problem, this paper proposes FWPF for MOT in surveillance video data.

• 5.    Proposed FWPF for Multi-object Tracking

• 5.1.    Object Extraction from the Input Video

• 5.2.    Multiple Object Tracking by Fractional Whale Particle Filter

Fig. 1 represents the proposed FWPF-based hybrid model for MOT in surveillance videos. The first step is object extraction, in which the objects are extracted from the video through manual intervention by considering the features of the objects. The next step is particle generation, in which the particles are generated randomly for the extracted object in each video frame. Then, particle updation is performed to select the position of the multiple objects in the video frame. The particle updation uses a hybrid model of standard particle filter and FWOA methods. The standard particle filter updates the particles by calculating the weight of each particle in the extracted object and discarding the particles with small weights. In this way, the particles are resampled, and the optimal position of the object is determined. WOA is a swarm-based metaheuristic that assumes the present solution is the best prey [9]. Then, the search agents update their position to the high likelihood region of the best search agent to find the optimal solution.

Let us assume that the proposed MOT method's input is a video consisting of n frames. The input video taken as input to the proposed method is represented as V = { V ;1 <  i <  n } where V represents the video and n represents the number of frames in the video. The primary task in the visual tracking is to discover the moving objects from the initial frame by extracting the foreground objects. The extracted object is then given for the tracking process, which involves the identification of the object's trajectories. So, the MOT method requires an object extraction mechanism either from the initial frame of the video or when the object appears initially in the video. In this MOT method, the object is extracted manually from the video sequence at the initial frame. The detected objects from the video through manual intervention are denoted as O = { O_} ;1 <  j <  k } where O represents the multiple objects set and k represents the number of objects presented in the input video V .

The preprocessing technique is based on weakly supervised object detection (WSOD). An adaptive background subtraction approach is employed to initialize the detection of moving objects over the frames. After moving objects are detected in the initial frames with little human intervention, they are weakly labelled as objects or non-objects by applying a distance-based classification method, and the same is continued in successive frames within the small spatiotemporal neighbourhood. With known positions and weak labelling for objects or non-objects, real-world video datasets are always unlabelled and imbalanced because they contain anomalies somewhere in the frames, and their exact locations are unknown. These weakly labelled objects are refined and localized by the weighted sum rule fusion of the complementary trackers for multiple objects over the frames. The WSOD-based complementary trackers (FWPF and standard PF) are suitable for unlabelled and imbalanced video datasets where limited data availability is a major concern.

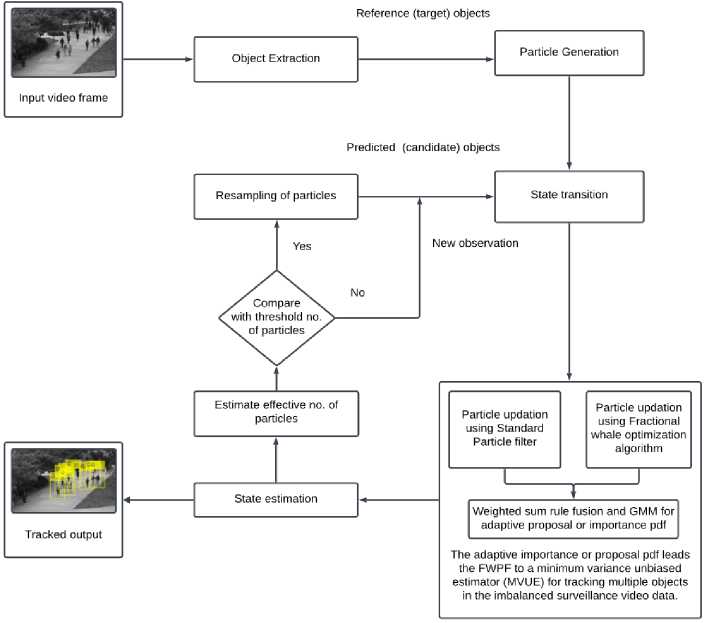
Fig.1. A proposed fractional whale particle filter method for MOT in the surveillance video

This section describes the particle updating process in which the particles are updated using the standard particle filter and fractional calculus-based WOA method. Given the problem of sample degeneration and impoverishment in standard particle filters, the weighted sum rule fusion of FWOA and standard particle filter allows the biased proposal or importance pdf to be adaptive using the iterative Gaussian mixture model (GMM) with unbiased sample variance and sample mean.

• A.    Generation of Initial Particles

The particles are generated for every object after detecting the position of every object in the initial frame. Here, every object O contains v number of particles. The particles corresponding to every object are generated randomly to evaluate the system's initial states. Here, the particles are used to describe the spatial and temporal attributes of moving objects in the video frames, and the particles are sampled based on the importance of the pdf.

• B.    Updating of Particles by Particle Filter for Visual Tracking

Once the particles are located in the initial frame, the movement (updating) of the particle is to be found to obtain the objects' location in the next frame. In a standard particle filter, the weight of each particle is determined based on the spatial and pixel correspondences. The spatial correspondence is computed based on the location of the objects using the Euclidean distance, and the pixel correspondence is computed based on the object's intensity using the Bhattacharyya distance. Once the weights of every particle are computed, they are multiplied by the previous position of the particle to find the location in the next frame. The new position of the object O at time T is determined as,

v

p^( F) = Z MTCT u =1

Where v is the number of particles, is the centre of the particle u at time T and M ^T is the weight of the particle u at time T . Here, the determination of the weight of each particle depends on the spatial pdf, p ( B T | C T ^T ) and the colour pdf, p ( D T | C T ) . The weight of the particle u at time T is determined as follows:

p (BjCu) p (DjCu)

v

Z p (BjCe) p (DjCe)

e = 1

The spatial pdf, p ( B T | C T ) is determined as follows:

p ( B O C T )

1 - k ( y ( C T ) , y ( P OT ^{- 1} ) )

H

Where, y ( C T ) is the centre of C T and y ( P T ¹ ) is the centre of P T ¹ . k ( • ) represents the Euclidean distance between y ( C T ) and y ( P T ^{- 1} ) . The denominator H in the above equation is computed based on the mean distance of the object region S located in the previous video frame with the height q and width p .

H =

7Sp (PT;')’+ Sq (PT')2

Then, the color pdf, p ( D T C T )

is calculated as follows,

p (DOjCT)  =  1 — W (g (PO^), g (CT))

Where, W ( • ) represents the Bhattacharyya distance obtained from (13). g ( P T ¹ ) and g ( C T ) denote the number of pixels in the bounding box surrounding the position of the object O_j at time ( T - 1), i._e. P T ^{- 1} _and C T , respectively.

Once the weights are computed, the particles which have lower weights are eliminated to improve the tracking accuracy. The remaining particles are the new set of particles for the next iteration. When a new set of particles is sampled, failure in the tracking gets repaired in the next few frames. In this way, the particles are resampled, and the object's new position is determined iteratively. The estimated result is applied to minimize the search area and the computation time during tracking.

• C.    Updating of Particles by Fractional-whale Optimization

The original whale optimization algorithm (WOA) copies the social behavior of the H-whales, which identifies the prey’s location and encircles them. Since the placement of the optimal solution is unfamiliar at the beginning, the WOA assumes the present solution as the target solution, beginning with a set of random solutions. Each iteration updates the search agent’s position by either a randomly selected agent or the optimal solution. The process is repeated till it reaches the best solution. However, the WOA has a limited global search and a slow convergence rate [9].

The imbalanced surveillance video dataset introduces the drawbacks of overlapping objects during multiple object tracking, which causes problems with between-object imbalance and within-object imbalance with some missing or incomplete data. Such object imbalances occur when minority particles associated with low probable regions are not well separated from majority particles associated with high probable regions in specific areas of the input data space due to incomplete data. To counter this problem, the position of the particles is updated by the Fractional-whale optimization algorithm (FWOA), which aims to search the nearby position of the particles in the next frame to find the optimal position of the objects. This algorithm integrates the fractional calculus up to the first four terms, also known as adaptive multiple variable polynomials (AMFP), with the position update process of the whale optimization algorithm [22, 23].

The FWOA is a local and global search operator with inherent memory property. The FWOA adjusts the distribution of between-object and within-object generated particles using multiple imputation-based oversampling of minority particles in the targeted specific area of the input data space. The AMFP generates multiple different imputations for each missing data. If the missing or incomplete data are multivariate, they can be imputed from a joint multivariate normal or log-linear model. The AMFP imputes each majority particle only once for its missing data, whereas it oversamples each minority particle by replacing it with multiple imputations. Thus, all incomplete data are imputed with the oversampling of minority particles. One significant advantage of AMFP is that the oversampled minority particles are diversified with multiple imputations to eliminate data distortion, and all the observed data are kept unmodified. The FWOA approach results in low-bias and low-variance with greater efficacy for tracking precision and tracking distance in the imbalanced surveillance video dataset [24, 25].

• i.    Solution Encoding: Every solution is represented by a two-dimensional vector that indicates the position of the particles in the next frame.

• ii.    Fitness Calculation: The fitness is used to evaluate whether the generated solution is better. The fitness of every solution is calculated using the Bhattacharyya distance, which is given as follows:

  Fitness =

  
  

  -Yj/jmj—

  Г jUjj)

  
  
  
  

Where l and m represent the position of search agents in the present video frame and previous video frame, respectively.

• iii.    Algorithm: The algorithm for FWOA is explained below:

• a.    Initialization: The search agents are initially populated randomly and initiate their position randomly by surrounding the object’s position. This process kicks up the search agents to move toward the likelihood region of the objects placed in the previous frame.

• b.    Fractional encircling prey: H-whales identify the prey’s location and encircle them to find the position in the next iteration. In the shrinking encircling phase, the new position of the search agents is computed as follows:

G ( r + 1 ) = (1 - H . F)G ( r ) - H-( a G ( r ) + - a G ( r - 1) + - a ( 1 - a ) G (r - 2) + — a ( 1 - a )( 2 - a ) G ( r - 3)

I          2            6                   24

Where G ^* and G are the position vectors corresponding to the best solution and the search agent with r as the current iteration. H and F are both coefficient vectors. The encircling prey is modified with fractional calculus up to the four terms with fractional order of a to be in the range of 0 <  a <  1. The fractional calculus is based on the generalized Grunwald-Letnikov Equation for the discrete fractional derivative with fractional order of a [24, 25].

Then, the updation of the coefficient vectors H and F are computed as follows:

H = 2 hi - s - h

F = 2 - s

Where, h linearly decreases in the range [ 2 ^ 0 ] over the iterations, and 5 is a random vector in the range [ 0,1 ] . c. Fractional exploitation phase: In the spiral updating position phase, the new position of the search agents is computed based on the following equation:

G ( r + 1 ) = ( 1 + e d • cos ( 2 n f ) ) G *( r ) - e d • cos ( 2 n f ) •

aG(r) + — aG(r -1) + — a (1 - a) G(r - 2) +

a (1 - a)( 2 - a) G(r -3)

Where d is a constant denoting the state of the logarithmic helix in the range, f is a random number [-1,1] and ' • ' is the element-wise multiplication. In the shrinking circling mechanism, the position of H-whales is updated as per (13) and (17) when the random probability of occurrence is less than or greater than p = 0.5 .

• d.    Fractional exploration phase: The search agents search for prey (perfect solution) randomly, and the position of the search agent is updated based on the position of other search agents. This can be represented as:

G(r + 1) = (1 - H F)Gm - H • (aG(r) + 1aG(r - 1) + 1a(1 - a)G(r - 2) + ^aQ - a)(2 - a)G(r - 3)) (18)

Where, G m is specified as a random position vector.

• e.    Termination: The FWOA is performed between either a circular or spiral movement, considering the value of p . Then, the process is repeated until it reaches the maximum number of iterations the user gives. After reaching the maximum iteration, the best prey location is assigned to P T ( FW ) , which is the position of the particle in the next frame.

• D.    Weighted Sum Rule Fusion for Updating the New Position

The new position obtained through the PF and FWOA is combined with the weighted sum rule fusion to track multiple objects in the video sequence. The fusion provides the mean position of the PF and FWOA as the final tracking paths of the multi-objects. The following equation determines the new position of the object:

P T ( PF ) + P ( FW )

P T = X n

N = 2

N =2

Z = ^ a Xi such that ^ a. = 1, and

i =1                                       i =1

N =2

2    2 2   22.22

a ₇ = >  a. a _Y = a &  y + a .a _y

Z             i   Xi       1X12X2

i =1

Where P T ( PF ) is the new position of the object obtained by the PF method and P T ( FW ) is the new position of the object obtained by the FWOA. Since P T ( PF ) and P T ( FW ) are originated from the same video frame (data) distribution; they are not independent but are uncorrelated due to the FWOA-based tracker being complementary to the PF-based tracker. When treated as uncorrelated random variables, these complementary trackers produce a minimum variance, undergoing weighted sum rule fusion with equal weighting coefficients. If these complementary trackers achieve minimum variance for multiple objects, it will result in higher precision. The other score-level fusion techniques, like the maximum rule, minimum rule, product rule, median rule, etc., are not applied because these trackers are not independent [26, 27].

The weighted sum rule fusion is based on optimization by complementarity. One tracking model's incorrect detection and localization are complemented by another. If the trackers complement each other, they cancel out each other's random errors and help output correct or unbiased detection. These complementary trackers are uncorrelated but not independent because they originate from the same video frame (data) distributions. These trackers cause two complementary events which are mutually exclusive to each other. These trackers undergo the weighted sum rule fusion as per (19), where the terms Xt and a. are uncorrelated random variables (two complementary trackers) and real weighting constants. The term Z is another random variable formed through weighted sum rule fusion. Further, we obtain the expression of the variance of Z in terms of the variances of X and X as given in (19). In statistics, precision is the reciprocal of the variance. In order to verify the approximated values of the precision, we assume a2 = a22 = a2 and consider different values of a and a . With a = a = 0.5 , it is found that the averaging of two complementary trackers I Z = —1-^—2 I results in higher precision I MOTP « E- I.

I         ° Z J

• E.    Adaptive Proposal pdf for the Imbalanced Data

The imbalanced surveillance video dataset consists of majority and minority classes as normal and anomalous instances. The normal and anomalous instances cause majority and minority samples associated with high and low probable regions. The minority particles tend to be at high risk of being suppressed by the majority particles, as the proposal or importance pdf encourages the highly probable regions of the input data space to remain a “biased distribution” in the standard particle filter. The proposal or importance sampling depends entirely on the choice of biased distribution, which results in a biased estimation of the discrete random measure. However, true and normalized importance weights are introduced to correct the bias to a small extent. The difficulty in designing the correct proposal or importance pdf prevents the use of particle filtering-based tracking in the imbalanced surveillance video dataset. Further, the standard particle filter tracker suffers from the problem of sample degeneration and sample impoverishment due to the biased proposal or importance pdf ignoring the minority particles [28, 29].

To alleviate this problem, The FWOA is fused with the standard particle filter under the weighted sum rule fusion to represent the proposal or importance pdf as a mixture of Gaussian distributions to deal with highly non-Gaussian true posterior pdf in the imbalanced data. Thus, FWOA adapts each component's weights and parameters in the GMM to result in the adaptive proposal or importance pdf for the FWPF, which balances exploring new areas of the state space with exploiting promising regions [30, 31].

M i. Further to (19), a set of M random particles with associated weights u at discrete time-instant n , {xm, um}   is considered to denote x 1 and xM as best (with a small selection pressure coefficient, a ) and worst (with a large selection pressure coefficient, a ) initial solution, whereas the associated weight u^ is defined to be Gaussian distributed with constraint as under:

2 2aaM

M

> such that E u ^ = 1

m = 1

• ii.    The GMM, as the importance or proposal pdf, is generated for every p^th observations with Gaussian probability density function, characterized by the mean ( p )and variance ( ст ²) as follows:

M2

G n { x m ( p ) } = e< n ( x m ( p ); p m ( p ), ( a m ( p ) ) ) m = 1

N ( x ; p , a ²) = —exp <

⁽     ) 2 CT

1 ( x - p

21 ст

Where x ( p )denotes the p^th element of the vector x . The unbiased sample mean and sample variance for the observations drawn from the Gaussian pdf are defined as follows:

M pm ( p )=xm ( p )=- E xm ( p )

M m = 1

M2

^{CT m ( p ^)} = M — 1₎ E ^{ x m ( p ^{) -} x m ( p ^)}

• iii.    Thus, the GMM generates N new samples that represent the progeny of the primary population. The most optimal function is assessed for all the newly generated samples. The M ^eff fittest solution among the M current samples and N new samples are formed to find the best solution. The adaptive importance or proposal pdf, G_n ( x m ) now modifies (6) with (21) and (22) as follows:

Q

G n ( x m ) = П G n ( x m ( p ) ) = G ( x m ( 1 ) ) ^{x G} 2 ( x m ( ² ) ) ^x-^x g Q ( x m ( Q ) )                  (25)

p = 1

M

M Z p(yn\xm) p(xm\x„-1)

Once the weights are modified according to adaptive importance or proposal pdf, the particles { ^xm , w m } M = 1 ^are completely updated/resampled based on the modified posterior pdf from (3) till the completion of the epoch n as follows:

M p (x-kn )DZ wm^ (xn - xm) m=1

• 6.    Results and Discussion

  The proposed approach is simulated using the "MATLAB2019b" software tool on a system with an "Intel" core processor and 2 GB RAM, as well as the "Windows-11" operating system. The imbalanced UCSD video data – 1 and 2 [32] are obtained using a stationary camera mounted on the building, observing the pedestrian walkways where the density varies from sparse to crowded. Some occlusions and scale changes cause anomalies like cyclists, carts, and skateboarders to move at nonlinear speed. Each video has 100 frames with an image resolution of $158 \times 238$ pixels. The reason behind considering this video data is that the camera's field of view leads to a heightened degree of perspective distortion and pronounced variations in the scale of moving objects. Furthermore, anomalous events encompass motion anomalies elicited by cyclists, carts, and skateboarders, as well as contextual anomalies. The simulation results are discussed in this section.

• 6.1.    Evaluation Metrics

Multiple objects tracking accuracy (MOTA) can reveal how class imbalance affects the overall tracking performance. For instance, a disproportionately high false negative rate for a minority class could indicate that the tracker consistently struggles to detect or maintain tracks of these minority or anomalous objects. In statistics, precision is often defined as the inverse of variance. Intuitively, variance measures how spread out a set of values is from its mean, while precision indicates how close or concentrated those values are to the mean. As a minimum variance unbiased estimator, the proposed method considers the Multiple objects tracking precision (MOTP), which can assess how accurately the tracker localizes those objects, regardless of their frequency in the video. Tracking distance correlation (TDC) can assess object tracks' temporal consistency and reliability. This is particularly important when dealing with imbalanced video data, where the performance of minority or anomalous objects might be compromised.

• A.    Multiple Object Tracking Accuracy (MOTA)

This metric incorporates three types of errors: false negatives, false positives, and identity mismatches. For the most accurate tracking, a high MOTA value is desired. The total count of ground truth objects is GT at frame (time) t . The terms FN , FP , and IDMM are the number of false negatives, false positives, and identity mismatches at frame (time) t , respectively [33, 34].

^ ( FN_t + Fp + IDMM_t )

MOTA = 1 — t--------

Z GTtt

• B.    Multiple Object Tracking Precision (MOTP)

The metric refers to the average difference between all true positives and their ground truth hypothesis. A high MOTP value is preferred for the most precise tracking. The average dissimilarity among all true positives and their corresponding ground-truth hypothesis is the Multiple Object Tracking Precision [33, 34].

Z d , i

MOTP = -t^— Z c, t

Where the terms d and c are the bounding box overlap of the target i with its assigned ground truth object and the count of matches at frame (time) t , respectively. It is used to represent the ability of the tracker to evaluate the correct position of the object positions in a video frame. MOTP and MOTA values vary between 0 (no tracking) and 1 (fully tracked). Higher values of both MOTP and MOTA are desirable for accurate and precise tracking.

• C.    Tracking Distance Correlation (TDC)

• 6.2.    Experimental Results

This metric measures both linear and nonlinear association between the original tracking path ( X ) and algorithmic tracked path ( Y ) in the imbalanced particle filter-based tracking. TDC value varies between 0 (when two paths are the same) and 1 (when two paths are independent). This metric depends on distance covariance, and its minimum value shows the bias and variance correction from tracking based on a biased proposal pdf to tracking based on an unbiased proposal pdf as required for FWPF. The tracking distance correlation is represented as follows [35]:

TDC ( X , Y ) = 1 — ^TDCov ( X , ^Y )

TDVar ( X ) TDVar ( Y )

Where TDCov ( ■ ) and TDVar ( • ) represent the paths’s distance covariance and distance variance.

The performance of the proposed method is evaluated using two videos obtained from the UCSD dataset [32], each containing 100 frames. The UCSD video datasets are considered limited, unlabelled, real-world imbalanced surveillance video datasets. Figs. 2 (a) and (c) represent the 7th, 21st, and 35th frames of video-1 (Bicycle) and video-2 (Cart). The experimentation is performed to track the different numbers of multiple objects (from one to eight) from video-1 and video-2, as shown in Figs. 2 (b) and (d).

Fig.2. Proposed FWPF-based tracking over the original frames 7, 21, and 35 of the (a, b) UCSD video data – 1 [32] and (c, d) UCSD video data – 2 [32]

• 6.3.    Performance Analysis

This section presents the comparative performance evaluation of the proposed FWPF with the existing methods like standard PF [1], Modified grey wolf particle filter (MGWPF) [13], Adaptive chaotic sampling particle filter (ACPF) [14], and Quantum particle swarm genetic particle filter (QPGPF) [15] when applying on the 100 frames extracted from UCSD video data – 1 and 2 [32].

• A.    Evaluation based on MOTP

Table 1 compares the average MOTP values of the proposed FWPF method with the existing methods [1, 13, 14, 15]

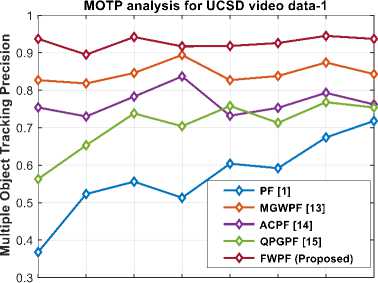
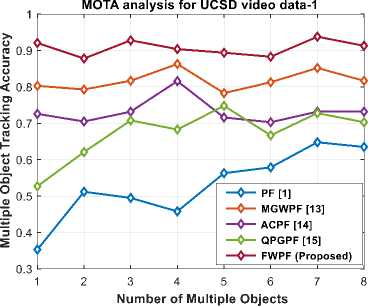
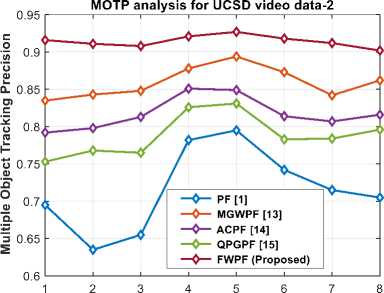
for the different numbers of individual tracked objects (from one to eight) in UCSD video data-1 and 2. Figs. 3 (a) and (c) depict the MOTP analysis curve for UCSD video data -1 and 2, respectively. The proposed method attains an average MOTP of 92.71% for UCSD video data -1, outperforming the MOTP values of 56.85%, 84.58%, 76.80%, and 70.63% achieved by PF, MGWPF, ACPF, and QPGPF, respectively. Similarly, the proposed method attains an average MOTP of 91.43% for UCSD video data -2, outperforming the MOTP values of 71.55%, 85.93%, 81.75%, and 78.82% achieved by PF, MGWPF, ACPF, and QPGPF, respectively.

• B.    Evaluation based on MOTA

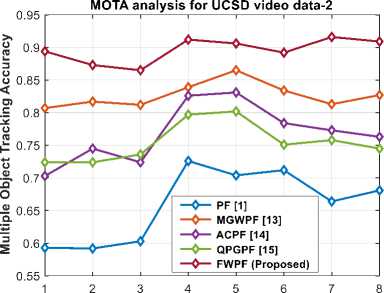
Table 1 compares the average MOTA values of the proposed FWPF method with the existing methods [1, 13, 14, 15] for the different numbers of individual tracked objects (from one to eight) in UCSD video data-1 and 2. Figs. 3 (b) and (d) depict the MOTA analysis curve for UCSD video data -1 and 2, respectively. The proposed method attains an average MOTA of 90.73\% for UCSD video data -1, outperforming the MOTA values of 53.03%, 81.76%, 73.27%, and 67.31% achieved by PF, MGWPF, ACPF, and QPGPF, respectively. Similarly, the proposed method attains an average MOTA of 89.58% for UCSD video data -2, outperforming the MOTA values of 65.93%, 82.67%, 76.86%, and 75.46% achieved by PF, MGWPF, ACPF, and QPGPF, respectively.

1       2       3       4       5       6       7       8

Number of Multiple Objects

(b)

(a)

Number of Multiple Objects

(c)

Fig.3. (a, b) MOTP and MOTA analysis curve and (c, d) MOTP and MOTA analysis curve for the UCSD video data - 1 and 2 [32]

Number of Multiple Objects

(d)

• C.    Evaluation based on TDC

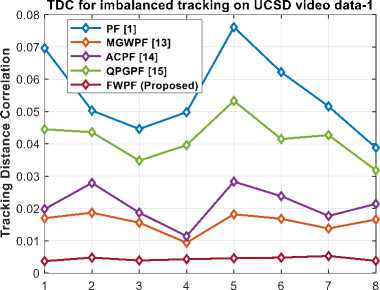
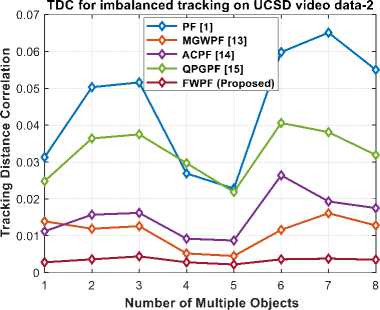
  Table 2 compares the tracking distance correlation (TDC) values of the proposed FWPF method with the existing methods [1, 13, 14, 15] for the different numbers of individual tracked objects (from one to eight) in UCSD video data-1 and 2. Figs. 4 (a) and (b) depict the TDC analysis curve for imbalanced tracking over UCSD video data -1 and 2, respectively. The proposed method attains TDC value of 0.0038 (for tracking of eight multiple objects) for UCSD video data -1, outperforming the TDC values of 0.0388, 0.0166, 0.0214, and 0.0318 achieved by PF, MGWPF, ACPF, and QPGPF, respectively. Similarly, the proposed method attains TDC value of 0.0035 (for tracking of eight multiple objects) for UCSD video data -2, outperforming the TDC values of 0.0550, 0.0128, 0.0175, and 0.0319 achieved by PF, MGWPF, ACPF, and QPGPF, respectively.

Table 1. MOTP and MOTA comparison of methods in UCSD video data-1 and 2

Video	Methods	Average MOTP	Average MOTA
UCSD video data - 1 [32]	PF [1]	56.85	53.03
	MGWPF [13]	84.58	81.76
	ACPF [14]	76.8	73.27
	QPGPF [15]	70.63	67.31
	FWPF (Proposed)	92.71	90.73
UCSD Video data - 2 [32]	PF [1]	71.55	65.93
	MGWPF [13]	85.93	82.67
	ACPF [14]	81.75	76.86
	QPGPF [15]	78.82	75.46
	FWPF (Proposed)	91.43	89.58

Table 2. Tracking distance correlation for imbalanced tracking of (1 to 8) multiple objects over UCSD video data – 1 and 2

Video data	Methods	Tracking distance correlation for imbalanced tracking of (1 to 8) multiple objects over video data
		1	2	3	4	5	6	7	8
UCSD-1 [32]	PF [1]	0.0696	0.0503	0.0446	0.0498	0.0761	0.0622	0.0516	0.0388
	MGWPF [13]	0.0170	0.0187	0.0156	0.0094	0.0182	0.0168	0.0138	0.0166
	ACPF [14]	0.0198	0.0279	0.0187	0.0114	0.0283	0.0238	0.0177	0.0214
	QPGPF [15]	0.0445	0.0436	0.0348	0.0396	0.0533	0.0415	0.0427	0.0318
	FWPF (Proposed)	0.0037	0.0048	0.0039	0.0043	0.0046	0.0048	0.0053	0.0038
UCSD-2 [32]	PF [1]	0.0313	0.0503	0.0516	0.0269	0.0228	0.0598	0.0651	0.0550
	MGWPF [13]	0.0139	0.0119	0.0126	0.0052	0.0045	0.0116	0.0161	0.0128
	ACPF [14]	0.0112	0.0157	0.0162	0.0092	0.0087	0.0264	0.0193	0.0175
	QPGPF [15]	0.0248	0.0364	0.0375	0.0297	0.02185	0.0406	0.0381	0.0319
	FWPF (Proposed)	0.0028	0.0036	0.0044	0.0028	0.0022	0.0036	0.0038	0.0035

Number of Multiple Objects

(a)

Fig.4. (a, b) Tracking distance correlation for imbalanced tracking on the UCSD video data – 1 and 2 [32]

(b)

• D.    Evaluation based on Sample Mean and Sample Variance

  Tables 3 and 4 compare the sample mean and sample variance of the proposed FWPF method with the existing methods [1, 13, 14, 15] when applied over the imbalanced UCSD video data-1 and 2. The proposed method attains minimum sample mean and variance of 0.0044 (close to zero) and 3.25714 x 10^-7 for UCSD video data - 1, as compared to sample mean (sample variance) values of 0.0554 (1.62203 x 10^-4), 0.0157 (8.8856 x 10^-6), 0.0211 (3.1324 x 10^-5), and 0.0415 (4.25221 x 10^-5) achieved by PF, MGWPF, ACPF, and QPGPF, respectively. Similarly, the proposed method attains minimum sample mean and variance of 0.0033 (close to zero) and 4.82679 x 10^-7 for UCSD video data - 2, as compared to sample mean (sample variance) values of 0.0454 (2.57158 x 10^-4), 0.0110 (1.68079 x 10^-5), 0.0155 (3.45568 x 10^-5), and 0.0326 (4.56215 x 10^-5) achieved by PF, MGWPF, ACPF, and QPGPF, respectively.

Table 3. Sample mean and sample variance for imbalanced tracking of multiple objects (multiple observations) over UCSD video data -1

Methods	Sample mean	Sample variance
PF [1]	0.0554	1.62203 x 10-4
MGWPF [13]	0.0157	8.88560 x 10-6
ACPF [14]	0.0211	3.13240 x 10-5
QPGPF [15]	0.0415	4.25221 x 10-5
FWPF (Proposed)	0.0044	3.25714 x 10-7

Table 4. Sample mean and sample variance for imbalanced tracking of multiple objects (multiple observations) over UCSD video data -2

Methods	Sample mean	Sample variance
PF [1]	0.0454	2.57158 x 10-4
MGWPF [13]	0.0110	1.68079 x 10-5
ACPF [14]	0.0155	3.45568 x 10-5
QPGPF [15]	0.0326	4.56215 x 10-5
FWPF (Proposed)	0.0033	4.82679 x 10-7

• E.    Evaluation based on Bias-variance Correction for Imbalance Reduction

Tables 5 and 6 compare the bias-variance correction for imbalance reduction by the proposed FWPF method to the existing methods [1, 13, 14, 15] when applied over the imbalanced UCSD video data-1 and 2. The proposed method attains the correction of bias (variance) by -92.06% (-99.79%), -72.12% (-96.33%), -79.21 (-98.96%), and -89.40 (99.23%) for imbalance reduction over UCSD video data - 1 when compared to PF, MGWPF, ACPF, and QPGPF, respectively. Similarly, the proposed method attains the correction of bias (variance) by -92.64% (-99.81%), -69.90% (97.12%), -78.53 (-98.60%), and -89.77 (-98.94%) for imbalance reduction over UCSD video data - 2 when compared to PF, MGWPF, ACPF, and QPGPF, respectively.

Table 5. Bias-variance correction (imbalance reduction shown with negative sign) by the proposed method (FWPF as minimum variance unbiased estimator) in comparison with other methods for imbalanced tracking over UCSD video data -1

Methods	Bias correction (%)	Variance correction (%)
PF [1]	-92.06	-99.79
MGWPF [13]	-72.12	-96.33
ACPF [14]	-79.21	-98.96
QPGPF [15]	-89.40	-99.23

Table 6. Bias-variance correction (imbalance reduction shown with negative sign) by the proposed method (FWPF as minimum variance unbiased estimator) in comparison with other methods for imbalanced tracking over UCSD video data -2

Methods	Bias correction (%)	Variance correction (%)
PF [1]	-92.64	-99.81
MGWPF [13]	-69.90	-97.12
ACPF [14]	-78.53	-98.60
QPGPF [15]	-89.77	-98.94

• F.    Evaluation based on Computational Time and Limitations of Methods

• 6.4.    Discussion

• 7.    Conclusions

Table 7 compare the computational time of the proposed FWPF method as compared to the existing methods [1, 13, 14, 15] when applied over the imbalanced UCSD video data-1 and 2. The proposed method processes the 100 frames each of UCSD video data-1 and 2 in 55.993 seconds and 25.775 seconds, respectively. The computational time is the lowest compared to the existing methods. The proposed method is suitable for limited (short-duration) video data obtained from fixed surveillance cameras under weakly supervised object detection settings. The limitations of other competing methods are as follows. In PF-based method, grid-based methods require a predefined state space, limiting uneven partitioning for high-probability density regions without prior knowledge. It highlights that the variance of importance weights increases over time, making degeneracy unavoidable. The computational cost of grid-based methods increases dramatically with state space dimensionality [1]. The MGWPF-based method may face challenges in motion blur and fast motion scenarios, leading to sample degeneracy. The convergence of the MGWO-PF algorithm can vary across different datasets, affecting performance consistency [13]. In the ACPF-based method, local representations fail to capture complex appearances effectively. Global representations are not robust to partial occlusions. Errors tend to accumulate during object model updates, leading to tracking failures under occlusions. The complexity and cost of global search pose an issue [14]. In the QPGPF-based method, the complexity of feature selection strategies is mentioned as a burden on computational efficiency. The position updating equation has some limitations in optimizing the particle distributions with imbalanced video data. This method incurs higher computational costs despite improving target positioning accuracy [15].

Table 7. Computational time (in seconds per 100 frames of UCSD video data-1 and 2)

Methods	UCSD-1 [32]	UCSD-2 [32]
PF [1]	493.756	176.107
MGWPF [13]	119.621	54.758
ACPF [14]	145.072	67.198
QPGPF [15]	404.676	168.769
FWPF (Proposed)	55.993	25.775

The proposed method is not meant for real-time tracking. Instead, it is used for limited, unlabelled real-world imbalanced video datasets. The limited video data from CCTV cameras for a particular time duration can be of important investigation by the law-enforcement authorities. Further, weakly labelled training data is generated using weakly supervised object detection. The weighted sum rule fusion of complementary trackers can further refine the localization of multiple objects. The proposed method tries to convert imbalanced tracking with a biased proposal pdf into balanced tracking with an unbiased proposal pdf in limited, unlabelled, real-world imbalanced video datasets. The conditions of extreme data imbalance with noisy input are generally found in the limited video data footage obtained from the video surveillance camera for a particular time duration. Weakly supervised object detection and refined localization by fusion of complementary trackers result in a better tracking model that deals with the imbalance in the limited video data footage [36]. As a minimum variance unbiased estimator, the proposed method exhibits bias-variance correction as an imbalance reduction factor, as shown in Tables 5 and 6.

The higher values of MOTP and MOTA are attained by the proposed FWPF method because it fuses the fractional calculus-based whale optimization algorithm and the standard particle filter under weighted sum rule fusion. Integrating the FWPF with an iterative Gaussian mixture model (GMM) with unbiased sample variance and sample mean allows the proposal or importance pdf to adapt to the imbalanced nature of surveillance video data. Thus, there are two trackers, one based on particle filter with a biased proposal or importance pdf and another based on FWOA with the adaptive proposal or importance pdf. Since these two trackers operate on the same video frame (data) distribution, they are not independent but are uncorrelated due to their complementary nature. These trackers deal with two complementary video data distributions that are mutually exclusive. These two trackers' weighted sum rule fusion leads the FWPF to a minimum variance unbiased estimation for effectively detecting and tracking multiple objects in the imbalanced surveillance video data. Since multiple objects are extracted with human intervention in the initial frame, making them weakly labelled (object or non-objects), the weighted sum rule fusion improves both MOTP and MOTA (with lowest TDC) over the frames due to the minimum variance achieved by these trackers being complementary. The FWPF, being an unbiased estimator, also results in the higher MOTP and MOTA overcoming the challenges of the imbalanced surveillance videos. The proposed method solves the problems of sample degeneration and impoverishment along with other tracking problems, such as scale change of objects tracked, occlusion, tracking resumption, etc [30, 31]. To justify the claim of the proposed method acting as a minimum variance unbiased estimator, the sample mean obtained from the multiple observations with different numbers of objects (from one to eight) is determined to be close to zero (unbiased) with minimum variance. The proposed method justifies the imbalance reduction through the bias-variance correction based on sample mean and sample variance obtained for multiple observations. The bias-variance correction (imbalance reduction) is attributed to an unbiased proposal pdf in the imbalanced FWPF-based tracking.

This paper fuses the fractional calculus-based whale optimization algorithm (FWOA) and the standard particle filter under weighted sum rule fusion. The fractional calculus up to the first four terms, known as adaptive multiple variable polynomials, makes the FWOA a local and global search operator with inherent memory property. Integrating the FWPF with an iterative Gaussian mixture model (GMM) with unbiased sample variance and mean allows the proposal or importance pdf to be adaptive to deal with the imbalanced surveillance video data, which is highly nonlinear and nonGaussian. Thus, there are two trackers, one based on particle filter with a biased proposal or importance pdf and another based on FWOA with the adaptive proposal or importance pdf. In view of operating on the same video frame (data) distribution, these trackers are not independent but are uncorrelated due to their complementary nature. These two complementary trackers' weighted sum rule fusion leads the FWPF to a minimum variance unbiased estimation for effectively detecting and tracking multiple objects in the imbalanced surveillance video data. Since multiple objects are extracted with human intervention in the initial frame are weakly labelled (object or non-objects), the weighted sum rule fusion of these complementary trackers causes minimum variance, improving both MOTP and MOTA over the frames. The proposed method handles sample degeneration, impoverishment, and other tracking challenges, such as scale change of objects tracked, occlusion, tracking resumption, etc. The resultant tracker, FWPF, achieves a higher MOTP of 92.71% (91.43%), MOTA of 90.73% (89.58%), TDC of 0.0038 (0.0035) for tracking of eight multiple objects in the imbalanced UCSD surveillance video data-1 (2) and outperforms the existing methods. The consistent tracking distance correlation near zero values infers the bias-variance correction for efficient imbalance reduction by the proposed method.

Acknowledgement

I confirm that the presented research work is the author's individual work. I also attest to the validity and legitimacy of the data and its interpretation. There are no conflicts of interest present, either with any individual or the organization.