Годограф локального фазового центра излучающего элемента навигационной антенны Глонасс

Спутниковая радионавигация системы ГЛОНАСС при определении местоположения объекта основывается на измерении расстояний, так называемых псевдодальностей, между космическим аппаратом и абонентом-приемником. При этих измерениях используют несколько способов определения дальности: по измерениям кода фазы (фазовая задержка кода) и/или по измерениям фазы несущей сигнала [1].

Радиосигнал, приходящий от спутника к абоненту, при изменении направлений по углу места и азимуту имеет различную задержку передаваемого кода и фазы несущей. Эти отличия обусловлены тем, что положение локальных (или частичных) фазовых центров (ЛФЦ) изменяются при изменении направления прихода сигнала [2].

Помимо определения точного положения ЛФЦ для каждого направления приходящего сигнала, не менее важным для измерения кодовых псевдодальностей является информация об изменении группового времени запаздывания (ГВЗ) в области рабочего телесного угла диаграммы направленности (ДН) навигационной антенны [3]. ГВЗ и ЛФЦ взаимосвязаны и могут быть определены на основе известной, рассчитанной или измеренной, фазовой диаграммы (ФД), при этом для определения ГВЗ необходимо знать частотную зависимость изменения фазы антенны или ее ЛФЦ для каждого из интересующих направлений.

Фазовый центр (ФЦ) антенны является точкой пространства, относительно которой фаза излученного или принятого сигнала в дальней зоне постоянна на сфере с центром в этой точке [4]. Положение ФЦ для любой антенны зависит от частоты сигнала и величины сектора углов, в котором определена его ФД [5].

Любой источник излучения конечного размера, которым и является антенна, будет генерировать эквифазные контуры, не являющиеся в полной мере сферическими и имеющие отклонения фазы сигнала в зависимости от направления наблюдения. В данном случае мы увидим небольшие, близкие к сферическим, участки волнового фронта с соответствующим центром для каждого участка. Единого фазового центра, иногда называемого интегральным или эффективным, являющегося ФЦ для полного телесного угла в 4π стерадиан, не существует или он может быть ²⁸⁰ определен приблизительно, с ограничениями по точности.

Радиотехнические характеристики, в том числе и фазовые, бортовой фазированной антенной решетки (ФАР) космического аппарата (КА) «Глонасс» определяются количеством излучающих элементов, их амплитудно-фазовым распределением и расположением относительно друг друга. Немаловажную роль при этом играет и расположение ФАР на КА, возможное окружение другими антеннами и элементами конструкции, расположенных в непосредственной от нее близости на сотопанели КА.

Поскольку фазовый центр антенны спутника не является точкой, максимально точно описывающей движение спутника по орбите, осуществляют его привязку к центру масс КА. Сама навигационная антенна для удобства этой привязки располагается как можно ближе к центру базовой системы координат КА.

Исследования, посвященные поиску эффективного фазового центра спиральных излучателей при использовании их как в качестве одиночной антенны, так и в качестве облучателя зеркальной антенны [6], дают ряд выражений, определяющих зависимость ФЦ от геометрических размеров такой антенны и позволяющих с некоторой степенью достоверности использовать его положение в дальнейшем. В общеупотребимом смысле счи-

Том 6

тается, что в качестве отправной точки для поиска ФЦ спиральной антенны на практике за его положение принимается расстояние, равное 1/3 высоты спирального проводника от ее экрана. Такое упрощение применимо лишь только при измерениях коэффициента усиления исследуемой антенны и едва ли приемлемо для решения задач навигации и геодезии.

Как отмечалось ранее, радиотехнические характеристики навигационной ФАР определяются свойствами ее излучающих элементов, их парциальных ДН и индивидуальными ФД с учетом их взаимного влияния. Для полноценной оценки ЛФЦ навигационной ФАР с учетом все более возрастающих требований по точности его определения крайне важно знать положение ЛФЦ излучателя и его смещения в пространстве при изменении направления наблюдения. Подобную зависимость принято называть годографом ЛФЦ [2].

В настоящей статье рассмотрены вопросы, посвященные анализу фазовых характеристик одиночного спирального излучателя навигационной ФАР, нахождению пределов перемещения координат его ЛФЦ в заданном телесном угле или рабочей области ДН.

1.    Методика расчета ЛФЦ излучателя навигационной ФАР

Рабочий диапазон частот навигационной ФАР представлен тремя поддиапазонами частот, называемыми L1, L2 и L3, при этом используются схемы с частотным и кодовым разделением сигналов [7]. Диапазон L3 в бортовой навигационной антенне используется сравнительно недавно на КА нового поколения «Глонасс-К1» и «Глонасс-К2».

Для анализа излучателя ФАР, используя пакет электродинамического моделирования CST MWS, была построена его точная модель с учетом всех конструктивных особенностей и входящих мате-

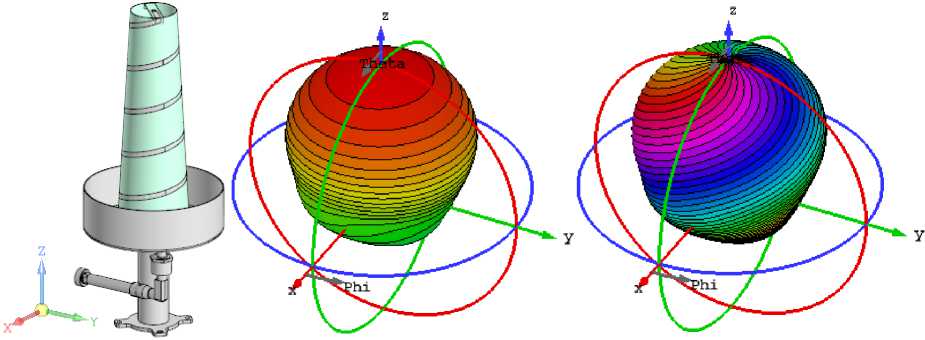
Рис. 1. Внешний вид излучателя ФАР, его амплитудная и фазовая диаграммы направленности

риалов. Расчет проводился относительно посадочной плоскости антенны, совпадающей с фланцем кронштейна излучателя. Внешний вид спирального излучателя и его расчетные амплитудная и фазовая диаграммы в сферической системе координат на центральной частоте диапазона L3 представлены на рис. 1. Поляризация формируемого электромагнитного поля близка к круговой правой стороны вращения и определяется правовинтовой намоткой спирального проводника [8].

Анализируя полученные данные, можно сказать о достаточно хорошей симметрии ДН, небольшое отклонение ее электрической оси вызвано несимметричной запиткой спирали излучателя. Характер фазового фронта, представленный на рис. 1, определяется тем, что в сферической системе координат (ССК) в ДН спирального излучателя F (6 , ф) = А( 6) • (6 + / ф) • е ^Уф имеется фазовый сомножитель e ^{jm ϕ} , обусловленный вращением ее ортов по ф. Т. е. имеет место, так называемая, первая вариация фазы ( m = 1).

Чтобы избежать неопределенности в ориентации ортов ССК и неравномерности координатной сетки в приполярной области целесообразно анализ фазового фронта (ФФ) проводить вблизи экваториальной области, где координатная сетка ССК равномерна и ориентация ее ортов достаточно стабильна. Такой переход, по нашему мнению, можно сделать несколькими способами: расчет характеристик излучателя проводить при его ориентации по оси OX ССК, а не по оси OZ; трансляция осей ССК после расчета средствами CST MWS; использование системы координат (СК) Ludwig2 [9; 10], реализованное в этом программном пакете.

Стоит отметить, что независимо от того какой способ применяется, полученные преобразованные ФД, их внешний вид и кривизна, а также ²⁸¹ значения фазы не отличаются. Небольшие отклонения возможны только при изменении ориентации облучателя по причине изменения сетки разбиений исследуемой модели, что может быть нивелировано ее увеличением до приемлемого уровня с точки зрения необходимой точности решаемой задачи.

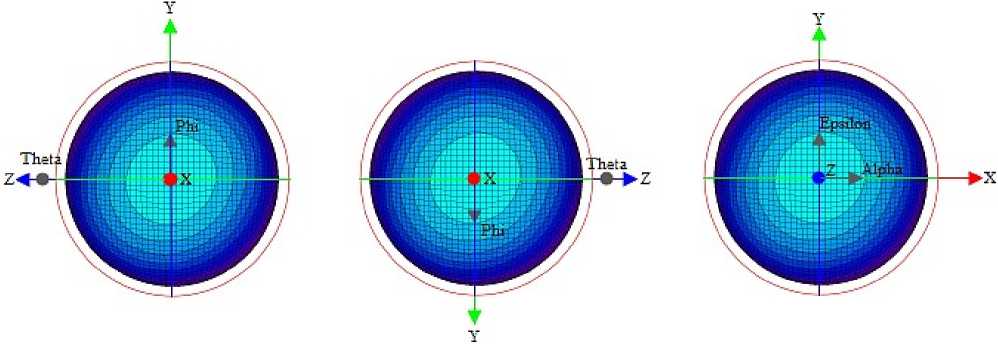
На рис. 2 приведены для сравнения ФД и ориентация ортов их СК для трех вышеприведенных случаев. Ориентация осей, перпендикулярных оси, совпадающей с направлением конуса излучателя, подобрана так, чтобы обеспечить

аб   в

Рис. 2. К способу представления ФД: а – ФФ при ориентации излучателя по оси ОХ ; б – ФФ при трансляции осей ССК; в – ФФ в СК Ludwig2

представление в едином формате для сравнения и большей наглядности.

Очевидно, что все представленные ФД могут быть, в равной степени, использованы для дальнейших вычислений, а отличие, порождаемое вращением осей систем координат, проявляется лишь в разнице знаков углов, соответствующих направлениям θ, φ и ε, α.

Для проведения расчета ЛФЦ выберем область анализа из имеющейся ФД в диапазоне ±30° по обеим угловым координатам. Для случая, приведенного на рис. 2а, это соответствует диапазону углов от 60° до 120° по углу θ и от –30° до +30° по углу φ. Полученный сегмент ФД, представленный сеткой, близкой к прямоугольной, с выбранным угловым шагом между ее узлами, подлежит дальнейшему анализу.

В соответствии с [2; 5] координаты ЛФЦ ( X , Y , Z) определяются как центр участка сферической поверхности, которая в среднеквадратичном смысле аппроксимирует участок поверхности ФФ в пределах малого телесного угла вблизи точки наблюдения. Расчет интересующих нас координат ЛФЦ сводится к решению системы линейных алгебраических уравнений (1) для набора точек в выбранном телесном угле с центральной точкой, соответствующей конкретному направлению (θ, φ):

Том 6

E (csn )2 • X + Е (csn • ssn ) • Y + Е (csn • cn ) • Z + E (csn ) • Rсф = E(Rn • csn X nn    n    nn

E(csn • ssn)• X + E(ssn)2 • Y + E(ssn • Cn)• Z + E(ssn)'RсФ =E(Rn • ssnX n     nn    nn

E(csn • Cn)• X + E(ssn • Cn)• Y + E(Cn)2 • Z + E(Cn)• Rсф =E(Rn • Cn), n     n    nnn

E ( CS n ) • X + E ( ss n ) • Y + E ( C n ) • Z + n • R сф = E ( R n ), nnnn

где cs n = cos(ф n ) • sin(9 n ), ss n = sin(ф n ) • sin(9 n ), ^cn = ^cos( ⁹ n X R „ = R o +V ( ⁹ n , Ф n )/ k . При этом v(⁹ n , ф п ) и k представляют собой значение фазы поля и волновое число соответственно, а R ₀ – расстояние, для которого проводился расчет поля излучателя в дальней зоне.

Число используемых в расчетах ЛФЦ точек следует определять с учетом кривизны имеющего место ФФ конкретной антенны, но не менее четырех. Для анализа перемещения ЛФЦ излучателя навигационной ФАР авторы использовали различное количество выборки точек от 4 до 9 вокруг центральной ( n = 4^9) с шагом 2 ° по обоим углам. Ввиду незначительного отличия в полученных результатах и с учетом формы ФФ, представленного ранее (рис. 2), в данной работе будут приведены результаты вычислений ЛФЦ для девяти точек.

2.    3D годограф ЛФЦ излучателя навигационной ФАР

Поиск ЛФЦ проводился в секторе углов ФД ±30°, рассчитанной с шагом 2° по обеим координатам 9 и ф, на центральных частотах диапазонов L1, L2 и L3. Алгоритм вычисления ЛФЦ, описанный выше, был организован в среде Mathcad в виде подпрограммы-функции, вызываемой для каждого направления (9 ij , ф^), где i и j - индексы узлов сетки координат для центральной точки. В расчетах шаг этой сетки также был выбран равным 2°.

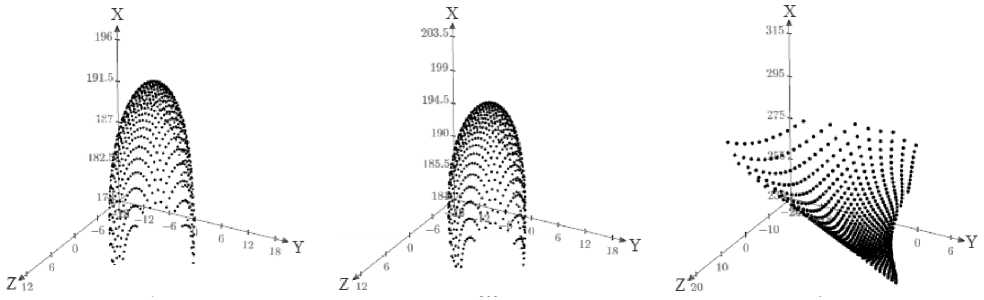
Результаты расчета ЛФЦ приведены на рис. 3 для каждой из частот соответственно. Представлены точки ЛФЦ, соответствующие коническому телесному углу рабочей области направлений: (92 + ф2)1/2 < 30°.

б

а

в

Рис. 3. 3D годографы ЛФЦ: а – для частоты 1202 МГц диапазона L3;

б – для частоты 1246,5 МГц диапазона L2; в – для частоты 1602,5 МГц диапазона L1

Для удобства восприятия результаты расчета ЛФЦ, показанные на рисунках выше, сведены в таблицу, где представлены их предельные отклонения от геометрической оси излучателя по каждой из координат.

Распределение ЛФЦ и пределы их перемещений для частот диапазонов L2 и L3 носит схожий характер, что обусловлено близостью этих частот. Кроме того, поверхность, описывающая перемещение ЛФЦ, является равномерно убывающей при отклонении области анализа от геометрической оси излучателя, ввиду лучшей симметрии амплитудной (АДН) и фазовой (ФДН) диаграмм излучателя на этих частотах.

Перемещение ЛФЦ для частоты диапазона L1 носит иной характер. Имеется значительное поперечное смещение ЛФЦ по осям Y, Z с различными комбинациями знаков при равномерно растущей или убывающей по X координате, что приводит к причудливому распределению координат ЛФЦ и к не менее своеобразной поверхности.

Очевидное отличие результатов расчетов для разных диапазонов излучателя может быть характеризовано их амплитудными и фазовыми диаграммами и отличиями между ними. В соответствии с представленными АДН и ФДН на рис. 4 можно видеть, что для диапазонов частот L2 и L3 геометрическая ось излучателя наиболее точно совпадает с направлениями их максимумов, а для частоты диапазона L1 имеется заметное отклонение по АДН и ФДН в сторону одной из четвертей диаграмм.

Таблица

Расчетные изменения положения ЛФЦ

L3, 1202 МГц	θ = 90°, φ = 0° (ось ФД)	Максимальные положительные уходы ЛФЦ	∆max, мм	Максимальные отрицательные уходы ЛФЦ	∆min, мм	|∆|		283
X , мм	195,475	195,552	0,077	178,071	–17,404	17,404
Y , мм	–0,017	12,205	12,222	–12,392	–12,375	12,375
Z , мм	0,409	11,575	11,166	–10,52	–10,929	11,166
L2, 1246,5 МГц	θ = 90°, φ = 0° (ось ФД)	Максимальные положительные уходы ЛФЦ	∆max, мм	Максимальные отрицательные уходы ЛФЦ	∆min, мм	|∆|
X , мм	200,164	200,201	0,037	181,477	–18,687	18,687
Y , мм	0,082	12,016	11,934	–12,035	–12,117	12,117
Z , мм	0,737	11,661	10,924	–9,978	–10,715	10,924
L1, 1602,5 МГц	θ = 90°, φ = 0° (ось ФД)	Максимальные положительные уходы ЛФЦ	∆max, мм	Максимальные отрицательные уходы ЛФЦ	∆min, мм	|∆|
X , мм	247,922	310,337	62,415	237,279	–10,643	62,415
Y , мм	–3,206	5,495	8,701	–18,366	–15,16	15,16
Z , мм	0,795	18,177	17,382	10,614	11,409	17,382

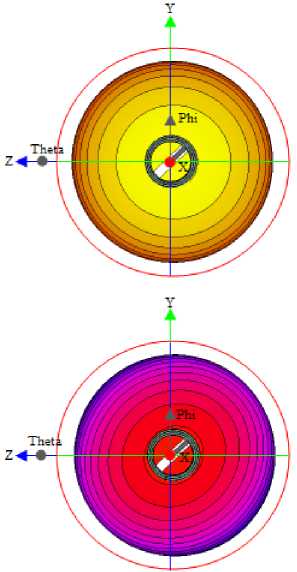
а

Рис. 4. Характер АДН и ФДН: а – на частоте диапазона L3; б – на частоте диапазона L1

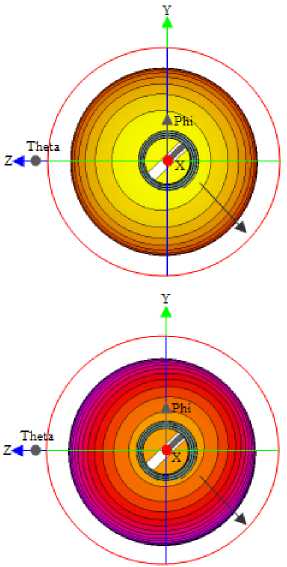
б

Изменение значений фазы для частоты L3 при ф = const = 0° и 9 = const = 90° в пределах углов проводимого анализа составляет практически одинаковые значения 37,3° и 37,57°. Данный факт говорит о достаточно хорошей симметрии ФДН, при этом форма ФФ представляет собой слабо вы-

(шмчесЬё

АППАРАТЫ И

раженный эллипс, имеющий наклон относительно осей Oy и Oz , близкий к 45°. Для частоты L1 изменение фазы в двух ортогональных сечениях лежит в диапазоне 63,56° – 66,6° и 69,39° – 60,9° соответственно. Для сечения ФДН, ориентированного по малой оси эллипса ФФ, эта разница еще более выражена. Такое смещение АДН и ФДН вызвано, в том числе, большим влиянием асимметрии точки запитки спирального проводника на более высоких частотах.

Для оценки пределов перемещений ЛФЦ излучателя

²⁸⁴ глядности годографы бражения,

навигационной ФАР и большей на-совместим ранее представленные ЛФЦ с его моделью. Такие изо-представленные на рис. 5 и 6, це- лесообразно сделать только для частот L3 и L1, ввиду их отличия, исключив распределение для частоты L2, схожего с таковым для L3.

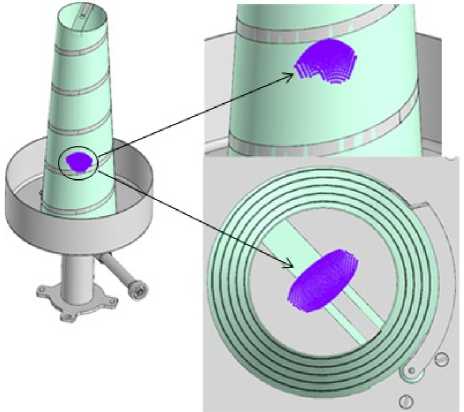
Рис. 5. 3D годограф ЛФЦ излучателя ФАР на частоте L3

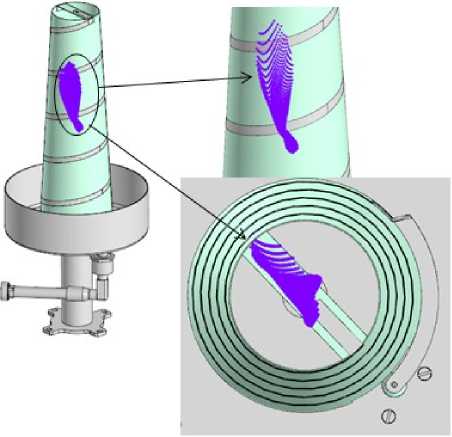
Рис. 6. 3D годограф ЛФЦ излучателя ФАР на частоте L1

Том 6

Ранее описанная особенность характера перемещений ЛФЦ для частот диапазона L1 при использовании излучателя в составе ФАР приведет к меньшему влиянию на ее фазовые характеристики, поскольку при формировании так называемой равносигнальной ДН в качестве центрального кластера используются четыре аналогичных излучателя. С учетом того, что они развернуты относительно друг друга на 90° вокруг своей оси и синфазны в дальней зоне, будет сформирована более равномерная как амплитудная, так и фазовая диаграммы кластера излучателей во всех частотных диапазонах.

Заключение

В настоящей работе рассмотрена методика и особенности расчета годографов ЛФЦ одиночного излучателя навигационной ФАР КА «Глонасс» с учетом присущих ему фазовых характеристик в диапазонах частот L1, L2 и L3.

Проведенные расчеты показали существенное отличие пределов перемещений ЛФЦ излучателя, ввиду значительного отличия его ФФ, формируемого на частотах L2, L3 и L1. Поэтому при проведении подобного рода оценки даже для простой антенны, которой, несомненно, является спиральный излучатель из состава ФАР, первичным будет именно характер сформированного фазового фронта.

Тем не менее, как это представлено в данной работе, даже зная кривизну ФФ и распределение фазы в области рабочего телесного угла, невозможно прогнозировать внешний вид поверхности 3D годографа. Преобразование фазового фронта в 3D годограф ЛФЦ позволяет получить более наглядную картину фазовых свойств как одиночного излучателя, так и ФАР на его основе с учетом того, что в соответствии с технической документацией требования задаются именно к пределам перемещения ФЦ, а не к изменению значений фазы ФДН.

Ввиду того, что при проведении вычисления ЛФЦ излучателя использовалась расширенная область ФФ, составляющая ±30° по обоим направлениям углов, следует ожидать, что для рабочего сектора углов ФАР, лежащего в конусе ±19°, пределы перемещения ЛФЦ будут несколько меньше.

Кроме того, использование при проектировании ФАР равномерного разворота ее излучателей относительно друг друга нивелирует существенную неравномерность распределения ЛФЦ для всех рабочих частот и, особенно, для диапазона L1.

В дальнейших исследованиях большой интерес в равной степени будет представлять анализ перемещения ЛФЦ и его 3D годограф отдельных кластеров ФАР (центрального и периферийного), образованных четырьмя и восемью такими излучателями, а также полноценной ФАР с учетом амплитудно-фазового распределения ее диаграммообразующей схемы.