Голографические диффузоры c контролируемой индикатрисой рассеяния

Различные типы оптических элементов используются для формирования пучков света с определенной диаграммой рассеяния. Матовое стекло рассеивает свет во всех направлениях, но имеет низкую оптическую эффективность. Хотя экраны, основанные на структурах со случайной поверхностью (матовое стекло), доступны в промышленном масштабе благодаря низким ценам, область применения таких экранов очень ограничена из-за практической невозможности управлять их диффузионными характеристиками.

Для рассеяния света используются также периодические микролинзовые массивы, дифракционные элементы, голографические диффузионные экраны и т.д. [1, 2]. В [3] прозрачные анизотропные диффузоры были использованы при создании экрана 3D-дисплея. Новый класс формирователей пучка, таких как случайные микролинзовые массивы и диффузионные рельефные поверхности, имеет высокую пропускную способность, контролируемое угловое распределение и однородное распределение интенсивности света. Такие элементы не имеют дисперсионной зависимости от длины волны света и работают одинаково хорошо при освещении белым светом, монохроматическим, когерентным или некогерентным светом. При этом высокая оптическая пропускная эффективность > 90 % может быть достигнута для длин волн от 365 нм до 2000 нм. Дизайн и моделирование микро-оптических систем по-прежнему является непростой задачей, поскольку классические методы, такие как трассировка лучей, не учитывают дифракционные и другие когерентные эффекты, проявляющиеся при прохождении света через массивы микрооптических элементов. С другой стороны, существуют строгие скалярные дифракционные методы для моделирования оптических систем. Но они также ограничены в своих приложениях, потому что они либо пренебрегают непараксиальными эффектами, либо вычислительное время слишком велико для практического применения.

В настоящей работе исследуется дифракция света на диффузионных экранах, полученных голографическим методом. Получены соотношения между параметрами, определяющими функциональные особенности таких оптических элементов (дисперсия высоты шероховатости и длина корреляции). Показана возможность управления диаграммой рассеяния с помощью изменения отношения дисперсии высоты к длине корреляции шероховатости поверхности. Исследовано также влияние пространственной когерентности источника света и показателя преломления материала на характеристики рассеянного излучения.

Постановка задачи

Частично-когерентный свет описывается с помощью функции когерентности [4, 5]:

Г ( r , r ', z ) = ^Е * ( r , z ) E ( rz )У                       (1)

где Е - амплитуда электрического поля, угловые скобки обозначают усреднение по ансамблю реализаций от произведения соответствующих компонент поля.

Распределение интенсивности поля за экраном с рельефной поверхностью описывается выражением [4, 5]:

2\        ( к Л ²

I ( r , z ) = ( Е ( r , z ) = A 4 — Дг_о ( r;,r^) X \                ( 2 n z )

X (exp i [ Ф ( r ') -Ф ( r ₂ *) ]^ G *( r ', r , z ) X                (2)

xG (r2', r, z) d2 r1' d2 r2', где Г0 (r1', r2) - функция когерентности источника света в начальной плоскости, A0 - нормировочная постоянная, Ф(r) - изменение фазы, обусловленное экраном, Ф(r) = кAnh(x,y), An = n2 n 1, где n 1 - показатель преломления окружающей среды, n2 - показатель преломления экрана, h(x, y) - профиль поверхности, G(r 1, r, z) - функция Грина, r(x, y) - координата в поперечной плоскости, к - волновое число, z - продольная координата.

Излучение частично-когерентного источника света может быть описано с помощью модельного пучка Шелла – Гаусса [5, 6]

^Г ( r , r 2 ) = I 0 exP -

-

—2 —2 r + r

a 0²

-

( — - —2

² r ₀

£ - 2П. jr

%Rf' 2

-

— ²U, (3)

где a 0 – радиус пучка, r 0 – радиус когерентности, R f – радиус кривизны волнового фронта, — = ( x₁, y₁), r₂ = ( x ₂, y ₂), % - длина волны излучения.

Численный анализ дифракции света на основе уравнения (2) требует больших временных ресурсов, поэтому необходимо разработать быстрые алгоритмы для вычислений. В [2] был предложен метод, сочетающий распространение волн и процедуру трассировки лучей для анализа частично-когерентных пучков света, дифрагированных микролинзовым массивом. Это существенно ускоряет расчёты мик-рооптических систем. В [7] формализм матрицы плотности используется для рассмотрения распространения частично-когерентных световых пучков в неоднородной среде. При анализе влияния поверхностей со сложным профилем оказывается эффективным разложение поля пучка на поверхности по когерентным состояниям (КС), представляющим собой элементарные Гауссовы пучки [8]. Прохождение Гауссовых элементарных пучков (КС) через границу раздела двух сред в зависимости от угла падения определяется соответствующими коэффициентами Френеля. Обычно формулы Френеля получают для плоских волн. Однако эти формулы могут быть использованы также для локализованных волновых пучков с радиусом а о > % [9].

Для Гауссовой статистики случайной фазы Φ( r ), характеризующей форму поверхности экрана, получаем

(exP i [ ^{ф (} r i ) ^{-ф ( r} 2 )]) = ^ехр { ^-о ф [ 1 ^- У о ( ^r 2 ^- r i ) ] } , ⁽⁴⁾ где Ф( r ) = k A nh ( r ), о ф = ( k A n ) ² о 2 - дисперсия, у_ф ( ⁵ ) = (^ф( r ) ^ф ( r + ⁵ )} / о ф - коэффициент корреляции.

Рассмотрим экран, где рельеф поверхности описывается с помощью распределения высоты и автокорреляционной функции шероховатости Гауссовой формы. Такие поверхности представляют собой случайные микролинзовые массивы. Усредненные значения геометрических параметров элементов массива близки к параметрам микролинз в регулярном микролинзовом массиве [1, 10].

Для средних размеров элементов массива выполнены следующие соотношения: а ₀ >>  d >> % , где d -средний диаметр растра. Характерные геометрические размеры близки к параметрам микролинзового массива [1, 10]: d~ 20-100 мкм. Фотографии реальных профилей поверхностей голографических диффузоров приводятся, например, в [11].

Шероховатость характеризуется дисперсией о h и корреляционной длиной L c фазовых флуктуаций

(h ( r i ) h ( r , )} = o h exp ^[- ( R / L c ) ² ] , R = r i - r , . (5)

В случае падающего пучка с Гауссовым профилем распределения интенсивности и сильных флуктуаций о ф >>  1 интеграл (2) вычисляется аналитически. Показано, что контролируемый угол рассеяния можно получить путем изменения отношения дисперсии высоты шероховатости о _h к длине корреляции L c (чем меньше длина корреляции, тем больше угол расходимости). Для того чтобы получить угол рассеяния, превышающий 140°, необходимо, чтобы дисперсия высоты шероховатостей превышала корреляционную длину в 3 –4 раза. Отметим, что в случае светодиодных источников при заданной длине корреляции требуемая дисперсия высоты шероховатости уменьшается. На индикатрису рассеяния влияет также степень когерентности (радиус когерентности r 0 ) падающего пучка света.

Результаты расчетов и экспериментов

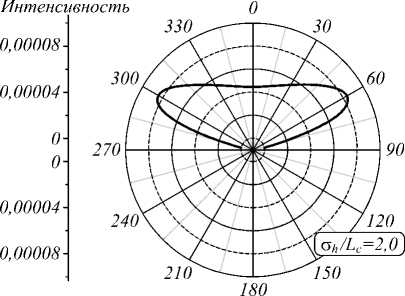
На рис. 1 представлены распределения интенсивности в поперечной плоскости z = 15 мм и индикатрисы рассеяния для различных значений отношения σ h / L c .

Мощность падающего излучения (площадь под кривой интенсивности) нормирована на единицу, поэтому максимальные значения интенсивности уменьшаются с увеличением угла расходимости. На рис. 1 в , г по оси ординат заданы значения интенсивностей на осевой линии диаграммы направленности. Из расчетов следует, что угол рассеяния увеличивается с увеличением σ h / L c . Это означает, что угол рассеяния уменьшается, когда длина корреляции L c увеличивается или когда σ h уменьшается.

В отличие от периодических микролинзовых массивов [10] неоднородности в распределении интенсивности отсутствуют.

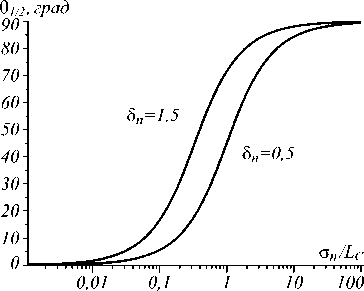
На рис. 2 приведена зависимость угла расходимости пучка от отношения дисперсии высоты шероховатости к корреляционной длине для различных значений показателя преломления материала диффузора 5 n = ( n -1). Значение угла расходимости рассчитывалось по уровню 1/ e в распределении интенсивности в поперечной плоскости. Видно, что при увеличении показателя преломления угол расходимости пучка возрастает.

На рис. 3 представлены распределения интенсивности и индикатрисы рассеяния (расчет) в случае дифракции излучения лазерного диода микролинзовым массивом и голографическим диффузором.

Как видно из рисунка, случайный микролинзовый массив (голографический диффузор) позволяет полностью устранить резкие скачки в диаграмме излучения. Отметим, что голографический диффузор является более общим случаем «случайного микролинзо-вого массива», где случайные изменения профиля поверхности коррелированы.

На рис. 4 представлены распределения интенсивности света в дальней зоне (эксперимент).

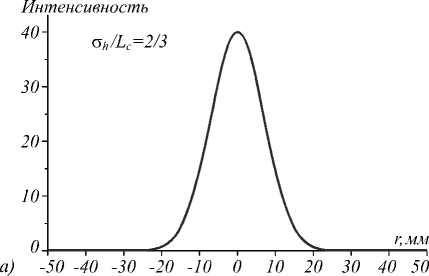
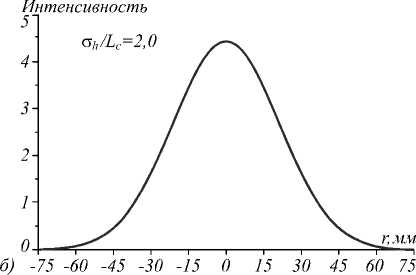
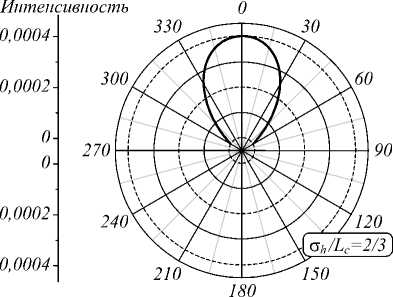
Рис. 1. Распределение интенсивности (а, б) и диаграммы рассеяния (в, г): n 2 = 1,5; λ = 630 нм

направленности. Расстояние между пятнами больше для растров с большим числом микролинз или с меньшим диаметром растра d .

Интенсивность

Рис. 2. Угол рассеяния в зависимости от σ h / L c для различных значений показателя преломления материала: n = 1,5 и n = 2,5

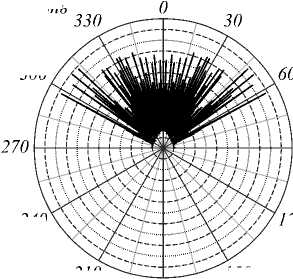
В измерениях использовались цилиндрический микролинзовый массив с диаметром растра d = 127 мкм (200 lpi) и голографический диффузор фирмы Luminit [11] с индикатрисой рассеяния 20°. Как видно из рис. 3, периодическая структура ( L c →∞ ) и голографический диффузор по-разному рассеивают падающее на них излучение. В случае периодической структуры при r 0 >>  d четко проявляется неоднородность в распределении интенсивности дифрагированного пучка (рис. 3 а и рис. 4 а ).

Отметим, что в случае двумерной периодической структуры (микролинзового массива) излучение преобразуется в двумерный (дискретный) массив пятен.

Периодическая структура расщепляет падающий пучок на множество отдельных пучков (пятен), в то время как голографический диффузор создает равномерно расширяющийся пучок с заданной диаграммой

0,0250,0200,0150,0100,005

00,0050,0100,0150,0200,025-

а)

Интенсивность 0,000123

0,00008-

0,00004-

0-

0,00004-

0,00008-

0,00012-1

б)

180 О

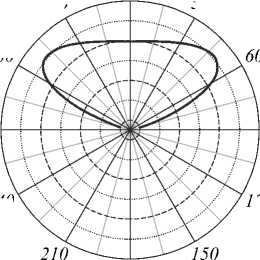
Рис. 3. Индикатрисы рассеяния в случае дифракции излучения лазерного диода с r 0 = 15 см микролинзовым массивом при z = 1,5 мм (a) и голографическим диффузором

с σ h / L c = 3/2 при z = 15 мм (б)

a)

• б)

Рис. 4. Распределения интенсивности в случае дифракции излучения лазерного диода микролинзовым массивом (а) (z = 1,45 м, расстояние между пятнами s = 7,5 мм) и голографическим диффузором (б) с полным углом рассеяния 20 ^о (z = 15 cм)

Для синтеза диффузора голографическим методом в качестве объекта голографирования можно использовать оптический рассеиватель в виде матового стекла [12, 13]. Для записи голографического диффузора облучается рассеиватель, как правило, кусок матового стекла или другого подходящего диффузора с помощью лазерного луча с длиной волны длины λ 0 и шириной D . Записываемый материал (пленка) помещается на расстоянии R от рассеивателя и подвергается воздействию лазерной спекл-картины. Средний размер регистрируемых спеклов ~ λ 0 R / D определяет величину углового расхождения света при подсветке экспонированной спекл-структуры (голографического диффузора) – чем меньше размер спекла, тем шире угловое расхождение рассеянного пучка. Длина корреляции L c определяется спекл-структурой лазерного излучения, которая записывается на фоторезисте или пленке.

Отметим, что рассматриваемые голографические диффузоры обладают оптической эффективностью > 85 % [11]. Эффективность же матовых стекол в видимом диапазоне обычно меньше 35 %.

Для получения однородного распределения интенсивности света после прохождения микролинзово-го массива в системах подсветки дисплеев обычно используются источники с низкой когерентностью (светодиодные излучатели). Однако для повышения яркости и контрастности изображений лучше подхо- дят лазерные источники излучения. В настоящей работе показано, что при использовании голографических диффузоров возможно получение однородного распределения интенсивности и при работе с когерентными источниками излучения.

Заключение

Таким образом, в работе исследована дифракция света на диффузионных экранах, полученных голографическим методом. Такие экраны представляют собой случайный микролинзовый массив, профиль поверхности которого описывается дополнительным параметром, задающим статистические свойства флуктуации высоты – длиной корреляции. Показано, что индикатриса рассеяния сужается с увеличением длины корреляции неоднородностей L c . Получено, что при увеличении показателя преломления материала диффузора угол расходимости пучка возрастает. Голографические диффузоры могут быть использованы в 3D-дисплеях [14] для повышения яркости изображения и создания однородных зон просмотра.

Полученные результаты представляют практический интерес и могут быть использованы в системах подсветки различных экранов дисплеев, а также при разработке новых оптических элементов для формирования пучков света с заданной угловой расходимостью.

Работа выполнена при поддержке гранта Российского научного фонда (проект № 17-19-01461).