Гомотопические снопы расслоений

1.    Введение1.1.    Скручивания топологической К-теории

Комплексная К-теория — это 2-периодическая обобщенная теория когомологий, представляемая Р-спектром { К_п } _п> о , где

К = |

Z х BU, если п четно;

U,       если п нечетно.

Таким образом, К о — В^-кольцевое пространство, и соответствующее пространство единиц есть Z/2Z х BU®. Скручивания К(X ) (где X — компактное пространство) классифицируются гомотопическими классами отображений:

X ш B(Z/2Z х BU₀) - K(Z/2Z, 1) х BBU®.

Ввиду изоморфизма спектров BUy = K(Z, 2) х BSU® [5,9] скручивания классифицируются элементами группы Н ¹(Z/2Z, 1) х Н ³(X, Z) х [X, BBSU®].

Скручивания, отвечающие первым двум множителям Н 1(Z/2Z, 1) х Н ³(X, Z), изучались М. Каруби [4], П. Донованом и М. Каруби [3], а также Дж. Розенбергом [8] в случае элементов конечного порядка и М. Атиа и Г. Сигалом [1] в общем случае. Наша цель — развить геометрический подход к скрученной К-теории, отвечающей элементам конечного порядка, из Н ³(X, Z) х [X, BBSU®].

Эта. задача, распадается на. две части: во-первых, дать геометрическое определение скручивающим коциклам и, во-вторых, определить соответствующую скрученную К-теорию и проверить выполнение необходимых свойств. Данная работа, посвящена, первой части этой программы — геометрическому определению скручивающих коциклов, роль которых играют так называемые «гомотопические снопы расслоений».

Последнее понятие родственно понятию снопа расслоений, введенному в работе [6]. Сноп расслоений можно рассматривать как геометрическое представление элемента из Н ³(X, Z) (соответствие задается классом Диксмье—Дуади), подобно тому как комплексное линейное расслоение дает геометрическое представление элемента Н ²(X, Z) (соответствие задается первым классом Чженя). Для скручивания конечного порядка а Е Н ³(X, Z) соответствующая К-теория может быть определена следующим образом: выбирается сноп расслоений (L, Y ) с классом Диксмье—Дуади, равным а, и затем рассматривается симметризация коммутативного моноида, состоящего из классов изоморфизма, конечномерных модулей над данным снопом с операцией прямой суммы [2].

1.2.    Проективные коциклы и снопы расслоений

Конструкции и результаты о гомотопических коциклах и гомотопических снопах расслоений, излагаемые в следующих разделах, во многом аналогичны теории проективных коциклов и «обычных» снопов расслоений, которую мы кратко напоминаем ниже в удобной для нас форме. Подробности см. в [2,6,7].

Зафиксируем некоторое положительное число к > 1 и рассмотрим проективную унитарную группу PU(k) := U(k)/U(1) — фактор-группу U(k) по центру. Пусть

Рк 1 = U(k) х C ^ PU(k)(2)

’

• —    каноническое линейное расслоение над PU(k), ассоциированное с главным U(1)-расслоением

U(1) ^ U(k) ^ PU(k).(3)

Эти данные определяют некоторый сноп расслоений (L(g), У ), где линейные расслоения L_ap := g*^Рк, 1 ^ U_ap определены как обратные образы канонического линейного расслоения Рк, 1, причем произведение

~

ӨаР^і ^{: L}ctJ3 ^{0 L}P7 ^ ^L*7

над тройными пересечениями U*^ определяется с помощью группового умножения

Ц к : U(k) х U(k) ^ U(k)

(ср.(3)). В частности,

Ц к (Рк, 1 ) = Рк, 1 ИРк, 1 ,                                          (4)

где цк : PU(k) х PU(k) ^ PU(k)

• —    умножение в группе и И обозначает внешнее тензорное произведение. Очевидно, произведение Ө ассоциативно над четырехкратными пересечениями, то есть диаграммы

^ а (3^ ® id L,^ ^

L*g 0 Lg₇ 0 L₇5--->■ L*₇ 0 L75

id L_ap ®⁹P^S

Y

LaP 0 LPS--у--

УаР5

Өа^§

LaS

коммутативны над U_ap76.

Сноп (L(g), У ) имеет характеристический класс со 'значениями в Н ³(X, Z) (причем его порядок делит к) — класс Диксмье—Дуади; напомним его конструкцию. Так как U — хорошее покрытие, то можно выбрать сечения ст*р эрмитовых линейных расслоений L*p ^ U*_p. равные по модулю единице в каждом слое. Тогда над U_ay₇ имеем

Өа^7(^аД 0 00) — АаД7^«7

для некоторых функций А*^: U*^₇ 0 U(1) и, используя условие ассоциативности (5), получаем, что А = {А*ю} — 2-котщк.т Чеха с коэффициентами в U(1) — пучке ростков U(1)-3Ha4Hbix непрерывных функций. Используя кограничный гомоморфизм

• 5 : Н ²(X, U(1)) ^ Н ³(X, Z)

(являющийся изоморфизмом, так как R — тонкий пучок, и, значит, Н ^:(X, R) = 0 для і > 1) в длинной точной последовательности когомологий, ассоциированной с короткой точной последовательностью пучков

0 s Z s r ‘"-s'"’ U(1) s 1, определяем класс Диксмье—Дуади DD(L(g) У) как 5([А]), где [A] G Н2(X, U(1)) — класс когомологий коцикла А. Этот класс — препятствие (причем единственное) к существованию подъема проективного коцикла {дар} до и(к)-коцикла. Снопы расслоений с одним и тем же классом Диксмье—Дуади называются стабильно эквивалентными.

По Ри(^)-коциклу {д_ар } строится главное PU(k)-paccnoeние над X, и таким образом получается взаимно однозначное соответствие между множеством Н ¹ (X, PU(k)) и множеством классов изоморфизма главных Ри(^)-расслоений с базой X. Существует гомотопическое описание последнего множества: каждое главное Ри(^)-расслоение над X классифицируется некоторым отображением X s BPU(k), единственным с точностью до гомотопии, то есть существует естественная по X и PU(k) биекция множеств Н 1(X, PU(k)) = [X, BPU(k)], где [X, У] обозначает множество гомотопических классов отображений X s У.

Мы также имеем точную последовательность пучков

1 s U(1) s U(k ) s PU(k) s 1,                         (6)

отвечающую точной последовательности групп (3), и соответствующий кограничный гомоморфизм 5k : Н ¹(X, PU(k)) s Н ²(X, U(1)). Нетрудно показать, что каэюдый элемент конечного порядка в Н ²(X, U(1)) = Н ³(X, Z) принадлежаum образу 5k для некоторого к. Другими словами, произвольный сноп расслоений с классом Диксмье—Дуади конечного порядка стабильно эквивалентен некоторому снопу, полученному применением приведенной выше конструкции к некоторому проективному коциклу. Из точности последовательности когомологий, связанной с последовательностью (6), также следует, что сноп (L(g), У ) стабильно тривиален тогда и только тогда, когда соответствующий проективный коцикл g является образом унитарного коцикла при гомоморфизме Н ¹ (X, U(k)) s Н ¹ (X, PU(k)), или, на языке классифицирующих пространств, когда классифицирующее отображение X s BPU(k) для соответствующего главного PU(k)-paccnoennH поднимается до некоторого отображения X s BU(k) в расслоении

CP~ ---„ BU(k)---^ BPU(k).                         ( 7)

2.    Топологический моноид Frk/^j^

Заметим, что в приведенной в предыдущем параграфе конструкции снопов расслоений с помощью проективных коциклов использовался тот факт, что группы PU(k) являются базами нетривиальных линейных расслоений дк, i (можно показать, что любое линейное расслоение над X, имеющее конечный порядок в группе Pic(X ) = Н ¹ (X, U(1)) = Н ²(X, Z), является обратным образом дк, i для некоторого к), причем имеет место изоморфизм (4). Мы хотим показать, что данную конструкцию можно существенно обобщить, заменив группу PU(k) на некоторый топологический моноид Егк/^,/^.

2.1.    Пространства унитальных гомоморфизмов матричных алгебр

Зафиксируем пару натуральных чисел {к, 1}. Пусть Егк/т,/п обозначает пространство унитальных *-гомоморфизмов матричных алгебр Hom_tt/_g (Мк/т (C), М_ыт+п (C)). Напомним, что группа *-автоморфизмов комплексной матричной алгебры M_n (C) есть PU(n), поэтому на Fr к[т,[п определены левое действие группы PU(kl^m+n ) и правое действие группы PU(kl^m ). Более того, Frk/m,/п является однородным пространством группы PU(kl^m+n).

Предложение 1. Существует изоморфизм однородных пространств

Fr^n — PU(kl^{m + n})/(E_klm 0 PU(lⁿ)),                      (8)

где E_n обозначает единичную матрицу, а «0» — кронекеровское произведение матриц.

Доказательство является простым следствием теоремы Нетер—Сколема. □

В частности, при l — 1 имеем Frki m in — PU(fc).

2.2.    Канонические векторные расслоения над пространствами Frklm,l.

Заметим, что в представлении (8) пространства Frkim in как однородного пространства проективные унитарные группы можно заменить на унитарные:

Frkim ,ln — U(kl^{m + n} )/(Eklm 0 U(l")).                            (9)

Из этого представления вытекает, что Frkim,i” является базой главного U(ln)-paccnoeHHH

U(ln)----^U(fclm+")----*Frkim,in .                             (10)

Пуств

Д^Дп = U(fel^m+") X С” ^ Frkim,in

U(ln)

• — векторное С^-расслоение, ассоциированнoe с (10). В частности, для l — 1 мы возвращаемся к линейному расслоению +, ₁ ^ PU(fc) (ср. (2)).

Имеет место изоморфизм M_m(M_n(C)') — M_mn(C"). Сопоставление гомоморфизму

Һ : M_klm (С) ^ M_kim ₊ n (С) гомоморфизма

Mi (h):Mi(Mkim (С)) ^ Mi(Mkim+n (С)) определяет вложение

Lm +1 ,n ^{: Fr}ki^m,iⁿ ^ ^Frki^m+¹,iⁿ .

Сопоставление гомоморфизму

Һ : M_kim (С) ^ M_kim+n (С)

его композиции с

г: Mkim+n(С) ^ Mkim+n+i (С), г(Т) — El 0 Т определяет вложение

^m, п+1 ^{: Fr}ki^m,iⁿ ^ ^Frki^m,iⁿ⁺¹.

Предложение 2. Имеем

Lm+1,n(^kim+1,i" ) — ^klm,ln ,   ^m,n+1(^kim,i' 1 ) — ^klm,ln 0 rl где [l] обозначает тривиальное С+асслоеіше.

Доказательство тривиально. □

Операция композиции унитальных *-гомоморфизмов матричных алгебр определяет отображение

P-^r : Homaig (Mkim+n (С), Mkim+n+^ (С)) X Homaig (Mkim (С), Mkim+n (С)) ^ ^ Homaig (Mkim (С), Mkim+n+r (С)), то есть

^^m,r ^{: Fr} kl^m+n, i^{r X Fr} kl^m,lⁿ ^ ^Frki^m,i^n+r.

(И)

Предложение 3. В предыдущих обозначениях имеем (ср. (4)): ⁽ ^^m,r ) ⁽^kl^m,l^n+r ) ^— ^kl^m+n,l^r ^ ^kl^m,lⁿ .

Доказательство тривиально. □

2.3. Топологический моноид Ғгк/о,/о

Используя пространства Егк/т,/п и вложения L_m +i ,_n , L_m,n +1 , m, п Е N, мы можем образовать прямой предел Ег_к /о /о := lim   Ег_к/т /п. Введенные в предыдущем пункте отоб-

^m, п ражения p^r задают на пространстве Ег^/^,/^ структуру топологического моноида.

Далее мы предположим, что (к, Г) = 1. Данное условие обеспечивает нестягиваемость Ег^/^,/^: можно показать, что при этом условии

^г ^(Ег к/°,/° ) =

J Z/kZ, I0,

если г почетно:

если г четно.

Более того, его гомотопический тип не зависит от выбора Г >  1, (к, Г) = 1. В частности, лд(Ег^/^,/^) = 0, и, значит, моноид группоподобен. Кроме того, он имеет структуру CW-комплекса, а значит, вложение единичного элемента является корасслоением.

Моноид Ег^/^,/^ имеет фильтрацию

РЕ(кГ) = Ег_ы~, 1 ^ Е        - Ег_к1~_рп     ...

Замечание 1. Моноид Ег_к/о,/о удобно представлять как бесконечный телескоп, то есть ^

Ц (Егк/-щп X I)/ ~ , г=0

где I := [0, 1], по отношению эквивалентности (һ, 1) ~ ( і_гп,_п(һ), 0), г де һ Е Егкоргп.

Умножение в Егк/о,/о индуцирует отображения (ср. (11))

рп,п ^:= Р^,Т1 ^{: Ег}к/^,/^{п X Ег}к/^,/^п ^ ^Егк/^,/^2п.

Заметим, что Ег_ко/п является базой векторного С^/п-расслоения ^к/^,/п, чье ограничение на подпространство Егк/т,/п С Егк/ОО /п есть ^к/т /п (ср. Предложение 2). Более того (ср. Предложение 3),

Р-тцп^кГ^рп ) = ^к/°,/" ^ ^к/° ,/^п .                             (12)

Мы также имеем изоморфизм (ср. Предложение 2)

0,/Л^к/0,/2") = Фл0,/" 0 [Г'].                                   (13)

Таким образом, умножение в моноиде Егк/о,/о отвечает тензорному произведению векторных расслоений подобно тому, как умножение в проективной унитарной группе отвечает тензорному произведению линейных расслоений (см. (4)). Посмотрим теперь, каким будет аналог снопов расслоений в данном случае.

3.    Гомотопические снопы расслоений3.1.    Гомотопические коциклы

В случае группоподобного топологического моноида M роль 1-коциклов играют гомотопические коцикли (которые мы будем называть НТС от англ. «Homotopy Transition Cocycle»), основные свойства которых изучены в работе [10]. Так же, как в случае групп и «обычных» 1-коциклов, их (подходящим образом определенные) классы эквивалентности находятся во взаимно однозначном соответствии с гомотопическими классами отображений в классифицирующее пространство BM моноида M. Далее мы рассматриваем случай M = Егк/о,/о. Как раньше. Uc^...^ :=U_ao П ... П U^-

Определение 1. Гомотопический коцикл (д, U ) со значениями в моноиде Егк/о,/о — набор отображений

• ^дао...ат ^{: и}«0...«т ^{X 1 m 1} ^ ^Егк/°,/° ,

заданных для всех т > 1, которые согласованы в следующем смысле: если ст = («о ... «_т), ^г = («о ... «г... «_т) и (е, г)(1 ^{т -} 1 ) — г рань ti = е (е = 0 или 1), то для г = 1,... , т — 1

Если расшифровать приведенное определение, то, во-первых, мы имеем набор отображений 9_ар : U_ap ^ Егыо,/о, затем гомотопий 9_ад₇: U_a3₇ х I ^ Егы<о,/<о между 9^3 93₇ и 9^7, а также гомотопий 9^375 : U_ap^s х 1 ² ^ Ег//о,/о, которые заполняют квадрат

9а^^9^5

9а3 937 9^5---^ 9а^9^5

9^^9 ^^8

⁹“^{3 935}  9agS

9ауё ,

I

9а5,

и т.д. до бесконечности.

Без потери общности можно предположить, что 9^3 : U_a3 ^ Ег//о,/п с Ег//о,/о для некоторого п (одновременно для всех элементов покрытия), и вообще

Для тройных пересечений определим отображения 9^393^ : U^37 ^ ЕіЫод2п, заданные как композиции diag                 9«3 ^99^Л","

Ua3^ ^ Ua3^ х Ua3^  > Ег//°,/" х Ег//°,/" ^ Ег//о,/2п.(14)

Тогда над тройными пересечениями мы имеем гомотопии 9^37: U_ap^ х I ^ Ег_ы<о /2п, такие что

9«37\иар^ х{0} = 9«3937, 9«37\иар^ х{1} = ^п,п о 9«7,(16)

где L_n, _п : Ег//ос /п ^ Ег//о /2п — вложение. Заметим, что отображения і_п,_п о 9^7 и 9^7 отождествляются как отображения U_a^ ^ Ег//о,/о (ср. Замечание 1).

Над четырехкратными пересечениями U_ap^5 мы получаем диаграмму из гомотопий:

9«39 379^5

9»3^9^8

(Ы, п

о 9^7 )9^6 = 1 2 п.

п ^о(⁹«7 ⁹^5 )

⁹^Д ⁹^^8

I

^2п, п°9^75

⁹«3 ⁽ ^п,п ^{о 9}35) — ^2п, п ^о (⁹«3⁹35 )_t2n „09^^82п,п ^о ^п,п ^{о 9}«5 — ^п, 2п ^{о 9}«5,

где 1п, 2 п ^{: Ег}//оо /п ^ Ег//о /зп и т.п., которая получается из рассмотрения коммутативной диаграммы:

Лп, "Xid                            1п, п X id

Ег//о,/п х Ег//о,/п х Ег//о,/п ----^Ег//о,/2п х Ег//о,/п -s---- Ег//о,/п х Ег//о,/п

idx Цп, п

Лп, 2"

Ег//°,/п х Ег//о,/2п ---------

idX I", п

Ег//о,/п х Ег//о,/п--------

Ег

Ег

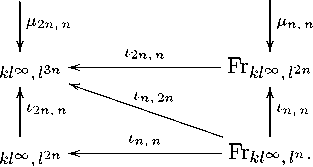
Следующее условие гомотопического коцикла состоит в том, что существует гомотопия ⁹«3^5 ^{: U}^3^5 ^{х 1} 2 ^ ^Ег//^о,/^3п ,

такая что

⁹«375\ц_а^₇₅ х/х{0} = ⁹«37⁹75\^_a^₇j xl,   ⁹а3у5 \ц_а^₇₅ x/x{1} = ^2п, п ^{о 9}«35\^^₂,_Л х1,

⁹«375\ц_а^₇₅х{0}х/ = ⁹«3⁹375\^_а^₇й xl,   ⁹«375\^_а^₇₈х{1}х/ = ^2п,п ^{о 9}«75\^^_2лЛ xl^.

Далее мы имеем гомотопии над пятикратными пересечениями и т.д.

Посмотрим теперь, к какому аналогу понятия снопа расслоений приводят гомотопические коциклы.

3.2.    Гомотопические снопы расслоений

В начале работы мы видели, что снопы расслоений естественно возникают из проективных коциклов. Рассматривая НТС (д, U ) как аналог проективного коцикла, можно определить понятие гомотопического снопа расслоений (HBG, от англ. Homotopy Bundle Gerbe) (£(д), У), рассматривая обратные образы канонического расслоения над моноидом.

Выше были определены канонические векторные С’Арасслоения Рк^,/™ ^ Ғтк/^,/т. НТС (д, U ) — это, во-первых, набор отображений д*8 : U*8 ^ Ғтк/^,/п. Таким образом, мы имеем набор векторных С^/п-расслоений £*8 := д*8(Рк/^,/п) ^ U*8 над попарными пересечениями U*8 .

Далее, в определение НТС входит также набор отображений д*8₇ : U*₈₇ х I ^ Ғт^ ,/2п, которому соответствует набор векторных С^/2п-расслоений £*8₇ : = д*8₇(Р_к/^,рп ) ^ U*8₇ х I таких, что

£*87 \u„p^ х{0} = £*8 0 £87\u«p7 и £*87 \u„p^ х{1} = £*7 0 7"" г» ■ , что следует из (15), (14), (12) и (13). В силу последнего свойства £*87 можно рассматривать как гомотопию над U*^ между рас слоениями £*8 0 £87 и £*7 0 [^Ь

Продолжая дальше, имеем набор отображений д*878 : U*878 х 1 ² ^ Ғтк/^ /зп и соответствующий набор векторных С^/3п-расслоений £*8₇8 ^:= д*8₇8 Фк/^/зп) ^ U*8₇8 х 1 ² таких, что

^£*878 |Ц_а/37|5х{ 0 }х/ = ^(£*8 ⁰ ^876 ^Уе Д^І х/;    ^£*878 ІУаД₇5 х/х{ 0 } = ^(£*87 ^{0 £}78 Ж’».-;-, і х/;

£*8781и„э^5 х{1}х/ = (£*78 0 ОФа^і х/;  £*878 \иар75 х/х{1} = (£*88 0 ОФа^ х/, и т.п. «Граничные» условия изображаются диаграммой

^£*8 ^{0 £}87 ^{0 0}8./- ^£*7 ^{0 £}78 ^{0 [}Н

^£аД ®^£Д^5 ^—                     — ^£а^5 ® [ ^/П ]

£*8 0 £88 0 Г ] , - £*8 0 [Z²ⁿ],

£«35 0^{[/ ]}

которая получается из диаграммы (16).

Тем самым мы пришли к следующему определению.

Определение 2. Гомотопическим снопом расслоений (£, У) называется набор C^/mn-векторных расслоений

£*0...*т ^ U*0...*m Х 1    , заданных для всех т > 1, которые согласованы в следующем смысле: если ст := («о ... «т), Сті := («о ... «»... «т) л (е, i)(Iт-1) — rj>aiib ti = е (е = 0 или 1). то для г = 1,..., т — 1

^£а |Ц_СТ х (1 ,і )( /т-1 ) = ^£ _СТі ^{0 [}П, ^£а |Ц_СТ х (0 ,і )( /т-1 ) = ^£*0...* ^{0 £}*і...*т .

4.    Стабильная теория4.1.    Стабильная тривиализация гомотопических коциклов

Следующий вопрос, на который нужно ответить, — какие HBG считать тривиальными? Для «обычного» снопа расслоений (Т(д), У ) условие тривиальности эквивалентно тому, что соответствующее главное РП(^)-расслоение происходит из П(^)-расслоения, см. (7). Естественным обобщением этого на случай рассматривамых нами HBG является условие редуцируемости структурного моноида до структурной группы, где имеется в виду вложение топологических моноидов

U(^/^) ^ Ғтк/^,/^

получающиеся как прямой предел отображений U(kl^m) ^ Frkim,in (ср. (9)). По техническим причинам нам удобно разложить эту редукцию на два шага: во-первых, сначала до проективной унитарной группы PU(kl ^ro ), а уже затем до унитарной группы U(kl ^ro ).

Определение 3. Пространство Grkimjn, параметризующее унитальные *-подалгебры, изоморфные Мыт (C), в фиксированной матричной алгебре Mkim+n (C), называется матричным грассманианом.

Простым следствием теоремы Нетер—Сколема является его представление

Gr_klm,_t„ — PU(kl^m+n)/(PU(kl^m) 0 PU(lⁿ))

как однородного пространства группы PU(kl^{m + n} ) всех *-автоморфизмов алгебры M_kim+n (C).

Через Gr_ki^,i^ обозначим прямой предел Нщ    Gr_kiт ^п матричных гр ас с маннанов

^m, п

Grympn относительно отображений, индуцированных унитальными *-гомоморфизмами матричных алгебр.

Имеется действие моноида Frki^,i^ на матричном грассманиане Grki^,i^, определенное на конечномерных подпространствах отображениями

• У ^{: Fr}ki^m+ⁿ,iP ^{х Gr}ki^m,iⁿ ^ ^Gr ki^m,iⁿ+p, y ^{( h}, Aki^m ) — h ⁽ Aki^m ) c ^Mki^m+n+p (C)

для гомоморфизма h E Fi_klm+njp — Hom„/_g (Mkim+n (C), Mkim+n+p (C)) и подалгебры Akim c Mkim+n (C). В частности, имеем коммутативную диаграмму

Frkim+n+p,i9 х Frkim+n,iP х Grkim,in

Frkim+n+P,i9 х Grkim,in+P

Gr

ki^m,iⁿ⁺p⁺q .

Y

Frkim+n,ip+9 X Grkim,in

Далее используются соглашения и обозначения, введенные после Определения 1.

Определение 4. Проективной стабильной тривиализацией¹ НТС (д, U ) назовем сле-

ҺГг дующие данные: набор отображений ha: Ua ^ Grki^jn, гомотопни дарhp ~ ha, т.е. отображения hap : Uap х I ^ Grki^,i2n такие, что hap lUap х{0} — даР hp, hap lUap х{1} — Ln, п ° ha, где бп п обозначает вложение Grki^gn ^ Grki^ pin, а дарhp — композицию diag            д™р хҺр                        ^

^Uap ^ ^Uap ^{х U}p --> r^rki”,i^{n х Gr}ki”,iⁿ ^ ^Grki”,i^2n;

далее гомотопии hap7, отвечающие квадратам да@ дР7 h7

даЗуҺу

^ ^даР ⁽ ^п,п ° ^hp ) ^{— 1} 2 п,п ° ^{( д}аР^hp ) ¹‘2п,п ^{о Һ}«б

° ha — 1П, _2п ° ha,

(Ьп,п ° да7)h7 — ^2п,п ° (да7h7) ^   ^^ ^2п,п ° ^п,п то есть ha^7 : Uap7 х 12 ^ Grki”, i3n,

Мы используем здесь термин «стабильный», чтобы избежать смешения с понятием тривиального Frfei“,і“-коцикла, см. [10]. Условие стабильной тривиальности существенно слабее условия тривиальности: ниже мы покажем, что оно эквивалентно тому, что гомотопический Fr^j^,;~-коцикл эквивалентен проективному коциклу, который не обязательно тривиален.

такие, что

^Һа3у ^„^ хі х{0} = 9аР^^Һу ,   ^Һа37 ^„^хі х{1} = ^L 2 n,n ° ^Һ«3 ,

^Һа37 ^„^ х{ 0 }хі ⁹«3^Һ3у , Һ_ару ^„^ х{1}хі   On, n ° ^Һ«7,

И Т.П.

В общем случае для всех m > 0 имеем отображения

Һ«0...«т : и«0...ат X I ^ Gr^/м,/(m+l)n такие, что для г = 1,..., m

НТС, для которого существует проективная стабильная тривиализация, называется проек-тивно стабильно тривиальным.

Расширение структурной группы PU(kl^m) до структурного моноида Ғгкі^,і^ описывается в терминах классифицирующих пространств следующим образом. Пусть

А^ ^ BPU(kl^m)

• —    универсальное М^іт (С)-расслоение. Применяя к нему послойно Hom_ai₉(..., Мкіт+п (C)) как функцию от первого аргумента, получаем некоторое Ғгкіт,іп-расслоение

Нкіт,іп(А^ ) ^ BPU(kl^m).                           (18)

Нетрудно показать, что имеет место гомотопическая эквивалентность

Нк1т,п (А^ ) - Gr кіт^іп , причем такая, что диаграмма

^Ғгкі^т+п,іР ^{X Н}кі^т, і^{п ( А}к;1т^и )

Нкіт,

univ\ і^{п+р ( А}кіт )

~

~

Gr

кіт,іп+Р

коммутативна. При переходе к пределу при т, п ^ то из (18) получается главное Рткі^,і^-расслоение над BPU(fcl^), действие моноида на тотальном пространстве которого отождествляется при гомотопической эквивалентности с его действием на Grкі^,і^- Оно классифицируется некоторым отображением

BPU(kl^) ^ ВҒг_кі^,_і^,                              (19)

получающемся при распетливании гомоморфизма моноидов PU(kl^ro) ^ Ғгкі^р^, аналогичного (17). Очевидно, (19) является расслоением с гомотопическим слоем Grкг^,l^ , которое имеет также следующую интерпретацию.

Предложение 4. Пусть

ЕҒгкі^,і” ^ ВҒгкі^,і”

• —    универсальное главное Ғгкі^,і^-расслоение. Тогда имеет место гомотопическая эквивалентность

ЕҒгкі^,і^   X Grкl^,l^ - BPU(kl“).

Ғгым, гм

Более того, расслоение

; ^,і^

^EFr кі^,і^   ^{X    Gr} кі^,і^

^Fr kl^ ,l^

^BFr кі ^, і^

эквивалентно расслоению

Gr_kl^,_l^ ^ BPU(kl^) ^ BFr_kl^,_l^.                        (21)

Замечание 2. Нетрудно показатв, что расслоение (21) эквивалентно расслоению

BPU(l“) ^ BPU(kl^) ^ BFrkl^,l^.

Доказательство. Заметим, что пространство ЕҒг^і^,і^   х    Gr .i”, i” совпадает с

Fn-m, т гомотопическим фактором пространства Gr.i^,i^ по действию моноида Fr.i”,i”. Поэтому, согласно сказанному в абзаце перед доказываемым Предложением, существует гомотопическая эквивалентность

^EFrki^, i”   ^{х   Gr}ki^,i^ ^{— H}ki-,i- (А.?™)^/Fr kl^,l^ ,

Frfci^, i^

а последнее пространство, как мы видели, есть BPU(kl^). Второе утверждение теперь очевидно. □

Следствие 1. НТС со значениями в Fr.i^,i^ проективно стабильно тривиален тогда и только тогда, когда он эквивалентен некоторому проективному коциклу (со значениями в группе PU(kl^m) для некоторого т Е N-

Доказательство. Заметим, что из Определения 4 следует, что стабильная проективная тривиализация НТС — то же, что отображение из кубической геометрической реализации симплициального множества, связанного с открытым покрытием Ы пространства X (и гомотопически эквивалентной X), в тотальное пространство расслоения (20). Оно отвечает подъему классифицирующего отображения X ^ BFr.i^,^, определенного (с точностью до гомотопии) исходным НТС (см. [10]). □

Для того чтобы вместо проективной определить унитарную тривиализацию, нужно заменить Hkim,i"(A^i™^y) пространствами Hkim,i"(End(^^^)), где £_k/™“ ^ BU(kl^m) — универсальное векторное C^kim-paccnoeHие. Пусть H.i^,i”(End(£k/S“)) ^— их прямой предел при т, п ^ то. Замет им, что H.i^,i” (End(£k¹/S“)) ^ BU(kl^) — главное Ег^^д^-расслоение, в частности, на его тотальном пространстве свободно действует моноид Fr.i”, i^. Если обозначить

Grki™,т := Hki^,in(End^T1)), Grki-,i- := Hi”, i”(End^T)), то будут иметь место аналоги предыдущих результатов (в частности, Предложения 4) с заменой Gr.i”,i” нa Gr .i”,i” и проективных унитарных групп на соответствующие унитарные. Теперь, используя действие моноида Frki”,i” нa Gr.i^,i^ (как на главном Frki”,i”-расслоении), получаем определение стабильно тривиального НТС (д, Ы) (ср. Определение 4).

Посмотрим, что произойдет в унитарном случае, если положить l = 1. В этом случае расслоение (ср. (20))

Hk, Ел;.-   )) ^ EFrk, 1 X Hk, ге.   )) ^ BFrk, 1

Е, 1

гомотопически эквивалентно расслоению (7). Так как Fr., 1 = PU(k) — группа, то НТС со значениями в Fr., 1 эквивалентен строгому коциклу, и мы возвращаемся к теории классических снопов расслоений, отвечающих проективным коциклам. В частности, такой коцикл стабильно тривиален тогда и только тогда, когда он эквивалентен некоторому унитарному коциклу.

4.2.    Стабильная тривиализация гомотопических снопов расслоений

Посмотрим, как стабильная тривиализация НТС может быть описана в терминах соответствующих HBG. Во-первых, заметим, что над матричным грассманианом Grk/m,/n определено тавтологическое М^т (С)-расслоение (над точкой ж G Gr^/ т /п «ВИСИТ» ПОД ЯЛ^-гебра в М_к/т+п (C), параметризуемая этой точкой). Это расслоение является подрасслоением тривиального расслоения Gr^/m,/n х Мут +> (C) (причем каждый слой является унитальной подалгеброй). Беря его послойный централизатор, получаем некоторое М/п(C)-расслоение над Gr^/m,/n. В унитарном случае определяется аналогичное векторное С^/п-расслоение Чк/т,/п ^ Gr^/m,/n. Для отображений

̂︁̂︁

У • Frk/m+n,/P х Grk/m,/n ^ Grк/т,/п+Р, определяющих действие моноида Frk/^,/^ нa Grk/^,/^, имеем

V ^{( ч}к/^т,/^п+Р ) = 'к/^т+п,/Р ^ ^рк/^т,/^п .

Определение 5. Стабильная тривиализация для HBG Д, У) состоит из следующего набора данных. Во-первых, это набор векторных С/п-расслоений ра ^ Ua; затем набор векторных C п-расслоений чаР ^ Uар х I таких, что раР\иар х{0} = ^аР 0 рР, раР\иар х{1} = Ча 0 [^ ];

затем набор векторных С^/3п-расслоений ЧаМ ^ U_ap^ х 1 ² таких, что

^ЧаР^ \u_a^₇ хІ х{ 0 } = ^аР^ ^{0 р}7,    ^раР^ \и_а^₇хІх{ 1 } = ^раЦ ^{0 [}^ ^];

ЧаР^\ua^7х{0}хІ ^аР 0 ЧР^(,   раР^\иа^7х{1}хІ ра^ 0 [^ ], и т.д. На т + 1-м шаге имеем иабор векторных С/(т+1)п-расслоеішй

таких, что для г = 1,..., т

^Чао...ат 1и_а0..._ат х (0 ,г )( І^т ) = €ао-«і ^{0 р}а^...ат ^{; Ч}ад...ат Іи_а0..._ат х (1 ,г )( І^т ) = ^Ча₀„.а_і...ат ^.

Заметим, что при I = 1 (и замене гомотопического коцикла строгим) мы возвращаемся к обычной тривиализации соответствующего снопа расслоений (L, У ): напомним [2], что это — набор линейных расслоений Ч_а ^ U_a и изоморфизмов Е_аР 0 ч р ^= Ч_а ^наД и_аР .

4.3.    Стабильная эквивалентность

Понятия стабильной тривиальности гомотопических коциклов и снопов позволяют определить соответствующую стабильную эквивалентность. Для этого заметим, что помимо операции, отвечающей композиции гомоморфизмов (которая приводит к операции в моноиде), на пространствах Frk^ /т,/п есть еще операция

Frkr/т,/п х Frks/P,/9 ^ Frkr+S/m+p,/n + q , индуцированная тензорным произведением матричных алгебр. После перехода к прямому пределу она определяет гомоморфизм моноидов

Frkr/”,/” х Frks/^,/^ ^ Frk^+s/”,/” .

Возникает соответствующая операция тензорного произведения на гомотопических коциклах и гомотопических снопах. Два НТС назовем стабильно эквивалентными, если они становятся эквивалентными после тензорного умножения на стабильно тривиальные НТС; аналогично для HBG. В результате мы получаем группу классов стабильной эквивалентности НТС (и HBG) относительно операции, индуцированной тензорным произведением.

Данное отношение эквивалентности аналогично отношению эквивалентности на проективных коциклах, возникающему из операции «тензорного произведения» проективных групп

PU(kr) х PU(ks) ^ PU(kr+s), классы эквивалентности которого соответствуют подгруппе k-кручения

Brk(X) = coker{[X, BU(k^)] ^ [X, BPU(k^)]} = im{[X, BPU(k^)] ^ [X, K(Z, 3)]} в топологической группе Брауэра Br(X) = H3,rs(X, Z).

Следующая теорема обобщает сформулированный результат.

Теорема. Группа классов стабильной эквивалентности HBG, получающихся из гомотопических Ет^г 1^,1^-коуиклав (г Е N, естественно изоморфна группе coker{[X, BU(k^Z^)] ^ [X, BErfc<^,^]}

(ср. (21)), а таксисе образу «отображения Диксмъе—Дуади» Дм. Замечание 2):

im{[X, BEr_k^,^ ] ^ [X, BBU(Z^)]}.

Доказательство. Согласно [10], классы (обычной) эквивалентности НТС со значениями в моноиде Ет^г/^,/^ находятся в естественном взаимно однозначном соответствии с гомотопическими классами отображений X ^ BEr^r/^д^. Используя «унитарный» аналог Следствия 1, нетрудно показать, что два НТС стабильно эквивалентны тогда и только тогда, когда их классифицирующие отображения X ^ BEr^r/^д^ отличаются на некоторое отображение X ^ BU(k^rI^ю). □

Таким образом, HBG с введенным отношением стабильной эквивалентности дают геометрическое представление элементов [X, BBU(Z“)], принадлежащих (после локализации по Z) второму множителю в (1). отвечающему «высшим» скручиваниям в ^-теории.

Из результатов статьи идея рассматривать коциклы со значениями в моноиде принадлежит первому автору, которому также принадлежат результаты главы 2, § 3.1 и Определение 2. Важные Определения 4 и 5 предложены вторым автором, а их интерпретация в терминах действия моноида — первым, которому также принадлежат Предложение 4 и теорема из § 4.3.

Работа первого автора была поддержана грантом РФФИ №11-01-00057-а.