Гомотопия решений уравнения минимальных поверхностей

Уравнение минимальных поверхностей известно уже более 200 лет, но его точных решений до сих пор построено всего три. Это такие поверхности, как катеноид, поверхность Шерка и семейство геликоидальных поверхностей.

Рассмотрим поверхность вида

Поскольку (7) удовлетворяет линейному уравнению (4), то их гомотопия также является решением уравнения (4). Тогда wH = a (n arctg i) + (1 - a )x

z=u ( x , y ).

V i + i²

x - i arctg i + n arctg n + ln У

Это уравнение описывает минимальную поверхность, если u ( x , y ) удовлетворяет уравнению второго порядка

( 1 + u_x ² ) u - 2 u^u + ( 1 + u„ ² ) u = 0.       (2)

xyyxyxyyxx

С помощью контактного преобразования Лежандра

w _H ² = a (n arctg i) + + ( 1 - a ) x

ux = i, uy = n w = x, w = y, u (x, y) = x i + yn - w (i, n)(3)

уравнение (2) сводится к линейному:

(1 + ^2 )wii + 2^Пwin +(1 + П2 )wnn = 0, при условии, что якобиан преобразования

J = "" - Uxv * 0.(5)

xxyyxy

Нетрудно проверить, что поверхности cosx u = x tg y, u = In-----, U = arcch (x + y ), cos y т. е . геликоид, поверхность Шерка и катеноид соответственно, являются решениями уравнения (2) и удовлетворяют условию (5).

Применим преобразование (3) к соотношениям (6),

x

- In x

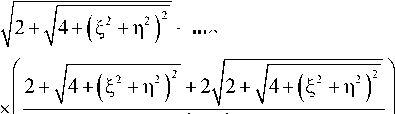
, i2 + n2

w н = a

J1 + i² ^

- i arctg i + n arctg n + ln ,

+ ( 1 - a ) x

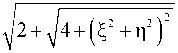
2 + J 4 + ( i² + n² ) ² + 2^2 + ^4 + ( i² + n² ) ² i^^n²

тогда они запишутся в виде w (i, n) = n arctg i, w(i, n) = -i arctg i +

Vi+12"

+ n arctg n + ln ,      ,

Vi+n2

где w ¹ _н , w_н ² , w_н ³ – новые решения уравнения (4); a – вещественный параметр, 0 <  a <  1.

Действуя обратным преобразованием, из (8) получим новые семейства решений уравнения (2).

- ln

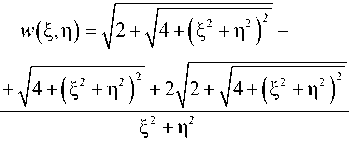
A

.

S. I. Senashov, O. N. Cherepanova

HOMOTOPY OF MINIMAL SURFACES EQUATION SOLUTIONS

The new exact solutions of minimal surfaces equations are constructed in this work.