Горизонтальные перемещения 2-х слойного основания с подстилающими слабыми водонасыщенными слоями под колоной круглого сечения при динамических нагрузках

Введение:  Во многих подземных сооружениях несущими конструкциями являются колоны круглого сечения, для которых используют квадратный либо прямоугольный фундамент стаканного типа. Под фундаментами должны залегать прочные грунтовые основания либо уплотненные песчанные подушки. Но эти уплотненные слои или песчанные подушки обладают меньшей толщиной относильно к высоте активной зжимаемой зоны, которая воспринимает колебания от вибраций или импульсов динамических нагрузок. Высота активной зоны основания может достигать до 12м и более.

В некотрых литературных источниках встречается расчёт оснований сооружений при динамических нагрузках. Однако поведение оснований гризонтальных смещений при вынужденных колебаниях через колоны недостаточно изучено, хотя это часто встречается в инженерной практике, что характерезует актуальнсть проблемы.

Цель работы. Дать оценку устойчивости 2-х слойного основания со слабыми подстилающими слоями при динамических нагрузках под колоной круглого сечения, в случаях когда вибрационные или импульсные нагрузки передаются на слабый подстилающий слой.

Изложение результатов исследований.

Колона круглого сечения, как несущая конструкция подземных сооружений от статических нагрузок собственного веса сооружений с технологическим оборудованием, машинами и механизмами, а также от динамических нагрузок этих машин и механизмов, передает нагрузку на 2х слойное грунтовое основание. При этом, в основном, 1-й слой обладает хорошими прочностными свойствами, но имеют малую толщину

(примерная толщина 1-го слоя до 0,6м), 2-й слой состоит из слабого подстилающего слоя большой толщины (примерно до 12м). В таких случаях, 2-му подстилающему слабому слою приходится воспринимать всю действующую нагрузку, особенно вибрационную или импульсную динамическую нагрузку от технологических машин и механизмов. Под действием этих нагрузок слабый подстилающий слой имеет вертикальную и горизонтальную составляющие перемещения.

В данной статье будем рассматривать колебания 2-х слойного основания в горизонтальном направлении. Перемещения в горизонтальном направлении возникают от передаточных функций динамических нагрузок через колоны круглого сечения и фундаментов стаканного типа.

Для облегчения расчёта колебаний системы “колона - фундамент - 2х слойное основание” условно принимаем колону и фундамент стаканного типа абсолютно жесткими “штампом”, 1-й слой наиболее прочных грунтов имеет малую толщину. Тогда 1-й слой основания совместно с фундаментом и колоной круглого сечения составляют систему, которая передает динамическую нагрузку в гармоническом режиме колебаний, полупространству слабого подстилающего слоя основания (рис. 1).

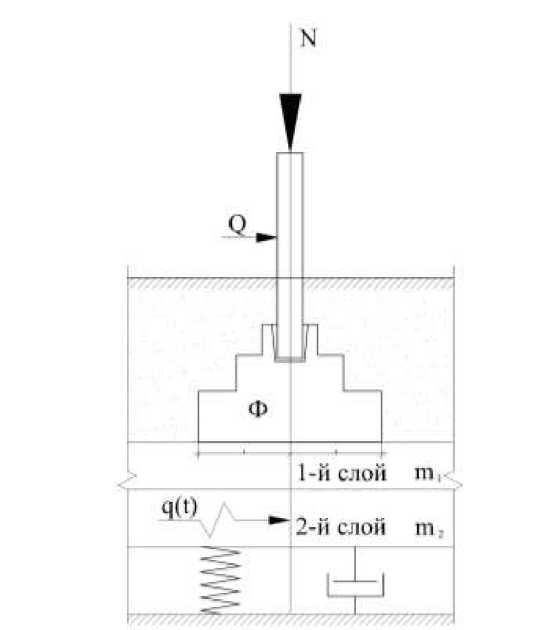
Рис. 1 Расчётная схема колебаний системы “колона - фундамент - 1-й слой - 2-й слой”.

Распределенную динамическую нагрузку в виде установившегося гармонического колебания системы принимаем в следующем виде:

q ( t ) = Q ;

Которые создают горизонтальные колебания системы в следующем виде:

S-c.         S-e.

;

U ( t ) = —^- U _oo = —^- ( U₀₁ +U₀₂ +U ₀₃) 2;r VG ⁰⁰ 2^?G^{V 01   02   03} (2)

При этом систма имеет одну степень свободы, где динамические вибрационные или импульсные нагрузки передаются через колону, фундамент, 1-й слой на 2-й, слабый, подстилающий слой. Нагрузка q(t) с массой фундамента Ф и массой m 1 1-го слоя создает во 2-м слое уплотненную зону массой m 2 с передаточной функцией U(τ).

Здесь U(τ) - горизонтальные перемещения от динамических нагрузок гармонического режима колебаний, которые возникают от передаточных функйций U 00 . Передаточные функции в горизонтальном направлении U 00 имеют три составляющих передаточных функций.

U 00 =U 01 +U 02 +U 03                          (3)

Q - интенсивность динамических и статических нагрузок;

ω - угловая частота вынужденных колебаний;

i - мнимая единица; S - величина вибрации или импульса (можем принимать из паспорта машин и механизмов);

c = JX+IgT^ - скорость поперечных волн, здесь, не учитывается в горизонтальных перемещениях,

C1 = -^G / p0 - скорость продольных волн, tE c , t - время;                - постоянная Ляме;

r’     p ’    (1 + А0(1-2р)                         ’

μ - коэффициент Пуассона фундамента для железобетона μ=0,25÷0,5;

G=0,7E - модуль сдвига для железобетона или параметр Ляме;

r - радиус или половина ширины круглого либо прямоугольного (квадратного) фундамента;

E - модуль упругости материала фундамента;

ρ 0 =γ - плотность или удельный вес фундамента;

η=с2/с1 - коэффициент зависимости от соотношений продольных c211-2p волн к поперечным: 2) = — = л;

С1

принимаем для реологических параметров 1-го слоя упругую пружину Гука. K 1 =2πrρ 0 c 1 и демпфер Ньютона b 1 =πr²ρ 0 c 1 .

Для 2-го слоя

_  3    ^   _  3 ,Х Л2       1    2^2 _ _

m       r         r K     rG br c

2 H      pH H °  ’  2 H '    HI’

Величины: β=1,6 при μ=0; β=1,79 при μ=0,25; β=2,12 при μ=0,25; Д=4,29 при μ=0; Д=4,22 при μ=0,25; Д=5,54 при μ=0,3; H=1,68 при μ=0; H=1,32 при μ=0,25; H=1,23 при μ=0,5.

Составляющие компоненты горизонтальных передаточных функций определяется следующей формулой:

Где

U 01

U 02

^U 03 -

1 71Д ( y ) R ( y , т) при т <  2 y ;

[ 0 при т >  2 у ;

( Д1.r(У1)R (У1т) dy пРит <1гР т/2

0 при т > Ър

1                                       1              “2

/Д 2. r ⁽ У 1 ) ^{R (} У1^т)dy 1 + j⁽¹- У 1 ) ^{R (} У\^т)dy пр^{и т} <2/;

п

т /2

j   Д 2. r ⁽ У 1 ^{) + (}1- У 1 ) ^{2 R (} yj)dy 1 пР^{и 2}

т /21_                                 _

0 при 2 < г;

Д 0⁽ У 1^{) =} «R ⁴ y 1 — +

I У 1

Л ^а R  РR _ 2

RR

-1

Д 1. r ⁽ у 2 ⁾⁼« 1[ ⁽² У 1²- ¹⁾⁺⁴ У 1²А^1]¹

2   1\2          2   2

2. r ^{( y} 1 ^{) — (2 y} 1 ^— 1) ^1 ^{(2 y} 1 ^—1) +¹⁶^ 1 А

r ^— V y i   1; Pr ^— V y 1     ; ^1 ^_V^{1   y} 2 ; Р\ ^— V^    ^y 2 ; ^2 ^_V y 2   1; А ^_V y ^    ~п"•

Функция по формуле (2) может быть аппроксимирована выражением:

Здесь y 1 и y 2 смещение грунтов оснований в горизонтальном направлении по оси Y.

График передаточных функций динамических нагрузок в горизонтальном направлении U 0 (τ) для коэффициента μ=0,25 представлен на рис. 2.

График аппроксимирующий функции (9) показан на рис. 2 пунктиром. Функция (9) определяет горизонтальные перемещения системы в виде пружины и демпфера, соединенных паралельно (рис. 3), под действием мнгновенного импульса в отрезке времени.

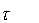
U (r) = —2^ e ^” тс r¹G

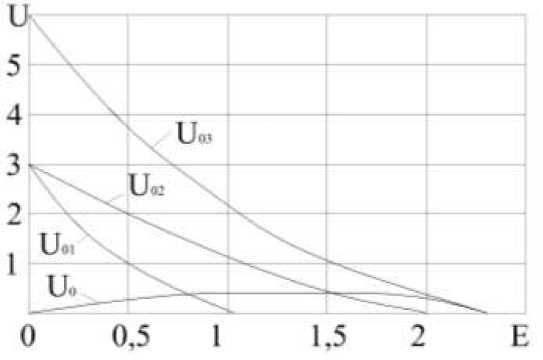
Рис. 2. График функции U 0 (τ) для коэффициента Пуассона μ=0,25.

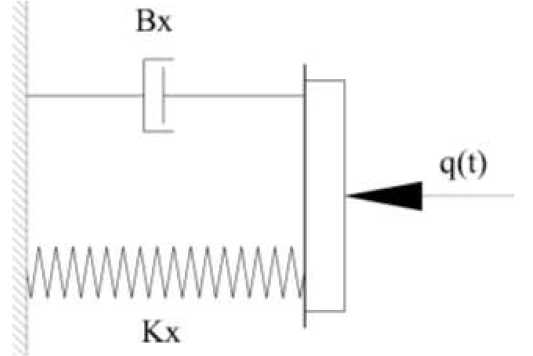
Рис. 3. Реологическая модель смещения несущих конструкций под действием импульсно-динамической нагрузки.

Это дает возможность задачи о нестационарных горизонтальных колебаниях условно принятого штампа на полупространстве заменять с полупространством нашей системой с реологическими параметрами, которые равны:

K x

8 rG

Bx^^r ^Pc c 2 ;

Записываем передаточные функции в следующем виде:

U 1 =

P

2л-² Gr

( f ,+ f _t ) ;

Графики f 3 f 4 при различных значениях ω 0 , μ=0 и μ=0,5 представлен на рис. 4.

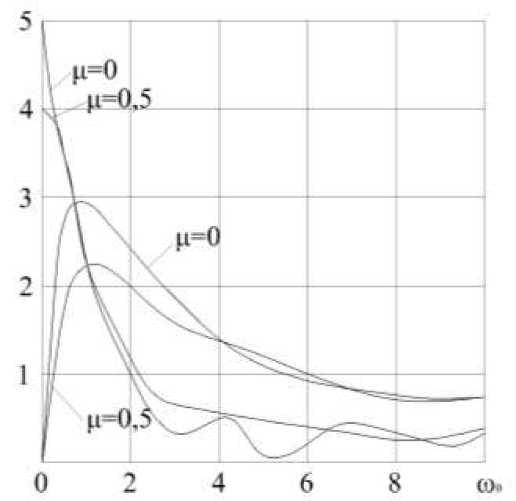
Рис. 4. Графики f 3 и f 4 при различных значениях ω 0 , μ=0 и μ=0,5.

Реологические параметры II-го подстилающего слабого слоя основания пружина Kx(ω) и демпфирование зависит от частоты ω и в гармоническом режиме колебаний для штампа (фундамента динамической нагрузки следующими формулами:

K И = 2ж² Grk x («и K (»„) = — f -^ ;

- f 4

® o( f _s²+ f 2 )

B x Gy^{) = 2}r² r²Pc^c 2 b x (to o ); b_x (®₀) =

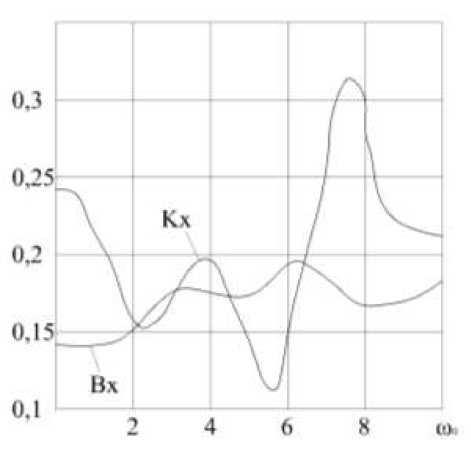
Рис. 5 Графики K x (ω 0 ) и B x (ω 0 ) при μ=0,25.

Ф+Т 1 ) и

Для практических расчётов величины K x (ω 0 ) и B x (ω 0 ) можно определять следующим выражением:

KxW = 0,236-0,013^2; BxИ) 0,141 (13)

Графики K x (ω 0 ) и B x (ω 0 ) при μ=0,25 показаны на рис. 5.

Выводы: Динамические нагрузки на двухслойное основание, нижний слой которого, состоит из слабых водонасыщенных грунтов, вызывают очень сложные колебания и перемещения грунтовой массы, что, в свою очередь, негативно сказываеся на подземном сооружение в целом. По этому необходимо детально изучить, с помощью эксперементов, влияние динамических вооздействий на основание подземных сооружений, с целью выявления наиболее рациональных решений проблем устойчевости оснований со слабых, перенасыщенных водой, пород под воздействием динамических нагрузок.

колебания, горизонтальные перемещения, слабый подстилающий слой, передаточные функции, угловая частота, упругие пружины, вязкий демпфер, амортизатор, вибрация, импульс, активная зона, реология vibration, horizontal displacement, weak underlying layer, transfer functions, the angular frequency, the elastic spring, viscous damper, shock, vibration, pulse, active zone, rheology