GPU Optimized Stereo Image Matching Technique for Computer Vision Applications

Published Online May 2015 in MECS

Feature selection and matching is a key component in many computer vision tasks such as path finding, obstacle detection, navigation, stereo vision, and many others applications [1-6]. Several strategies of keypoint detectors have been proposed in the literature [7-8]. Schmid and Mohr [9] used Harris corners as interest points in image recognition problems to match the features against a large database of images. This method allows features to be matched under arbitrary orientation changes, but it is sensitive to image scale changes. Lowe [10] proposed the scale invariant feature transform (SIFT) descriptor for the extraction of interest points in an image that is invariant to both scale and rotation. The SIFT technique used a 128-dimensional vector to describe the SIFT feature, which is computationally intensive. In a recent research [11], we have implemented an efficient feature matching technique faster than Lowe’s SIFT with self-organizing map (SOM) that can be used for real-time stereo matching applications. In the present research, we extended our research and implement our proposed method on graphics processing unit (GPU) to further optimize the time.

Due to the advancements of parallel processing techniques, multi-core GPU techniques have been widely applied to accelerate the computationally intensive tasks [12]. Modern programmable graphics hardware contains powerful coprocessors GPUs with a peak performance of hundreds of Giga FLOPS which is an order of magnitude higher than that of CPUs [13]. For accelerating the applications of computer vision many researchers are now exploiting parallelism provided by modern programmable graphics hardware that provides a great scope for acceleration to run computations in parallel [1415]. Some researchers also utilized specialized hardware and reconfigurable hardware to speed up these algorithms [16-18]. One example of a broad area of application is in discovering concurrency in parallel computing, where coloring is used to identify subtasks that can be carried out or data elements that can be updated simultaneously [19]. Another example of a broad application area of coloring is the efficient computation of sparse derivative matrices [20]. With the increasing programmability and computational power of the GPU, the recent work by Sinha et al. [12] accelerates some parts of the SIFT algorithm using the hardware capacities of GPUs. A 10x speedup is obtained, allowing for applications on videosized images [12]. A variety of computer vision algorithms has been parallelized, providing significant acceleration to the computation [12, 14, 15].

In this paper, a novel technique is presented that is designed to achieve fast feature matching in the images with the use of neural networks and GPUs. Our contribution is the proposal of a GPU-optimized matching technique based on Kohonen’s self-organizing map (SOM) [21]. The proposed method provides significant reduction in the computation time compared to Lowe’s SIFT. In our approach, the scale space for keypoints extraction is configured in parallel for detecting the candidate points among which the number of keypoints is reduced with the SOM neural network. The descriptor vector generation is accelerated on the GPU and the matching is accomplished with competitive learning. The key idea is to optimize the keypoint extraction with GPU and to reduce the descriptor size with the winning calculation method. The similar winning pixels in the images are found and associated to accomplish the feature matching. The proposed method of the GPU is faster due to the usage of multi-processing.

The remainder of this paper is organized as follows: Section II describes the overview on stereo vision. The procedure of feature matching with GPU-optimized method is presented in section III. The experimental results are shown in section IV and conclusions are drawn in section V.

• II.    Stereo Vision

Stereo vision is based on acquiring three-dimensional (3D) information from different views obtained by a single moving camera or a fixed structure composed of at least two cameras. The goal of stereo vision is to obtain a 3D structure of a scene with the use of two or more images of a 3D scene, each acquired from a difference viewpoint in space. The 3D location of any object is limited to the straight line that passes through the center of project and the projection of the object point. The position of a point in space is determined by obtaining the intersection point of the two lines that passes through the center of projection and the projection of a point in each space. The triangulation principle is based on computing the 3D position of an object point from the intersection of a set of optical rays determined by at least two views of the same 3D object point. The optical axes of the two camera-lens units are configured in parallel, and the straight line joining the two optical centers is parallel to each image horizontal line in order to respect an epiploar constraint (Fig. 1). The 3D image information is obtained on the basis of position of the points in the left and the right images [22].

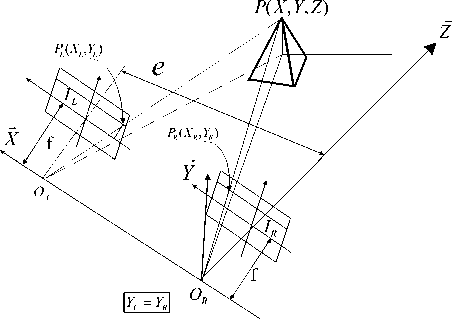
Fig. 1. Stereo vision system configuration to obtain 3D object point.

The coordinates of a 3D point P of an object is given by coordinates ( X P , Y P , Z P )

_ x x e       y _x e        f x e

XP         s YP "" ------ё ZP         s

Px x 8     Px X 8      Px x 5

,, where e denotes the distance between the two optical centers, px denotes the CCD pixel width, f denotes the focal length of the two lens, and 8 denotes the disparity of P.

The disparity is defined as the difference in the location of an object point between the left image and right image. ( X L , Y L ) and ( X R , Y R ) are the coordinates of the projection of point P in the two images, left and right image respectively (Fig. 1). The disparity is given by 8 = X_L — X_R i.e. the difference in the position in the left and right image.

The approaches to find stereo correspondences are divided into two categories: one based on sparse local features that are obtained between two matched images, and the other based on matched regions after pixel by pixel matching in the different images. These technique can be used to obtain the 3D object recognition and categorization, in addition can be used for 3D scene reconstruction. The depth at various scene points can be obtained by determining the disparities of corresponding image points. Due to the discrete nature of the images, the disparity is obtained in terms of integer values unless some special algorithm is designed to compute the disparity values. The accuracy of depth computation for any given set of camera parameters can be enhanced by increasing the length of the baseline and large disparity can be obtained for any 3D scene.

• III.    Proposed GPU-Optimized Matching Technique

In this section, we explain our proposed GPU-based method to optimize the features in image matching along with the SOM methodology. The GPU is a specialpurpose processing unit that has been used as a generalpurpose processing unit due to its single instruction multiple data (SIMD) parallel hardware structure. With the advent of multi-core CPUs and many-core GPUs, the mainstream processor chips are now parallel systems. Also their parallelization continues to scale with Moore’s law. Compute unified device architecture (CUDA) considered GPU hardware as an independent platform that can provide a programming environment and minimize the need for understanding the graphics pipeline. The GPU hardware chip has N × multiprocessors (MP), and each MP has M × scalar processors (SP) (Fig. 2). The memory of the GPU is organized into global, shared and constant. In addition, there are registers, which are the local memory of threads [23]. When the kernel function to be executed with CUDA is ready, a grid composed of one block must be configured. The block generates a large number of threads to share data with other threads and then parallel processing can be performed. The thread is composed of hierarchical SIMD architecture and the mass of a thread is called the thread block that is used to assign CPU job to GPU. A GPU executes multiple threads in parallel and independently processes streams of vectors in parallel. For computing, the load/store instructions access three read/write memory spaces: local memory for per-thread, private, temporary data; N shared memory for low-latency access to data shared by cooperating threads in the same streaming multiprocessor (SM); and N global memory for data shared by all threads of a computing application.

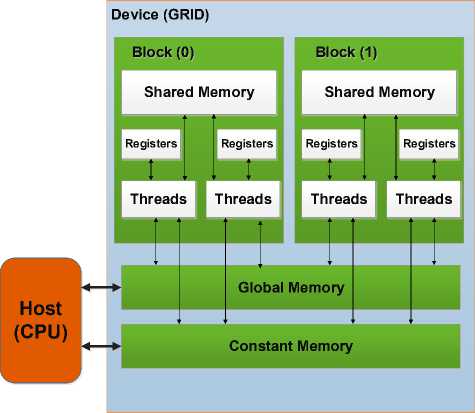
a) Memory, thread and block Organization

SM, vertex, geometry, and pixel threads have independent input and output buffers. Workloads can arrive and depart independently of thread execution. The SM maps the warp threads to the SP cores, and each thread executes independently with its own instruction address and register state. A SIMT processor realizes full efficiency and performance when all 32 threads of a warp take the same execution path.

A. Parallel Scale Space Configuration And Construction Of Descriptor

In our approach, the construction of Gaussian scale space is accelerated on the GPU using fragment programs. In order to extract the candidate keypoint, the scale space L ( x , y , 7 ) is computed in parallel by the convolution of a variable-scale Gaussian G ( x , y , 7 ) over the input image I ( x , y ) .

L ( x , y , ст ) = G ( x , y , ст ) * I ( x , y )

Device (GPU)

Processor-1:

Vertex

Host (CPU)

Output From the GPU

Graphics

Position and Coordinates input

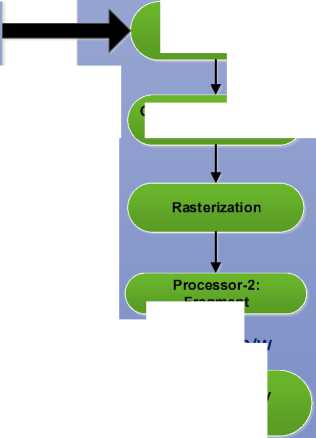
Geometric Operational unit

Fragment

R/W

Uploading

Texture

(b) GPU Graphics Framework.

Texture Memory (Video)

Fig. 2. GPU Architecture a) Memory, thread and block Organization, (b) GPU Graphics Framework.

where * is the convolution operation in x and y , and

G ( x , y , ст ) =

2Пст1

e - ( x ² + y ) 2 7 ²

Stable keypoint locations in scale space can be computed from the difference of gaussians (DOG) separated by a constant multiplicative factor k given by (3):

D ( x , y , CT ) = ( G ( x , y , к ст ) - G ( x , y , ст )) * I ( x , y )

= L ( x , y , к ст ) - L ( x , y , ст )

Downloading Texture

The intensity image, gradients and the DOG values are stored in a GPU texture format and computed in parallel in the same pass using vector operations in fragment programs. The Hessian matrix H ( x , y , CT ) is computed by the second-order derivative of the Gaussian blurred image by (4):

The GPU host interface unit communicates with the host CPU, responds to commands from the CPU, fetches data from system memory, checks command consistency, and performs context switching. The load distribution units pass the input assembler’s output stream to the array of processors in order to execute vertex, geometry, and pixel shader programs, as well as computing programs. The streaming processor executes graphics shader thread programs and GPU computing programs to provide thread control and management. The SM is a unified graphics and computing multiprocessor that executes vertex, geometry, and pixel-fragment shader programs and parallel computing programs. The shared memory holds graphics input buffers or shared data for parallel computing. To pipeline graphics workloads through the

H ( x , y , 7 ) =

L xx ^{( x} , y^{, 7} )

^L xy ^{( x} , y^{, 7} )

^L xy ^{( x} , y^{, 7} )

L yy ^{( x} , y^{, 7} )

where L denotes the second-order derivative of the xy

Gaussian image in both horizontal and vertical directions. The equal number of threads has been assigned 7 ,...., 7 according to the number of given variables scaled for Gaussian operations to construct individual pyramids of m octaves simultaneously. Let mI be the number of features detected in I and D be the dimension of descriptors ( D = 128). A texture of size mI × D is created and filled with the mI descriptor values, each one occupying a column.

• B.    Winner-Based Image Matching And Acceleration Using Graphics Processing Unit

We used the SOM algorithm to map the highdimensional keypoints to a lower dimensional space with competitive learning [21]. The Self-Organizing Map was developed by professor Kohonen. The SOM algorithm is based on unsupervised, competitive learning. It provides a topology preserving mapping from the high dimensional space to map units. Map units, or neurons, usually form a two-dimensional lattice and thus the mapping is a mapping from high dimensional space onto a plane. The Self-Organizing Map (SOM) is a powerful neural network method for the analysis and visualization of high-dimensional data. SOMs are a data visualization technique which reduces the dimensions of data through the use of self-organizing neural networks. It maps nonlinear statistical relationships between highdimensional measurement data into simple geometric relationships, usually on a two-dimensional grid. The mapping roughly preserves the most important topological and metric relationships of the original data elements and, thus, clusters the data according to the input to the network. The need for visualization and clustering occurs, for instance, in the data analysis of complex processes or systems. Fig. 3 summarizes the complete algorithm of our approach.

To optimize the algorithms, the descriptor and locator section is implemented on the GPU to solve the complexity of feature matching that consumes a lot of time to obtain the descriptor vector. To implement this, the keypoints are scanned to obtain the descriptor and locator vector which are organized in a parallel fashion on the GPU. These vectors are processed separately and the scanning and organization is carried out in a parallel fashion on the GPU. These processors consist of a front end that reads/decodes and launches instructions and a backend made up of a group of eight calculating units and two super function units (SFUs) where the instructions are executed in SIMD fashion, the same instruction is applied to all the threads in the warp. NVIDIA calls this mode of execution for single instruction multiple threads (SIMT). The streaming multiprocessors’ operating mode is as follows:

• (a)    At each cycle, a warp ready for execution is selected by the front end, which launches execution of an instruction.

• (b)    To apply the instruction to all 32 threads in the warp, the backend will take four cycles, but since it operates at double the frequency of the front end, from its point of view only two cycles will be executed.

Our proposed approach used scale invariant feature vectors instead of an image database for the input to the SOM network. The topological map is obtained with the use of SOM network and we obtain a 2D neuron grid where each neuron is associated with a weight vector with 128 element descriptors. The 128 dimension descriptor generation is accelerated using GPU to increase the execution speed of the algorithm. The descriptor vector is read and its value is recorded individually in an array and also total value is recorded using the built-in libraries. The value is later used as a limit for declaring the threads and blocks for the GPU. As per the limit of each block only 512 threads can be accommodated in each block and there can be total 65536 blocks in a grid. Each value is dedicated to each thread in a block, the number of blocks depends on total values divided by 512 (number of threads). The inspection of the keypoints indicates that first four values are for locator and remaining 128 values are for descriptor so these threads will organize accordingly; the locators and the descriptors will be fetched in a parallel manner and organized accordingly.

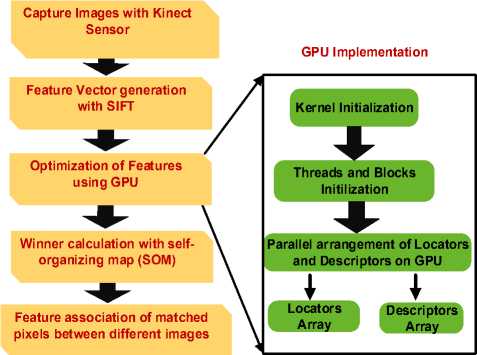
Fig. 3. Complete algorithm of our approach.

In order to perform the matching between the images, the learning algorithm is based on the concept of nearest neighbor learning. One image is considered as the reference image and the next image is considered as the matching image, and they are represented in terms of the winning neurons in the SOM network. After the network is trained, input data are distributed throughout the grid of neurons. The feature vectors are arranged according to their internal similarity with the SOM, thus forming a topological map of the input vectors. The winning neuron is found for each pixel of the next image and the pixel value is associated to it once the winner is found. The feature matching is performed by associating the similar winning pixels between the pixels of the reference and the next image. By iteratively repeating these process steps, the winning pixels are obtained with the selforganizing map and the matching between the pixels of the different image pairs is accomplished.

• IV.    Experiment And Analysis

In this section we give some experimental results to show the performance of the proposed method. We show experiments on images captured with the kinect camera designed by Microsoft, present results for 15 images and compared the performance of our method with Lowe’s feature matching method. The CPU algorithm is implemented on Intel (R) Core (TM) i3 CPU whereas its counter part of GPU is implemented on NVIDIA’s GeForce 310. The GPU-SIFT is implemented using CUDA. CUDA is a trademark of NVIDIA which is launched by the end of 2006. CUDA comes with a software environment that allows developers to use C as a high level programming language. The image size used for the analysis is 480 X 380. The experiments were conducted under diverse environment conditions such as rotation, scaling and blurring. Fig. 4 shows the matching results for the two images with Lowe’s method and with our proposed method. It is found that the average matching time is 0.13953 seconds for Lowe’s SIFT and the average time of proposed feature matching is 0.01447 seconds which is reduced to 0.00165 seconds using GPU optimization.

Using our proposed method, Lowe’s algorithm is speeded-up approximately 9x, further with the help of GPU, the proposed method is speeded-up more approximately 9x so a total of approximately 80x improvement in the execution speed is achieved. Table 1 shows the comparison results of the computation time for the two image sets with CPU and GPU. Fig. 5 shows a comparison of the results with GPU optimization, and the experimental results showed that the proposed algorithm performed more efficient matching than Lowe’s SIFT algorithm. Significant reduction in the computation time is obtained with the use of a GPU.

Lowe’s Proposed

a

b

c

d

Fig. 4. Matching results for the two images with Lowe’s method and with our proposed method.

Lowe's SIFT

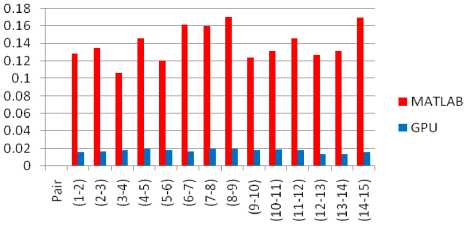
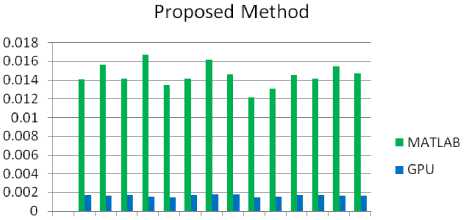
Fig. 5. Graphical comparison of computation time on different images with GPU optimization with Lowe’s method and the proposed method.

Table 1. Comparison of computation time on different images with CPU and GPU

S. No	Set of Images	Lowe’s Method		Proposed
		CPU	GPU	CPU	GPU
1	Image 1&2	0.1285	0.0156	0.0141	0.0017
2	Image 2&3	0.1345	0.0162	0.0156	0.0016
3	Image 3&4	0.1058	0.0177	0.0141	0.0017
4	Image 4&5	0.1456	0.0199	0.0167	0.0015
5	Image 5&6	0.1206	0.0182	0.0134	0.0014
6	Image 6&7	0.1612	0.0166	0.0141	0.0016
7	Image 7&8	0.1598	0.0199	0.0161	0.0018
8	Image 8&9	0.1701	0.0194	0.0145	0.0017
9	Image 9&10	0.1234	0.0182	0.0121	0.0014
10	Image 10&11	0.1314	0.0192	0.013	0.0015
11	Image 11&12	0.1456	0.0181	0.0145	0.0017
12	Image 12&13	0.1267	0.0133	0.0141	0.0017
13	Image 13&14	0.1312	0.0131	0.0154	0.0016
14	Image 14&15	0.1687	0.0155	0.0146	0.0016

• V.    Conclusion

This paper proposed a novel matching method to obtain the features under diverse conditions with reduced processing time. The computation time of the proposed method is reduced compared to Lowe’s method and optimized using a GPU. The experiments on various test images have been carried out to evaluate how well the proposed method performs on the matching problem compared to Lowe's method. Results in experiments show that the proposed method produces better matching results with significant reduction in computation times.

• [1]    M. Z. Brown, D. Burschka, and G. D. Hager, “Advances in computational stereo,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 25 issue. 8, pp. 993–1008, 2003.

• [2]    T. Pribanic, N. Obradovic and J. Salvi, “Stereo computation combining structured light and passive stereo matching,” Optics Communications, vol. 285 issue 6, pp. 1017-1022, 2012.

• [3]    C. H. Lee, Y. C. Lim, S. Kwon and J. H. Lee, “Stereo vision–based vehicle detection using a road feature and disparity histogram”, Opt. Eng. vol. 50 issue 2, 027004, 2011.

• [4]    S. Belongie, J. Malik, and J. Puzicha., “Shape matching and object recognition using shape contexts,” IEEE Transactions on Pattern Analysis and Machine Intelligence, pp. 509-522, vol. 24 issue 4, 2002.

• [5]    H. A. Alnabriss, I. S. I. Abuhaiba, “Improved Image Retrieval with Color and Angle Representation,” I. J. Information Technology and Computer Science, pp. 68-81, vol. 6 issue 6, 2014.

• [6]    M. Z. Uddin, “A Two-Level Hidden Markov Model-based Approach for Human Activity Recognition,” I. J. Information Technology and Computer Science, pp. 21-29, vol. 17 issue 1, 2014.

• [7]    J. Shi and C. Tomasi, “Good Features to Track,” Proc. of the 9th IEEE Conference on Computer Vision and Pattern Recognition, pp. 593-600, 1994.

• [8]    K. Mikolajczyk and C. Schmid, “Scale & affine invariant interest point detectors,” Int. J. of Computer Vision, pp. 63-86, vol. 60 issue 1 , 2004.

• [9]    C. Schmid and R. Mohr, “Local gray value invariants for image retrieval,” IEEE Trans. on Pattern Analysis and Machine Intelligence, vol. 19 no. 5, pp. 530-534, 1997.

• [10]    D. G. Lowe, “Distinctive image features from scaleinvariant keypoints,” Int. J. of Computer Vision, vol. 60, no. 2 pp. 91-110, 2004.

• [11]    K. Sharma, S. G. Kim, and M. P. Singh, “An improved feature matching technique for stereo vision applications with the use of self-organizing map,” International Journal of Precision Engineering and Manufacturing, vol.13 issue 8, pp. 1359-1368, 2012.

• [12]    S. N Sinha, J. M. Frahm, M. Pollefeys and Y. Genc, “Feature Tracking and Matching in Video Using

  Programmable Graphics Hardware,” Machine Vision and Applications vol. 22 issue 1, pp. 207-217, 2011.

• [13]    K. Bjorke, “Image processing on parallel GPU pixel units”, Proceedings of SPIE, vol. 6065 (2006).

• [14]    J. Fung, S. Mann, and C. Aimone, “OpenVIDIA: parallel GPU computer vision,” Proc. of the 13th annual ACM international conference on Multimedia pp. 849-852, 2005.

• [15]    R. Yang and M. Pollefeys, “Multi-resolution real-time stereo on commodity graphics hardware,” Proc. of IEEE computer society conference on Computer vision and pattern recognition, pp. 211-217, 2003.

• [16]    C. Zach, H. Bischof, and K. Karner, “Hierarchical Disparity Estimation with Programmable 3D Hardware,” International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision, pp. 275288, 2004.

• [17]    M. Bramberger, B. Rinner, and H. Schwabach, “An embedded smart camera on a scalable heterogeneous multi-dsp system,” Proc. of the European DSP Education and Research Symposium, 2004.

• [18]    S. Klupsch et al., “Real Time Image Processing based on Reconfigurable Hardware Acceleration,” Proc. of IEEE Workshop on Heterogeneous Reconfigurable Systems on Chip, 2002.

• [19]    M. T. Jones and P. E. Plassmann, “Scalable iterative solution of sparse linear systems,” Parallel Computing vol. 20 issue 5, pp. 753-773, 1994.

• [20]    Y. Saad, “ILUM:   A Multi-Elimination ILU

  Preconditioner for General Sparse Matrices,” SIAM Journal on Scientific Computing vol. 17 issue 4, pp. 830847, 1996.

• [21]    T. Kohonen, “The self-organizing map,” Proc. IEEE vol. 78 issue 19, pp. 1464-1480, 1990.

• [22]    G. Toulminet et al., “Vehicle Detection by Means of Stereo Vision-Based Obstacles Features Extraction and Monocular Pattern Analysis,” IEEE Transactions on Image Processing, vol .15 issue 8, pp. 2364-2375, 2006.

• [23]    D. B. Kirk and W. W. Hwu, “Programming Massively Parallel Processors,” 1st edition, Morgan Kaufmann, Burlington, MA, USA, 2010.

  Author’s Profile

  
  
  

  Kajal Sharma received the B.E. degree in Computer Engineering from University of Rajasthan, India, in 2005, M.Tech. and Ph.D. degrees in Computer Science from Banasthali University, Rajasthan, India, in 2007 and 2010, respectively. From October 2010 to September 2011, she worked as a postdoctoral researcher at

  Kongju National University, Korea. From October 2011, she worked as a postdoctoral researcher at the School of Computer Engineering, Chosun University, Gwangju, Korea. Her research interest areas are image and video processing, neural networks,

computer vision, robotics, etc.