Градационные траектории как аналог градационных кривых в метрическом пространстве CIE Lab: дискретный подход
Автор: Тарасов Дмитрий Александрович, Мильдер Олег Борисович
Журнал: Компьютерная оптика @computer-optics
Рубрика: Численные методы и анализ данных
Статья в выпуске: 1 т.43, 2019 года.
Бесплатный доступ
В работе расширен подход, использующий трёхмерные градационные траектории в метрическом пространстве CIE Lab в качестве аналогов традиционных градационных кривых. Показано, что математический аппарат дифференциальной геометрии пространственных кривых, описывающий градационные траектории, может быть дополнен более простым дискретным подходом. Демонстрируются возможности применения дискретного метода вычисления градационных траекторий к задачам линеаризации цифровых печатных систем.
Линеаризация, градационные траектории, градационные кривые, цифровая печать
Короткий адрес: https://sciup.org/140243261
IDR: 140243261 | DOI: 10.18287/2412-6179-2019-43-1-132-136
Текст научной статьи Градационные траектории как аналог градационных кривых в метрическом пространстве CIE Lab: дискретный подход
В современной цифровой печати вопросы управления качеством стоят очень остро. Линеаризация цифровых печатных систем и обеспечение их предсказуемого отклика на управляющее воздействие со стороны растрового процессора (драйвера) и системы управления цветом с учётом выбранного набора «краска-бумага» являются основополагающими для обеспечения этого качества.
В предыдущих работах было введено понятие градационной траектории, которую можно назвать трёхмерной трактовкой градационных кривых в CIE Lab-пространстве [1, 2]. Исходной информацией для построения градационных траекторий является не оптическая плотность растрового поля, а Lab-координаты тестовых полей. Использование градационных траекторий позволяет произвести линеаризацию сразу по трём разным величинам: светлоте L , цветовому отличию ∆ E (или d E ) и цветовой координате.
В настоящий момент существует довольно большое число моделей предсказания цвета (МПЦ), призванных определить цветовой отклик печатной системы при использовании определённого типа краски на определённой подложке и в определённых условиях печатания и восприятия напечатанного. В эмпирических поверхностных моделях, учитывающих суперпозицию красочных полутонов, предполагается, что отражённый или прошедший свет является функцией эффективного покрытия поверхности красителями или базовых паттернов, образующих полутона красителя. Модели не описывают распространение и затухание света внутри оттиска и демонстрируют связь между отражённым светом и покрытием поверхности бумаги красителями. Физические модели включают более подробный анализ взаимодействия «свет-оттиск», основанный на математическом предсказании того, как проходят световые лучи в полутоновой печати и что происходит в результате их зату- хания. Модели распространения красителей предназначены для оценки эффективной поверхности точки краски после того, как она нанесена на запечатываемую поверхность при заданном номинальном покрытии этой поверхности. Разница между эффективным и номинальным поверхностным покрытием – это физическое увеличение (растискивание) точки, которое показывает, насколько физически расплывается краска. Модели распространения красителей, учитывающие все условия их суперпозиции, основаны на кривых тонового прироста (растискивания) краски, отображающих номинальные покрытия поверхности, на эффективные покрытия для полутонов одного цвета, а также наложений одной и двух сплошных плашек краски. Более современные модели предсказания цвета, такие как модели предсказания спектрального отражения, полезны при изучении влияния различных факторов (краска, подложка, условия освещения и воспроизведения полутонов), влияющих на диапазон отображаемых при печати цветов, а также на создание характеризационных профилей печатной системы для целей управления цветом [3]. Наиболее известные из них следующие: модель Кубелки – Мунка [4], предсказывающая свойства нескольких наложенных слоёв краски с учётом информации об отражении и непрозрачности каждой; модель Нейгебауэра [5], которая предсказывает трёхстимульные значения CIE XYZ цвета полутоновой плашки как суммы трёхстимульных значений её отдельных красителей; интегральная модифицированная модель Юла – Нильсена – Нейгебауэра [6, 7], в которой формула Юла – Нильсена применяется к спектральным уравнениям Нейге-бауэра. В литературе периодически появляются различные модификации и расширения указанных моделей, призванные уточнить результаты в условиях тех или иных несогласованностей [8]. Все предложенные подходы требуют существенного количества измерений, вычислений и проверок, однако, поскольку большинство из них основаны на эмпирических зависимостях, точность предсказания некоторых оттенков спектра отражения остаётся невысокой.
Предлагаемый метод градационных траекторий, напротив, достаточно прост, не требует громоздких вычислений и может быть успешно применён на практике. В данной работе продемонстрирована модификация метода градационных траекторий для линеаризации цифровых электрофотографических печатных систем.
1. Подход
Для начала определим понятие градационной траектории (ГТ). Примем, что ГТ – это геометрическое место точек в пространстве CIE Lab, координаты которых соответствуют результатам измерений Lab-координат отдельных полей (патчей) полутоновой шкалы, расположенных в порядке возрастания процента заполнения растровых ячеек в макете от 0% (незапечатанный субстрат) до 100% (полная заливка).
Полутоновые шкалы обычно содержат не более двух десятков полей, то есть на практике ГТ представлена дискретным набором точек в пространстве CIE Lab. Современные системы печати обеспечивают глубину цвета не менее 256 градаций (8 бит), то есть характеристики изменения цвета (оттенок, насыщенность и яркость), а также цветовые координаты могут рассматриваться как непрерывная функция процента (доли) заполнения растровой ячейки. Другими словами, мы можем ожидать почти непрерывного изменения цветовых характеристик при постоянном изменении процента заполнения растровой ячейки.
Если взять процент заполнения растровой ячейки как некий параметр t кривой, то ГТ может быть задана параметрическими уравнениями:
' t е [0; 1], a = a 4t4 + a 3t3 + a 2t2 + a1 t + a 0, b = b 4t4 + b 3t3 + b 2t2 + b 1 t + b 0,
L = (L о - L ») ■ exp (—L з t3 — L 2t2 — L11) + L » , где Li, ai, bi i = 1..4 - некоторые числовые коэффициенты, (L0, a0, b0) – Lab-координаты незапечатанной подложки, Lж - визуальная яркость гипотетического сплошного красочного слоя бесконечной толщины. Интервал изменения параметра t от 0 (незапечатанная подложка) до 1 (100% заливка). Формулы (1) для a и b координат, по сути, есть разложение функций координат в ряд Тейлора вблизи точки, соответствующей запечатываемой подложке. L-координата является убывающей функцией на отрезке, ограниченной сверху (бумага – самый яркий объект) и снизу («банка с краской» – самый тёмный объект). Поэтому её описание убывающей экспонентой представляется разумным.
Вводя таким способом ГТ, мы подразумеваем, что ни один реальный полиграфический краситель (краска, тонер или чернила), за исключением, быть может, черного, не должен быть доведён до такой оптической плотности, что Lab-координаты получаемого цвета достигнут точки сингулярности Lab-простран- ства (Y/Y0 < 0,008856. Это соответствует, например, ситуации, когда средний коэффициент отражения образца цвета менее 1 %). В любом случае этот участок ГТ должен быть исключён путём ограничения подачи красителя при настройке печатной системы. В противном случае автотипный цветосинтез, основанный на представлении о прозрачных красителях, представляется затруднительным.
Ранее [9] была исследована возможность применения ГТ для линеаризации струйного принтера. Струйная печать предполагает возможность ограничения подачи чернил на уровне RIP (растрового процессора). В качестве критерия ограничения был предложен и экспериментально опробован максимум кривизны ГТ, т.е. точка, после которой начинается резкое изменение цветового тона и/или визуальной яркости. В настоящей работе мы покажем возможности ГТ для линеаризации электрофотографических цифровых печатных машин (ЦПМ).
Технология электрофотографической (ЭФ) печати не предполагает возможности для оператора регулировать максимум подачи тонера. Изменить количество тонера в случае сплошной (т.н. «плашечной») заливки можно лишь изменяя предварительный заряд фоторецептора и/или мощность системы экспонирования – лазер или светодиодная линейка [10]. Следовательно, в данном случае нет необходимости вычисления кривизны ГТ. Более того, именно для ЭФ-машин наиболее характерна глубина цвета в 8 бит на цветовой канал, т.е. функции (1) оказываются представленными дискретным набором из 256 значений.
С другой стороны, дискретность возможных значений параметра тона t никоим образом не отменяет предположение о непрерывности функций координат цвета. Если изменить настройки экспонирования ЦПМ, то при том же значении аргумента тона t координаты цвета несомненно изменятся, но останутся в пределах траектории, т.к. ГТ есть инвариант печатной системы для данной пары «бумага-тонер».
Таким образом, в случае ЭФ-печати представляется оптимальным пересчитать приращение тона при дискретном приращении параметра t в формулах (1), используя любую формулу цветового отличия. В [9] была использована NE 94 потому, что NE 2000 весьма сложно представима в виде дифференциала. В случае дискретного задания параметра t ограничение на использование формулы NE 2000 снимается.
2. Эксперимент
В качестве печатной системы использовалась ЭФ ЦПМ Konica Minolta Bizhub Pro C6000L, бумага Moorim Neo Star Matt 140 г / м2.
Алгоритм эксперимента следующий. Создание и печать тестовой шкалы → Измерение Lab-координат полей спектрофотометром → Сортировка данных протокола измерений по цветовым каналам в порядке увеличения процента заполнения → Аппроксимация функций координат (1) → Расчёт цветового отличия на каждый «квант» приращения тона → Расчёт длины ду- ги ГТ в единицах цветового отличия AE2000 от 0 до 100% приращения тона в макете → Разделение кривой на сегменты равной длины → Определение оптимальных значений тона в макете, разделяющих дугу ГТ на сегменты равной длины → Печать и измерение исходной шкалы с «исправленными» значениями тона.
Тестовые градационные шкалы были синтезированы с помощью ChartGenerator в пакете MeasureTool ProfileMaker для автоматического спектрофотометра i1 iSis. Рецептура тестовых полей была округлена до 8-битного целого. Так, например, поле 50%-й заливки имело фактическую рецептуру 50,196% (подробней см.: Результаты и обсуждение). Математическая обработка производилась в MS Excel и среде Matlab.
Тест содержал 14 последовательно повторяющихся комплектов градационных шкал, равномерно распределённых по площади печатного листа. Результаты измерений сохранялись в виде текстового файла, который затем импортировался в MS Excel, где данные делились на отдельные цветовые каналы. Матричные переменные, содержащие данные t , L , a , b каждого цветового патча в качестве столбцов, импортировались в Matlab, где обрабатывались посредством специально написанных функций.
3. Результаты и обсуждение
Следует отдельно обсудить принцип формирования тестовых шкал. В рассмотренных экспериментах использовались градационные шкалы с ~ 5% приращением тона в макете от 0 до 100%. Однако ЦПМ имеет ограниченный набор (255) способов формирования тоновых комбинаций на каждый цветовой канал. Это должно быть учтено на этапе формирования шкалы. Значение параметра t должно быть задано без систематической погрешности. Так, если предполагается, что доля тона должна принимать значения из ряда [0; 0,05; 0,1… 0,95; 1], то с учётом возможностей печатной системы (8 бит) значения ряда должны быть преобразованы по формуле:
t fact = unit8 ( t des x 255 ) /255, (2) где t des – желаемая доля тона, t fact – фактически реализуемая доля тона, uint8 – функция Matlab для округления до целого числа в диапазоне 0–255 (8-битного целого).
Аппроксимация экспериментальных данных зависимостями (1) реализовалась в пакете Matlab с использованием функции fit . Качество аппроксимации оценивалось как среднее отличие AE 2000 данных экспериментального протокола от значений, полученных расчетом по (1), при равных значениях параметра t . Среднее отличие составило 0,6-0,8 единиц A E 2000 для разных цветовых каналов, что совпадает с величиной среднего цветового отличия полей одинаковой рецептуры.
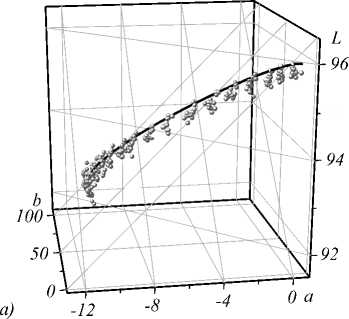
На рис. 1 в качестве примера показаны градационные траектории для цветовых каналов Yellow и Black в пространстве CIE Lab. Точки на графиках соответствуют результатам измерения градационных шкал, сплошные кривые являются аппроксимирующими градацион- ными траекториями. Как следует из рисунков, погрешность аппроксимации может быть целиком отнесена на счёт погрешностей печати и измерения.
Ранее [1] было обнаружено, что для струйной печати характер взаимодействия «краска-бумага-свет» настолько нелинейный, что ГТ обладает кручением, зависящим от параметра тона t . Ограничение подачи чернил в процессе линеаризации позволяло минимизировать кручение ГТ, т.е. линеаризованный участок ГТ можно было считать плоским. Как уже отмечалось, в случае ЭФ-печати ограничение подачи тонера не предусматривается на уровне оператора ЦПМ. Это означает, что ГТ в случае ЭФ-печати в общем случае не является плоской кривой и не может быть сведена к таковой. Это хорошо видно на примере чёрного канала (рис. 1 б ). Следовательно, использование полиномов четвёртой степени в формулах (1) вполне оправдано.
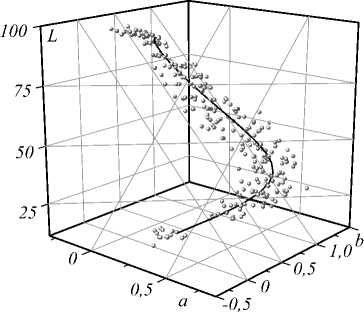
Рис. 1. ГТ для каналов Yellow (а) и Black (б)
На рис. 2 показан характер приращения цветового отличия в зависимости от приращения тона в макете до и после линеаризации для цветовых каналов Yellow и Black. После проведения линеаризации приращение тона для любого цветового канала описывается линейной зависимостью с коэффициентом детерминации не менее 0,99.
Характерной особенностью ЭФ-печати является сигмоидальный характер «классических» градационных кривых [10]. Как видно из рис. 2, этот же характер имеет зависимость приращения цветового отличия до линеаризации (см. маркеры 1 на рис. 2). Предложенный метод линеаризации успешно корректирует этот эффект.
б)
Выводы
В работе предложена модификация градационных траекторий как трёхмерной интерпретации градационных кривых в CIE Lab-пространстве, учитывающая дискретность формирования цветового тона в ЦПМ. ГТ рассматриваются как непрерывные, ограниченные на заданном отрезке кривые, описываемые при помощи аппарата дифференциальной геометрии кривых. Модификация метода заключается в рассмотрении непрерывных функций в сочетании с дискретным аргументом. Дискретность аргумента обусловлена технологией ЭФ-печати.
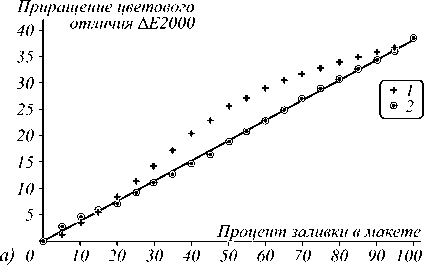
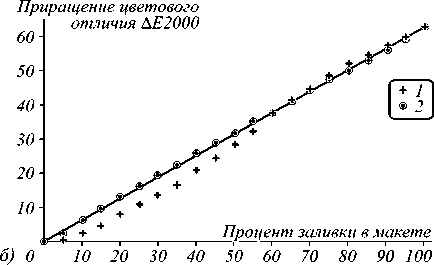
Рис. 2. Цветовое различие CIE Lab ΔE2000 между патчами, соответствующими увеличению тона на 0,05 до (1) и после (2) линеаризации для цветовых каналов Yellow (а) и Black (б)
Градационные траектории, введённые описанным образом, являются глобальными характеристиками печатного процесса, зависящими только от типа запечатываемой подложки и свойств красителей. На них не влияют метод растрирования и методика измерений.
В связи с дискретностью задания аргумента, приращение длины дуги кривой ГТ может быть непосредственно просчитано для каждого «кванта» приращения тона. Дискретность аргумента значительно упрощает и ускоряет процесс линеаризации печатных систем, т.к. в этом случае отсутствует необходимость численного решения интегро-дифференциальных уравнений, что использовалось в [9].
Дальнейшая разработка подхода предполагает внедрение 3D-градационных поверхностей в качестве метода, описывающего взаимосвязь между двумя красителями, особенно в случае пар регулярных и осветлённых чернил в струйной печати (C–LC, M–LM).
Список литературы Градационные траектории как аналог градационных кривых в метрическом пространстве CIE Lab: дискретный подход
- Титова, М.Ю. Градационные траектории: получение и анализ/М.Ю. Титова, О.Б. Мильдер, Д.А. Тарасов. -В кн.: Информация: передача, обработка, восприятие. Материалы международной научно-практической конференции/под ред. А.Г. Тягунова, А.П. Сергеева. -Екатеринбург: УрФУ, 2016. -С. 120-125.
- Milder, O.B. Inkjet printers linearization using 3D gradation curves/O.B. Milder, D.A. Tarasov, M.Yu. Titova//CEUR Workshop Proceedings. -2017. -Vol. 1814. -P. 74-83.
- Bala, R. Device characterization/R. Bala. -In Book: Digital color imaging handbook/ed. by G. Sharma. -Boca Raton, FL: CRC Press, 2003. -P. 269-379.
- Kubelka, P. Ein Beitrag zur Optik der Farbanstriche/P. Kubelka, F. Munk//Zeitschrift für technische Physik. -1931. -Vol. 12. -S. 593-601.
- Neugebauer, H.E.J. Die theoretischen Grundlagen des Mehrfarbendrucks/H.E.J. Neugebauer//Zeinschrift fur Wissenschaftliche Photographie, Photophysik und Photochemie. -1937. -Vol. 36. -S. 36-73.
- Yule, J.A.C. The penetration of light into paper and its effect on halftone reproductions/J.A.C. Yule, W.J. Nielsen//Proceedings of the 1951 Technical Association of Graphical Arts. -1951. -Vol. 3. -P. 65-76.
- Viggiano, J.A.S. Modeling the color of multi-colored halftones/J.A.S. Viggiano//Proceedings of the 1990 Technical Association of Graphical Arts. -1990. -P. 44-62.
- Никоноров, А.В. Построение адаптивной системы управления цветовоспроизведением с распознаванием опорных областей цветового пространства/А.В. Никоноров, В.А. Фурсов//Компьютерная оптика. -2008. -Т. 32, № 3. -С. 290-295.
- Milder, O. Ink-jet printer’s characterization by 3D gradation trajectories on an equidistant color difference basis/O. Milder, D. Tarasov. -In: Image and video technology/ed. by M. Paul, C. Hitoshi, Q. Huang. -Cham, Switzerland: Springer International Publishing AG, 2018. -P. 40-52. - DOI: 10.1007/978-3-319-75786-5_4
- Cousoulis, M. Electrophotography/M. Cousoulis. -In: Handbook of digital imaging/ed. by M. Kriss. -Hoboken, US: John Wiley and Sons Ltd, 2015. -Vol. 2. -Chap. 19. -P. 759-810.


