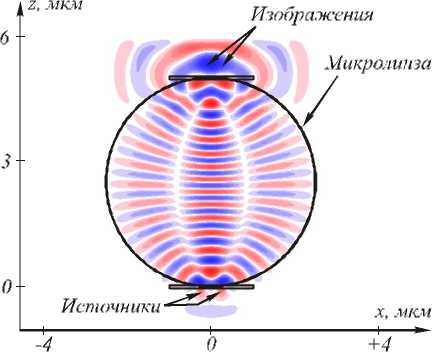
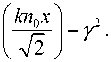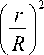Градиентные элементы микрооптики для достижения сверхразрешения

Фокусировать когерентный лазерный свет в пятно меньшее дифракционного предела или изображать точечный источник света со сверхразрешением стало возможно в последние годы с развитием микрооптики и нанофотоники. Преодолевать дифракционный предел, равный 0,51 λ/n , где λ – длина волны света в вакууме, n – показатель преломления вещества в месте фокуса, можно с помощью суперлинз [1]. Суперлинза – это 2D плоская пластина из метаматериала, который представляет собой чередующиеся субволновые слои металла и диэлектрика. Диэлектрические проницаемости таких слоев подбирают таким образом, чтобы эффективный показатель преломления композитного вещества был равен n = -1. Эксперименты по сверхразрешению с помощью такой линзы были осуществлены в [2, 3]. В эксперименте было достигнуто сверхразрешение, равное 0,4 λ [2]. Аналогичный эксперимент был проведен в [4] с помощью субволнового слоя серебра, который также работает как суперлинза. В этой работе были разрешены две линии, разделенные расстоянием 145 нм при освещении их ультрафиолетовым светом с длиной волны 365 нм. То есть в [4] было также достигнуто сверхразрешение, равное 0,4 λ .

В [5] была реализована гиперлинза, которая изображает со сверхразрешением в дальней зоне. При этом были разрешены две линии шириной по 35 нм, разделенные расстоянием 150 нм, с помощью света с длиной волны 365 нм. То есть опять было достигнуто сверхразрешение равное 0,4 λ. Хотя при моделировании гиперлинзы в виде решетки в [6] было получено сверхразрешение равное 0,05λ на расстоянии 1,5λ от поверхности. По-видимому, при моде- лировании не учитывается поглощение и рассеяние света метаматериалом, которое имеет место в реальных экспериментах. Это косвенно подтверждают результаты работы [7]. В [7] исследовалась фокусировка лазерного света с помощью зонной пластинки из золотой пленки толщиной 100 нм. Расчет показал, что диаметр фокусного пятна по полуспад у интенсивности должен быть равен 0,35λ, а в эксперименте было получено, что диаметр фокусного пятна по полуспад у интенсивности равен λ.

В [8-10] численно анализируются многослойные и анизотропные наноструктуры , которые позволяют получить субволновое разреш ение. Так, в [8] подобраны параметры 8-ми слойной 1D структуры на основе Ag/SiO 2 , которая имеет толщину 400 нм и изображает источник шириной 0,4 λ в световое пятно такой же ширины. В [9] предложена анизотропная 2D наноструктура, у которой составляющие тензора диэлектрической проницаемости имеют значения ε x = 0,01- i 0,01 и ε z = -100, а толщина структуры вдоль оси z равна 400 нм (длина волны λ = 700 нм). Моделирование показало, что такая структура разрешает две линии толщиной по 3 нм, разделенные расстоянием 23 нм. То есть было достигнуто сверхразрешение, равное 0,03 λ . В [10] теми же авторами предложена другая 2D наноструктура, состоящая из двух разных анизотропных слоев, которая разреш а-ет две узкие щели, разделенны е расстоянием 50 нм, при освещении их светом с длиной волны 1550 нм.

Еще одним кандидатом на достижение сверхразрешения являются фотонные кристаллы. В [11] с помощью моделирования показано, что 2D фотонно-кристаллический слой из диэлектрика с проницаемостью ε = 12 и треугольной решеткой круглы х отверстий с радиусом r = 0,4a, а – период решетки отверстий, имеет эффективный показатель преломления n = -1 и является изображающей линзой для длины волны λ = a/0,3. При этом точечный источник изображается в виде пятна диаметром по полуспаду интенсивности, равным 0,3λ, а два точечных источника разреш аются по критерию 20%, если расстояние межд у ними равно 0,5λ.

В недавно проведенных экспериментах по использованию 2D фотонно-кристаллического слоя в качестве суперлинзы было получено изображение точечного источника шириной 0,4 λ [12]. Появились также работы, в которых предлагается усовершенствовать суперлинзу с помощью специальной наноразмерной оболочки [13] или с помощью градиентной границы для слоя вещества с отрицательной рефракцией [14]. В [15] экспериментально продемонстрировано, что слой анизотропного вещества способен усиливать и преобразовывать поверхностные неоднородные волны в распространяющиеся световые волны.

В данной работе численно показано, что хорошо известные в оптике градиентные линзы Микаэляна и «рыбий глаз» Максвелла также могут рассматриваться как кандидаты на получение изображений со сверхразрешением. Для 2D микролинзы Микаэляна показано, что точечный источник света изображается вблизи поверхности линзы в виде светового пятна с шириной по полуспаду интенсивности FWHM = 0,12λ. Это меньше, чем дифракционный предел для кремния (n = 3,47): 0,5λ/n = 0,144λ, и меньше, чем сообщалось в работах [7, 8, 11, 12]. Также показано, что микролинза Микаэляна разрешает по полуспаду два близких точечных источника, разделенных расстоянием 0,3λ, что меньше, чем сообщалось в работах [2, 4, 5, 11].

В [16,17] получены ан алитические соотношения для расчета мод в градиентном планарном волноводе. В [16] на основе аппроксимации непрерывной функц ии показателя преломления градиентного волновода кусочно-постоянной функцией и на основе применения метода передаточных матриц записаны рекуррентные уравнения для поиска неопределенных постоянных локальных мод в каждом слое с постоянным показателем преломления. В [17] на основе модифицированных функций Эйри и метода ВКБ получены уравнения на собственные значения для расчета параметров модовых функций градиентной среды. Общим ограничением в этих работах является предположение о н аличии одной [16] или двух [17] точек возврата, которые имеет ф ункция распределения показателя преломления планарного волновода.

В данной работе получены более общие аналитические выражения для модовых решений в планарном волноводе без ограничений на число точек возврата в ф ункции показателя преломления.

1.    Решение уравнения Гельмгольца для 2D градиентного волновода

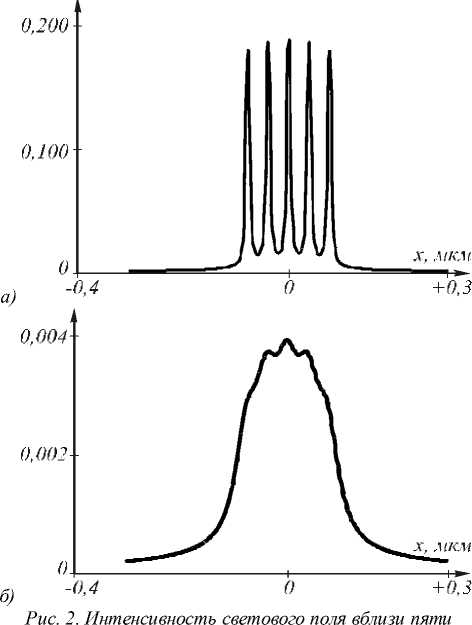
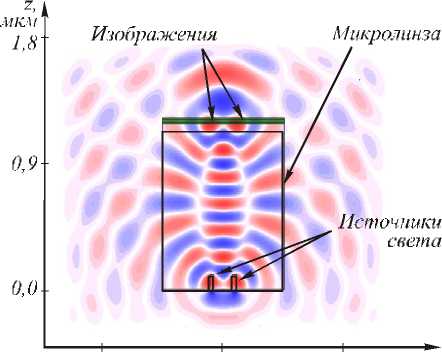
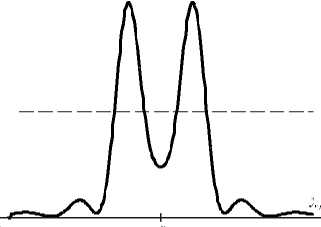
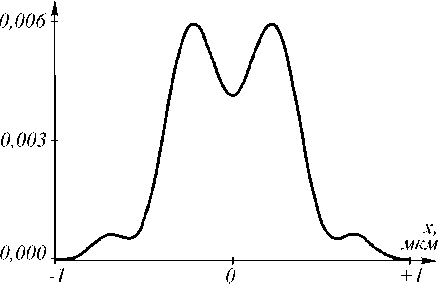
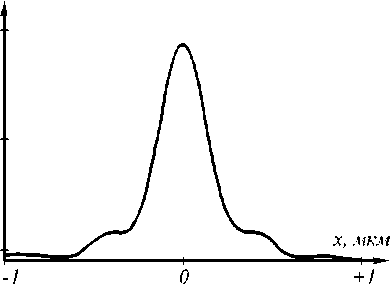
На рис. 1 показана схема задачи. Рассмотрим градиентную двумерную сред у с показателем пре- ломления n = n(x), в которой распространяется электромагнитная волна с ТЕ- поляризаци ей, вектор напряженности электрического поля которой направ-

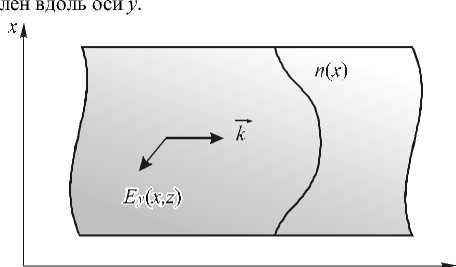
Рис. 1. Схема задачи распространения ТЕ-поляризованной волны в 2D градиентном волноводе

Амплитуда электрического вектора E y (x,z) удовлетворяет уравнению Гельмгольца [18]:

d2 'J2 .       2r

2 + 2 + k n ( x ) о x   о z

E y ( x , z ) = 0,

где k – волновое число. Разложим амплит уд у электромагнитной волны по поперечным модам градиентной среды:

^

Ey (x, z) = E Cn (x) exP(i^nz) , n=0

где β n = k zn – постоянная распространения n -ой моды. Из представления (2) след ует, что у светового поля имеется продольный период T , так что β n = 2πn/T . Например, для градиентной среды с квадратичной зависимостью показателя преломления модами являются функции Эрмита-Гаусса, составляющие счетный базис [19].

Подставляя (2) в (1), получим уравнение для амплитуды мод градиентной среды:

d ² C ( x )

• -2 + P n ( x ) C n ( x ) = 0, dx

где

P n ^{( x} ) = k ² n ^{2 ( x} ) - Д 2 .

Заменой переменных

C n ( x ) = C n (0)exp j f n ( ^ ) d §

_ 0

уравнение (3) сводится к нелинейному дифференциальному уравнению Уиттекера [20] для функции f n (x) :

df n Tx) ⁺ f n ^{2( x}) ⁺ P n ^{( x}) = 0. dx

Уравнение (6) может быть решено с помощью разложения в ряд Тейлора ф унк ций f n (x) и p n (x) :

^

f n ( x ) = e C mn) x'

m = 0

^

Pn(x)=e pmn) x m =0

m ,

m ,

где C_m n ) и p ^n ) неизвестные и известные коэффици

енты разложения соответствующих функций. Подставляя (7) и (8) в (6), для неизвестных коэффициентов ряда (7) получим рекуррентные соотношения ( m > 0):

С ( n ) ₌ __т^-1 1 „( n )       _Г( n )_Г( n ) I

C m = ^m I p m -1 ⁺ A C s C m -1- s I ,                 ⁽⁹⁾

V         s = 0              )

где n - положительное целое число, C 0 n ) - неопределенные константы. Тогда для амплитуд мод градиентной волноводной среды можно записать явное выражение:

( ^          m+ +1 ]

C n ( x ) = C n (0)exp I A C mn )----- I ,

I m -",      m + 1 )

в котором C_m ^{( n )} находятся из рекуррентны х соотношений (9). Коэффициенты p mn ) , входящие в (8) и (9), находятся по формулам:

( n )     k ² d^mn ² ( x )

Pm ⁼ ~[ J m m ! dx ^m

x =0

при m > 0 и при m = 0 из соотношений p 0 ⁿ ) = к ² n ²(0) - д ².

Окончательное выражение для амплитуды светового поля ТЕ-поляризованной волны в градиентной 2D среде имеет вид:

га

Ey (x, z) = A Cn (0) eXP n=0

ra i^nZ +1 Cmn)

m =0

x m +1

m + 1

В (13) для каждой моды имеются две неопределенные константы C_n ( 0 ) и C 0 ⁿ ) . Моды (10) не яв-

га

E y ^{( x} , z ) = A ^C n i°>^exp n = 0

Решение (16) представляет собой хорошо известное решение уравнения Гельмгольца (1) в виде суперпозиции плоских волн.

2) Рассмотрим другой частный    случай:

n ² ( x ) = n 2 - а ² x ² - квадратичная среда. В этом случае ( n )         ( n )           ( n ) 2                           ( n )         2 2         2

p n ^{( x} ) = p 0 ^{+ p x +} p 2 ^x , где p 0 = ^kn 0 ^- P n , p ^{( n} ) = 0, p 2 ⁿ ) =- к ² а ² и p mn ) = 0 при m > 2. Пусть C 0 ⁿ ) = 0, тогда C 2 ⁿ ) =- ( C 0 ⁿ ) Г ⁿ ) ) = 0, а C 1^{( n} ) = - p 0 ⁿ ) = в - к ² n 2 . Чтобы все остальные коэффициенты были равны нулю C_m ^{( n )} = 0 при m > 2, достаточно положить равным нулю третий коэффициент: C ₃ ^{( n} ) = - p 2 ⁿ ) / 3 - ( C 1^{( n} ) ) ² / 3 = 0 . Тогда на параметр среды а получим условие: к ² а ² = ( к ² n 2 - Д 2 ) ² ■ Положим P_n = -и ₀ /V2 , тогда получим, что а = ки 2 / 2 . Итак, получается, что модой квадратичного волновода с показателем преломления n ² ( x ) = n 0 ( 1 - к ² n 0 x ²/ 4 ) является гауссовая экспонента:

222 II

Ey,(x,z) = C(0)expI --^2---40— I.(17)

В заключении этого раздела отметим, что так как производная в нуле модовой функци и (10) пропорциональна нулевому коэффициенту в ряде (7):

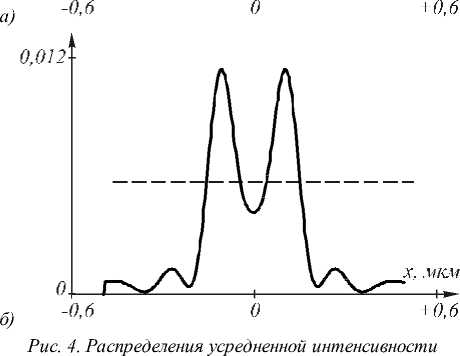
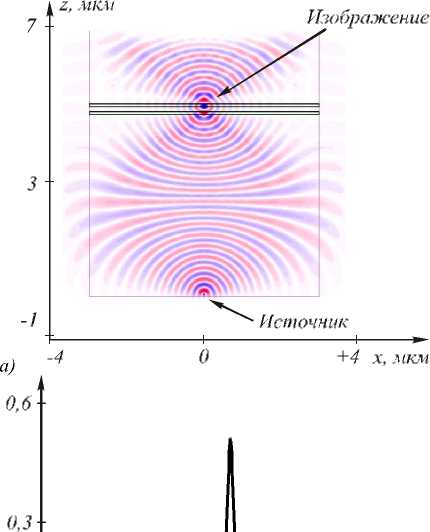
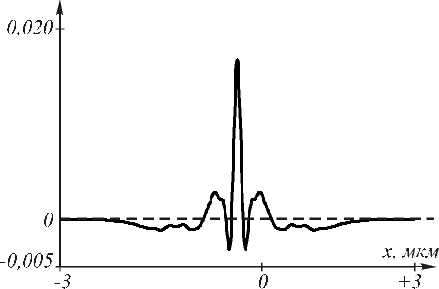
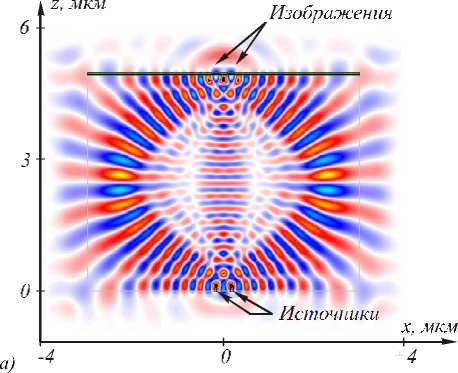
dCn^xl I = c (0)C

J„ I x =0 nV 7 0 ,

ГiPn-^{+ -}xV^-2n^{2 - e}n 1. ⁽¹⁶⁾

ляются ортогональными и нормированными, поэтому для разложения поля (13) по этим модам (то есть нахождения коэффициентов C_n (0)) потребуется усечение обоих рядов в (13) до конечных сумм и решение системы линейных алгебраических уравнений.

Постоянные C₀⁽ⁿ⁾для каждой моды нужно выбирать специальным образом. Для примера рассмотрим два частны х случ ая.

1) Пусть n(x) = n₀ и моды распространяются в однородном пространстве. Из (11) и (12) получим, что p0ⁿ) = к²n²(0)-в при m = 0 и pmn⁾= 0 при m > 0. Из (9) следует, что

то выбором C₀⁽ⁿ⁾= 0 (как это было сделано в последнем примере) обеспечивается наличие экстремума у моды на оптической оси.

2. Общее решение для секонс-градиентного волновода

Для градиентного волновода с секонсной зависимостью показателя преломления от поперечной координаты

n (x) = n₀ ch ¹

-п₀x

V2

известно частное решение уравнения (1) след ующе-го вида [21]:

C1n) =-(p0n) + (C*ⁿ))²).                            (14)

\       Г^--по^{- 1} k-1 Г^kno^{x 1}

E1 _y (x, z) = exp I ^- ) ch I ^- ) .            (20)

Пользуясь произволом в выборе C₀⁽ⁿ⁾, положим:

Уравнение Гельмгольца (1) в этом случае имеет

n⁽n)

C 0

=^-\ A=iA

n²

A².

Тогда из (14) следует, что C₁⁽ⁿ⁾= 0 , а из (9) следует, что и все остальные коэффициенты равны нулю: C_mn) = 0 при m > 0. Итак, для однородного пространства n(x) = n₀ вместо (13) получим:

вид:

^д_ ^д_ .,22 . -2 Г^^x

—Т I I -п₀ ch dx²дz^{2      0}I V2

Ey (x, z) = 0 .

Будем искать общее решение (21) в виде

E1 y (x, z) = A(x) exp(iyz).                         ⁽²²⁾

Подставляя (22) в (21), получим уравнение

d²A(x)

. 2⁺g⁽x) ^{A (}x) = 0, dx

где

Подставляя (32) в (31), получим уравнение: (-2 q²- p²+ k²n₀²+ 4 q⁴x²- w²k²n 2 x²)x xE₀ exp (ipz - q²x²) = 0.

g (x) = k²n0 ch ²

Из (33) определим неизвестные параметры:

₂wkn₀ q = ~,

w p = knn. 1--

⁰kn₀

.

Известно [20], что уравнение вида (23) имеет общее решение

Таким образом, частное модовое решение уравнения (31) имеет вид:

A( x) = A (x)

x

C + C2 J A Ao d^

I Г

E₂ (x, z) = E_o exp ikn_tiz 1

I

w kn0

wkn_{0 2}

2 x

I

. (34)

где A1(x) – частное решение (23), C1 , C2 – неопределенные константы. В нашем случае в качестве частного решения может быть выбрано решение (20), то есть

Заметим, что при w = kn0/2 решение (34) совпадает с решением (17). При w = kn0/2 из (34) следует, что ширина (диаметр) гауссовой моды по полуспаду

A (x) = ch ¹

kn₀x

kn

Y = Г2

.

интенсивности равна:

FWHM = ^n^² = ⁿⁿ 0

0.382

n₀

Тогда общее решение для моды секонс-

градиентного волновода будет иметь вид:

Г i \ I iknoz I

E1 y (x, z) = exp I ^2 I ch

₄1 kn_ox I

—x

I A2 )

x 0 C1 +

C2 kn₀ 2

1              kn x

— sh( kn₀xV 2) + ^

где

।              ।           dE. (x = 0, z)

C = Eiy (x = 0, z) , C2 = —^------

Из (20) можно получить выражение для ширины

моды по полуспад у интенсивности в секонс-

Сравнивая (35) с (29), видим, что ширина обеих мод (секонсной и гауссовой) почти одинаковая. Эффективная ширина квадратичного волновода находится из условия n(x0) = 1 и равна

27 n о -1

2x₀ =     ---2 .                             (36)

ⁿⁿ0

При n0 = 1,5 из (36) получим: 2x0 ≈ 0,48λ. То есть эффективная ширина стеклянного планарного волновода с квадратичной зависимостью показателя

преломления, в котором может распространяться только гауссовая мода (34), почти равна половине длины волны света в вакууме. Заметим, что такие «полуволновые» волноводы в настоящее время активно используются в приложениях [22, 23].

градиентном волноводе:

FWHM =

ln(3 + 272)₌0,42 nn₀72      n 0 ’

где λ – длина волны света в вакууме, n0 – как и пре- жде, показатель преломления на оси волновода.

• 3.    Частное решение для квадратичного волновода

В первом разделе данной работы показано, что для квадратичной среды с определенными параметрами модой является гауссовая экспонента (17). В этом разделе покажем, что это остается верным и для квадратичной среды с произвольными параметрами:

n²( x) = n 0 (1 - w²x²),

где w – произвольная постоянная. Тогда уравнение (1) будет иметь вид:

д² д²      . .

. +    + k n 0(1 - W x ) Ey ( x , Z ) = 0, д x   дz

а его решение б удем искать в виде:

E2_y (x,z) = E₀ exp (ipz- q²x²).                  (32)

• 4.    Моделирование прохождения света через градиентные элементы микрооптики: сверхразрешение

• 4.1.    Сверхразрешение с помощью микролинзы Микаэляна

Несколько лет назад были проведены эксперименты по сверхразрешению в оптическом диапазоне с помощью суперлинз [3,5]. В [3] в качестве суперлинзы использовался тонкий слой серебра толщиной 50 нм. Эксперимент состоял в получении изображения со сверхразрешением в слое резиста амплитудной решетки с периодом 145 нм вблизи тонкой пленки серебра. После освещения ультрафиолетовым светом с длиной волны 365 нм трехслойной структуры (амплитудная решетка + пленка серебра + резист) и после проявления, в слое резиста «записывалась» и была восстановлена с помощью преобразования Фурье решетка с периодом 170 нм. В [5] была реализована гиперлинза, представляющая собой полуцилиндр с кольцевым вырезом на подложке из кварца, состоящий из черед ующихся слоев серебра (толщиной 35 нм) и диэлектрика Al2O3 (толщиной 35 нм). Такая многослойная структура имеет анизотропную диэлектрическую проницаемость. Объектом разрешения служили две амплитудны е линии, полученные литографическим способом, имеющие ширину 35 нм и разделенные расстоянием 150 нм. Этот объект освещался ультрафиолетовым светом с ТЕ-поляризацией и длиной волны 365 нм. С помощью обычной линзы было получено увеличенное изображение этих двух линий, разделенных уже расстоянием 350 нм. Таким образом, в описанных экспериментах [3,5] было достигнуто сверхразрешение равное 0,4λ.

Теоретически (без учета поглощения материала) с помощью суперлинзы может быть достигнуто любое разрешение . Так, в [9] с помощью моделирования показано, что гиперболическую линзу, формирующую в ближнем поле увеличенно е субволновое изображение, можно реализовать и в виде плоскопараллельного слоя. Было показано, что слой анизотропного вещества с диэлектрическими проницае-мостями εx = 0,01-i0,01 и εz = -100 толщиной 400 нм разрешает две щели шириной по 3 нм (вытянутые вдоль оси y) в металлическом экране с диэлектрической проницаемостью ε = 1-i10⁴, разделенных расстоянием 23 нм, если осветить их светом с ТМ-поляризацией и длиной волны 700 нм. Величину сверхразрешения можно оценить как 0,05λ.

В следующих подразделах будет численно показано (хорошо известным методом FDTD), что с помощью градиентной 2D микрооптики также можно достичь сверхразрешения. Моделирование проводилось с помощью программы FullWAVE фирмы RSoft (США).

гауссовых источников света шириной λ/200, разделенных интервалом λ/50 на разных расстояниях: z = 5 нм (а), z = 30 нм (б), λ = 1550 нм (по оси ординат отложены произвольные единицы)

Из-за дифракции света в однородном пространстве два близких точечных источника света пере- стают разрешаться на расстоянии много меньшем длины волны. Так, на рис. 2а показаны исходные (в плоскости z = 5 нм) пять гауссовых когерентных источников света шириной λ/200 каждый, которые разделены расстоянием λ/50. На рис. 2б показана интенсивность света от этих источников на расстоянии z = 30 нм для длины волны λ = 1550 нм. Из рис. 2 видно, что близкие точечные источники пере- стают разрешаться на расстоянии, примерно равном промежутку межд у ними (z = λ/50).

На рис. 3 показан результат моделирования формирования изображения двух точечных источников света (ширина каждого из них по 35 нм), разделенных расстоянием 150 нм, с помощью линзы Микаэляна [24, 25].

Показатель преломления такой   секонс- градиентной 2D микролинзы имеет вид:

-1              ()             \ i x, мкм

Рис. 3. Схема расположения 2D градиентной микролинзы Микаэляна в окне программы FullWAVE для моделирования изображения двух близких точечных источников света. Показана мгновенная амплитуда Ey(x,z) в момент времени, когда свет прошел расстояние в 18,2398 мкм

n (x) = n 0 ch ¹

nx

2L

где 2L – длина линзы. Ширина линзы 2R находится из условия, что n(R) = 1. Для линзы на рис. 3 показатель преломлен ия на оси n₀ = 2,1, ширина линзы 2R = 1 мкм, длина линзы 2L = 1,144 мкм, длина волны λ = 365 нм. Выбранные парам етры совпадают с параметрам и эксперимента в работе [5].

На рис. 3 показана мгновенная картина амплитуды электрической составляющей электромагнитной волны с ТЕ-поляризацией (свет распространяется на рис. 3 снизу вверх). Видно, что на противоположной по отношению к источникам света стороне линзы формируется их изображение. На рис. 4а показано распределение усредненной по времени интенсивности электрического поля I(x, z = z0) = | Ey (x, z = z0 )|

непосредственно на «задней» стороне линзы, то есть на расстоянии z0 = 2L от «передней» стороны линзы. Два источника света находились перед «передней» стороной линзы на расстоянии 20 нм.

0,035

X, мкм

О

электрической составляющей ТЕ-поляризованной световой волны, рассчитанные на расстоянии z = 0 (а) и z = 10 нм (б) от «задней» поверхности линзы Микаэляна (рис. 3), на входе у которой расположены два близких точечных источника света (горизонтальная линия делит интенсивность по полуспаду, по оси ординат отложены произвольные единицы)

Из рис. 4а видно, что два точечных источника, разделенных расстоянием 150 нм (межд у центрами источников 180 нм), уверенно разрешаются. Если плоскость регистрации интенсивности уд алить от «задней» плоскости линзы на расстояние z = 10 нм (рис. 4б), то источники продолжают разрешаться, хотя величина «провала» в распределении интенсивности слегка уменьшается. Величина разреш е-ния, достигнутая на рис. 4, равна 0,41λ. Из рис. 4а можно также определить, что ширина изображения линзой Микаэ ляна точечного источника по полуспад у интенсивности равна FWHM = 100 нм = 0,27λ. Полученное значени е величины разрешения 0,41λ почти равно разрешению, полученному в [2,3,5] (0,4λ). Заметим, что полученная ширина изображения 0,27λ точечного источника согласуется с минимальной шириной моды, способной распространяться в секонс-градиентном волноводе 0,4λ/n0 = 0,27λ при n0 = 1,5 (см. ур. (29)).

С целью увеличения разрешения линзы Микаэляна, как след ует из ур. (29) и (35), был увеличен показатель преломления на оси n0 = 3,47 (кремний,

Si). Другие параметры моделирования тоже изменились (рис. 5а): длина волны λ = 1 мкм, ширина линзы 2R = 6 мкм, длина линзы 2L = 4,92 мкм.

0,0 ____________^

• б)    -3                  0                  +3

Рис. 5. Мгновенная картина амплитуды электрического поля ТЕ-поляризованной световой волны в линзе Микаэляна с точечным источником на передней плоскости линзы (а) и усредненное распределение интенсивности в задней плоскости линзы (б) (по оси ординат отложены произвольные единицы)

Шаг моделирования по пространственным осям во всех примерах равен λ/100. Ширина гауссового точечного источника света в начальной плоскости равна λ/20. На рис. 5а показана мгновенная картина амплитуды электрического вектора световой волны в линзе Мик аэляна, рассчитанной в момент времени , когда световая волна от источника прошла 200 мкм. На рис. 5б показано распределение усредненной интенсивности света ТЕ-поляризованной волны на выходе из линзы (рис. 5а), на «задней» плоскости линзы Микаэляна. Расчет показал, что для интенсивности, показанной на рис. 5б, ширина центрального максимума по полуспад у в изображении точечного источника равна FWHM = 0,12λ. Однако интенсивность (или плотность мощности света) не является той величиной, которая показывает, какая часть мощности излучения источника распространяется в пространстве вдоль оси z. Поэтому на рис. 6 как раз показана такая величина: проекция на оптическую ось вектора Умова-Пойнтинга, рассчитанного на выходе из линзы Микаэляна (рис. 5а), на входе которой был расположен точечный источник света.

Рис. 6. Распределение вдоль оси x величины проекции на ось z вектора Умова-Пойнтинга (в относительных единицах), рассчитанного на выходе линзы Микаэляна (рис. 5а) с входным точечным источником

Ширина центрального максимума потока мощности вдоль оси z на рис. 6 такая же, как и на рис. 5б и равна FWHM = 0,12λ.

Величина дифракционного предела, которого можно достичь при фокусировке света в однородной среде, известна и равна 0,5λ/n, где n – показатель преломления однородной среды. Для наш его случая n0 = 3,47, поэтому дифракционный предел равен FWHM = 0,144λ. Таким образом, из рис. 5б и рис. 6 след ует, что с помощью микролинзы Микаэ ляна (рис. 5а) можно преодолеть дифракционный предел не только в свободном пространстве, но и в среде. Причина этого, на наш взгляд, заключается в том, что при фокусировке света на границе раздела двух сред в формирование фокуса дают вклад и поверхностные неоднородные волны, которые могут формировать интерференционные и дифракционные картины с периодом много меньшим длины волны [9, 10]. То, что поверхностные волны присутствуют при формировании изображения точечного источника, видно из рис. 6. Проекция вектора Умова-Пойнтинга на ось z в некоторой области на оси x отрицательна, то есть вблизи выходной поверхности линзы Мик аэляна свет не только выходит из линзы, но и заходит в нее, то есть вдоль поверхности микролинзы распространяется поверхностная волна. При распространении света в свободном пространстве при удалении от поверхности линзы ширина изображения точечного источника быстро увеличивается, и на расстоянии от поверхности, примерно равным длин е волны, ширина изображения достигает дифракционного предела 0,5λ.

Заметим, что смена знаков проекции вектора Умова-Пойнтинга, аналогичная рис. 6, ранее наблюдалась в работе [8], была названа оптическим вихрем и интерпретирована как интерференция распространяющейся волны и усиленной поверхностной волны. Однако в [8] рассматривалась 1D многослойная структура (1D фотонный кристалл).

На рис. 7а показана мгновенная картина амплитуды электрического вектора световой волны в линзе Микаэ ляна (параметры такие же, как для рис. 5а), когда перед ее входной (нижней на рис. 7а) поверх- ностью на расстоянии 10 нм находятся два точечных источника (шириной по 50 нм), разделенных расстоянием 300 нм. На рис. 7б показано усредненное распределение проекции на оптическую ось вектора Умова-Пойнтинга, рассчитанное за выходной поверхностью микролинзы на расстоянии 10 нм.

• б)     -з                  о                  +з

• 4 .2. Сверхразрешение с помощью микролинзы «рыбий глаз»

Рис. 7. Мгновенная картина амплитуды электрического вектора световой волны с ТЕ-поляризацией в линзе Микаэляна (рис. 5а), когда перед ее входной (нижняя горизонтальная линия на рисунке) поверхностью на расстоянии 10 нм находятся два точечных источника (шириной по 50 нм), разделенных расстоянием 300 нм (а); усредненное по времени распределение проекции вектора Умова-Поинтинга на оптическую ось, рассчитанное на расстоянии 10 нм от задней (верхняя горизонтальная линия на рисунке) плоскости линзы (по оси ординат отложены произвольные единицы) (б)

Из рис. 7б видно, что два источника разрешаются, при этом величина сверхразрешения равна 0,3λ, что меньше, чем в работах [2,4,5,11].

Наряду с рассмотренной в предыдущем разделе микролинзой Мик аэляна можно использовать и другие градиентные изображающие оптические элементы, зависимость показателя преломления от координат которых получена в явном аналитическом виде.

Одним из таких оптических элементов является «рыбий глаз» Максвелла [18,26,27], функция показателя преломления которого в двумерном случае в полярных координатах имеет вид:

n (r ) = n 0

1+

-1

где n0 – показатель преломления в центре круга, R – радиус элемента. Из (38) видно, что при r = R показатель преломления уменьшается в 2 раза. Недостатком этого элемента является ограниченный перепад показателя преломления в центре и на краю оптического элемента: он не может изменяться больше, чем в 2 раза. В линзе Микаэляна перепад показателя преломления определяется только материалом. Например, для кремния показатель меняется от 3,47 до 1. Однако «рыбий глаз» обладает круговой симметрией, и поэтому любой точечный источник, расположенный на его поверхности, изображается «идеально» в диаметрально противоположенной точке на его поверхности.

На рис. 8а показано мгновенное распределение амплитуды электрического поля ТЕ-поляризованной световой волны внутри 2D микролинзы «рыбий глаз», на поверхности которой находятся два точечных близких источника света.

Рис. 8. 2D микролинза «рыбий глаз» в окне программы FullWAVE и мгновенная картина амплитуды электрического поля ТЕ-поляризованной волны внутри линзы, у которой на входе два точечных источника (свет распространяется снизу вверх) (а), а также распределение усредненной интенсивности в плоскости изображения линзы (по оси ординат отложены произвольные единицы) (б)

Параметры моделирования: показатель преломления в центре линзы n0 = 3,47, радиус линзы R = 2,5 мкм, длина волны света λ = 1 мкм, ширина точечных источников по 0,05λ, и они разделены расстоянием 440 нм или 0,44λ. На рис. 8б показано распределение усредненной по времени интенсивности в плоскости изображения (верхняя горизонтальная линия на рис. 8а). Видно, что два источника разрешаются (разрешение равно 0,44λ по критерию Рэлея 20%). Таким образом, данная микролинза незначительно (0,44λ) преодолевает дифракционный предел в разрешении (0,5λ).

При изображении отдельного точечного источника с помощью данной микролинзы (рис. 8а) получается распределение интенсивности, показанное на рис. 9. Ширина центрального максимума интенсивности по полуспаду равна FWHM = 0,3λ. Из сравнения рис. 9 и рис. 5б можно заключить, что микролинза «рыбий глаз» формирует более широкое изображение (примерно в 2 раза шире) точечного источника, чем микролинза Микаэляна при сравнимых параметрах. Хотя при этом величины разрешения 0,44λ (рис. 8б) и 0,3 λ (рис. 9) сравнимы с величинами сверхразрешения, полученными в [2, 4, 5, 8, 11, 12].

Рис. 9. Усредненное по времени распределение интенсивности электрического поля в плоскости изображения микролинзы «рыбий глаз» (рис. 8а), у которой на поверхности расположен только один точечный источник света (по оси ординат отложены произвольные единицы)

Заключение

В работе получены след ующие результаты:

• -    найдены модовые решения уравнения Гельмгольца для произвольного градиентного планарного волновода; амплитуда моды представлена как экспонента с показателем в виде ряда Тейлора, коэффициенты которого находятся из рекуррентных соотношений (уравнения (9), (10) и (13));

• -    показано, что минимальная ширина моды в квадратичном и секонсном градиентных планарных волноводах равна 0,4 от длины волны в вакууме, деленной на значение показат еля преломления вдоль оси волновода (уравнения (29) и (35));

• -    с помощью моделирования программой FullWAVE показано, что градиентные микролинзы Микаэляна и «рыбий глаз» Максвелла могут формировать изображения со сверхразрешением (рисунки 7 и 8);

• -    для 2D микролинзы Микаэляна показано, что точечный источник света изображается вблизи задней поверхности линзы в виде светового пятна с шириной

по полуспаду интенсивности 0,12 от длины волны в вакууме; это меньше, чем дифракционный предел для кремния с показателем преломления 3,47, который равен 0,144 от длины волны в вакууме, и меньше, чем получено в работах [8,11,12] (рисунки 5 и 6);

• -    также показано, что микролинза Микаэляна разрешает по полуспаду два близких точечных источника, разделенных расстоянием 0,3λ, это меньше дифракционного предела в свободном пространстве, равного 0,5X, и меньше, чем в работах [2,4,5,11] (рисунок 7).

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF PG08-014-1), гранта Президента РФ поддержки ведущих научны х школ (НШ-3086.2008.9) и гранта РФФИ 08-07-99007.