Градиентный алгоритм расчета ДОЭ с наложенными на фазовую функцию ограничениями и с регуляризацией

ДОЭ - это тонкая фазовая пластинка с микрорельефом, которая при освещении ее лазерным светом формирует с высокой эффективностью в заданной плоскости пространства требуемое распределение интенсивности.

Имеется много методов расчета ДОЭ с полутоновой фазой [1-3]. Однако с точки зрения существующих технологий изготовления ДОЭ важно уметь рассчитывать ДОЭ с фазовой функцией имеющей небольшое число (2-5) уровней квантования.

В данной работе предложен и обоснован итеративный алгоритм расчета ДОЭ, который минимизирует критерий, состоящий из функционала невязки и функционала ограничений с регуляризацией произвольного порядка.

E 0 ( S n ) = E 0 ( Ф п + S n V E 0 )

- линейная функция:

да

- 1

s n = ^E 0⁽ Ф п ^{( x} ))

J ( V E ₀ ) ² dx

Градиентный алгоритм

Для решения задачи расчета ДОЭ необходимо решить нелинейное интегральное уравнение вида

где

-да

да

I ₀( u ) = J A 0 ( x )exp [ i ф ( x ) ] exp [ i2 n xu ] dx ,

-да

да                               да

J ( V E 0 ) ² dx = 4 J 4 ( x )| g n ( x )|² X

-да                       -да

X sin ² [ Ф п ( x ) - arg( g n ( x ))] dx

где A 0 ( x ) - амплитуда света, освещающего ДОЭ; Ф (x ) - искомая фаза ДОЭ; 1 ₀( и ) - требуемое распределение интенсивности, которое должен сформировать ДОЭ в плоскости изображения.

Показано [2], что алгоритм Герчберга-Сэкстона (ГС), широко применяемый для решения уравнения (1), является градиентным методом с неоптимальным выбором шага и минимизирует функционал невязки:

да

E о ( ф ( x )) = J W ( и ) [| G n ( и )| -| F ( и )| ] ² du ,       (2)

-да где W(и) - весовая действительная функция, 1/

( F ( и ) ( = 1 ₀ ^/2 ( и ) - заданная амплитуда в плоскости изображения, а

Gn (и) = 3[ gn (x)] = да

= J A 0 ( x )exp [ i ф _n ( x ) ] exp [ i 2 ~ xu ] dx

-да

Расчет ДОЭ с квантованной фазой

Для решения задачи расчета ДОЭ с квантованной фазой сформируем вспомогательный функционал, который назовем функционалом ограничений B. Для этого воспользуемся результатом, полученным в [4]: если фазу произвольной комплексной функции g(x) = (g(x)(exp [iф(x)] квантовать по N эквидистантным уровням, то фурье-образ полученной функции будет удовлетворять соотношению да

G(и) = X dmGm (и), m=-да

где да

G m ( и ) = J g m ( x )exp [ i 2 n xu ] dx ,

-да gm (x) = g(x)| exp [i (Nm + 1)Ф(x)] ,

- текущее приближение к ней на n-й итерации, 3 - обозначение Фурье-преобразования.

Процессу сходимости алгоритма ГС присущ эффект стагнации, поэтому целесообразно использовать один из градиентных методов с точным вычислением градиентного шага. В градиентном методе минимизации функционала (2) реализуется итеративный процесс вида

Ф п + 1⁽ x ) = Ф п ⁽ x ) - S n ^V E 0 ,                          ⁽⁴⁾

d m = sin c [ m + (1/ N )],

. , , sin n x sin c ( x ) =-------.

n x

Исходя из этого функционал ограничений запишем в виде

да

B =J

-да

M

G ( и ) - X d m G m ( и )

m =- M

du ,

где ern(x) - приближение искомой фазовой функции на n-й итерации, VЕо = ^0— градиент функцио-дФп (x)

нала (2) на n-й итерации, S_n - длина шага.

В [2] показано, что для функционала (2) имеет место следующее выражение для градиента:

где M - конечное число членов ряда (9).

Тогда решение задачи расчета градационного ДОЭ сводится к минимизации общего функционала

E = E ₀ + P B

где в >  0 - действительное число.

Градиент функционала по фазовой функции Ф (x) имеет вид:

где gn (x)   3 [ Gn (и)],

5 B

5ф ( x )

G n ( и ) =

= W ( и )[ G ( и ) -| F ( и )| G n ( и ) G n ( и )| - 1 ]

= 2Re Н G ( и ) - X d m G m ( и )

да

-да

да

m =-да

X

В [2] была определена длина шага S n при допущении, что

X

d G ( и ) _     d d G m ( и )

дФ   m ^X m дФ

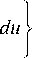
= И я ⁽ x )|^{2 -}

M

- i E dm [(Nm + 1)8*(x)8 m (x) + m =-M

+ 8 m ( x ) 8 ⁽ x ^)] +

MM

+ i E dm8*m( x) E dn (Nn + 1) 8n (x) = m=-Mn

M2

= -2 E dmNm (8(x)( sin(Nmф(x)) - m=-M

MM

• - 2 E dm E dn (Nn + 1)18(x)|2 x

• 3. Регуляризация задачи расчета ДОЭ

m=-Mn x sin( N (m - n )ф (x))

Запишем регуляризирующий функционал r-й степени [5]:

Q_r = J p_r ( u ) ( G ( u ) ( ² du ,                      (12)

-да r где pr (u) = E clu2l , cl > 0 - действительные кон-l=0

станты.

Вычислим градиент функционала регуляризации dQr =

Эф ( x )

= 2Re J [ p_r ( u ) G * ( u ) ^d Gu du ^J = ,         (13)

Ц           дф ( x )    J

= 21ml 8 ^{( x} ) 8 P ^{( x )]} где

8 p ^{( x} ) = 3^{- 1} [ G p ⁽ и ) ] ,

G p ^{( u} ) = P_r ^{( u} ) G ^{( u} ).

Тогда решение задачи расчета ДОЭ с регуляризацией сводится к минимизации общего функционала

E = Eо + aQr где а > 0 - действительное число.

Численные результаты

В численном эксперименте проводилось сравнение стандартного и регуляризированного [6] алгоритмов ГС со стандартным градиентным (СГ) и регуляризированным градиентным (РГ) методами.

Стандартный алгоритм ГС состоит из следующих шагов:

• а)    выбирается начальная оценка фазы ед 0 (x) ;

• б)    выполняется преобразование (3), и полученная функция G 0 (u) заменяется на функцию G ‘ ( u )

G n ( u ) = | F ( u )| G n ( u ) G n ( u )|

• в)    выполняется обратное к (3) преобразование, и рассчитанная функция 8 ‘ ( x ) в плоскости ДОЭ заменяется на 8_n ( x )

₈ ( _x ) = J A o ^{( x} ) 8 n ^{( x} )| 8 n ^{( x} )|"’, ^x е D ,          (15)

[ 0, x t D, где D - форма апертуры ДОЭ. После пункта (в) переходят к пункту (б) и так далее.

В регуляризированном алгоритме ГС согласно [6] вместо замены (14) используется замена

G n ^{( u} ) = ( ^{F ( u} ) ( G n ^{( u} ) ^[( G n ^{( u} ) ( + ^а p_r ^{( u} ) ] ^{1        (16)}

где а > 0 - стабилизирующая постоянная.

В численном эксперименте рассчитывался ДОЭ с фазовой функцией 64х64 отсчетов фокусирующий излучение в равномерный прямоугольник 32х16 отсчетов.

На рис.1 представлены центральные сечения распределения интенсивности в плоскости наблюдения:

• а)    для стандартного ГС (отклонение рассчитанного распределения интенсивности от заданного в плоскости наблюдения -15.1%, эффективность - 96.4%,

• б)    для регуляризированного ГС (13.4%, 92.3%),

• в)    для СГ метода (7.5%, 84.2%),

• г)    для РГ метода (6.2%, 83.4%).

  
  
  
  

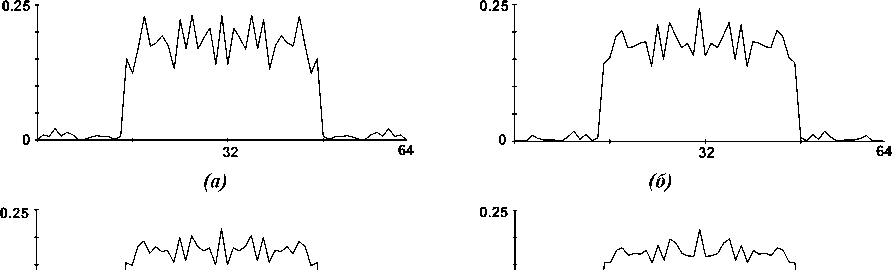
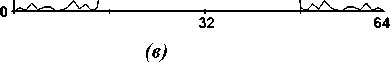
  Рис. 1. Сечения интенсивности света прямоугольника с постоянной интенсивности, рассчитанная различными методами: а) ГС методом, б) регуляризированным ГС методом, в) СГ методом, г) РГ методом.

  
  
  
  
  
  

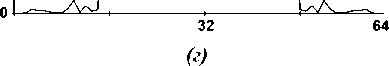
  (а)

  
  
  

  (б)

  
  

Рис. 2. Двумерное изображение распределения интенсивности в фокальной плоскости, рассчитанное РГ методом за 40 итераций (а) и фазовая функция ДОЭ (б) формирующего данное распределение интенсив- ности.

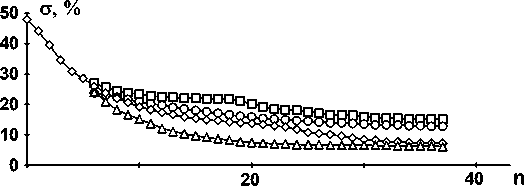
стандартный алгоритм ГС регуляризированный алгоритм ГС стандартный алгоритм ГМ регуляризированный алгоритм ГМ

Рис. 3. Зависимость среднеквадратичного отклонения рассчитанной интенсивности в фокальной плоскости от заданного постоянного значения от числа итераций.

На рис.2 изображена рассчитанное регуля-ризированным ГМ распределение интенсивности в плоскости наблюдения (а) и фазовая функция (б).

На рис.3 показаны зависимости среднеквадратичной ошибки рассчитанной интенсивности от числа итераций для различных алгоритмов расчета.