Градиентный метод оптимизации в задаче синтеза бинарной микрооптики

Когда минимальный характерный размер дифракционных структур приближается к длине волны освещения, необходимо применять векторную модель для анализа дифракции от них. Также векторная модель требуется, когда представляющая интерес область находится вблизи дифракционного элемента и, тем более, внутри него. Аналитические векторные модели дифракции могут быть определены для некоторых периодических структур, для апериодических структур граничные условия на электромагнитные поля делают аналитическую модель невозможной. Следовательно, для моделирования дифракции от апериодических дифракционных оптических элементов (ДОЭ) должны использоваться численные технологии, основанные на решении уравнений Максвелла. В работах [1], [2] и [3] описаны подходы к решению задач ближнего поля в свободном пространстве и в волноводе соответственно. Показано, что при использовании рефракционных микролинз наблюдается смещение максимума интенсивности от геометрического фокуса. При построении дифракционных микролинз из рефракционных наблюдается сдвиг положения фокуса и снижение эффективности дифракционной микролинзы [4]. Невозможно использование рефракционных микролинз в задачах с фокусировкой вне оптической оси вследствие их симметричности. В связи с этим возникает необходимость применения оптимизационных методов для синтеза дифракционных оптических элементов, способных определить оптимальный профиль для заданного распределения интенсивности, принимая во внимание ограничения на форму рельефа. В данной статье мы представляем градиентный алгоритм для синтеза бинарной микрооптики.

Метод расчета

Используя гибридный метод конечных элементов - граничных элементов [1], рассмотрим дифракцию света в свободном пространстве.

Для неоднородной диэлектрической двумерной среды для двух случаев поляризации можно записать уравнение Гельмгольца для монохроматической электромагнитной волны:

^д 1 ^д ^ ⁽ х , у ) дх а дх

^д 1 ^д У ^{( х} , У ) ду а ду

+ k 0 ву ( х , у ) = 0,

, и , где для ТЕ-поляризации у = Е а = Uo

Q £(х, у) , I------ to   2п в = ^^, k о = to>0 £ о = - = у ео                     с А)

вол

новое число в вакууме, Х ₀ - длина волны падающего света, ш - циклическая частота излучения; £ , е ₀, ц , ц ₀ - диэлектрические и магнитные проницаемости вакуума и среды;

rr

Е, Н - вектора электрической и магнитной напряженности электрического и магнитного полей; для ТМ-поляризации: у = H z, а = ^(^1^2, в = А £о          Ао '

Решение уравнения (1) равносильно минимизации функционала, рассчитываемого в ограниченной области Q, включающей свою границу S [1]:

ней нормали на границе S.

Элементы матрицы А вычисляются по формулам:

(

a k,j = JJ

^В к , j

d ю ^Bk’ j (X, у ) ^do j '^{J (} X у ) +

А к V

3x

3x

F ^{¥ 2} = Л /¹ a ^V V ⁽ X’ У ^{) V} V ⁽ X’ У ^{2 -} Q L А X, У )

- к о² £ ( X, у) ¥ ² (X, у )\ыу - 2 J ^VdU- S d n

Приведем уравнение (2) к системе линейных алгебраических уравнений, используя следующую расчетную схему. Покроем область Q треугольной сеткой. После этого в каждом из треугольников построим линейный полином. Для однозначного определе ния полиномов достаточно задать их значения в вершинах треугольников. Тогда базисом будет система функций wk(X, у). Геометрически функция wk(X, у) представляется как треугольная пирамида с центром в точке (Xk, у)

Представим поле у через данный базис как

+ d ю ^{Q k}'^J (X, у ) ^d^^k ’ ^{j (} x у ) d y          d y

^{- k} о² £ к ^{ю Q} k ’' ( X’ у ^ ю ^ ’ j

( X , у )

dcdy ,

,

k, j = 1, ..., N + M, где Q k j. - треугольная область, содержащая к и j узлы сетки.

Элементы матрицы В вычисляются по формулам:

Sm’ ptoSm’ p b = - J юm юp di,        (7)

m-p     Sm, p m, p = 1, ..., M.

Получаем систему линейных уравнений, которую необходимо дополнить соотношением для поля и его производных на границе [6]:

N

V ( x, у) = ^ V к ^ю к ⁽ X’ У),      (3)

к = 1

S i

d v ^sc

G 2 - V^SC d n

^d G 2 d n

1 „

W = - -v sc ,(X’ у ) е S,(8) 2

где к = 1, ..., N + M; N - число внутренних узлов сетки, M - число граничных узлов, приходим к системе линейных алгебраических уравнений:

Подставляя разложение (3) в функционал (2) и применяя разделение общего поля на сумму падающего и рассеянного полей, приравниваем нулю производные dFVl = о, (x, у) е Q (4) dV kc и приходим к системе линейных алгебраических уравнений [5]:

A (y □ + У В ) + B ( v sc + v in ) = 0,    (5)

где у _в = ( V 1 , ., ¥ N ); V к = V к + V kn , V , V inn - полное, неизвестное рассеянное и известное падающее световые поля; v = (v_p .,

¥ v M ^); v ^k    d n

- производная поля по внеш

где функция Грина для двумерных световых полей (цилиндрическая волна) равна функции Ханкеля второго рода нулевого порядка:

G ⁽ x X ’ у, у ' ) = ^- 4 H о²⁾ ( ^к о _хи ^X ' )² + (у ^- .Д)² j .(9)

Равенство (8) может быть представлено в матричном виде:

[ C ] 0 S^c +[ D ] v Sc = о, (1о) где элементы матриц [ C ] и [ D ]:

Cm.p = - h 1о1юР> (РР + [ РР+1 - РР ]^ )Х dG(Рm ’ Рp + [Рp+1 - Рp ]^) ,,

Х

- hJ0ю Sp Р£-1 + [ Рp - Рр-1]^)х(11)

^{d G(} Р m ’ Р p-1 ^{+ [} Р p ^- Р p-11 ^ )

х-------p---—p---p dn'

+ y 5

1 / mvmp ’ dm,p = h/0®р pp + [ Рp+1 - Рp ]i)x x G(Рm , Рp + [ Рp+1 - Рp ]i М +

⁺ Ч /® Р ( Р p-1 ^{+ [} Р p - Р Р-1 ^] ^ ^{)Х    (12)}

^{x G(} Р m , Р p-1 ^{+ [} Р p ^- Р ^К Ж

После нахождения поля y ^sc на границе S поле в любой точке окружающего пространства находится по формуле:

. I ду ^sc            d G^

У ( x , y ) = у  ( x , y ) - / ^ -. G _; - у ²

р I d n             d n

( x , y ) й Q

чП,

m,p = 1, ..., M, где n' - вектор внутренней нормали; p m = (x m , y m ) _E S - координаты m -ой точки; h - шаг сетки; параметр у^ O_m/(2n). где ф_m - внутренний угол в точке (x m , y m ) границы S.

После линеаризации уравнения (8) получаем полную систему линейных алгебраических уравнений вида:

^[ A G,G ^{] [} A S ,G ^]

^[ A G , S ^{] [} A S , S ^]

_     0       [ C ]

[ A G ,G ^{] [} A S , G ^]

= _ ^[ A G ,S ^{] [} A S , S ^]

0     0

В матричном виде поле в окружающем пространстве представляется в виде:

y = y ⁱⁿ + W y ^sc = y ⁱⁿ + WT ^-1 U y ⁱⁿ . (17)

0 1

, sc

⁰ G

^{[ B ]} 0 [ d ] J v

sc

S sc

in

0 G

^{[ B ]} 0

v

in

S in

,

где G - область Q без границы S, подматрица A G _g размерностью NxN включает коэффициенты вклада внутренних узлов, подматрицы A _gs и A _sg размерностью NxM и MxN включают коэффициенты вклада внутренних узлов с внешними, подматрица A _SS размерностью MxM включает коэффициенты вклада внешних узлов, y _G и У _S - вектора значений поля во внутренних и граничных узлах сетки.

Представим систему уравнений (13) в

матричном виде:

T ysc = U yin ysc = T-1U y in где

T =

U

^[ A g , g ^]

^[ A g , s ^]

^[ A s , g ^{] [} A s , s ^] [ C ]

[B]

И

, 0

sc

0G sc

0 S

vsc

где матрица W размером 1x(N + 2M) равна:

W = [0 [E] [f]], где элементы подматриц E и F:

ep (x, y) = h/0®р (P p + [ Р p+1 - Р p ]^ )x dGP x, y), Р p + [ Р p+1 - Р p]i ) x--------p---p----p— di + dn'

^{+ h} i 0 ® ^{р (} Р p - 1 ^{+ [} Р p ^- Р p - 1^{] i )x}      (18)

dGPx, y), Рp-1 +[Рp - Рp-1]i) x-----------p---;—p----p----di, dn'

^[ A g , g ^{] [} A g , s ^]

^[ A s , g ^{] [} A s , s ^]

in

0G in

0S in

fp (x, y) = - h/0 toSp (Рp + [Рp+1 - Рp ]i )x x G(( x, y), р p +[ р p+1 - р p ]i )di -

^{- h} / 0 ® ^S ( p p - 1 ^{+ [} р p ^- р p - 1^{] i )x    (19)}

xG((x,y),рp-1 +[рp- рp-ji)di, p = 1, ..., M.

Метод оптимизации

Определение оптимального профиля состоит в расчете параметров (y 1 , ..., y k ) профиля бинарной микрооптики (рис.1). Это достигается разработкой алгоритма систематического поиска оптимального решения. В качестве метода оптимизации мы выбрали градиентный метод.

Для построения процедуры расчета введем функцию ошибки е ( p ), характеризующую отличие рассчитанных значений интенсивности I от требуемых значений I ’ [7]:

е (Р) = е (I(p), I’), где p = (y1, ., yk) - вектор параметров бинарного профиля; k - число параметров профи-

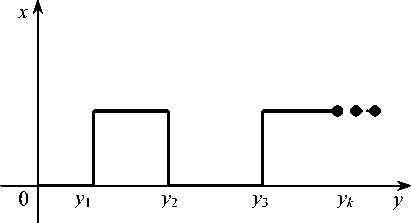
Рис. 1. Бинарный профиль микрооптики

ные матрицы; у ( р ) - комплексный вектор. Из(15)следует:

d 0 sc ( р ) _ T — 1 д и ( р )

dPi отсюда:

д Т ^— ‘ ( р ) _Г Э ф sc ( р )

dPi

, in , ^{д Т    ( р )} _Тт, in

0 +   ----U0  , dPi

dPi

ля; ( I n ) M_M , ( I ’) MM - вектора рассчитанных и требуемых значений интенсивности.

Градиентная процедура минимизации функции ошибки £ ( р ) состоит в итерационной коррекции параметров профиля микрооптики по правилу:

р , = р — t- V £ (р ), г п+1 n п ’ Пгп/^

где n - номер итерации, t - шаг градиентного алгоритма,

i L ^d P i

Из(14)следует:

гр — 1 ^ди(р) . in /тт . in т — 1

^т IpT ^{0  (U0} ’ ^|2"

д (^Т( р ) 0 sc ( р )) _ T д 0 ^sc ( р ) + д ^т( р )

^dP i

отсюда d0sc (р) _ T dPi

V £ ⁽ р ) =

^<д £ ( р )     д £ ( р ) '

( д у 1

,...,

д У к J

градиент функции ошибки.

Точно определить шаг t не представляется возможным, т.к. неизвестно значение минимума функции ошибки £ ( р ). Поэтому после вычисления градиента функции ошибки V £ ( р ) из исходной точки р _п делается шаг заданной длины, находятся координаты новой точки р _{п +1}. Если значение £ ( р „ ₊₁) лучше, чем £ (р _п ), то шаг считается удачным, и новая точка становится исходной, иначе - шаг неудачный, и его величина уменьшается. Если величина шага становится меньше определенного предела, то алгоритм останавливается, и последняя найденная точка - решение, иначе процедура уменьшения шага повторяется.

Вычисление градиента функции ошибки V £ ( р ) может вестись двумя способами. Первый заключается в непосредственном ^{д £ (} р ) нахождении частных производных » _х, в разностном виде.

Второй способ состоит в представлении £ ( р ) через вектор электрического поля у ( р ), учитывая зависимость I = У У *.

Электрическое поле у определяется из системы (17), где Т ( р ), и ( р ), W - комплекс-

^dPi      ^dP i

_ д и ( р ) ₀ in ^dP i       ’

1 ^{д и}( р ) 0. L dP,

д Т ( р ) ^dPi

sc ₀ sc

Подставляя (21) в (20), получим:

д Т ^— ‘ ( р ) _ ^d P i

. (21)

Т ^{— 1} 1^ ^Ф" ( U0” ) " ' • (22)

Найдем выражение для производной поля в любой точке окружающего пространства по параметру р из системы (17), используя (22):

д 0 ( р )_ д ( WT ^{- 1}( p ) U ( p ))

^dP i

dPi

0 in in

_ wT^

= WT

' —

dPi

( р ) U + T — 1 д ^и( р )

■ 1    д Т ( р )

^“ ---------

dPi

Ф 5С ,

+

dPi

• in

d U ( p ) ₀ in

dPi

•

Учитывая (13) можно записать:

д 0 ( р ) _ ^dPi

= WT

I—I

= WT

-1 Fd A i , i ( р )

—

L    ^dPi

. 1 d A i , i ( р ) ^dPi

in ^ø

d A i , i ( p )

^d P i

I sc ^ø

( 0 ⁱⁿ — 0 ^sc )

_{о о}                        о д £ ( р )

Элементы вектора градиента — ^dPi

Pi - компонента вектора р , имеют вид:

, где

d £ ( p ) = у d £ ( I , I ') ^d I j ( Р )

dPi j dIj     dPi ’ dIj (Р)   , d0j(P)     * d0 j (Р)

= ⁰ j + ⁰     -p.   • ⁽²⁵⁾

Для определения V £ ( p ) уравнение (24) подставляется в уравнение (25).

Отметим, что данный подход позволяет определять любые другие параметры, подлежащие оптимизации.

Проведен ряд экспериментов, показывающий эффективность использования градиентного метода оптимизации бинарных микролинз.

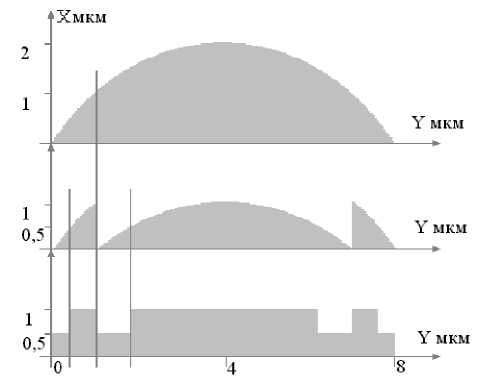
Рис. 3. Построение линзы с фазовой функцией, приведенной по модулю 2П, и бинарной дифракционной линзы

Конструкция дифракционной линзы

Рассмотрим цилиндрическую рефракционную микролинзу (рис.2).

Положим, что ее длина L x настолько больше ширины L y , что длину линзы по сравнению с шириной можно считать бесконечной. Рассмотрим численный пример. Определим апертуру линзы как а = 8 мкм, радиус кривизны R = 5 мкм, показатель преломления n = 2 для длины волны Х₀ = 1 мкм, что примерно соответствует хлориду серебра (n_AgCl = 2,02239 для Х₀= 1 мкм).

Для данной цилиндрической линзы построим линзу с фазовой функцией, приведенной по модулю 2п, и дифракционную линзу с двумя степенями градации фазовой функции (рис.3).

Численное моделирование и оптимизация

Поставим вычислительный эксперимент, в котором плоская волна TE-поляризации падает на бинарные линзы в свободном пространстве. В качестве оптимизируемых параметров профиля брались координаты выступов.

На рис.4 показано распределение интенсивности дифракции плоской волны на построенной однофокусной бинарной линзе (рис.3) с дифракционной эффективностью 54,3 % и энергетической эффективностью 43,5 %. Ее профиль был использован в качестве начального для процедуры оптимизации и был оптимизирован до дифракционной эффективности 72,3 % и энергетической эффективности 64,0 %.

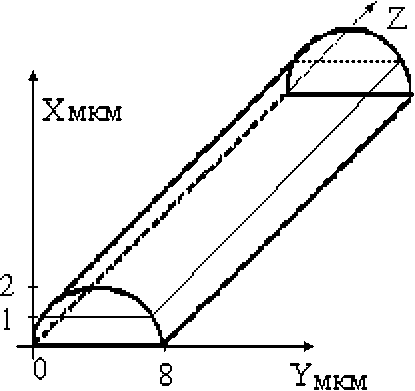
Рис. 2. Цилиндрическая рефракционная микролинза

Рис. 4. Распределение интенсивности света при дифракции на бинарной линзе начального

построения

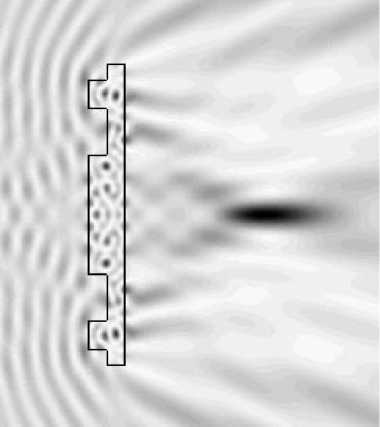
Рис. 5. Распределение интенсивности света при дифракции на оптимизированной бинарной линзе

Под энергетической эффективностью мы понимаем отношение энергии, попавшей в область фокуса, к энергии, падающей на микролинзу. Дифракционная эффективность - это отношение энергии, попавшей в область фокуса, к энергии, прошедшей микролинзу. Интенсивность - это квадрат модуля проекции электрического вектора на ось z.

Рассмотрим синтез бинарной линзы, дающей в плоскости, располагающейся на расстоянии 3,5 мкм, три максимума равной интенсивности шириной 1 мкм: один в центре и два на расстоянии 2,5 мкм от центра. Были использованы несколько начальных профилей линзы с тремя выступами, располагающимися симметрично относительно

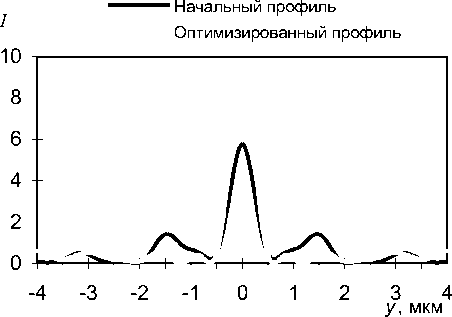
Рис. 6. Распределение интенсивности света в фокальной плоскости бинарных линз: с начальным профилем и оптимизированным оси симметрии, для нахождения по возможности всех локальных экстремумов функции ошибки. В результате работы процедуры оптимизации было найдено два вида профиля, дающих максимальные значения эффективности. На рис.7 показано распределение интенсивности дифракции плоской волны на оптимизированных трехфокусных бинарных линзах. Линза, показанная на рис.7а, дает дифракционную эффективность 86,2 % и энергетическую эффективность 79,3 %. Линза, показанная на рис.7б, дает дифракционную эффективность 85,8 % и энергетическую эффективность 84,1 %. Дифракционная эффективность в этом случае равна отношению энергии в трех заданных порядках к энергии, прошедшей микролинзу. Под энергией понимается сумма интенсивностей на выбранной линии вдоль оси у.

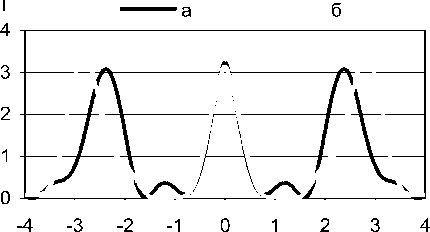
б)

а)

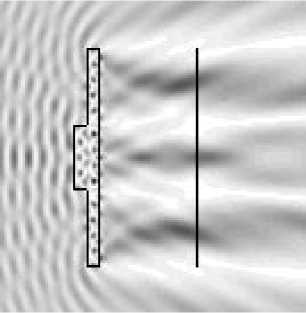
Рис. 7. Распределение интенсивности света при дифракции на оптимизированных трехфокусных бинарных линзах

z, мкм

Рис. 8. Распределение интенсивности света при дифракции на оптимизированных трехфокусных бинарных линзах в указанной плоскости

Таким образом, представленный алгоритм позволил найти профиль трехфокусной бинарной линзы (рис.7б) с высокой дифракционной эффективностью и глобальным максимумом энергетической эффективности, более простой в физической реализации, чем линзы с начальным профилем. Линза, показанная на рис.7а, с глобальным максимумом дифракционной эффективности дает форму поля дифракции наиболее соответствующую заданной.

Выводы

В работе рассмотрен градиентный метод расчета профиля диэлектрического микрообъекта с использованием совместного метода конечных - граничных элементов. Работоспособность метода продемонстрирована на примере расчета бинарных однофокусной и трехфокусной микролинз.