Градиентный метод расчета каскадных ДОЭ для фокусировки излучения различных длин волн

Фазовые дифракционные оптические элементы (ДОЭ) применяются при решении большого числа различных задач по преобразованию и фокусировке лазерного излучения [1–4]. Конструктивно фазовые ДОЭ выполняются в виде дифракционного микрорельефа на пропускающей или отражающей подложке, который осуществляет фазовую модуляцию падающего излучения. Расчет ДОЭ является обратной задачей, состоящей в определении такой функции высоты дифракционного микрорельефа (или пропорциональной высоте функции фазовой модуляции), которая в рамках скалярной теории дифракции обеспечивает формирование светового поля с заданными характеристиками (как правило, с требуемым распределением интенсивности в некоторой плоскости). Для расчета ДОЭ были предложены различные итерационные алгоритмы, в частности, алгоритм Гершберга– Сакстона и ряд его модификаций [5– 10].

Важно отметить, что в сложных задачах, включающих, например, формирование нескольких различных распределений интенсивности для нескольких различных падающих пучков (в т.ч. с различными длинами волн), одиночные ДОЭ имеют относительно невысокие рабочие характеристики. Для решения таких задач применяются т.н. каскадные ДОЭ, которые состоят из нескольких последовательно расположен- ных ДОЭ и обладают значительно более широкими функциональными возможностями [2, 11 – 14]. В частности, помимо решения задач формирования различных распределений интенсивности для различных падающих пучков каскадные ДОЭ нашли широкое применение при решении различных задач машинного обучения [14–20], а также в задачах реализации различных математических преобразований, описываемых линейными операторами [21 – 23]. В этих задачах, в силу наличия ряда аналогий между каскадом ДОЭ и нейронными сетями, каскадные ДОЭ стали называть дифракционными нейронными сетями (ДНС) [15]. Основным методом расчета ДНС является стохастический градиентный метод, а также основанные на нем «улучшенные» методы 1-го порядка [24].

Большой научный и практический интерес представляет задача расчета каскадных ДОЭ, предназначенных для работы с излучением различных длин волн [2, 22, 23, 25–28]. Далее будем называть такие каскадные ДОЭ (или ДНС) спектральными каскадными ДОЭ (или спектральными ДНС). В частности, в недавних работах [22, 23] были рассмотрены спектральные ДНС для оптической реализации различных линейных преобразований на различных длинах волн (каждое преобразование осуществляется на своей длине волны), а также для формирования мульти-спектральных изображений. Расчет спектральных ДНС в [22, 23] был основан на стохастическом гради- ентном методе, который показал хорошие рабочие характеристики. В то же время градиентные методы для задачи расчета спектральных ДОЭ, формирующих несколько различных распределений интенсивности для падающих пучков с несколькими различными длинами волн, остаются недостаточно проработанными. Для краткости назовем эту задачу задачей фокусировки различных длин волн (ФРДВ). Расчет одиночных и каскадных спектральных ДОЭ для решения задачи ФРДВ был рассмотрен в работах [2, 11, 12, 24–27]. В указанных работах для расчета спектральных ДОЭ были использованы итерационные алгоритмы, являющиеся обобщением алгоритмов, предложенных для расчета «обычных» ДОЭ, работающих с излучением одной длины волны. Данные алгоритмы являются эвристическими и не имеют строгого теоретического обоснования. По мнению авторов настоящей статьи, наиболее значимые результаты в задаче ФРДВ были получены в работе [2]. В данной статье был предложен итерационный метод для расчета спектральных каскадных ДОЭ и рассчитаны каскадные ДОЭ для формирования различных изображений букв на различных длинах волн. В то же время предложенный в [2] итерационный метод расчета также является эвристическим. В частности, данный метод не обладает свойством неувеличения ошибки, которым обладают алгоритм Гершберга–Сакстона и алгоритм уменьшения ошибки. Таким образом, разработка и исследование градиентного метода для расчета спектральных ДОЭ для задачи ФРДВ представляет большой интерес.

Именно такой градиентный метод расчета каскадного спектрального ДОЭ рассмотрен в настоящей работе. В рамках метода задача расчета ДОЭ сформулирована как задача минимизации функционала, зависящего от функций высот дифракционного микрорельефа каскадного ДОЭ и представляющего ошибку формирования заданных распределений интенсивности на расчетных длинах волн. Для производных функционала ошибки по функциям высот дифракционного микрорельефа получены явные и компактные выражения. С использованием предложенного градиентного метода рассчитаны каскадные спектральные ДОЭ для фокусировки излучения для трех различных длин волн в различные области в виде изображений букв. Представленные результаты численного моделирования демонстрируют хорошие рабочие характеристики предложенного метода.

1. Постановка задачи расчета спектрального каскадного ДОЭ

Рассмотрим задачу расчета спектрального каскадного ДОЭ, формирующего заданные распределения

W m , q ( U m ) = C m , q jj W m - 1, q ( U m - 1 ) T m - 1, q ( u m - 1 ) eXP ] i ~

[ ^X q d m

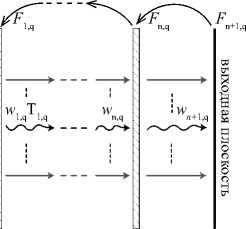
интенсивности для Q различных падающих пучков с различными длинами волн X q , q =1,..., Q . Будем считать, что каскадный ДОЭ состоит из n фазовых ДОЭ, расположенных в плоскостях z = f 1 ,…, z = f n (0< f 1 <…< f n ) и задаваемых функциями высоты дифракционного микрорельефа h 1 ( u 1 ),…, h n ( u n ), где u j = ( u j , v j ) – декартовы координаты в плоскости z = f j (рис. 1).

X

X

q

^X Q

ж w 0,1

w

0,q

; w w 0,Q

входная

плоскость

L f0

Обратное распространение поля

w

1,q

Каскад ДОЭ hn(un)

I ₁ , ... , I _Q

h ₁ ( u ₁ )

f ₁

f _n

f n+1

z

Рис. 1. Геометрия задачи расчета спектрального каскадного ДОЭ

Пусть для каждой длины волны X _q е { X i ,..., X q } во входной плоскости z = f 0 =0 задано входное распределение поля (падающий пучок) с комплексной амплитудой w 0, q ( u 0 ). Здесь и далее нижние индексы у комплексной амплитуды поля обозначают индекс плоскости, в которой она записана, и индекс длины волны. Будем считать, что распространение светового поля в свободном пространстве (между плоскостями расположения ДОЭ) представляется интегралом Френеля–Кирхгофа в рамках скалярной теории дифракции, а прохождение светового поля через ДОЭ описывается через умножение комплексной амплитуды падающего поля на функцию комплексного пропускания (ФКП) ДОЭ. ФКП m -го ДОЭ зависит от длины волны и при длине волны X _q имеет вид

T m , q ( U m ) = eXP { i ф m , q ( u m ) } =

= exp

i T“( ⁿ ( X q ) — 1 ) h m ( u m ) ^X q

где ф _m , _q ( u _m ) - фазовая функция m -го ДОЭ (формируемый ДОЭ фазовый набег) при длине волны X _q , n ( X q ) - показатель преломления материала ДОЭ. При сделанных допущениях распространение входных пучков w 0, q ( u 0 ), q = 1, …, Q из входной плоскости z = 0 через каскадный ДОЭ в выходную плоскость z = f n +1 описывается следующей рекуррентной формулой:

( u m - u m - 1 ) [ d 2 u m - 1 , m = 1,..., П + 1,

где w m , q ( u m ), m = 1, …, n – комплексные амплитуды полей, падающих на m -й ДОЭ с ФКП T m,q ( u m ), C m,q = ( i x q d m )^-1exp{ i2n d m / X q }, d m = f m -f m -i - расстояния между плоскостями. Отметим, что при расчете полей w 1, q ( u 1 ), падающих на 1-й ДОЭ ( m = 1 в формуле (2)), следует положить T 0, _q ( u ₀) = 1.

Рассмотрим теперь обратную задачу расчета каскадного ДОЭ. Эту задачу мы будем понимать как задачу расчета функций высот дифракционного микрорельефа h 1 ( u 1 ),…, h n ( u n ) каскадного ДОЭ, обеспечивающих при заданных входных пучках w 0, q ( u 0 ), q = 1,…, Q формирование в выходной плоскости световых полей с заданными распределениями интенсивности I q ( u n +1 ), q = 1,…, Q . Будем считать, что ошибка формирования требуемого распределения интенсивности I q ( u n +1 ) для входного пучка w 0, q ( u 0 ) с длиной волны X _q представляется следующим функционалом в виде интеграла от квадрата ошибки:

8 q ( h l ,..., h n ) = jj ( I n + 1, q ( u n + 1 ) - I q ( U n ₊ 1 ) ) ² d 2 U n ₊ 1 , (3)

где I n +1 , q ( u n +1 ) = | w n +1 , q ( u n +1 )|² – распределение интенсивности, формируемое в выходной плоскости при функциях h 1 ( u 1 ),…, h n ( u n ). Тогда обратную задачу расчета каскадного ДОЭ, формирующего заданные распределения интенсивности I q ( u n +1 ), q = 1,…, Q для всех падающих пучков w 0, q ( u 0 ), q = 1,…, Q с различными длинами волн, можно рассматривать как задачу минимизации суммы указанных функционалов:

Q

e ( h 1 ,...,h n ) = ^s q ( h 1 ,...,h n ) ^ min.

•

2.    Градиентный метод расчета спектрального каскадного ДОЭ

Для функционала (4) несложно рассчитать производные Фреше 5s ( h i ,..., h_n )/ 5 h_m , что позволяет применить для решения задачи (4) градиентный метод. Действительно, поскольку функционал (4) равен сумме функционалов, то его производные имеют вид

5s ( h 1 ,..., h _n ) 5 h m

e 58 q ( h 1 ,..., h n )

q = 1       5 hm      '

n .

Вычисление производной функционала 5s _q ( h ₁, ., h_n )/ 5 h_m в (5) производится так же, как в задаче расчета каскадного ДОЭ, формирующего заданное распределение интенсивности в случае одного падающего пучка w о, _q ( u ₀) с длиной волны X _q . Подробное описание метода вычисления производной функционала для такой задачи приведено в недавней работе [14] авторов настоящей статьи. Согласно [14], данную производную несложно получить с использованием свойства унитарности оператора распространения света через каскадный ДОЭ в виде

58 q ( h 1 ,..., h n ) _

5 h m                                            (6)

= -2y q Im[Wm,q (Um ) Tm,q (Um )Fm,q (um )], где Yq = (2п / Xq)(n(Xq)-1), Wm,q(um) - комплексная амплитуда поля, падающего на m-й ДОЭ при «прямом» распространении поля w0,q(u0) из плоскости z =0 в плоскость z = fm (расчет wm,q(um) осуществляется по формуле (2)), Tm,q(um) – ФКП m-го ДОЭ при длине волны Xq, заданная формулой (1), а Fm,q(um) - комплексная амплитуда поля, получаемая при обратном распространении т.н. «поля ошибки»

F n + 1, q ( u n + 1 ) = [ I n + 1, q ( u n + 1 ) — I q ( u n + 1 ) ] W n + 1, q ( u n + 1 ) (7)

из выходной плоскости z = f n +1 в плоскость z = f m (обратное распространение поля схематично показано на рис. 1). Отметим, что обратное распространение поля в свободном пространстве также описывается интегралом Френеля–Кирхгофа, в котором расстояние распространения берется со знаком минус, а «обратное прохождение» пучка через ДОЭ описывается умножением комплексной амплитуды пучка на комплексносопряженную ФКП ДОЭ. Таким образом, поле F m , q ( u m ) рассчитывается рекуррентно по следующей формуле:

^Fl - 1, q ( ^u I - 1 ) = ^Cl ’, q IT ^Fl,q ( ^u l ) ^Tl * q ^{( u} l ^)eXP i T^T ( ^u l - 1 [ ^X q d l

- u l ) 2 ^ d ² u l , l = n ,

m + 1,

где при расчете поля F n , q,j ( u n ) ( l = n +1) ( l = n +1) следует положить T_{n +1}( u _{n +1}) = 1. Приведенные выражения (57) для вычисления производных функционала ошибки являются основой для решения обратной задачи (4) градиентным методом или каким-либо улучшенным методом оптимизации 1-го порядка, например ADAM [24]. Отметим, что выражения (5)–(7) получены в случае, когда функционалы ошибок 8 q ( h 1 ,..., h n ) имеют вид (3), соответствующий интегралу от квадрата ошибки при длине волны A q . В случае другого вида подынтегральной функции изменится только вид поля ошибки (7), а остальные выражения останутся справедливыми [14].

Отметим, что функции высот дифракционного микрорельефа h 1 ( u 1 ),…, h n ( u n ) обычно предполагаются заданными в некотором интервале [0, h max ), где h max – максимальная высота дифракционного микрорельефа (значение h max обычно выбирается из требований технологии, используемой для изготовления ДОЭ). Наличие ограничений 0 <  h m ( u 1 ) <  h max , i = 1,…, n, делает задачу расчета каскадного ДОЭ задачей условной оптимизации. Для учета указанных ограничений в итерационный процесс расчета функций высот дифракционного микрорельефа следует ввести оператор проекции на множество функций ограниченной высоты

I 0, h <  0,

Pr ( h ) = j h , h e [0, h max ), (9) [ h max , ^h ^ h max .

В частности, введение оператора (9) в градиентный метод расчета каскадного ДОЭ соответствует методу проекции градиента, в котором расчет следующих приближений функций высот hm (um),m = 1,...,n , на шаге k на основе функций высот hm-1 (um),m = 1,...,n , полученных на предыдущем шаге (k-1), осуществляется по формуле hmm (um ) = Pr I hmm-1 (um )-t ^^ ( Um ) I, m = 1,..., П, (10) I о hm J где t – шаг градиентного метода.

3.    Примеры расчета спектральных каскадных ДОЭ

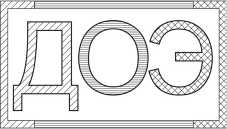
Пусть во входной плоскости каскадного ДОЭ для трех длин волн Z i = 633 нм, X 2 = 532 нм, X ₃ = 457 нм из красной, зеленой и синей частей спектра заданы три входных поля w ₀ , q ( u ₀ ) = A q exp( - u 0 / ст ²), q = 1,2,3, соответствующих гауссовым пучкам с параметром ст =1,2 мм. Рассмотрим расчет каскадного ДОЭ для формирования при указанных длинах волн распределений интенсивности I q ( u n +1 ), q = 1, 2, 3, соответствующих изображениям букв «Д», «О» и «Э» и фрагментам окружающей их рамки (рис. 2). Отметим, что при освещении такого ДОЭ падающим пучком

W = ^ W,q (u0 ) , q состоящим из входных пучков с заданными длинами волн, каскадный ДОЭ будет формировать цветное изображение в виде надписи «ДОЭ» в цветной рамке (рис. 2г).

Далее будем считать, что амплитуды Aq падающих гауссовых пучков w0,q (u0) = Aq exp(-u0 / ст2) выбраны из условия нормировки jj|w0,q (u0 )|2 d2u0 = fjIq (un+1)d2un+1 (11)

обеспечивающего равенство энергий входного пучка с длиной волны X _q и соответствующего ему требуемого распределения интенсивности I q ( u n +1 ).

Расчет функций высоты микрорельефа каскадных ДОЭ, формирующих на расчетных длинах волн распределения интенсивности в виде букв «Д», «О», «Э» в рамке, осуществлялся описанным выше градиентным методом (5)–(10). Отметим, что в данной работе для расчета полей, входящих в выражение (6) для производных функционалов ошибки, использовался метод углового спектра [29, 30].

Были рассчитаны одиночный ДОЭ и каскады из двух и трех ДОЭ. При расчетах предполагалось, что все расстояния между плоскостями dm = fm – fm–1 явля- ются одинаковыми и равны 80 мм. Функции высоты микрорельефа в плоскостях расположения ДОЭ были заданы на сетках 512×512 с шагом 10 мкм. В этом случае размер стороны апертуры каждого ДОЭ составлял 5,12 мм. Поля во входной и выходной плоскостях задавались на сетке 1024×1024 с шагом 10 мкм. Максимальная высота дифракционного микрорельефа предполагалась равной hmax =6 мкм. Отметим, что ДОЭ с такой высотой могут быть изготовлены по стандартной технологии прямой лазерной записи [10, 31]. В качестве показателей преломления материала ДОЭ использовались значения n(X1) = 1,457, n(X2) = 1,461, n(Хз) = 1,465, соответствующие плавленому кварцу.

Д

• (а)           X =633 нм

Э

О

(б)          X =532 нм

(г)

(в)

X =457 нм

Рис. 2. Требуемые распределения интенсивности для трех расчетных длин волн (a)-(в) и результирующее цветное распределение (г), где различные цвета показаны различной штриховкой

Рассчитанные функции высоты микрорельефа одиночного и каскадных ДОЭ показаны на рис. 3. Интересно отметить, что вид областей фокусировки для различных длин волн (см. рис. 2) «проявляется» в структуре микрорельефа в центральных областях рассчитанных ДОЭ. При расчете каждого из примеров было сделано 5000 итераций при экспоненциально убывающем шаге (такое число итераций оказалось достаточным для сходимости метода). В качестве начальных функций высоты микрорельефа использовались реализации случайного процесса белого шума с равномерным распределением значений в диапазоне [0, h max ). Время расчета на видеокарте NVIDIA RTX 3060 12 Gb составило от 4–5 минут для одного ДОЭ до примерно 15 минут для каскада из трех ДОЭ.

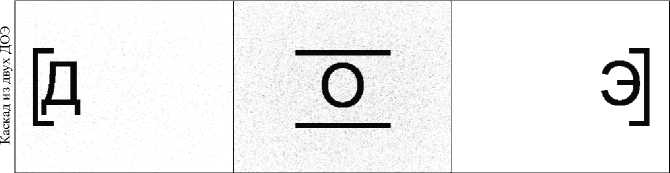
На рис. 4 представлены распределения интенсивности, формируемые рассчитанными одиночным и каскадными ДОЭ на трех заданных длинах волн. Из рис. 4 видно, что качество формируемых распределений быстро улучшается с увеличением числа ДОЭ. В частности, для одиночного ДОЭ качество сформированных распределений является весьма низким и содержит явно выраженные шумовые компоненты. При этом распределения на рис. 4 в , сформированные каскадом из трех ДОЭ, уже визуально неотличимы от требуемых распределений на рис. 2.

h , мкм

ДОЭ2 ( z = 160 мм)

ДОЭ 3 ( z = 240 мм)

Рис. 3. Рассчитанные функции высот микрорельефа одиночного ДОЭ (а), каскада из двух ДОЭ (б) и каскада из трех ДОЭ (с)

Eff = 37,24 %, 5 = 39,45 % Eff = 38,44 %, 5 = 43,65 % Eff = 48,36 %, 5 = 19,41 %

Eff = 70,39 %, 5 = 2,63 %           Eff = 71,16 %, 5 = 2,73 %           Eff = 78,08 %, 5 = 1,50 %

Eff = 88,50 %, 5 = 0,52 %           Eff = 88,51 %, 5 = 0,51 %           Eff = 91,36 %, 5 = 0,26 %

О

Рис. 4. Рассчитанные распределения интенсивности, формируемые при трех длинах волн одиночным ДОЭ (строка 1), каскадом из двух ДОЭ (строка 2) и каскадом из трех ДОЭ (строка 3). Над распределениями указаны значения энергетических эффективностей и среднеквадратичных отклонений на расчетных длинах волн

Для более точной характеристики качества формируемых распределений на расчетных длинах волн X q введем значения энергетических эффективностей Eff q и среднеквадратичных отклонений 5 q . Значение энергетической эффективности

Eff q =      JJ I n "-q ( u n * ■ ) d 2 " n + 1                       °² )

E0,q Gq соответствует доле энергии

E 0, q = ft '’0, q ( " 0 )|2 d 2 " 0

падающего пучка с длиной волны X q , которая попадает в область требуемого распределения G q = { " _п +1 | I q ( u _п +1 ) ^ 0} для данной длины волны. Значение

5 q = 4- / IT[ I n + 1, q ( " n + 1 ) - Eff, ■ I q ( " n + 1 )] " d 2 " , + 1 (13) M q _G

G q

задаёт среднеквадратичное отклонение распределения интенсивности I n+1,q ( u n +1 ), сформированного на длине волны X q , от требуемого распределения I q ( u „ +1 ). При этом указанное отклонение нормировано на среднее значение

Mq = IGq I 1 AG In+1,q ("n+1)d2"n+1, где ||Gq|| – площадь области Gq. Значения энергетических эффективностей и среднеквадратичных отклонений в процентах для рассчитанных примеров приведены на рис. 4 над каждым из сформированных распределений. Из приведенных значений можно видеть, что для каскада из трех ДОЭ значения среднеквадратичных отклонений δq составляют менее 1 %, а значения энергетических эффективностей превышают 88 %. Для понимания достижимых рабочих характеристик был также рассчитан каскад из четырех ДОЭ (для краткости не приведен в статье). Для каскада из 4 ДОЭ значения среднеквадратических отклонений падают до сотых долей процента, а энергетические эффективности превышают 96%.

В заключение настоящего параграфа отметим, что каскадные ДОЭ, по сравнению с одиночными, хотя и обладают значительно лучшими рабочими характеристиками, но в то же время являются и существенно более сложными в технологической реализации. При этом одной из главных проблем является требование к высокой точности позиционирования ДОЭ, образующих каскадный ДОЭ или ДНС [17, 18, 32, 33]. Например, в работе [32] показано, что для излучения видимого диапазона ошибки позиционирования, при которых сохраняются хорошие рабочие характеристики каскадного ДОЭ, не должны превышать размера «пикселя» дифракционного микрорельефа, т.е. составлять величину порядка нескольких микрон. При этом в настоящее время доступны высокоточные моторизованные платформы с шагом перемещений по осям координат в 1 мкм. Именно такие платформы были успешно использованы в работе [32] при экспериментальной реализации ДНС в виде каскада из пяти ДОЭ. Следует также отметить, что одним из перспективных способов «борьбы» с проблемой точности позиционирования элементов каскадного ДОЭ является использование специальных методов дизайна, учитывающих ошибки позиционирования ДОЭ [33]. Разработка таких методов для задачи расчета каскадных спектральных ДОЭ будет являться предметом дальнейших исследований.

Заключение

Рассмотрен градиентный метод расчета каскадных ДОЭ в задаче формирования нескольких заданных распределений интенсивности для нескольких падающих пучков с различными длинами волн. Задача расчета каскадного ДОЭ сформулирована как задача минимизации функционала, зависящего от функций высот дифракционного микрорельефа каскадного ДОЭ и представляющего ошибку формирования заданных распределений интенсивности на расчетных длинах волн. Для производных функционала получены явные и компактные выражения. С использованием предложенного градиентного метода рассчитаны каскадные ДОЭ для формирования трех заданных распределений интенсивности (образующих изображение надписи «ДОЭ» в рамке) для трех различных длин волн из красной, зеленой и синей частей спектра. Приведенные результаты численного моделирования показывают, что рассчитанный каскад из трех

ДОЭ формирует заданные распределения интенсивности с низкими среднеквадратическими ошибками (не более 0,52%) и высокими энергетическими эффективностями (более 88%).

Работа выполнена при поддержке Российского научного фонда (проект № 24-19-00080, разработка градиентного метода и расчет спектральных ДОЭ) и государственного задания НИЦ «Курчатовский институт» (создание программных средств для моделирования работы каскадных спектральных ДОЭ).