Градиентный метод решения задачи фокусировки в двумерную область при протяженном источнике

Задача фокусировки в двумерную область состоит в расчете формы поверхности оптического элемента из условия формирования требуемого распределения освещенности в некоторой плоскости от заданного источника. Данная задача является актуальной для большого числа приложений, включающих расчет лазерных систем фокусировки, расчет светотехнических устройств, систем освещения и т. д.

В общем случае задача формирования заданной диаграммы направленности или распределения освещенности при точечном (компактном) источнике света сводится к решению нелинейного дифференциального уравнения типа уравнения Монжа-Ампера [1-3] и является крайне сложной. Ряд методов решения задач данного класса в приближении геометрической оптики разработан для дифракционных оптических элементов [4-10]. В этом случае задача ставится как задача расчета эйконала светового поля в плоскости из условия формирования заданной интенсивности поля в некоторой области пространства. Восстановление формы поверхности рельефа дифракционного элемента по функции эйконала основано на использовании приближенных соотношений типа приближения тонкого оптического элемента. Использование подобных соотношений недопустимо при расчете зеркал и преломляющих поверхностей.

Ряд методов расчета оптических элементов разработан в светотехнике [11-14]. Методы светотехники позволяют учесть размеры и форму источника света, однако аналитические решения и эффективные алгоритмы расчета известны только для задач с радиальной симметрией. В последние годы появились публикации по расчету оптических поверхностей при точечных источниках излучения итерационными методами [15, 16]. Указанные методы позволяют сформировать сложные распределения освещенности, например, в виде алфавитно-цифровых символов, однако обладают низкой эффективностью. Кроме того, эти методы не могут быть использованы для протяженных источников.

В статье рассмотрен градиентный метод решения задачи фокусировки в заданную двумерную область при протяженном источнике. Метод позволяет реализовать фокусировку с энергетической эффективностью в 100% в области, не обладающие радиальной симметрией. Метод основан на представлении оптической поверхности через распределение эйконала светового поля в прилегающей плоскости и аппроксимации источника излучения набором точек. Эйконал определяется в виде полинома. Расчет преломляющей поверхности основан на градиентной минимизации функционала ошибки, представляющего отличие расчетной и заданной освещенностей, по коэффициентам полинома эйконала, определяющего поверхность.

Постановка задачи

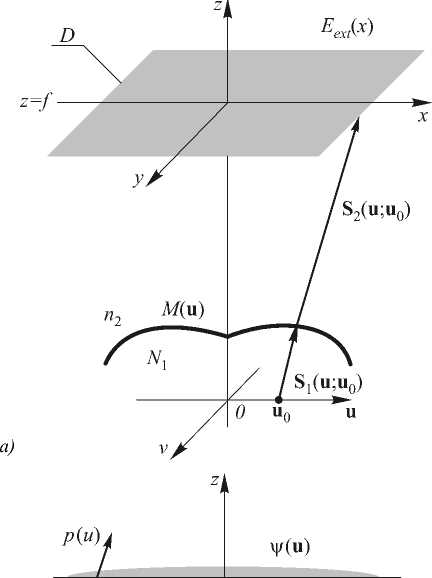
Требуется рассчитать преломляющую поверхность M из условия фокусировки излучения от протяженного источника в область D , расположенную в плоскости z = f (рис. 1 а ). Будем считать, что источник излучения расположен в плоскости z= 0, u = ( u, v ) - декартовы координаты в этой плоскости. В области D должно быть сформировано заданное распределение освещенности E ext ( x ) , x е D . Плоскость z = f и область D будем называть плоскостью фокусировки и областью фокусировки, соответственно.

Представление оптической поверхности через эйконал

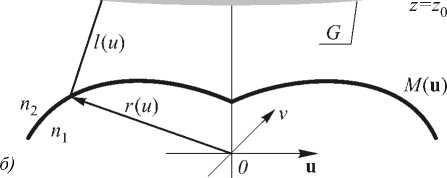
Рассмотрим точку O в центре протяженного источника. Для нее можно в некоторой плоскости на расстоянии z ₀ по оптической оси z от источника определить эйконала светового поля y ( u ) , u е G (рис. 1 б ). Область G будем называть апертурой. Определим поверхность M через функцию распределения эйконала y ( u ) .

Р ^(u ) = ( Рх ^(u ) , P y ^(u ) , P_z ^(u ) ) =

Vv( u) ,^1 -(Vy(u))2

, , (dw(u) dw(u)) где Vy(u)=        , v 2 ( dи      dv J

определяется из уравнения

Функция l ( u ) в (1)

v ( u ) = l ( u ) + n OM ( u )|,                   (3)

где n ₁ - показатель преломления материала оптического элемента, |OM ( u )| = |r ( u ) - p ( u ) l ( u ) - O| -расстояние от источника излучения до точки преломляющей поверхности. Уравнение (3) определяет условие равенства оптических длин лучей, прошедших через преломляющую поверхность, заданному эйконалу ^ ( u ) . Расчет функции l ( u ) из (3) сводится к решению квадратного уравнения

( ⁿ 1^{2 -} 1 ) ^l ( ^u ) ⁺

+2 1 ( u ) ( v ( u ) - n ² ( r ( u ) - O , p ( u ) )) +            (4)

+ n 1² |r ( u ) - O| ² - v ² ( u ) = 0.

Рис. 1. Геометрия задачи расчета преломляющего оптического элемента: формирование распределения освещенности от протяженного источника излучения в плоскости фокусировки (а); представление оптической поверхности через эйконал (б)

Представление поверхности через распределение эйконала в плоскости авторы считают удобным, поскольку оно позволяет использовать аналитические и итерационные методы расчета эйконала, разработанные для дифракционных оптических элементов [4-10].

Поверхность M ( u ) = ( M x ( u ) , M y ( u ) , M_z ( u ) ) однозначно определяется через функцию эйконала v ( u ) , u е G . Действительно, проведем расчет преломляющей поверхности по распределению эйконала v ( u ) (рис. 1 б ). Запишем уравнение преломляющей поверхности в виде

M ( u ) = r ( u ) - p ( u ) l ( u ) ,                        (1)

где r ( u ) = ( u , v , z ₀ ) - вектор точки в плоскости задания эйконала, p ( u ) - вектор направления луча, который определяется эйконалом y ( u ) , l ( u ) - расстояние от точки r ( u ) до преломляющей поверхности по направлению p ( u ) . Вектор луча p ( u ) имеет вид [17]:

Расчет освещенности от протяженного источника

Рассмотрим расчет освещенности сформированной оптической поверхностью в области D , расположенной в плоскости фокусировки z = f , в случае протяженного источника. Для вычисления освещенности аппроксимируем протяженный источник набором точечных источников излучения. В этом случае освещенность E_xt ( x ) , x е D будет равняться сумме освещенностей от точечных источников. Рассмотрим расчет освещенности E ( x ; u ₀ ) от оптической поверхности для источника в точке u ₀ = ( и ₀ , v ₀ ,0 ) (рис. 1). Исходящий луч

S 1 ( u ; u ) = ( M ( u ) - u ) / M ( u ) - u 0| ⁽⁵⁾ к поверхности (1) в точку M ( u ) из точки u ₀ . Согласно закону Снеллиуса, преломленный луч может быть представлен в виде суперпозиции исходящего единичного луча и единичного вектора-нормали к преломляющей поверхности

n

S 2 ( u ; u ) =    S ( u ; u ) +

+

^^^^^^.

— (S1 , ⁿ К ¹

^П 2

^^^^^^.

n

— S 1 х n

2 ^

n

,

^(u ) ,

где n ₂ - показатель преломления окружающей среды.

Единичный вектор-нормаль к поверхности запишем в виде:

n ^(u ) =

dM (u) dM (u) du      dv dM (u) dM (u) du      dv

Вектора-компоненты векторного произведения в (7) могут быть найдены из (1) и (4) путем прямого дифференцирования уравнений.

Таким образом, координаты прихода преломленного луча в плоскость фокусировки могут быть найдены в виде x (u; uo) = M (u) + S2 (u; u) l (u; uo), (8)

где 8 ( x ) - дельта функция. Аппроксимируем дельта функцию в (12) некоторой иглообразной функцией 8 _О ( x , у ) ( lim 8 _О ( x , у ) = 8 ( x , у ) ) и представим распределение освещенности в виде

E (x; uo )=JJMx - x (u; uo)) I (Siz )x G f dM (u) dM (u)

( du      dv

x —---------з—

|^M ( ^u ) ^-uo|

( M ( u ) - u o , n ( u ) ) d u .

где l ( u ; u _o ) = ( f - M z ( u ) ) / S ₂ z ( u ; u _o ) - расстояние

от преломляющей поверхности (1) до плоскости фокусировки по направлению преломленного луча. S ₂ z ( u ; u _o ) - z -компонента вектора преломленного луча.

Освещенность в плоскости фокусировки определяется из закона сохранения светового потока в виде

E ( x ; u o ) =

E о ( u ; u o ) I J ^(u)l

где E ₀ ( u ; u ₀ ) - освещенность, созданная поверхностью в плоскости задания эйконала, а

^{J (u ) =}

d x ( u ) d у ( u ) d u    d v

d у ( u ) d x ( u ) d u    d v

якобиан преобразования координат (5). Освещенность E _o ( u ; u _o ) также определяется из закона сохранения светового потока по формуле

^E о ( u ; ^uo ) = I ( S i z )

----------₂—— cos a, (11) |^M ( ^u ) ^-uo|

где I ( S _{1 z} ) - интенсивность точечного источника излучения в точке u ₀ (будем считать ее функцией от угла между осью Oz и исходящим лучом), S _{1 z} –

z -компонента вектора испущенного луча,

cos(a)=

M ( u ) - u o , n ( u )

|^M ( ^u ) ^-uo| ""

Представление для освещенности (9) неудобно для расчета, поскольку его нельзя использовать в области каустик, а также в случае, когда несколько лучей из плоскости задания эйконала приходят в одну точку области фокусировки. Для нахождения удобной расчетной формулы для распределения освещенности E ( x ; u ₀ ) , воспользуемся интегральным представлением формулы (6)

^E ( x ; u o WJX ^{x - x} ( u ; u o ) ) ^E о ( u ; u o ) d u , ⁽¹²⁾ G

Выражение (13) ориентировано на расчет освещенности с использованием метода трассировки лучей. В этом случае формула (13) дает усредненное значение освещенности по окрестности, определяемой «эффективной» шириной функции 5 _О ( x , у ) . Величина этой окрестности обычно определяется шагом дискретизации в области наблюдения. В качестве функции 5 _a ( x , у ) может, например, использоваться гауссова функция

z х 1 f x ² + у y М x , У ) = —yexpl--—

ПО ( с

В этом случае освещенность (13) будет усредненным значением освещенности (12) с Гауссовым весом (14). Выбор о в (14) зависит от величины шага дискретизации области фокусировки. В экспериментах использовалось значение о равное половине максимального шага дискретизации. Выражение (13) позволяет записать результирующую освещенность от набора из L точечных источников u _{0 i} в плоскости фокусировки

L

E xt. ( x ) = Е ^E ( x ; u o - ) .                             ⁽¹⁵⁾

i = 1

Когда протяженный источник излучения задан поверхностной яркостью B (S1 z, uo) , результирую-

щую освещенность можно записать в виде четырехкратного интеграла

E -( x ) = [Ш B ( ^S-- u « )

G

^{x -} x ( u ; u o ) )

-----------x (16)

I^M ( ^u ) ^-uo|

x ( M ( u ) - u _o , n ( u ) ) d ² u d ² u _o .

Расчет оптической поверхности для фокусировки в заданную область

Для расчета преломляющей поверхности M ( u ) , формирующей заданное распределение освещенности, был использован градиентный метод минимизации функционала ошибки s ( v ) , представляю-

щего отличие расчетного и требуемого распределений освещенности в плоскости фокусировки.

При этом поверхность и распределение освещенности считаются представленными через эйконал поля в плоскости z = z 0 согласно формулам (1), (2), (4), (8), (9), (16). Такое представление является удобным для расчета начального приближения.

Рассмотрим использованный градиентный метод. Определим эйконал в виде полинома

^ ( u , v ) = j^c_v u i v ^j ■                             (17)

Полиномиальное представление эйконала было использовано в работах [18, 19] и показало хорошие результаты при расчете эйконала из условия фокусировки в заданные области. В этом случае задача минимизации функционала ошибки s ( y ) сводится к задаче минимизации функции многих переменных от коэффициентов c_ij . В качестве функции невязки была использована квадратичная функция

^E ( c ) = jj ( E ext ( x c ) - E ext ( ^x ) )² d x ^d У,              ⁽¹⁸⁾

D где вектор c обозначает набор коэффициентов полинома, а Eext (x; c), Eext (x) - расчетное и требуемое распределения освещенности в области фокусировки. В этом случае градиентный расчет функции преломляющей поверхности состоит в итерационной коррекции вектора коэффициентов c по правилу cn = cn-i -tVs(cn-i), где Vs(c) - градиент функции невязки, t - шаг метода. Компоненты вектора градиента в (19) несложно получить в виде

^^(c) = 2jJ(Eext (x; c)- Eext (xЖ (x) d2x,(20)

d cijD где

^ j ( x ) = JJJJ B ( S i z , U o ) S i z ^x G

Г d M ( u ; c ) d M ( u ; c ) )

( du        дv J

X                   ~      X                     /a n

| M ( u ; c ) ^- u o|

x( M (u; c)- u0, n (u; c))x x^-(Mx -x (u; uo;c))) d2u d2uo, d cij где x (u; u0; c) - координаты лучей (8) в плоскости фокусировки.

Расчет вектора градиента также может осуществляться численно с использованием разностных ,                                        ds _    _ формул для расчета производных дт^ ■ В работе, для минимизации функции ошибки (18) и реализации градиентного метода (19) были использованы java-класс Uncmin_f77 и java-интерфес Uncmin_methods из пакета оптимизации «AN UNCONSTRAINED NONLINEAR OPTIMIZATION SOLVER».

Результаты расчета

Для характеристики качества решений, получаемых в результате работы итерационного алгоритма, введем значения энергетической эффективности e и среднеквадратичной ошибки 5. Значение e = J Eext (x) d2x/J Eo (u) d2u, (22) DG где E0 (u) - освещенность, сформированная оптическим элементом в плоскости эйконала, характеризует долю энергии, фокусируемую в требуемой области D.

Значение

^X E ||D ||^J( E ^{ext (} x ; c ) E ^{ext (} x ) ) d x ,

D

где D – площадь области фокусировки D, а E – среднее значение, характеризует ошибку формирования заданного распределения освещенности ^Eext ( ^x ) ^.

Рассмотрим расчет оптической преломляющей поверхности, формирующей заданное распределение освещенности, при точечном и протяженном источниках излучения. Необходимо рассчитать преломляющий элемент для фокусировки излучения в квадрат со стороной 60 мм. Плоскость фокусировки находится на расстоянии 30 мм от преломляющей поверхности. В случае протяженного источника, он представляет собой квадратную площадку со стороной 1 мм. И точечный, и протяженный источники излучают по ламбертовскому закону. Расстояние от источника до преломляющего элемента 3 мм. Апертура преломляющего элемента – круглая.

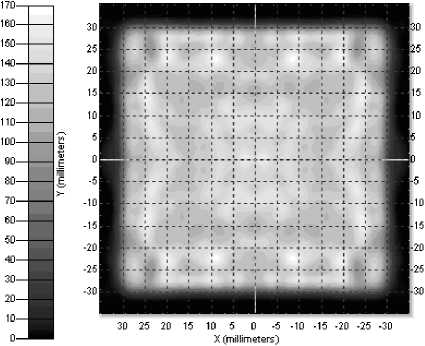
Для расчета поверхности при точечном источнике излучающий элемент необходимо аппроксимировать только одной точкой. Для определения поверхности был использован эйконал в виде полинома от 8 переменных в круговой области с радиусом 2,5 мм. Из-за симметричности задачи, число переменных минимизации составило 6. Энергетическая эффективность фокусировки составила 100% при среднеквадратичной ошибке x=5,6%. При помощи специализированной программы по светотехнике TracePro [20] для 100000 лучей было рассчитано распределение освещенности в плоскости фокусировки при точечном источнике (рис. 2). Отметим, что программа TracePro не решает обратных задач расчета поверхностей, а позволяет только моделировать работу оптических систем по методу трассировки лучей. Как видно из рис. 2, форма и характер распределения соответствуют требуемым.

На рис. 3 представлено распределение освещенности, полученное от протяженного источника с рассчитанным преломляющим элементом. Распределение имеет сильно выраженный неравномерный и размытый характер. Среднеквадратичная ошибка составила 37,3%, эффективность фокусировки – 60%. Таким образом, в данном случае нельзя решать задачу в приближении для точечного источника освещенности.

Для коррекции полученного решения был использован описанный градиентный метод расчета оптических поверхностей для протяженных источников света. Заданный источник аппроксимировался набором из 4 точек. Эйконал, представляющий поверхность, также задавался в виде симметричного полинома 8-ой степени в круговой области с радиусом 2,5 мм. Полученная прелом- ляющая поверхность представлена на рис. 4. Для рассчитанной поверхности энергетическая эффективность фокусировки составила 99% при среднеквадратичной ошибке χ=13,4%. Моделирование элемента с оптимизированной поверхностью было проведено трассировкой 100000 лучей. Результат расчета представлен на рис. 5. Полученная среднеквадратичная ошибка почти в 3 раза меньше, чем в предыдущем примере, качество фокусировки высокое.

Приведенные примеры показывают эффективность разработанного градиентного метода для задачи расчета преломляющих оптических элементов для фокусировки в заданные двумерные области при протяженных источниках освещения.

Total - Illuminance tvbp for Absorbed Flux

Object 2 Surface 1 lux                  30 25 20 15 10 5 0 -5 -10 -15 -20 -25 -30

Illuminance Mn:0.0014443 lux, btax:168.32 lux, Аме:96.748 lux,

RMS:55.083, Normalized Flux:0.47406 20278 Incident Rays

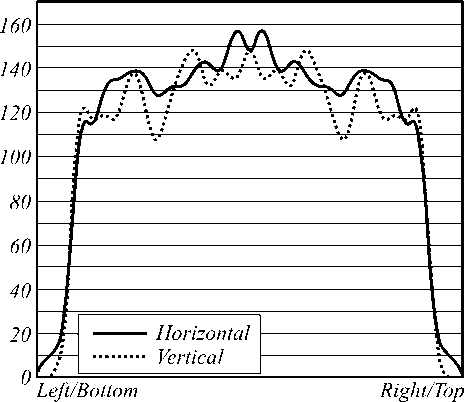
Рис. 2. Рассчитанная освещенность от точечного источника излучения с оптимизированным для него элементом (а); горизонтальное и вертикальное сечения распределения освещенности (б)

Total - Illuminance tutap tor Absorbed Flux

Object 2 Surface 1 lux                   30 25 20 15 10 5   0 -5 -10 -15 -20 -25 -30

а)

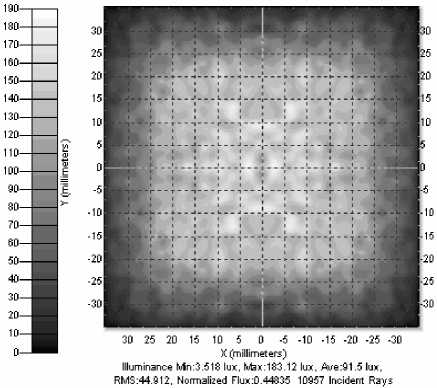
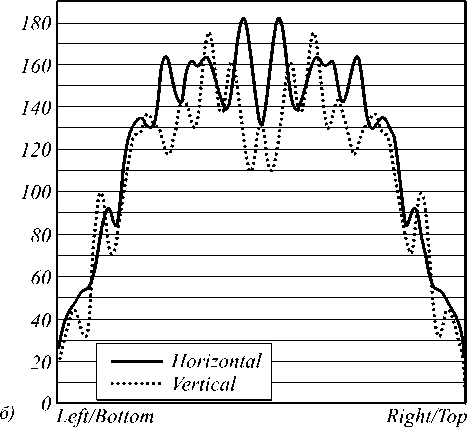
Рис. 3. Рассчитанная освещенность от квадратного источника излучения со стороной 1 мм с преломляющим оптическим элементом

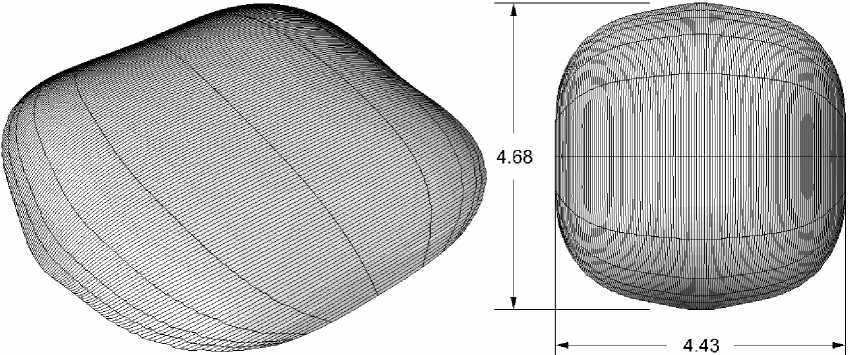
Рис. 4. Преломляющая поверхность для фокусировки в квадратную область со стороной 60 мм в плоскости фокусировки f=30 мм для квадратного источника излучения со стороной 1 мм

Total - Illuminance Ivfap for Absorbed Flux

Object 3 Surface 1

■5 -10 -15 -20 -25 -30

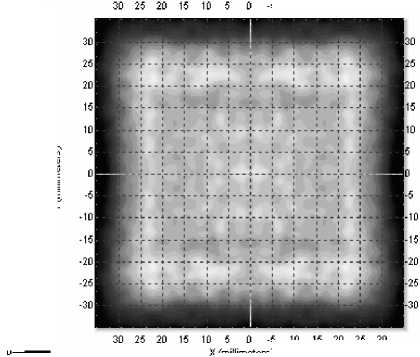
а)

-5 -1U -15 -20 -25 -30 X (millimeters)

Illuminance Mn:0.0008644 lux, IVfex:171.17 lux, Are: 91.854 lux, RMS :50.829, Normalized Flux :0.45009 23473 Incident Rays

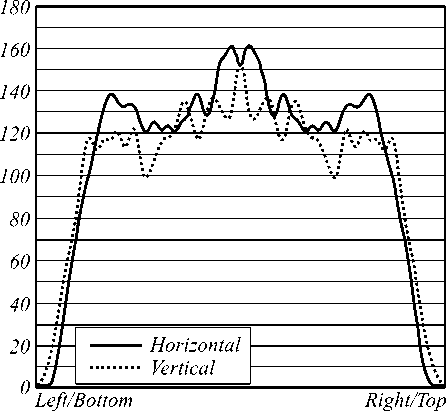
Рис. 5. Рассчитанная освещенность от квадратного источника излучения со стороной 1 мм с оптимизированной для него преломляющей поверхностью

Заключение

Рассмотренный метод расчета преломляющих поверхностей, представленных через эйконал поля применим для расчета оптических элементов при точечных и протяженных источниках излучения. Метод показал высокое качество фокусировки в заданную двумерную область: среднеквадратичную ошибку (6-13%) при 100% энергетической эффективности. Предложенный метод можно использовать для расчета отражающих поверхностей. При расчете отражающих поверхностей изменится только уравнение (4), описывающее восстановление поверхности по эйконалу в плоскости.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-Sa-06) и грантов РФФИ № 07-07-

97601-р_офи, 07-01-96602-р_поволжье_а, 07-07-91580-АСП_а.