Графическая интерпретация задачи линейного программирования при оптимизации процесса функционирования зерноуборочного комбайна «Вектор»
Автор: Джигарханов Дмитрий Георгиевич, Трасковский Сергей Станиславович
Журнал: Вестник аграрной науки Дона @don-agrarian-science
Рубрика: Механизация и электрификация животноводства, растениеводства
Статья в выпуске: 3 (15), 2011 года.
Бесплатный доступ
С точки зрения графической интерпретации предложено решение задачи оптимизации процесса функционирования зерноуборочного комбайн по критерию производительности. Аналогично можно проводить графические исследования с различными параметрами, например, в качестве целевой функции можно выбирать минимум потерь или дробления зерна, а в качестве ограничений использовать производительность, расход топлива.
Испытания, регрессионный анализ, задача линейного программирования, симплекс-метод, градиентный метод, зерноуборочный комбайн
Короткий адрес: https://sciup.org/140204102
IDR: 140204102 | УДК: 631.173.6
Graphic interpretation of a problem of linear programming by optimization of process of functioning of a combine harvester «Vector»
From the point of view of graphic interpretation the decision of the optimization problem of functioning grain-harvesting combine process by criterion of productivity is offered. It is similarly possible to carry out graphic researches with various parametres, for example, as criterion function it is possible to choose a minimum of losses or grain crushing, and as restrictions to use productivity, the fuel expense.
Текст научной статьи Графическая интерпретация задачи линейного программирования при оптимизации процесса функционирования зерноуборочного комбайна «Вектор»
Введение. В задачах линейного программирования (ЛП) рассматривается нахождение экстремумов функций линейно зависящих от своих аргументов при линейных ограничениях. При этом ограничения max(min): L = c 1 x 1 +
могут записываться как в виде равенств, так и виде неравенств.
В общем виде задача ЛП может быть записана так:
c 2 x 2 + ... + c n x n , i = 1, n, (1)
при ограничениях: a11x1 + … + a1nxn = b1, ap1x1 + … + apnxn = bp,
a p+11x1 + … + a p+1nxn ≤ bp+1, am1x1 + … + amnxn ≤ bm; p = 1, m; .xi ≥ 0; bp ≥ 0.
Постановка задачи. Нами получены результаты эксплуатационно-технологической оценки зерноуборочных комбайнов «Вектор» на «Сев.-Кав. МИС» на уборке озимой пшеницы прямым комбайнирова-нием (табл. 1).
Кодирование основных параметров и показателей зерноуборочных комбайнов представлено в таблице 2. При этом была поставлена задача – оценить по результа-
там испытаний эффективность процесса функционирования комбайнов «Вектор» в условиях ЮФО.
Результаты решения. Используя регрессионный анализ по результатам испытаний зерноуборочных комбайнов «Вектор» на «Сев.-Кав. МИС» (см. табл. 1), модель процесса функционирования зерноуборочного комбайна «Вектор» в аналитическом виде может быть представлена [1, 2]:
Var 9 = 0,13176 Var1 + 1,085928 Var26,
Var 16 = 0,0157 Var1 + 0,1748 Var26,
Var 17 = 0,0086 Var1 + 0,2481 Var26,
Var 18 = 0,0069 Var1 + 0,12204 Var26,
Таблица 1
Результаты испытаний комбайна «Вектор» на «Сев.-Кав. МИС» на уборке озимой пшеницы прямым комбайнированием
|
Var1 |
Var2 |
Var3 |
Var4 |
Var5 |
Var7 |
Var9 |
Var10 |
Var11 |
Var13 |
Var14 |
Var15 |
Var16 |
Var17 |
Var18 |
Var19 |
Var20 |
Var21 |
Var26 |
Var29 |
Var30 |
Var31 |
Var35 |
Var36 |
Var37 |
Var50 |
|
|
1 |
52,6 |
1,3 |
12,6 |
23,7 |
0,71 |
41,5 |
12,3 |
9,1 |
8,6 |
0,74 |
0,7 |
1,87 |
1,45 |
1,55 |
1,21 |
2,3 |
11,9 |
12,67 |
4,1 |
12 |
23,7 |
1,1 |
18,4 |
0,42 |
0,87 |
11-34-04 |
|
2 |
36 |
0,5 |
16 |
10,2 |
1,25 |
41,1 |
10,1 |
7,2 |
7,1 |
0,71 |
0,7 |
1,9 |
1,47 |
1,5 |
0,6 |
2,24 |
8 |
15 |
4,9 |
11 |
21,2 |
0,9 |
13,2 |
0,43 |
0,73 |
11-30-05 |
|
3 |
48,8 |
1,6 |
13,1 |
14,1 |
0,71 |
34,4 |
9,8 |
7,3 |
7,1 |
0,74 |
0,72 |
1,92 |
1,46 |
1 |
8 |
2,77 |
13,6 |
11,4 |
3 |
12,2 |
26,7 |
0,8 |
12,3 |
0,46 |
0,74 |
11-33-06 |
|
4 |
30,8 |
3,9 |
9,8 |
15,4 |
0,91 |
40,6 |
10,1 |
7,2 |
6,8 |
0,72 |
0,67 |
1,93 |
1,47 |
1,7 |
1 |
2.9 |
9 |
13,3 |
5,7 |
9,8 |
21,8 |
0,5 |
11,5 |
0,46 |
0,6 |
11-15-07 |
|
5 |
57,8 |
3,3 |
10,2 |
28 |
0,71 |
41,7 |
10,9 |
7,5 |
7,1 |
0,71 |
0,67 |
1,89 |
1,44 |
1,38 |
0,5 |
2,55 |
14,7 |
14,3 |
3,16 |
12 |
19,5 |
0,7 |
14,5 |
0,45 |
0,98 |
11-19*-08 |
Таблица 2
Кодирование основных параметров и показателей зерноуборочных комбайнов
max:Var9 = 0,13176 Var1 + 1,085928 Var26, (3)
при ограничениях:
Var16 = 0,0157 Var1 + 0,1748 Var26 ≤ 1,5,
J Var17 = 0,0086 Var1 + 0,2481 Var26 ≤ 2,0, (4)
Var18 = 0,0069 Var1 + 0,12204 Var26 ≤ 2,0,
20 ≤ Var1 ≤ 50, 3 ≤ Var26 ≤ 5.
Для решения задачи ЛП (3), (4), например симплексным методом (СМ), требуется преобразование задачи в матричную форму [2] (рис. 1).
fl RRR - AkelPad
|
Файл Правка Вид Настройки |
Кодировка Справка |
|
FILE: ОРТ Sun Jul 12 |
2009 12:24:54 AM Pagel |
|
Row х1 х2 |
хЗ хЗ х4 |
|
1 0.131760 20.0 2 1.085928 58.8
Ъ |
1.00000Е0 0.00000 1. 1.00000Е0 0.00000 -1. 0.00000Е0 1.00000 1. 0.00000Е0 1.00000 -1. 1.57200Е-2 0.17480 1. 1.57200Е-2 0.17480 -1. 8.62000Е-3 0.24810 1. 8.62000Е-3 0.24810 -1. 6.93000Е-3 0.12204 1. 6.93000Е-3 0.12204 -1. |
Рис. 1. Матричная форма задачи ЛП (3), (4)
2< Lister - LC:\ Documents and Settings\Admin\Mon документы\ВТУЗ\Наука\
Файл Правка Вид Справка Sun Jul 12 2009 12:23:39 AM
|
Final solution |
reached aF t er 8 p iи о 1 |
|
|
Haximun value |
oF objective Function |
- 11.0237 |
|
uariable |
value |
|
|
X 1 |
50-0000000 |
|
|
X 2 |
U_0846682 |
|
|
slack |
value |
|
|
S 2 |
- 00000000 |
|
|
s u |
_91533181 |
|
|
S 6 |
- 00000000 |
|
|
s 8 |
- 55559382 |
|
|
S 10 |
1 -15 5 0 07 09 |
|
|
surplus |
value |
|
|
S 1 |
30-00O0000 |
|
|
S 3 |
1 - 0846682 |
|
|
S 5 |
1 - 4000000 |
|
|
S 7 |
1 - 3 444 06 2 |
|
|
S 9 |
_7449929 |
|
|
constraint |
shadow price |
|
|
C 1 |
- 00000000 |
|
|
C 2 |
- 0341 01 03 |
|
|
C 3 |
_00000000 |
|
|
C U |
- 00000000 |
|
|
С 5 |
- 00000000 |
|
|
C 6 |
6.21240275 |
|
|
C 7 |
- 00000000 |
|
|
C 8 |
- 00000000 |
|
|
C 9 |
- 00000000 |
|
|
C 10 |
- 00000000 |
Рис. 2. Решение задачи ЛП (3), (4) симплексным методом
Само решение задачи СМ, представленное на рисунке 2, свидетельствует, что при правильной настройке комбайнов «Вектор», выполнении всех ограничений на агрофон по ТУ и отсутствии непредвиденных остановок, связанных с поломками и непроизводственными потерями времени, производительность комбайна «Вектор» (по зерну) за час основного времени в условиях при ограничениях:
a 11 x 1 + a 12 x 2 ≤ b 1 ,
ЮФО может достигать Var9 = 11 т/ч, а за час эксплуатационного времени Var11 = 7,7 т/ч, при этом комбайн не рассчитан на уборку зерновых с урожайностью выше 50 ц/га.
Когда число неизвестных равно 2 (n = 2, 3), общая задача ЛП (1), (2) будет иметь вид max(min): L = c1x1 + c2x2 , i = 1, 2, (5)
a m1 x 1 + a m2 x 2
≤ b m ; p = 1, m; .x i ≥ 0; b p ≥ 0.
Допускает графическое толкование (рис. 3).
Графическая интерпретация задачи ЛП по результатам испытаний комбайнов «Вектор»
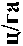
220,0000
200,0000
180,0000
160,0000
140,0000
120,0000
100,0000
80,0000
60,0000
40,0000
20,0000
0,0000
-20,0000
-40,0000
Скорость движения, км/ч
Рис. 3. Графическая интерпретация задачи (3), (4).
Для решения задачи воспользуемся градиентным методом, для этого определим полуплоскости, где выполняются условия неравенств (4), (6) и область G допустимых решений. Среди точек допустимой области G, для нахождения max: L можно использовать градиент grad L = (c 1 ,c 2 ) т , компонентами которого явля-
ются частные производные функции по ее аргументу. Градиент направлен в сторону наискорейшего возрастания функции и перпендикулярен к линии уровня, проведенной в точке, где он вычисляется, grad Var9 = (0,13176, 1,085928). Перемещая линию уровня параллельно самой себе до тех пор, пока она не займет крайнее положение
в области G. Точка области G, через которую проходит линия уровня в крайнем положении, и будет max:Var9.
Выводы. Таким образом, из рисунка 3 следует, что комбайн «Вектор» может использоваться и при более высокой урожайности зерновых, чем, например, 50 ц/га, но при этом будет снижаться его производительность, а что касается рабочей скорости комбайна, то она не должна превышать 8 км/ч.
Аналогично можно проводить графические исследования с различными параметрами, например, в качестве целевой
функции можно выбирать минимум потерь или дробления зерна, а в качестве ограничений использовать производительность, расход топлива и т.п.
Список литературы Графическая интерпретация задачи линейного программирования при оптимизации процесса функционирования зерноуборочного комбайна «Вектор»
- Карманов, В.Г. Математическое программирование/В.Г. Карманов. -Москва: Наука, 1986. -288 с.
- STATISTICAL GRAPHICS SYSTEM by STATISTICAL GRAPHICS CORPORATION. User's guide. (Пакет прикладных программ STATGRAPHICS (SG), версии 2.6, номер 1157855, 1989).
