Графические зависимости для определения температуры и напряженности электрического поля в дуговом разряде

При разработке и оптимизации новых электродуговых устройств и технологий необходима информация об энергетическом состоянии разрядной плазмы. Экспериментальное исследование и измерение энергетических параметров требует очень значительных материальных и временных затрат. Расчетное определение параметров разрядов проводится с помощью вычислительных моделей различной степени сложности, основанных на совместном численном решении систем уравнений газовой динамики и электродинамики [1–4]. Такие задачи, как правило, являются ресурсоемкими, требуют мощных вычислительных средств и больших временных затрат на разработку и тестирование. По этим причинам остается актуальным применение более простых одномерных математических моделей, позволяющих оперативно рассчитывать основные параметры дуговых разрядов. С помощью такой математической модели на основе уравнения Эленбааса-Хеллера были исследованы особенности формирования дугового разряда в теплопроводном и радиационных режимах [5, 6]. Также были рассчитаны и построены на плоскости lg I – R изолинии для заданных характерных соотношений интегральных и удельных мощностей механизмов теплопроводности и излучения в разряде и определены соответствующие им зависимости температуры и напряженности электрического поля для различных газов [7–9]. Эти зависимости, прежде всего, устанавливали границы диапазонов влияния и доминирования энергетических механизмов и давали возможность определять значения параметров разряда, соответствующие этим граничным состояниям. Однако для промежуточных энергетических состояний, особенно вдали от границ, проводить оценку значений параметров разряда с помощью зависимостей для граничных состояний достаточно сложно. Графические зависимости, представленные в данной работе, дают возможность определения температуры и напряженности электрического поля с меньшей погрешностью в более широком диапазоне значений радиуса и силы тока.

Постановка задачи

Для расчета распределения температуры в осесимметричном разряде использовано уравнение Эленбааса-Хеллера, описывающее баланс энергетических механизмов джоулевой диссипации, теплопроводности и излучения

-I rX—1 + qj -qR = 0,

где r – радиус; T – температура; λ – коэффициент теплопроводности газа; q J = σE² – мощность джоулевой диссипации; q – объемная мощность радиационных энергопотерь. Уравнение (1) дополняется граничными условиями в центре разрядной области и на внешней границе

dT d J

^{0 ,} [ T ] r = R T 0 ■

Напряженность электрического поля E зависит от силы тока и распределения электропроводности σ(r) по радиусу:

R

E = I / 2 n j o ( r ) rdr. (3) 0

Электрические дуги при поперечном размере высокотемпературной зоны порядка 1 см имеют малую оптическую толщину, поэтому для расчета величины q_R было использовано приближение объемного излучателя [5].

Решение краевой задачи (1) – (3) проводилось численно с учетом температурных зависимостей свойств газов, которые вводились в программу в виде таблиц для степеней черноты &(T) , коэффициентов электропроводности o( T ) и теплопроводности X(T). Коэффициенты черноты воздуха взяты в [10, 11], аргона в [12], углекислого газа в [11], водорода в [13]. Транспортные свойства воздуха в [14], аргона в [15], углекислого газа в [16], водорода в [17, 18].

Результаты расчетов

Вычислительная модель позволяет рассчитать структуру и параметры разряда для разных газов при различных значениях силы тока I и радиуса расчетной области R . Из решения уравнений (1)–(2) определяется распределение температуры и электропроводности, с помощью формулы (3) рассчитывается напряженность электрического поля E . Для проверки адекватности вычислительной модели проведено сравнение расчетных и экспериментальных данных. На рис. 1 приведены результаты измерений температурного распределения в дуговом разряде, горящем в углекислом газе [19]. Температурный профиль дуги определяли несколькими спектроскопическими методами, ошибки в измерении температуры составляли 6–7 %. На график с обобщенным экспериментальным профилем (кривая 1) наложено расчетное распределение температуры (кривая 2). Расчетное значение температуры на оси разряда T max = 10,54 кК и отличается от измеренного примерно на 4 %, в периферийной части разряда разница увеличивается, по-видимому, из-за влияния обдува дуги, необходимого для ее пространственной стабилизации. Такое отличие в значениях T max находится в пределах ошибки

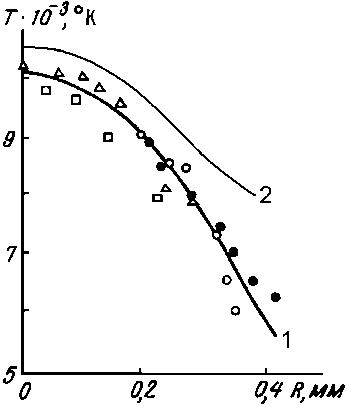
Рис. 1. Радиальное распределение температуры в разряде при R = 1 мм измерений температуры и погрешности расчета теплофизических свойств газов, которая, по мнению авторов работ [10–18], составляет от нескольких процентов до 20–30 %. Данный расчет структуры разряда был проведен при величинах пространственного шага в 0,05 и 0,025 мм, при этом различие в значении Tmax для этих двух вариантов было зафиксировано незначительным (≈ 0,02 %).

Важнейшими характеристиками дугового разряда являются температура и напряженность электрического поля. От величины температуры в столбе разряда зависят переносные свойства плазмы и интенсивность взаимодействия с электромагнитным полем, а напряженность электрического поля определяет мощность, необходимую для компенсации энергопотерь и поддержания разряда. Для определения характеристик разряда были проведены расчеты в достаточно широком диапазоне значений радиуса R = 2 ÷ 40 мм и силы тока I = 1 ÷ 10 000 А. На основе расчетов построены в виде изолиний графические зависимости T max и E на плоскости lg I – R для разряда в воздухе, аргоне, углекислом газе и водороде при атмосферном давлении. Значения на изолиниях T max приведены в кК, на изолиниях E в размерности кВ/м. Расчеты проведены при величине пространственного шага 0,5 мм, при необходимости величина шага снижалась до 0,1 мм.

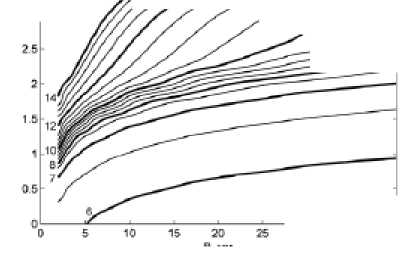
Графические зависимости для воздуха представлены на рис. 2. Изолинии максимальной температуры в центре разряда T max отображены с шагом 0,5 кК (рис. 2 а ). Поскольку на рис. 2 изолинии расположены достаточно близко друг к другу, значения температуры в кК даны только для части изолиний, имеющих увеличенную толщину. Изолинии напряженности электрического поля E построены с переменным шагом (рис. 2б). При малых значениях E изолинии имеют две ветви, которые имеют угол наклона противоположного знака. Ветви соответствуют разным режимам теплоотвода из столба разряда: нижние расположены к области, где преобладает теплопроводный механизм, верхние лежат в зоне доминирования излучения. В месте перегиба изолиний влияние теплопроводного и радиационного механизмов в энергобалансе разряда является соизмеримым.

На рис. 3 приведены характеристики дугового разряда в аргоне. Изолинии максимальной температуры T max также отображены с шагом 0,5 кК, значения на изолиниях даны с шагом 1 кК

а)

Рис. 2. Изолинии температуры (а) и напряженности электрического поля (б) для разряда в воздухе

б)

(рис. 3 а ). Изолинии напряженности электрического поля E приведены с переменным шагом. При сравнении характеристик разряда в воздухе и аргоне для изолиний T max в аргоне следует отметить более равномерное и упорядоченное расположение, а для напряженности электрического поля характерны существенно меньшие значения.

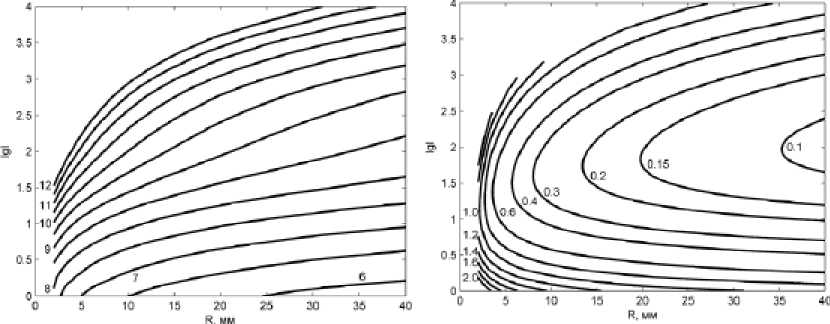
Особенностью графических зависимостей для разряда в углекислом газе является наличие достаточно протяженных горизонтальных участков изолиний T max и E в диапазоне больших значений радиуса и малых значений силы тока, которому соответствует правая нижняя часть плоскости lg I – R (рис. 4). На горизонтальных участках изолиний характеристики разряда не зависят от его радиуса. Данная особенность разряда в СО₂ ранее была отмечена и исследована в [8], где была установлена ее причина – эффект экранирования теплопроводного механизма вблизи внешней границы разряда. Этот эффект обусловлен высокими значениями степени

а)                                                      б)

Рис. 3. Изолинии температуры (а) и напряженности электрического поля (б) для разряда в аргоне

а)

Рис. 4. Изолинии температуры (а) и напряженности электрического поля (б) для разряда в углекислом газе

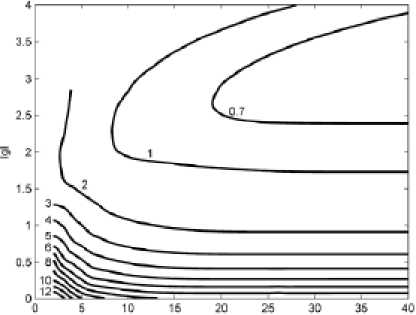
R. мм

б)

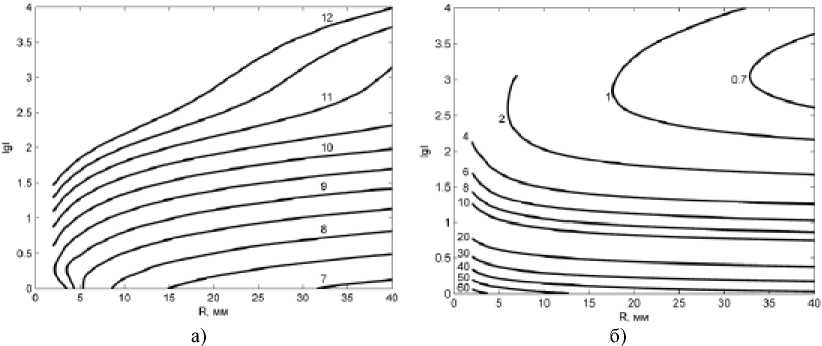
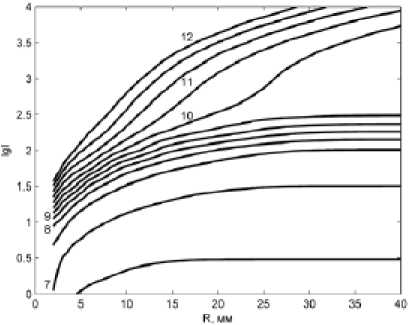
Рис. 5. Изолинии температуры (а) и напряженности электрического поля (б) для разряда в водороде черноты СО2 в диапазоне низких температур (1–2 кК), при этом периферийный слой газа с такой температурой, имеющий высокую излучающую способность, отводит всю подводимую от центральной горячей зоны теплоту за пределы разряда путем радиационного механизма, фактически экранирует центральную высокотемпературную зону разряда от теплопроводного теплообмена с внешней стенкой и тем самым обеспечивает пространственную локализацию столба разряда.

Характеристики дугового разряда в водороде отображены на рис. 5. Отличительной особенностью разряда в водороде является существенно более высокие значения напряженности электрического поля, особенно в области малых значений силы тока. Это обусловлено большим значением коэффициента теплопроводности. Так, зависимость λ( T) для водорода имеет локальный максимум λ max = 15.1 Вт/(м∙К) при 4 ∙ 10³ К, а значения λ max для воздуха и углекислого газа находятся на уровне 4 Вт/(м∙К) при T = 7 ∙ 10³ К. Таким образом, повышенная мощность теплопроводных энергопотерь для разряда в водороде компенсируется за счет большей напряженности электрического поля.

Заключение

В работе представлены в виде диаграмм на плоскости lg I – R характеристики равновесной электродуговой плазмы для некоторых технически важных газов. Графические зависимости для гелия были приведены в [9]. Демонстрируемые графические зависимости дают общую картину энергетического состояния электродуговой плазмы и позволяют оперативно оценивать температуру, напряженность электрического поля и энергетические затраты в осесимметричном стационарном дуговом разряде, горящем в воздухе, аргоне, углекислом газе и водороде при атмосферном давлении, в широком диапазоне значений радиуса и силы тока.