Графический подход к решению проблемы доступности получения визуальной информации оператором из кабины подъемно-транспортной машины

Координирующим звеном в сложных человеко-машинных системах обычно является человек, основными функциями которого являются управление машиной и контроль её работы. Операторам подъёмно-транспортных машин (ПТМ) приходится работать в жестких производственных условиях при наличии помех (от помех, вызванных метеоусловиями, до конструктивных, связанных с недостатками машин и оборудования), в непрерывно меняющейся обстановкена производственной площадке, в условиях высокой ответственности за безопасность производства работ. Увеличение числа управляемых и наблюдаемых объектов приводит к росту объёма информации, которую оператор должен принять и переработать, а затем выдать решение, что приводит к росту психофизиологических нагрузок. Этот человеческий фактор не всегда должным образом учитывается при проектировании различных машин, технические характеристики всё более усложняющихся систем довольно плохо согласуются с возможностями человека.

Человеческий фактор, определяющий зачастую выходные свойства системы, принимается во внимание только уже в процессе эксплуатации машины, а не на этапе её проектирования. Недооценка этого фактора существенно снижает надёжность функционирования системы «оператор-машина-среда» (ОМС).

В данной статье рассматривается вопрос о разработке имитационных моделей, позволяющих решать задачи оптимального проектирования конструктивных особенностей кабины строительной машины, а именно формы и площади прозрачных ограждений, положения сиденья в кабине для обеспечения доступности получения визуальной информации.

Известно, что ошибочные действия оператора строительного крана в значительной степени зависят от условий приёма информации, необходимой для упорядоченного развития системы ОМС. Около 90% информации о ходе производственного процесса оператор ПТМ получает в процессе слежения с помо- щью зрительного аппарата. В результате ошибочных действий оператора, вызванных получением недостоверной информации, в системе «оператор – машина – среда» увеличивается энтропийная тенденция, что приводит к несчастным случаям на производстве.

С целью обеспечения устойчивости развития системы ОМС необходимо создать такие условия управления машиной, при которых сочетались бы технические свойства «машины» и физиологические возможности «оператора».

Одним из условий устойчивого развития системы ОМС является возможность фиксировать объект наблюдения, как находящийся в покое, так и двигающийся непредсказуемым образом, зрительным аппаратом оператора, находящегося на рабочем месте в проектном положении с учётом оптимальных физиологических возможностей зрительного анализатора и опорно-двигательного аппарата (ОДА).

Зрительный аппарат имеет с точки зрения механики управляемого тела двойственную природу [1]. Во-первых, он является источником необходимой информации для развития (движения) системы ОМС. Во-вторых, он сам является управляемой системой тел, движение которой направлено на достижение определённых целей.

Рассмотрим вопрос возможности программирования движений зрительного аппарата, что позволит исследовать соответствие физиологических возможностей человека конструктивным особенностям кабины и её оснастки, а также характеру производимых оператором работ, выявить динамические погрешности в измерительной процедуре человека-оператора, влияющие на устойчивость системы ОМС в целом.

Зрительный аппарат в грубом приближении можно моделировать при помощи трех твердых тел: головы и двух глазных яблок (рис. 1, табл.1).

Голова – верхний, обособленный от туловища, отдел тела человека. Вследствие обособленности шейного отдела тела и развития гибкого сочленения черепа с позвоночником голова человека обладает высокой степенью подвижности. Атланто-затылочный сустав представляет собой кольцеобразный первый шейный позвонок, сочленяющийся с черепом. Посредством атланто-затылочного сустава возможно осуществление наклонов головы вверх и вниз, то есть в сагиттальной плоскости, и наклоны головы в стороны, что оператору приходится делать крайне редко при выполнении наблюдения за ходом строительномонтажных работ. Помимо подвижности в затылочном суставе голова может поворачиваться вместе с атлантом вокруг вертикальной оси, проходящей через зубовидный отросток второго (осевого) шейного позвонка – эпистрофея. Этот атланто-осевой сустав образован передней дугой атланта и зубом осевого позвонка [1].

Таблица 1 – Опорныекоординаты центров инерции головы и глаз

Звено	Центр инерции	Опорные координаты
Голова	Ц 1	x i , y i , z i , 9 ix , 9 iy , 9 iz
Левый глаз	Ц 2	x 2 , y 2 , z 2 , 9 2x , , 9 2z
Правый глаз	Ц3	Х з , У 3 , Z 3 , 9 зх , , 9 зг

Поворот головы вокруг любой из названных осей происходит в результате сокращения одних и растяжения других групп мышц. Мышцы никогда не работают в одиночку – каждое движение есть результат действия взаимно противоположных мышц – антагонистов. При каждом сгибании действует не только сгибатель, но обязательно сокращается разгибатель, постепенно уступая сгибателю и удерживая его от чрезмерного сокращения. Антагонизм мышц обеспечивает плавность и соразмерность движений. В отличие от мышц – антагонистов мышцы, равнодействующая которых проходит в одном направлении, называются синергистами. В зависимости от характера движения и комбинации мышц, участвующих в нем, одни и те же мышцы могут выступать как синергисты, так и как антагонисты [1].

Необходимо отметить, что положение головы в пространстве и диапазоны движений обусловлены не только степенями свободы атланто-затылочного и атланто-осевого суставов, но и подвижностью шейного отдела позвоночного столба.

Сгибание и разгибание головы в атланто-затылочном суставе в сагиттальной плоскости возможны в пределах: 300 – вверх, 200 – вниз. Наклоны головы в стороны – в пределах ±150 . Вращение в ность шейного отдела позвоночного столба расширяет диапазон поворота головы вокруг вертикальной оси до ±700 , а в сагиттальной плоскости – вверх до 400 , вниз – до 300 [2].

атланто-осевом суставе вокруг вертикальной оси – в пределах ±350 . Подвиж-

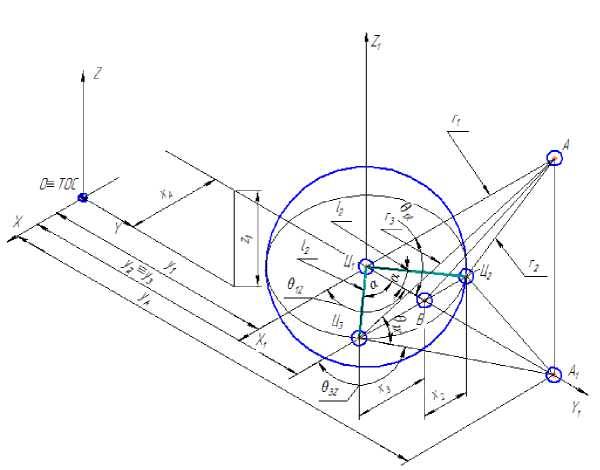
Рисунок 1 – Базисная модель зрительного анализатора

Наличие двух суставов и гибкость шеи дают возможность голове совершать не только вращательные, но и возвратнопоступательные движения. При этом траектории движений точек, лежащих на поверхности головы, могут принимать вид сложных пространственных кривых.

При этом следует иметь в виду подвижность зрительного анализатора (глазных яблок), нижний предел которого – 65÷750 , а верхний – 50 ÷ 600 . Зрительный предел бинокулярного зрения в горизонтальной плоскости составляет 1240 .

При решении эрготехнических и кибернетических задач требуется производить обработку информации о движениях частей тела человека-оператора. Движение любого тела – это изменение координат его положения в течение времени.

Существует много систем координат для определения места точки или твердого тела в пространстве. Нас интересует преобразование координат положения глаз и головы, которые могут двигаться в трёхмерном евклидовом пространстве. В этом случае для аналитического выражения необходимых связей удобнее принять в качестве опорной трёхмерную декартовую систему.

Будем считать, что система OXYZ– неподвижнаясистема координат, связанная с сиденьем оператора, будет являться основной (рис. 1). Понятно, что это грубое условие, поскольку сиденье участвует в сложном движении: оно двигается поступательно или вращается вместе со строительной машиной (к примеру, при повороте платформы башенного крана), кроме того, участвует в поступательном движении за счёт передающихся на него через металлические конструкции кабины вибрационных воздействий от двигателя или трансмиссии.

Вторая система координат Ц1X1Y1Z1 – неизменножестко связана с головой оператора (угловая система координат). Начало системы угловых координат находится в центре движений головы Ц1 и соответствует полюсу её движений. Будем считать, что ось головы вертикальна и проходит через Ц1. Система координат O1X1Y1Z1 имеет начало координат в точке О1, совпадающее с началом системы угловых координат, но может поворачиваться вокруг этой точки относительно головы, неизменно сохраняя параллельность своих осей одноименным осям системы основных координат. При таком выборе декартовых си- стем координат описание движения головы сводится к описанию перемещения систем угловых и поступательных координат, то есть к определению положения этих систем в основной системе координат в произвольные моменты времени [1,3].

От системы угловых координат Ц 1 X 1 Y 1 Z 1 можно перейти к системе поступательных координат и обратно путём трёх последовательных поворотов осей первой системы на углы Эйлера [1,4]. При перемещении системы Ц 1 X 1 Y 1 Z 1 на углы Эйлера голова совершает повороты вокруг осей O¹X¹, O¹Y¹, O¹Z¹ на углы θ 1x , θ 1y , θ 1z соответственно. Угол поворота θ 1x головы вокруг оси O¹X¹– уголкивка. При совершении кивка голова движется в медианной (или сагиттальной) плоскости S , являющейся вертикальной плоскостью симметрии головы. В сагиттальной плоскости лежат сагиттальная O¹Y¹ и вертикальная O¹Z¹ оси системы поступательных координат O¹X¹Y¹Z¹. Угол θ 1y служит для оценки величины поворота головы вокруг сагиттальной оси и называется углом наклона. Если угол θ 1y ≠0 , то голова совершила угловое перемещение во фронтальной плоскости p 2 , перпендикулярной к медианной (сагиттальной) плоскости и проходящей через латеральную O¹X¹ и вертикальную O¹Z¹ оси системы O¹X¹Y¹Z¹ . Такие наклоны головы оператор выполняет крайне редко, а поэтому в дальнейшем при программировании пространственного движения зрительного аппарата мы их не будем рассматривать. Поворот головы вокруг вертикальной оси совершается в венечной (горизонтальной) плоскости p 1 . Угол поворота вокруг оси O¹Z¹ обозначен через θ 1z . Медианная, фронтальная и венечная плоскости пересекаются, образуя координатные оси O¹X¹, O¹Y¹, O¹Z¹, которые в свою очередь пересекаются в полюсе движения головы (в точке O¹).

Углы θ 1 x , θ 1 y , θ 1 z однозначно определяются направлениями осей системы угловых координат O 1 X 1 Y 1 Z 1 . По ним можно судить о том, как ориентирована голова в соответствующие моменты времени, поэтому величины θ 1 x , θ 1 y , θ 1 z называют угловыми координатами или координатами ориентации головы.

Во время выполнения определенных целенаправленных движений голова может совершать сложные движения, в результате которых полюс её движений сместится из первоначального положения – точки Ц1 в новое положение – O1 . Положение точки в основной системе координат OXYZ определяется тремя линейными координатами x, y, z,которые представляют собой три линейные перемещения, параллельные латеральной O1X1, сагиттальной O1Y1 и вертикальной O1Z1 осям и при помощи которых начало системы поступательных координат О1 можно переместить из начала основной системы координат в новое положение.

Величины x, y, z , определяют место полюса движений головы и называются координатами места головы в основной системе координат или просто координатами места [1, 5, 6].

Совокупность координат ориентации и координат места определяет положение головы наблюдателя в трехмерном евклидовом пространстве и называется координатами положения [1, 5, 6].

Таким образом, положение головы наблюдателя относительно объекта наблюдения в общем случае определяется шестью координатами – тремя координатами ориентации и тремя координатами места.

Как уже было отмечено выше, зрительный аппарат человека образуют глаза и голова. Базисная модель зрительного аппарата состоит из трех твердых тел, имитирующих глаза и голову, соединенных шарнирно [3, 5]. Схема базисной модели зрительного аппарата приведена на Рисунке 1. Для упрощения чтения чертежа оси угловых и поступательных координат изображены совмещенными. В точках Ц2, Ц3 находятся центры движения глаз, через которые проходят зрительные оси и неподвижны относительно головы. Точка фиксации взглядаА обозначает наблюдаемый человеком-оператором объект, относительно которого осуществляется ориентация всего поля зрения. Прямая, соединяющая точки Ц2и Ц3 называется базовой линией [5, 6]. ТочкаВ, лежащая на её середине, называется циклопическим глазом. Вектор, начало которого совпадает с циклопическим глазом, а конец – с точкой фиксации, изображает направление взора наблюдателя. Прямые Ц2А и Ц3А являются зрительными осями левого и право- го глаз соответственно. Эти оси пересекаются в точке фиксации взора. Ориентация зрительных осей определяется углами между зрительной осью и прямой, параллельной вектору направления взора и проходящей через центр движения глаза: θ2x ,θ2z ,θ3x ,θ3z, причем индексы: «2» – для левого глаза, «3»  – для правого;

«θ 2 z » ( « θ 3 z ») - углы поворота глаз в горизонтальной плоскости, «θ 2 x θ 3 x » – всагит-тальной плоскости (рис. 1).

Такая модель, имитирует зрительный аппарат, способный обозревать объекты, как угодно расположенные в пространстве, но лишь в пределах возможных поворотов глаз и головы.

Треугольник зрительного аппарата Ц 1 Ц 2 Ц 3 образован прямыми равными, l 2 , а угол между ними равен 2α . Значения расстояния между зрачками b , а также l 2 и α приняты в соответствии с известными максимальными, минимальными и средними антропометрическими данными [2] (Таблица 2).

Точка Ц1может оставаться неподвижной, и тогда ее координаты места будут представлены как постоянные величины, а может двигаться, и в этом случае они будут заданы как функции времени. На движение точки Ц1наложены три связи. Движение точек Ц2и Ц3 связано с движением головы, и это дает дополнительно 6 связей. Все девять уравнений связей могут быть представлены системой уравнений (1). Нижеприведенная система уравнений связей (1) составлена для общего случая. В выбранной же нами системе координат сагиттальная O1Y1 и латеральная O1X1 оси являются осями симметрии головы, пересечение которых есть центр головы Ц1. Прямая Ц1В проходит через циклопический глазВ, а поэтому x1=y1=0. Кроме того, уравнения координат для центров глаз Ц2, Ц3 составлены с учетом возможного вращения головы вправо, то есть для правой систе x1 = x1 (t )[Л1 = const];

У 1 =У 1 ( t )[ 6 2 = const ];

z 1 = z 1 ( t )[ 6 ₃ = const ];

x2 ⁼ x 1 + l 2 sin(0 1 _z - a);

* У 2 = У 1 +l 2 cos(0 1 z- a);     (1)

^z 2 =^z i ;

x ₃ = x 1 + l ₂ sin(0 1 _z + a);

У 3 = У 1 + l 2 cos(0 1 z + a);

[^z 3 = ^z -

В целом система принятой модели зрительного аппарата имеет 16 степеней свободы. Считая, что наклоны головы в стороны оператор выполняет крайне редко, исключаем угловую координату θ1y, а значит, условно освобождаемся от одной связи в виде угловой координаты. После наложения 9-ти связей (1) базисная модель будет иметь 6 степеней свободы, и её конфигурация определяется шестью углами, следовательно, полная программа должна иметь 6 уравнений.

Определим, какими могут быть уравнения, представляющие программу пространственного движения зрительного аппарата при выполнении оператором строительной (в частности, подъемнотранспортной) машины целенаправленной деятельности.

Пусть зрительный аппарат оператора фиксирует или сопровождает наблюдаемый объект, обозначенный точкой А (рис. 1). Тогда программа движения глаз должна состоять в том, чтобы зрительные оси обоих глаз проходили через одну и ту же точку А . При условии плавного слежения программа может быть представлена следующими выражениями [3, 5, 6]:

tg _{2 z}

tg _{3 z}

tg _{2 x}

x_A  x ₂

y_A  y ₂

^XA-^X 3 _;

y_A  y ₃

z_A z ₂

4 ( xA	X 2  . Z              x2 ; x 2 )  "*"( y A    y 2 )
	zA  z 3

t^ 3 x= ,,-----------. --------------7-

_        \/^{( X}A^-x 3 ) ⁺⁽ Ул^—У 3 )

Эту программу можно переписать иначе [5]:

( XA-X ₂ )cos0 _{2 z} +( У A-У ₂ )sin0 _{2 z} =0;

( xA -x 3 )cos 3 z + ( у A - у 3 )sin0 3 z =0;

- X2 )cos02 rr^ sin©2=0;

^{( X}A

cos©2+ r^ sin02_x = 0;

(XA -x3)cos©3Х + Гз sin0^x =0, где

r ₃

^r 2= 4 ⁽ xA-x 2 ) ² +⁽ Ул-У 2 ) ²   ,

/(xA-x3)2 +(Ул-У3)2  - значения рас- стояний от центров глазных яблок до наблюдаемого объекта.

Программа представлена 4-мя уравнениями, и может быть дополнена уравнениями координат наблюдаемых объектов. Координаты наблюдаемых объектов в зависимости от характера за- дачи могут быть определены различными выражениями. Мы рассмотрим в качестве объекта наблюдения груз на крюке (или крюк) на канате строительного крана. Такой выбор неслучаен, поскольку этот объект наблюдения среди прочих (члены бригады, стропальщики, места складирования, автомашины и др.) является особо опасным. От того, насколько доступен этот объект для наблюдения за ним, зависит безопасность проведения работ на строительной площадке, так как операто- ру строительного крана важно видеть, как закреплён груз, как осуществляется его подъём или спуск, в каком состоянии готовности место его посадки и т.п.

Координаты точки, имитирующей груз на канате строительного крана, должны быть заданы как функции времени, при этом значения координат будут зависеть от характера движения крана, тележки, грузового каната и т.д.

Если, к примеру, груз закреплен на крюке грузового подвеса строительного крана, совершающего поворот относительно вертикальной оси на угол φ , то программа движения зрительного аппарата может быть дополнена следующими уравнениями:

Хд = -[ R^a ^ ( t ) L ]sincp( t ) + ot^( t ) L coscp( t ); y^ = [ R + oc ^( t ) L ]coscp( t ) + oc^( t ) L sincp( t );

z д =-L cosoi^( t )cosoc^( t), где:R – длина стрелы крана, м; L– длина троса, м; φ – угол поворота крана, рад; αТ , αR– углы отклонения груза в радиальном и тангенциальном направлениях, рад. Углы отклонения груза и поворота крана могут быть заданы некоторыми постоянными значениями или как функции времени.

В случае задания координат груза на канате строительного крана, совершающего поворот, как функций времени, речь может идти о программе движения зрительного аппарата за областью или зоной. При постоянных значениях углов φ, α Т ,α R можно говорить о программе слежения за объектом.

Если решается задача о наблюдении за перемещением груза при подъеме и опускании грузового подвеса строи- тельного крана, то координаты груза или грузового крюка могут быть определены уравнениями поступательного движения тела:

xA =/ 1 ( t );

yA ~^ 2⁽ t ^);

^zA ^=f 3⁽ t )•

При этом в частном случае можно принять постоянными значения координат x и y , поскольку опускание и подъем как груза, так и грузового крюка производится при остановке крана. Предполагая, что груз перемещается равномерно, то есть модуль скорости не меняется, уравнения координат наблюдаемого объекта примут вид:

x const;

Уа = const,- ;

dS z j z          t.

A 0 _dt

При равноускоренном движении груза его координаты будут определены системой уравнений:

x    const;(7)

y    const;

~~ zA z0 V0t где ~ = dV,  ~ = dS.

dt

При известных границах наблюдаемой зоны (рис. 2) можно написать программу слежения аналогичную программе слежения за объектом (8).

При решении конкретной задачи программа может быть дополнена уравнениями координат наблюдаемых объектов.

Программирование движения зрительного аппарата оператора строительной машины (крана) при выполнении целенаправленного действия – наблюдения за объектами может быть упрощено за счёт применения циклопического глаза. Решение задачи, таким образом, сводится к определению фактических значений отклонения зрительной оси, проходящей через циклопический глаз (В) и наблюда- емый объект (А), в вертикальной (θВx) и горизонтальной плоскостях (θВz) и сравнению их с физиологически допустимыми (рис. 1, 2).

уравнениями координат наблюдаемого объекта.

При этом координаты циклопического глаза, общем виде, определяются системой уравнений:

tg _{3 x}

z_A z ₃

tg _{3 x}

D         x 2 . z          2Г ^;

\)^{( x}A- x 3 ) ⁺⁽ Уа-У 3 ) z_E  z ₃

tg _{3 x}

M^{! (} X£-x 3 ) ² +⁽ Уе-У ) ²

z_F  z ₃

Г/          X 2 . z           2T ^;

\l ^{( X} f  ^x 3 ) +^{( y}F  ^y 3 )

tg _{3 x}

z_i  z ₃

I --------------------------------------------------------------------•

V⁽ x-x 3 ) 2 +( У.-У 3 ) 2

tg ₃

tg _{3 z}

xA-x 3 _;

y_A y ₃

x_E  x ₃

;

yEy

,gO3z=-xF-X3 ;

yFy

•••••••••• •••••••••• ••••••

•••••••••• •••••••••• •••••• tg9 3z=-xz3xL ;• yi  y3

tg _{2 x}

z_A z ₂

tg _{2 x}

tg _{2 x}

tg _{2 x}

tg 2 z      ^{x A   x 2} ;

y_A  y ₂

_{tg 2 z}      x E   x 2 _;

y_E  y ₂

_{tg 2 z}      x F   x 2 _;

y_F  y ₂

xx tg 2z       i 2 ;

y_i   y ₂

'4^{1 (} x A -x 2 ) ² +( Уа-У 2 ) ²

z_E z ₂

Л /⁽ x E   x 2 )  "*" ⁽ y E y 2 )

z_F z ₂

2                         ^;

J ^{( X} f x 2 )  "*"⁽ y F y 2 )

z_i   z ₂

V⁽ x.-x 2 )^{2 +(} У^У 2 )²

•

Программа движения циклопического глаза представляет систему уравнений [5]:

xx g bz=-;

yA  yВ zA  zВ

^tg6ВХ^- .Г,       "T-y        TT^;

■\l ⁽ x A -x B ) +⁽ Уа-У в )

^ ( BA)=yj( Xa-X b ) 2 +( У а -У в ) 2 +( ^ a" z в ) 2 •

Поскольку программа не полна, то ее можно дополнить уже известными

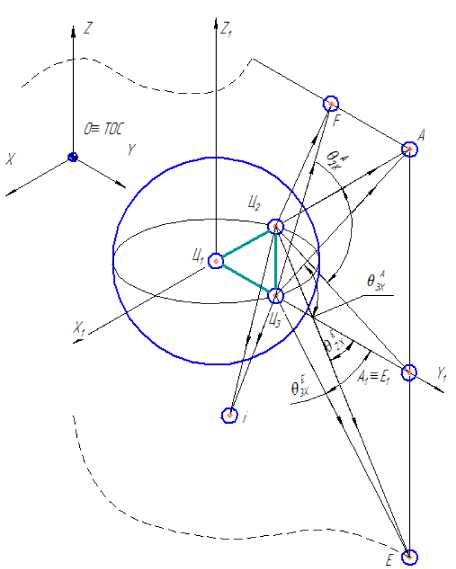
Рисунок 2 – Схема для программирования движения зрительного аппарата оператора при наблюдении за зоной обзора

x _B x ₁ l ₂ cos sin _{1 z} ;

y _B y ₁ l ₂ cos cos _{1 z} ; (10)

z _B z ₁ .

Задача по исследованию возможностей получения визуальной информации оператором строительной машины посредством глаз и головы решалась в следующей последовательности:

• 1.    По известным координатам наблюдаемых объектов или области наблюдения и координатам места центров головы и глазных яблок определить фактические значения координат ориентации (угловых координат) глаз;

• 2.    Сравнить полученные значения координат ориентации (угловых координат) глаз с физиологически возможными;

• 3.    Дать рекомендации по совершенствованию поста управления и обзорных качеств кабины с целью удобства получения оператором визуальной информации при минимальных энергетических затратах.

Рассмотрим задачу при известных исходных значениях (Таблицы 2, 3), проиллюстрированную на Рисунке 3.

Обеспечение визуального комфорта оператора достигается в том случае, когда наблюдаемый объект фиксируется в пределах бинокулярного поля зрения, границы которого определяются физиологией человека.

Пространственное положение глаз оператора, находящегося в физиологически рациональной рабочей позе (Рисунок 1), определяется в основной системе OXYZ , начало координат которой О совпадает с точкой отсчёта сиденья (ТОС). Антропометрические размеры l, h, b, а , h 2 , l 2 остаются неизменными для выбранных роста и позы оператора (Таблица 2) [2]:

Таблица 3 –Значенияамплитуд движения

головы опе		ратора
Част ь тела	Звено	Угол поворота			Очередность поворота
		Обо-значение	Ось поворота	Значение, В градусах
Голова	АЦ 1 Ц 2(3)	θ 2x 0 2z	O/X/ O/Z/	+30, -20 +35,35	1 2

Упрощённая модель зрительного

В выбранных системах угловых и линейных координат при расположении зрительного аппарата в соответствии с рис. 3, 4 наблюдение за объектами из проектного положения осуществляется при следующих значениях линейных координат:

х 1 =0 ;

У1 = 1-1^ =1-12 cosoe;

z1 hh;

x^ = x i - к since = -Л since;

,         i               (11)

* У2= У1 ^+/ 1= У1 + /2 cosoe;      ^{v 7}

z 2 = h ;

x 3 = x i + / 2 sina ⁼ / 2 ^s in<^;

• У3 ⁼ У1 + / 2 cosoe;

• z 3 hh .

С целью увеличения зоны видимости оператор строительного крана (чаще всего башенного крана) вынужден выполнять наклоны вниз и вверх посредством головы, шеи и туловища с использованием вращательной способности глазных яблок. Составление уравнений линейных координат при изменении положения перечисленных выше органов представляет непростую задачу, поэтому остановимся на новых значениях линейных координат глазных яблок при вращении головы оператора «направо» в горизонтальной (12) и «вниз» в сагитталь- аппарата представлена в виде шарнирного соединения пары звеньев (Рисунок 3), одно из которых соответствует шее (AN), а другое - голове(АЦ1Ц2(3)). Шарнир N расположен на основании седьмого шейного позвонка, а точкаА соответствует атлантозатылочному сочленению. Опорные точки Ц3(Ц31, Ц32, Ц33) и Ц2(Ц21, Ц 22, Ц23) представляют собой центры хрусталиков правого и левого глаз человека [5,6]. Геометрические размеры l, h, b, а , h2, l2 характеризуют основное положение звеньев и соответствуют антропометрическим размерам.

ной (13) плоскостях.

• xi = х 1 = 0 ;

• У1 ⁼ У1 =^l-h = ^l~^l 2 coset;

z 1 = z1 = h ;

x 2 ⁼ x 1 ⁺ / 2 sin(0 1 z - a) = 1 ₂ sin(0 1 z - a);

< y 2 = y1 + / 1 = У1 +¹ 2 ^cos(e 1 z - ce);

z 2 = h ;

x g = x i + / 2 sin(0 1 z + ot) = / 2 sin(0 1 z + ot);

У 3 ⁼ У1 ⁺ / 2 cos(0 1 z + ot);

z 3 = h .

' 4 = 0 ;

yi⁼ y 1+ i 2™;

z1 = h-l ₂ (1- cos 01 x );

x 2 = x 1 - 1 ₂ since = - l ₂ since;

< y 2 = l 2 (sinO 1 x + ^cos 0i x );         ⁽¹³⁾

z 2 = h-l ₂ ( 1 -cos 0₁ x + sin0 ₁ x );

x 3 ⁼ x ₁ ⁺ 1 ₂ since = 1 ₂ since;

y 3 = l 2 (sinO 1 x + ^cos 01 x );

z 3 = h-l ₂ ( 1 -cos 0₁ x + sin0 ₁ x ).

Вывод значений координат глазных яблок при вращении головы проиллюстрирован на рисунке 4.

На основании приведенной выше программы был сделан анализ обзорных качеств кабин башенного, гусеничного и автомобильного строительных кранов.

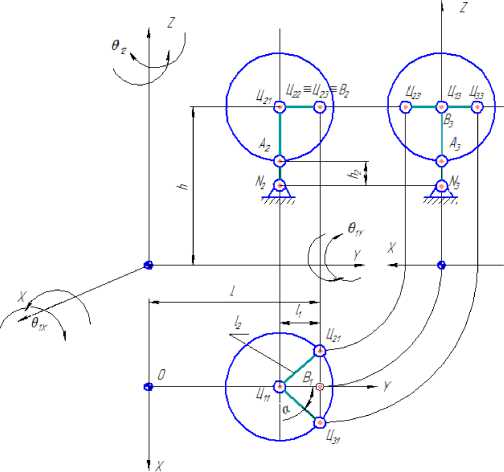
Рисунок 3 – Схема для определения координат зрительного анализатора оператора при наблюдении за объектом

В Таблице 4 приведены некоторые результаты расчетов возможных фактических углов вращения глазных яблок в горизонтальной и сагиттальной плоскостях из проектного положения оператора со средними антропометрическими данными. В качестве объектов наблюдения рассматривались как благополучные в плане доступности получения визуальной информации, так и неблагоприятные. Надо отметить ещё раз, что труднодо- ступными для осуществления процесса слежения за объектами являются объекты нижней зоны, находящиеся практически под углом 900 вниз от главной линии взора наблюдателя при их незначительном удалении от оси OY в обе стороны (к примеру, объекты, участвующие в строительно-монтажных работах нулевого цикла или первых этажей). При выполнении работ с помощью мобильных строительных машин (автокрана, гусеничного крана, экскаватора) зачастую недоступны объекты верхней зоны (навесное оборудование).

O^TOC

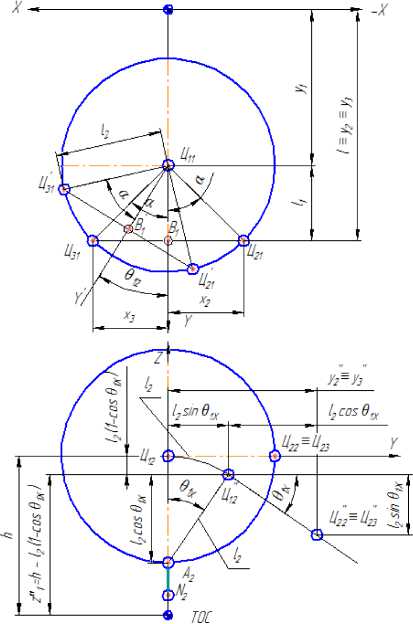
Рисунок 4 – Схема динамики зрительного анализатора

Анализ результатов выполненных расчетов с использованием математического пакета Mathcad [7], частично представленных в Таблице 4, позволяет сделать следующие выводы:

• 1.    Получение визуальной информации практически при любом расположении объектов в области передней полусферы, можно осуществлять за счёт вращения глазных яблок в пределах физиологически возможных углов в горизонтальной плоскости;

• 2.    Для получения визуальной информации в сагиттальной плоскости фи-

• зиологически возможных значений углов вращения глазных яблок недостаточно, чтобы увидеть некоторые объекты;

• 3.    Достижение цели по получению визуальной информации с вращением головы и глаз в незначительной степени увеличивает обзорность;

• 4.    При переносе уровня расположения глаз по вертикали (вверх или вниз), то есть при работе «стоя» или «согнувшись вниз» объекты становятся видны;

• 5.    Анализ по п.п. 1 – 4 даёт право, говорить о необходимости совершенствовать обзорные качества кабин за счёт проведения инженерно-технических мероприятий, связанных с разработкой и проектированием кабин с прозрачной передней полусферой и сиденья оператора, позволяющего существенно регулировать уровень расположения точки взора (линии взора) оператора (не менее 500 мм по высоте и по углу наклона сиденья в диапазоне от 12⁰ до 17⁰ – без применения мер безопасности и до 30⁰ с применением безопасных устройств, обеспечивающих устойчивое положение оператора на рабочем месте).

Таблица 4 – Результаты расчетов

Координаты возможных положений груза на грузовом подвесе			θ 2z	θ 3z	θ 2x	θ 3x
X A ,мм	Y A ,   Z A ,мм мм
Башенный кран КБ-405.1
5000	5000	-25000	450 51΄	450 08΄	740 42΄	740 54΄
5000	5000	-35000	450 51΄	450 08΄	780 54΄	790 00΄
5000	5000	-45000	450 51΄	450 08΄	810 12΄	810 18΄
10000	10000	-25000	450 26΄	450 04΄	610 16΄	610 25΄
10000	10000	-50000	450 26΄	450 04΄	740 27΄	740 33΄
5000	5000	15000	450 51΄	450 08΄	630 38΄	630 55΄
10000	10000	15000	450 26΄	450 04΄	450 14΄	450 24΄
15000	5000	10000	710 56΄	710 47΄	580 24΄	580 36΄
Гусеничный кран КС-8161
7000	6000	25000	500 00΄	490 36΄	690 12΄	690 24΄
7000	6000	36000	500 00΄	490 36΄	750 19΄	750 30΄
Автокран КС-3562А
5000	4000	10000	520 18΄	510 48΄	550 18΄	550 42΄
5000	10000	5000	270 04΄	260 30΄	200 48΄	200 54΄