Графоаналитический метод анализа мультиверсионных архитектур программного обеспечения

Компоненты программного обеспечения (ПО), обладающие свойством отказоустойчивости, уже много лет являются неотъемлемой составляющей как коммерческих, так и специальных систем управления и обработки информации. Известны различные методы проектирования отказоустойчивого программного обеспечения [1]. Хорошие перспективы в этой области имеет метод муль-тиверсионного проектирования [2].

Однако, учитывая сложность мультиверсионных систем управления и обработки информации и множество параметров системы, которые могут изменяться во времени, осуществлять прогноз времени завершения задач, и оценивать надежность системы, основываясь только на статических или детерминированных моделях систем или программ, достаточно сложно, а в некоторых случаях просто невозможно. Это обстоятельство представляется нам научной проблемой, выражающейся в необходимости поиска новых подходов к анализу надежности, а также временных характеристик работы программного обеспечения, построенного на основе мультиверсионной архитектуры.

Одним из таких подходов является графоаналитический метод, основанный на использовании GERT-сетей [3]. Основное достоинство этого подхода заключается в том, что он может быть успешно применен к решению практически любой задачи сетевого анализа и дает возможность составить формальные процедуры для определения вероятностно-временных характеристик системы.

Опишем модель мультиверсионного ПО, основанного на N -версионной архитектуре [4] (рис. 1) в виде GERT-сети (рис. 2), и рассчитаем ее основные характеристики при условии, что количество мультиверсий N = 3, а остальные параметры представлены в таблице.

Узлы стохастической сети (см. рис. 2) могут быть интерпретированы как состояния системы, а дуги – как переходы из одного состояния в другое. Такие переходы можно рассматривать как выполнение обобщенных операций, характеризуемых плотностью распределения, или функцией массы, и вероятностью выполнения [5].

Каждый внутренний узел стохастической сети выполняет две функции, одна из которых касается входа в узел, а другая – выхода. Обычно эти функции называют входной и выходной. Входная функция определяет условие, при котором узел может быть выполнен, а выходная – совокупность условий, связанных с результатом выполнения узла. Другими словами, с помощью выходной функции указывается, должны ли выполниться все операции, которым данный узел непосредственно предшествует, или только одна из них. Отметим, что начальный узел сети выполняет только выходную функцию, в то время как конечный узел – только входную.

Рис. 1. Модель N -версионного программирования

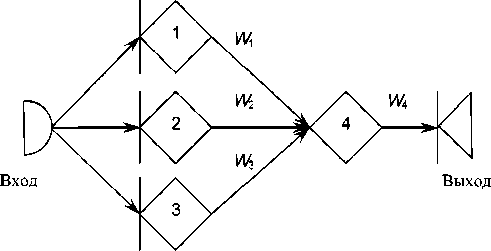
Рис. 2. Модель N -версионного программирования в виде GERT-сети

Существуют следующие виды входных функций:

– AND-функция (узел активируется, если выполнены все дуги, входящие в него);

– IOR-функция (узел активируется, если выполнена любая дуга, входящая в него);

Характеристика операций

Ветвь	Вероятность того, что операция будет выполнена pi	Тип распределения	Параметры, мс
(1, 4)	0,85	Нормальное	m = 0,5 σ = 0,1
(2, 4)	0,85	Нормальное	m = 0,5 σ = 0,1
(3, 4)	0,85	Нормальное	m = 0,5 σ = 0,1
(4, выход)	0,99	Нормальное	m = 2 σ = 0,5

– EOR-функция (узел активируется, если выполнена любая дуга, входящая в него, при условии, что в данный момент времени может выполняться только одна дуга, входящая в данный узел).

Используются следующие виды выходных функций:

– детерминированная функция (все дуги, выходящие из узла, выполняются, если узел активирован);

– стохастическая функция (только одна дуга, выходящая из узла, выполняется с заданной вероятностью, если узел активирован).

Комбинируя все входные и выходные функции (рис. 3), получаем шесть различных типов узлов. Активация узла означает, что система перешла в некоторое состояние, и определяет множество возможных дальнейших действий. Одно или несколько действий начинают свое выполнение сразу после активации узла, являющегося их началом. Активация узла происходит, если его входная функция выполнена. После выполнения выходной функции активированного узла, т. е. начала выполнения соответствующей дуги, он становится неактивным [3].

к < с

EOR-вход          IOR-вход          AND-вход

Стохастический выход           Детерминированный выход

Рис. 3. Графическое обозначение входных и выходных функций GERT-сети

Необходимым и достаточным условием функционирования мультиверсионного модуля ПО является выполнение хотя бы одной мультиверсии. Поэтому узел 4 на рис. 2 является узлом с IOR-входом. Выбор данного типа узла основан на том, что этот узел активируется при выполнении любой дуги, входящей в него.

Рассмотрим методику расчета сети, содержащей IOR-вход и детерминированный выход (рис. 4) и состоящей из нескольких подсетей (рис. 5).

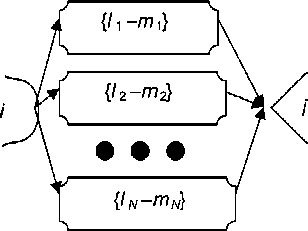
Рис. 4. IOR-вход: j – вычисляемый IOR-вход, имеющий стохастическое начало в узле i ; { l ₁ – m ₁}, { l ₂ – m ₂}, …, { l_N – m_N } – N непересекающихся подсетей

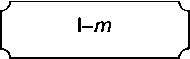
Рис. 5. Произвольная подсеть с начальным узлом l и конечным узлом m

Пусть p_ij – вероятность того, что операция ( i , j ) будет вы-полнена при условии, что узел i выполнен. Тогда по представленной выше таблице имеем:

P j = Pi [1 — (1 — Pl 1, m 1 k ) ^{x x (1} - pl 2, m 2 k )...⁽¹ - ^P N , m N k )]•

Учитывая, что от входа до узла 4 находится три непе-ресекающиеся подсети, используя выражение (1), в данном частном случае получим

P4 = Pвх [1 — (1 — P1)(1 — P2)(1 — P3)] =

= 1 - ( 1 - 0,85 ) 3 = 0,996 625.

Воспользовавшись правилом Мейсона для замкнутых потоковых графов, выведем эквивалентную W -функцию [5] для этой сети:

W e ( 5 ) = W ^ ( 5 ) ■ W 4 ( 5 ) =

0,5 5 + 2o,1² ■ 5 ²             2 5 + io,5² ■ 5 ²

= 0,996 6 e    ²      ■ 0,99 e ¹

= 0,986 6 e ^{215 5 + 0}-^{13 5} .

Легко проверить, что для рассматриваемой задачи WE (0) = 0,986 6. Данную величину можно интерпретировать как вероятность безотказной работы мультивер-сионного ПО. В свою очередь математическое ожидание времени выполнения сети составит af We (5) 1

d M ( 5 )        I W e (0) ^J

Ц1E = —;--- =----;---- = 2,5 мс, a5 5=0

5=0 а дисперсия будет d2M(55)_

^1E = ——   = 6,51 мс2.

Следует заметить, что при расчете сети, содержащей IOR-вход и детерминированный выход, если все подсети представляют собой мультиверсионный модули с одинаковой надежностью, то формула (1) может быть сведена к виду

P j = P i -[1 — (1 — P 1, m ) n ]• (6)

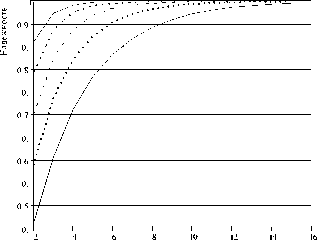
Графическая зависимость между числом мультивер-сионных модулей и надежностью системы приведена ниже (рис. 6). На оси Х обозначено количество мультиверсий, на оси Y – надежность системы для разного количества модулей с разной надежностью каждого модуля (от 30 до 80 %).

Количество модулей

30            60

40            70

50            80

Рис. 6. Зависимость между числом мультиверсионных модулей и надежностью системы

Таким образом, использование графоаналитического метода на основе GERT-сетей для анализа мультивер-сионных архитектур программного обеспечения является перспективным, так как позволяет аналитически оценить вероятностно-временные характеристики мульти-версионного ПО любой сложности без построения громоздких имитационных сред и комплексов моделирующих программ.