Графоаналитический метод расчета конвективно-терморадиационной сушки технических тканей

В настоящее время широко применяются декоративные многослойные материалы с использованием технических тканей, которые после специальной технологической обработки подвергаются сушке. Такие декоративные ткани используются в обувной промышленности, при производстве высококачественных обоев, при создании декоративно-отделочных покрытий в строительстве.

Ткани проходят технологическую обработку специальными полимерными аппретами и клеевыми пропитками для обеспечения жесткости и каркасности. Нанесение аппрета на ткань с одновременным увлажнением производится в плюсовочных ваннах, затем ткани подвергаются каландрированию для обеспечения равномерной влажности.

Сушка тканей термоизлучением относится к одним из перспективных методов термиче-ско-го обезвоживания материалов. Эффективность конвективно-терморадиационной сушки заключается в значительной интенсификации процесса влагообмена, обеспечивает высоко-темпе- ратурный нагрев ткани, уменьшает миграцию красителей и аппретов и создает высо-кую интенсивность испарения влаги с поверхности материала за счет максимальной глубины проникновения инфракрасных лучей в ткань [1].

Графические методы широко используются при расчетах нагрева и охлаждения твердых тел, в процессах сушки зернистых и сыпучих материалов, в пневматических трубах-сушилках, в сушилках с кипящим слоем, аэрофонтанных сушилках. Расчеты по графикам и номограммам значительно сокращают время, трудоемкость и объем расчетной работы. Графики и номограммы строятся на основе обширного числа экспериментальных исследований и требуют достоверных данных по тепломассообменным и теплофизическим характеристи-кам различных материалов. Теплофизические характеристики тканей хорошо изучены и даны в таблице 1 [2].

ПОСТАНОВКА ЗАДАЧИ

Сушка тканей проводилась на металлической поверхности стола экспериментальной установки в условиях вынужденного теплообмена. Ткань

Таблица 1 – Зависимость коэффициента температуропроводности для тканей от влажности
Вискоза Л = 0,058 Вт/ м • °С ; с0 = 1600 Дж/ кг • °С					Лен Л = 0,046 Вт/ м • °С ; с0 = 1500 Дж / кг • °С
W , %	λ , Вт / м · ºС	ρ , кг / м3	с , Дж / кг · ºС	а • 104, м2 / ч	W , %	λ , Вт / м · ºС	ρ , кг / м3	с , Дж / кг · ºС	а • 104, м2 / ч
90	0,187	759	2825	3,14	160	0,276	675	3150	4,67
80	0,173	713	2750	3,17	140	0,248	637	3060	4,58
60	0,144	640	2569	3,15	120	0,219	587	2960	4,537
50	0,13	600	2462	3,16	100	0,9	537	2840	4,49
40	0,116	556	2339	3,24	80	0,161	482	2690	4,48
20	0,087	488	2031	3,16	60	0,132	430	2500	4,47
10	0,072	453	1835	3,11	40	0,104	374	2260	4,1
					20	0,075	321	1946	4,32
					10	0,06	294	1744	4,27

располагалась параллельно близко расположенным (250 мм) излучающим светлым источникам излучения. В качестве излучателей использовались лампы с нихромовой спиралью со степенью черноты окисленного нихрома е ® 0,75 - 0,8 и стекла е ® 0,85 - 0,9 . При принятом расположении ткани от излучателей угловые коэффициенты излучения, определяющие эффективность поверхности излучения, φ = 1. Степень черноты тканей е ® 0,75 - 0,85 . Исследование комбинированной сушки тканей проводилось с трехкратной повторяемостью эксперимента для каждого режима сушки для избежания ошибок и случайных результатов.

Сушка тканей проводилась при трех режимах при скорости воздуха v ® 0,8 - 1,1 м/с:

• 1.    t c = 80 ° C; t_um = 150 ° C;

• 2.    t_c = ioo ° с; “С = 190 ° с;

• 3.    t_c = 120 ° C; t_мё = 250 ° C.

2. t c = 100 ° C; “С = 190 ° C; 3. t_c = 120 ° C; t_um = 250 ° C; 5. t_c = 120 ° C; t “ _з ё = 250 ° C

На рисунке 1 представлены крив ы е сушки W = f ( τ ) и температурные кривые t = f ( τ ) при комбинированной сушке тканей из вискозы и льна для указанных режимов сушки. Видно, что сушка тканей протекает в периоде убывающей скорости как по влагосодержаниям, так и по температурам с кратковременным периодом прогрева тканей до t ~ 30 - 35 ° C за 10 - 15 с.

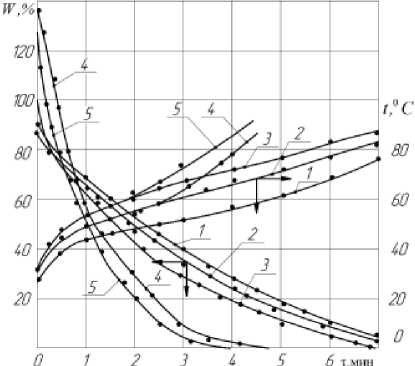
Рисунок 1 - Кривые сушки и температурные кривые для процесса сушки вискозной и льняной тканей при режимах сушки.

Вискоза: 1. t c = 80^OC; t_uЗё = 150^OC;

Лён: 4. t_c = 100°C; tT^, = 190°C;

Терморадиационная конвективная сушка тканей при принятом способе расположения материала на металлической поверхности за счет максимальной глубины проникновения излучения в ткань представляет крайне сложный процесс с переменной температурой на металлической поверхности стола, что вызывает дополнительный процесс кондуктивной сушки. Установлено [1], что влажность материала снижает глубину проникновения лучей только в периоде постоянной скорости сушки, когда поглощение излучения происходит с поверхности материала. Для тонких тканей с толщиной 6 = 0,8 - 1,2 мм в результате проникновения излучения в ткань градиенты температуры и вла-госодержания совпадают по направлению, что значительно интенсифицирует процесс влагооб-мена [1].

Примечание: λ₀ — теплопроводность сухой ткани; c₀ , c — теплоемкости сухой и влажной ткани; ρ — плотность влажной ткани; a — коэффициент температуропроводности.

Механизм такой комбинированной сушки материалов - сложный процесс тепломассообмена и строгая математическая постановка задачи на нахождение полей влагосодержаний и температуры на основе решения дифференциальных уравнений влаготеплопереноса - представляет большие трудности [1, 3, 4]. Поэтому задачу исследования комбинированной сушки тканей ограничиваем только исследованием внешнего механизма процесса сушки на основе обработки и анализа экспериментальных данных методом теории регулярного режима и обобщенных параметров процесса.

ОБРАБОТКА ЭКСПЕРИМЕНТА И ВЫВОД РАСЧЕТНЫХ УРАВНЕНИЙ

Практикой сушки установлено, что интенсивность испарения влаги, плотность тепловых потоков и среднеинтегральные температуры влажного тела в периоде убывающей скорости сушки изменяются по экспоненциальным зависимостям. А. В. Лыков [3, 4] считает, что нагрев влажного тела при условии tc = const в процессах сушки представляет собой регулярный режим, поскольку кривые сушки, температурные кривые и тепловые потоки являются экспонентами [4, 5]. В стадии регулярного режима изменение температуры и влагосодержания выражаются линей- ными соотношениями вида ln (tc - t) = f (τ) и ln(W0 - W)= f (τ) . Основным признаком регулярного режима для изменения температуры и влагосодержания являются соотношения

<6      ,    - ; dT (1) , dT                   ’ (2) где dt / dτ и dW / dτ— скорости изменения тем- пературы и влагосодержания во времени; mt и mè — темп нагревания влажного тела и темп убыли влагосодержания, мин -1; tc и t — температура среды (теплоносителя) и среднеинтегральная температура материала; W0 и W — начальное и текущее влагосодержание, %; τ — время сушки, мин.

Темп нагревания влажного тела mt и темп удаления влаги mt находятся экспериментально из соотношений [3 — 5]

Отсчетом температуры влажной ткани для всех режимов принята температура t0 ≈ 30°С от стадии прогрева тканей при τ = 10 - 15 с.

Из решения уравнений (1) — (4) находится время сушки тканей [5]:

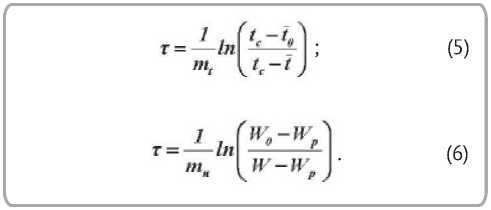
Решением уравнения (5) определяется средняя температура тканей в процессе сушки [5]

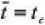
ехр(т.т)

В результате обработки опытных данных методом наименьших квадратов найдены значения m_t и m_è для тканей.

Величина темпа нагревания влажного тела m_t в условиях регулярного режима является постоянной для среднеинтегральных значений температуры и не зависит ни от режима сушки, ни от начального влагосодержания для тела заданной формы.

Темп убыли влагосодержания m_è является сложной функцией режима сушки и начального влагосодержания W₀. Режим сушки зависит от режимных параметров процесса, способа подвода теплоты, начального влагосодержания материала W₀ и прочих факторов, влияющих на процесс. Следовательно, отношение максимальной скорости сушки N_max = (dW / dτ)_max к начальному влагосодержанию W₀ можно считать обобщенной переменной, учитывающей влияние всех факторов, воздействующих на процесс сушки.

Обработкой экспериментальных кривых сушки при начальных влагосодержаниях W₀ 85, 93, 100, 120, 130, 137 % и зависимости (4) установлены соотношения, отражающие влияние и связь темпа убыли влагосодержания m_è от режима сушки и начального влагосодержания W₀: /--------------------------------------------------------------------------------------------------------'

mii = ^=87.U)-3N^ 0

или

.            (8)

I_____________________________________________________________________________________________________________________________________________________________!

Значение темпа нагревания влажных тканей m_t , вычисленное по зависимости (3) и опытных данных, приведенных на рисунке 2, оказалось равным m_t ≈ 0,24 мин^-1 .

При решении задач по нагреванию твердых тел, решении дифференциальных уравнений теплообмена, теории регулярного режима, температура задается в безразмерной форме в виде соотношения [3, 4]

.                            (9)

На рисунке 2 дана зависимость lg 0 = f (т )

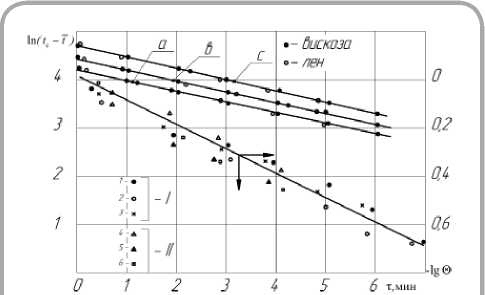
Рисунок 2 – Зависимости ln(t_c - t) = f ( τ ) Ig 0 = f ( т ) для процесса сушки вискозной льняной тканей при различных режимах. I и II:

1. t_c = 80°C; t_èçë = 150°C;

2. t_c = 100 ° C; t_èçë = 190 ° C;

3. t_c = 120 ° C; t_èçë = 250 ° C;

а . t c = 80°C; t^ = 150°C;

6. tc = 100 °C; t^ = 190°C с. tc = 120°C; t“зё = 250°C

и

и

для процесса сушки вискозной и льняной тканей. Обработка этой зависимости дала выражение

.           (10)

дуемых тканей в диапазоне влагосодержаний W₀ ≈ 90 – 137 % при равновесном влагосодер-жании W_p = 0.

Все опытные точки удовлетворительно ложатся на одну кривую для всех режимов сушки. В результате обработки эксперимента получено уравнение

,              (11)

где темп убыли влагосодержания m_è находится по выражениям (8).

Из уравнения (11) находится время сушки от начального влагосодержания W₀ до равновесного W_ð ≈ 0.

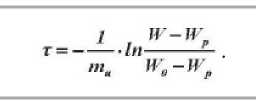
Температурные кривые для процесса сушки тканей (рисунок 1) при построении в координатах t = f (m_t · τ ) представляют прямые, выражаемые простыми линейными зависимостями, изображенными на рисунке 4. Для расчета среднеинтегральной температуры получено уравне-

Значение темпа нагревания m_t при обработке эксперимента по зависимости (3) m_t = 0,24 совпадает со значением коэффициента в уравнении (10), что подтверждает равенство темпа нагревания m_t для вискозной и льняной тканей.

Для практики сушки представляет значительный интерес обработка экспериментальных данных в обобщенных переменных, позволяющих, независимо от режима сушки, выявлять наиболее общие закономерности кинетики сушки и значительно сокращать число трудоемких и сложных экспериментов. На основе зависимости (8) и произведения m_è · τ можно построить обобщенную кривую сушки, аналогичную обобщенной кривой сушки Ф. К. Филоненко в координатах W - W_p = f (N · τ ) , где W_p — равновесное влагосодержание; N — скорость сушки в первом периоде, и на основе обобщенных переменных процесса проводить графический расчет основных параметров кинетики сушки влажных тканей.

На рисунке 3 б дана зависимость W_p = f (m_è · τ ) для процесса сушки иссле-

ние

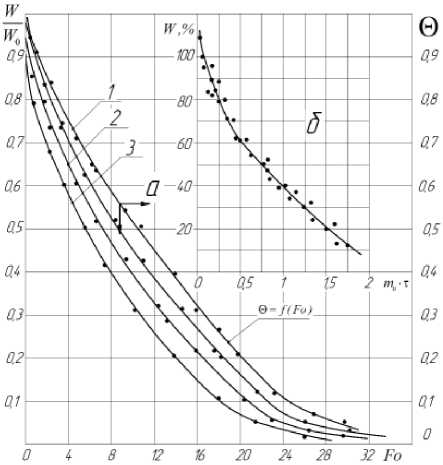
Рисунок 3 – Обобщенные зависимости

W / W o = f (Fo) ; 0 = f (Fo) и W = f (m . • т ) для процесса сушки вискозной и льняной тканей при режимах, указанных на рисунке 2

.              (13)

Рассмотрим два варианта построения графиков для расчета основных параметров кинетики сушки тканей.

На рисунке 5 а представлены зависимости © = f ( т ) и обобщенные кривые сушки W / W₀ = f ( τ ) для процесса сушки тканей.

Графический расчет кинетики сушки тканей проводится по заданному текущему значению W . Находится время сушки, относительная © и средняя температура t в процессе. По второму варианту строятся зависимости W/W₀ = f (Fo) и © = f (Fo) для каждого режима сушки тканей, где критерий Фурье Fo = à τ / R_v² ; à — коэффициент температуропроводности; R_v — характерный размер влажного материала, равный толщине ткани δ .

На рисунке 3 а изображены зависимости W/W₀ = f (Fo) и © = f (Fo) для процесса сушки тканей для заданных режимов. Графический расчет по рисунку 3 а проводится в такой же последовательности, как и по рисунку 5 а с опре-

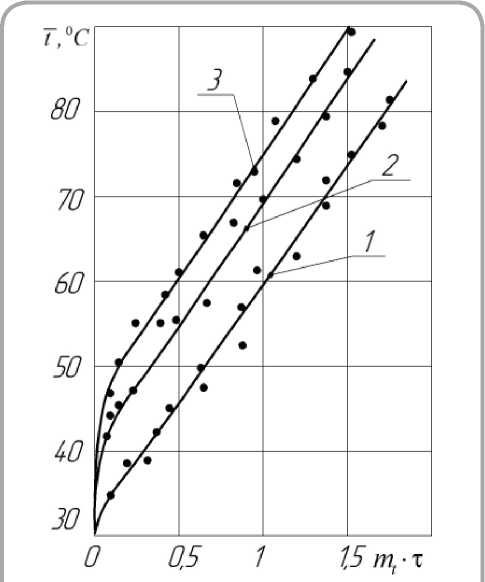
Рисунок 4 – Зависимости среднеинтегральной температуры t = f ( m_t · τ ) для процесса сушки тканей при режимах, указанных на рисунке 1

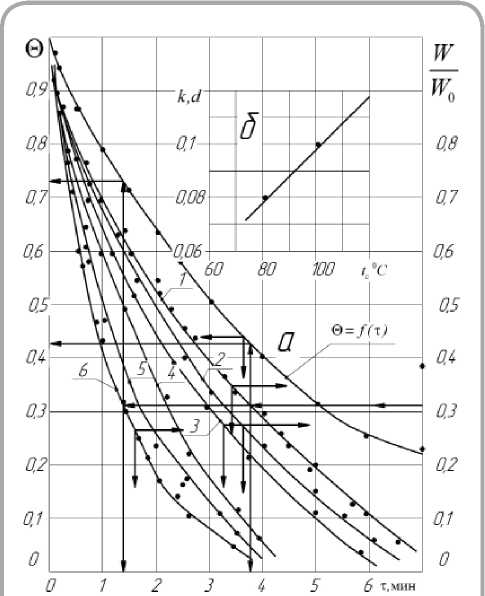
Рисунок 5 – Рисунок 5 (а, б) — Обобщенные кривые сушки W / W₀ = f ( τ ) и температурная кривая © = f ( т ) для процесса сушки тканей и зависимость постоянных k , d от температуры среды t_c . (Режимы указаны на рисунке 2)

делением времени сушки τ по критерию Фурье Fo , относительной © и средней температуры t в процессе по значениям W/W₀ = f (Fo) . Анализ данных таблицы 1 показал, что при заданном характерном размере R_v = δ ≈ 0,8 – 1,2 мм для тканей величина комплекса à / R_v² в критерии Fo принимает вполне определенные значения: для вискозной ткани à / R_v² ≈ 0,06, для льняной à / R_v² ≈ 0,16 и критерий Фурье соответственно принимает значения Fo ≈ 0,06 τ и Fo ≈ 0,16 τ , где время τ в секундах, а графический расчет кинетики сушки упрощается.

Обработкой эксперимента для процесса сушки тканей методом наименьших квадратов получены расчетные уравнения

, у (14) , (15) где значения коэффициентов к и d совпадают и находятся по зависимости [к], d = 140-3 tc.

Закономерности изменения коэффициентов к и d в уравнениях (14) и (15) даны на рисунке 5 б.

При графическом расчете кинетики сушки тканей по рисунку 3 а длительность сушки вискозной ткани находится как т = Fo / 0,06, льняной т = Fo / 0,16, где время т в секундах.

Для более полного описания кинетики сушки влажных материалов необходимо знать закономерности изменения тепловых потоков q как функцию q = f ( т , W) .

Для избежания ошибок и неточностей при обработке эксперимента вычисление тепловых потоков производилось по двум независимым формулам.

Тепловые потоки в процессе сушки определялись по уравнению теплообмена

,                (16)

где « _к — коэффициент теплообмена в процессе сушки Вт/(м 2 °С); t_n — температура поверхности материала, °C.

Коэффициент теплообмена « _к вычислялся по критериальному уравнению [6]

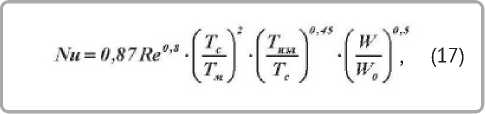
где Nu = a l / Х _воз — критерий Нуссельта; Х _воз - коэффициент теплопроводности воздуха; l — длина образца ткани по набеганию потока воздуха; Т_с , ^Т_ , Т_ж — абсолютные температуры среды, излучателя и мокрого термометра; критерий Рейнольдса Re = Wl / v _eo3 ; W — скорость воздуха, v _eo3 — коэффициент кинематической вязкости воздуха.

С другой стороны, тепловые потоки определялись по формуле излучения Стефана-Больцмана с поправкой на конвекцию [6, 7]:

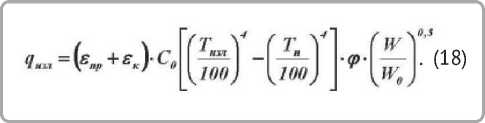
Угловой коэффициент излучения ф = 1.

Отношение (W / W) °- ⁵ поправка на уменьшение коэффициента теплообмена a _K и тепловых потоков q с уменьшением влагосодержания W .

Приведенная степень черноты системы находится из выражения

I                                   i

, где £1 и £2 — степени черноты поверхностей излучателя и ткани.

Участие конвективного теплообмена учитывается увеличением степени черноты системы за счет конвекции

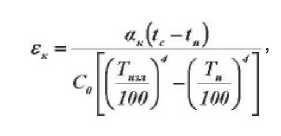
где а _к — коэффициент теплообмена, определяемый формулой (17), Вт/(м 2 °С); С ° — коэффициент излучения абсолютно черного тела, Вт/(м²К⁴).

Расчеты показали суммарное значение ( £ _пр + ^£ J ~ 0,59 — 0,62 для всех режимов сушки тканей. Несовпадение значений тепловых потоков, вычисленных по формулам (16) и (18), находятся в пределах точности проведения эксперимента.

На рисунке 6 дана зависимость тепловых потоков q от влагосодержания W и времени сушки т , полученная совместной обработкой эксперимента по уравнениям (16), (18) и кривых сушки тканей (рисунок 1). График, представленный на рисунке 6, может использоваться совместно с графиками на рисунке 3 и рисунке 5 при графическом расчете кинетики сушки тканей.

Плотность тепловых потоков находится по формуле

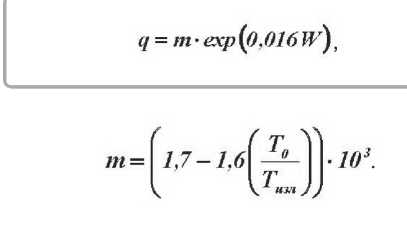
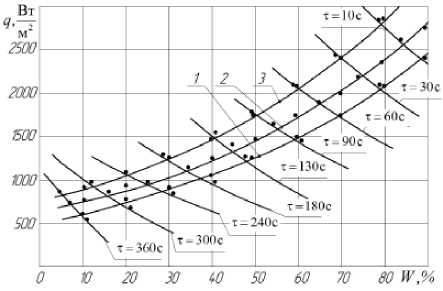
Рисунок 6 – Зависимость плотности теплового потока q от влагосодержания W и времени сушки τ для процесса сушки тканей при режимах, указанных на рисунке 2

ОЦЕНКА ТОЧНОСТИ ЭМПИРИЧЕСКИХ УРАВНЕНИЙ

На точность эмпирических уравнений, полученных на основе эксперимента, накладываются неизбежно ошибки, полученные при проведении и обработке эксперимента. Обработка экспериментальных данных проводилась наиболее точным методом, методом наименьших квадратов с минимальным разбросом опытных точек. Сопоставление результатов расчетных значений параметров, полученных по эмпирическим формулам, с экспериментом дано в таблицах.

В таблице 2 приведено сравнение расчетных значений времени сушки τ тканей из вискозы и льна с экспериментом, а в таблице 3 дано сопоставление расчетных значений среднеинтегральной температуры с экспериментом. Точность эмпирических уравнений находится в границах ошибки при проведении эксперимента. Обработку эксперимента в виде зависимостей, изображенных на рисунке 4, можно считать номограммой, поскольку при этом используются геометрические, внутренние и внешние характеристики теплопереноса, критерии подобия и обобщенные переменные.

кинетики сушки тканей и проводить расчеты графическим методом.

Установлены зависимости темпа нагревания влажного тела m_t и темпа убыли влагосодер-жания m_è от начального влагосодержания W₀ и основных параметров процесса сушки тканей. Использование метода регулярного режима дает возможность проводить расчет основных параметров кинетики сушки графическим методом по графикам, что позволяет значительно экономить время на проведение расчетной работы.

Результаты исследований и обработки экспериментальных данных в виде эмпирических уравнений и графиков, построенных на основе обобщенных переменных процесса сушки, могут использоваться в инженерной практике при расчетах конвективно-терморадиационной сушки тканей.

Метод регулярного теплового режима для описания кинетики процесса сушки может с успехом использоваться при различных способах подвода энергии материалу.

ВЫВОДЫ

Исследование процесса сушки тканей с комбинированным энергоподводом методом регулярного теплового режима позволяет, не прибегая к построению и интегрированию кривой скорости сушки, получить экспериментальные уравнения для расчета основных параметров

Таблица 2 – Сравнение расчетных значений времени сушки τ для тканей из вискозы и льна по уравнениям (5), (6), (12) и графикам рисунка 3 и рисунка 5 с экспериментом при разных режимах сушки

Вискоза. Режим сушки t_c = 80 ° C; Т_ию = 423 K

W, %	Тжс * ^	Т рас * (6)	Т ряс * (12)	Т рас * (5)	Т граф , с рис. 3	Тграф * с рис. 5
70	62	58	57	64	64	66
60	88	86	85	91	90	88
40	178	169	163	175	175	180
20	303	302	289	310	295	293
10	420	413	416	425	409	412
Вискоза. Режим сушки tc = 100 ° C; Тизё = 463 K
W, %	Т экс * с	Т рас * с (6)	Т рас , с (12)	Т рас ,с (5)	Т граф , с рис. 3	Тграф * с рис. 5
70	62	58	57	64	64	66
60	88	86	85	91	90	88
40	178	169	163	175	175	180
20	303	302	289	310	295	293
10	420	413	416	425	409	412
Вискоза. Режим сушки tc = 120 ° C; Тизё = 523 K
W, %	Т экс * с	Т рас * с (6)	Т рас , с (12)	Т рас ,с (5)	Т граф , с рис. 3	Тграф * с рис. 5
70	46	51	42	49	43	42
60	61	57	65	68	69	65
40	138	141	132	129	128	132
20	218	224	225	220	221	222
10	295	305	298	310	306	306
Лен. Режим сушки tc = 100 ° C; Tu3ji = 463 K
W, %	Т экс * с	Т рас * ^ (6)	Т рас , ^ (12)	Т рас ,^ (5)	Т граф * рис. 3	Тграф * рис. 5
80	45	43	43	41	42	43
60	62	64	65	59	62	59
40	95	95	96	89	93	87
20	149	154	155	145	150	146
10	198	205	207	189	191	189

Таблица 3 – Сравнение расчетных значений среднеинтегральной температуры t при сушке тканей из вискозы и льна по уравнениям (7), (10), (13), (15) и графикам рисунка 3 и рисунка 5 с экспериментом
Вискоза. Режим сушки tc = 80 ° C; Тизё = 423 K
W, %	т»с •мин	t 3KC , С	t pac . ° С (7)	t pac . ° С (10)	t pac . ° С (13)	t pac . ° С (15)	^ гpаф , ^ рис. 3	^ гpaф , ^ рис. 5
70	1,06	40	42	42	42	43	41	42
60	1,46	46	46	45	44	47	44	46
40	1,98	55	55	55	52	52	54	55
20	5,07	67	65	65	68	68	63	66
10	7	73	71	72	74	74	70	473
Вискоза. Режим сушки tc = 100 ° C; Т^ = 463 K
W, %	т»с •мин	t 3KC , С	рас , с (7)	t pac , С (10)	pac , с (13)	t pac , С (15)	гpaф , ^ рис. 3	гpaф , ^ рис. 5
70	0,77	46	42	42	47	44	44	44
60	1,31	53	50	50	52	54	49	51
40	2,57	66	62	6	61	68	62	3
20	4,41	76	72	72	73	78	73	77
10	6	80	77	78	83	82	82	85
Лён. Режим сушки t c = 100 ° C; Тизя = 463 K
W, %	т»с •мин	t^c , С	рарас , с (7)	t pac , ° С (10)	pac , с (13)	t pac • ° С (15)	гpaф , ^ рис. 3	гpaф , ^ рис. 5
80	0,76	47	45	46	43	—	44	45
60	1,1	51	48	51	49	—	49	55
40	1,5	54	52	55	54	—	58	62
20	2,5	62	61	67	62	—	69	70
10	3,3	67	68	73	66	—	76	78
Лён. Режим сушки tc = 120 ° C; Тизя = 523 K
W, %	т»с •мин	t экc , С	рас , (7)	t pac , С (10)	pac , (13)	t pac , С (15)	гpaф , ^ рис. 3	гpaф , ^ рис. 5
80	0,51	49	46	46	45	—	45	46
60	0,76	52	51	51	49	—	49	55
40	1,24	56	55	55	54	—	58	61
20	2	64	67	67	63	—	68	70
10	2,5	72	74	74	68	—	77	79