Графовая модель трехмерных упругих тел в декартовой системе координат

При численном решении разнообразных задач механики сплошной среды основными достаточно универсальными и широко распространенными являются методы конечных и граничных элементов в различных вариантах и сочетаниях с другими методами. Отличительная особенность этих методов состоит в том, что дискретизации подвергается не сама среда на этапе её моделирования, а уже созданная континуальная модель. Однако в ряде случаев использование дискретных подходов на более ранних этапах разработки и совершенствования моделей механики деформируемого твердого тела может привести к созданию новых эффективных численных схем и алгоритмов. Такие возможности открывает метод анализа полей деформаций и напряжений, использующий в качестве дискретных моделей сплошного тела ориентированные графы. Предлагаемый в работе подход основан на сочетании дискретных и энергетических представлений при моделировании процесса деформирования упругих сред. Дискретная модель при этом строится как первичная модель исследования, а способ перехода от континуума к системе с конечным числом степеней свободы основан прежде всего на физических соображениях. Основой для построения моделей в виде графов служит объективный характер операций измерения выбранных независимых переменных. Как известно, целью любого измерения является установление зависимости между значением переменной и показаниями прибора. В то же время измерение связано как с точками системы, между которыми оно осуществляется, так и с ориентацией измерителя. Эти свойства операции измерения можно представить направленным отрезком, т.е. дугой графа.

С точки зрения операции измерения все переменные вне зависимости от их физической природы могут быть подразделены на два типа – параллельные и последовательные [1, 2]. Параллельные переменные характерны тем, что измеритель подключается к двум точкам системы параллельно потоку энергии. Для измерения последовательных переменных прибор должен быть установлен в разрыв энергетического потока. К параллельным переменным относятся линейные и угловые разности перемещений, относительные скорости и ускорения, деформации, разности давлений, температур, электрических потенциалов и т.д. К последовательным переменным относятся силы, моменты сил, электрический ток, тепловой поток, поток жидкости или газа и другие. Выбор связной пары переменных определяется тем, что произведение последовательной и параллельной переменных должно давать скаляр с размерностью мощности или работы [2, 3].

Анализ системы на основе графового подхода сводится к тому, что 1) среда делится на части, имеющие известное математическое описание (в рассматриваемом ниже случае – закон Гука), 2) для каждой части строится подграф (элементарная ячейка), являющийся моделью этой части среды, 3) элементарные ячейки объединяются в граф – модель анализируемого тела, после чего с помощью матриц, характеризующих структуру графа, и уравнений, описывающих элементарные ячейки, получают уравнения системы в целом.

Вывод определяющей системы уравнений основан на использовании вершинного и контурного законов Кирхгофа [4]. Известно, что граф является моделью физической или технической системы только в том случае, если выбранные при его конструировании переменные удовлетворяют вершинному и контурному законам [2]. Эти законы были установлены Кирхгофом для электрических цепей применительно к токам и напряжениям. Впоследствии оказалось, что они носят фундаментальный характер и применимы ко всем последовательным и параллельным переменным, вне зависимости от их физической природы.

Согласно вершинному закону алгебраическая сумма последовательных переменных, инцидентных любой вершине графа, равна нулю, а в соответствии с контурным законом алгебраическая сумма параллельных переменных на любом замкнутом контуре равна нулю [4].

Дискретная модель деформируемого тела разрабатывалась под влиянием работ Г. Крона [5–8]. Крон, применяя аналоговое моделирование, предложил использовать электрические сети для представления самых разнообразных физических и технических систем. Он разработал эквивалентные электрические сети, предназначенные для моделирования задач гидродинамики, квантовой механики, теории упругости и пластичности, теории электрического и магнитного поля. Основное внимание в своих работах Крон обращал на универсальность возможностей при использовании уравнений, записанных в тензорной форме. Однако в работах не описан алгоритм конструирования эквивалентных электрических сетей и способы определения параметров элементарных ячеек. Подход Крона не получил распространения применительно к задачам механики сплошной среды. В работе [9] Е.Г. Кузовков обратил внимание на то, что при моделировании напряженно-деформированного состояния упругих тел можно обойтись без электромеханической аналогии, если эквивалентную электрическую сеть трактовать как ориентированный граф.

Способ конструирования графовой модели, ее конфигурация, применение специальным образом сконструированных матриц для вывода определяющей системы уравнений применительно к плоской и осесимметричной задачам теории упругости предложены Е.Г. Кузовковым и подробно изложены в [9–14]. В работе [11] на основе графовой модели построен двумерный сингулярный элемент для расчета напряженно-деформированного состояния в окрестности особых точек разреза. Использованию графового метода для анизо- тропных и неоднородных сред посвящены работы [16, 17]. Графовая модель упругой среды в полярной системе координат рассматривалась в [18]. В данной работе построена графовая модель упругой среды для решения пространственной задачи теории упругости.

1.    Конструирование элементарной ячейки

Способ конструирования графа тела связан с процессом измерения полного и независимого комплекта переменных, которые однозначно характеризуют деформированное состояние элементов, полученных в результате декомпозиции.

При построении графа исследуемого тела за исходные удобно взять те переменные, которые измеряются установкой прибора непосредственно на исследуемый объект, т.е. параллельные переменные.

Элементарной ячейкой будем называть подграф, соответствующий одному элементу, полученному при разбиении исходной области на мелкие части.

При определении конфигурации элементарной ячейки в прямоугольной декартовой системе координат область, занятую телом, покрываем сетью координатных плоскостей x = const, y = const, z = const, между узлами которых устанавливаем гипотетические измерители, определяющие абсолютные нормальные деформации δ хх , δ уу , δ zz и деформации δ ух , δ ху , δ zх , δ хz , δ zу , δ yz , обусловленные сдвигом. Рассмотрим шестигранный прямоугольный элемент со сторонами А х , A y, Az, расположенными вдоль осей ox, oy, oz соответственно. Комплект переменных, определяющих деформацию элемента, состоит из трех групп. Первая группа включает в себя δ хх , δ xу , δ xz , вторая – δ ух , δ уу , δ уz , третья – δ zх , δ zу , δ zz . В каждой группе одна переменная измеряется между парой точек, лежащих на определяющей оси группы, а две другие – между парой точек, находящихся на осях, перпендикулярных к определяющей. Так, например, δ хх измеряется между двумя точками оси ох , δ xу – между парой точек, лежащих на оси оу , а δ xz – между двумя точками оси oz . При этом δ хх представляет собой нормальную абсолютную деформацию, а δ ху , δ хz – относительные перемещения, вызванные поворотом грани со сторонами A y , A z . Измерители принимаем в качестве дуг графа, изображаем их направленными отрезками линий, причем ориентация дуг совпадает с ориентацией осей координат. Точки, между которыми проводим измерения, считаем вершинами графа. Здесь подразумевается, что используются идеализированные приборы, т.е. такие, что ножки нескольких из них могут быть одновременно установлены в одну и ту же точку тела. Поскольку одни и те же точки среды участвуют в разных группах измерений относительно осей х , у , z , то при построении графа они представляются разными вершинами. В результате получаем элементарную ячейку прямоугольного шестигранного элемента, имеющую 36 дуг и 24 вершины и состоящую из трех компонент (рис. 1).

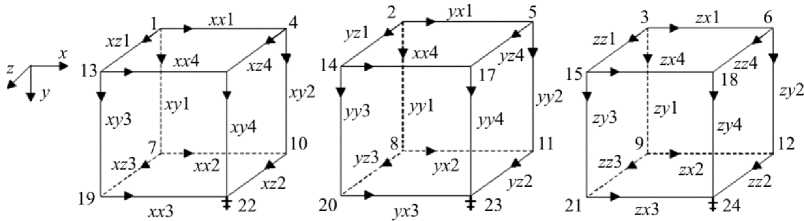
Рис. 1. Элементарная ячейка, состоящая из трех компонент Fig. 1. An elementary cell consisting of three components

Вершины с номерами 22, 23, 24 - корни подграфов соответствующих компонент элементарной ячейки. Каждая из дуг графа отображает одну из следующих пар параллельных и последовательных переменных: ( 5„ , f xx ), ( 5 _уу , f y ), ( 5 _zz , f zz ), ( 5 _ух , f ^ ), ( 5 _ху , f y \ ( 5 zx , ^f zx ), ^{( 5} xz , ^f xz ), ^{( 5} zy , f zy ),( 5 yz , ^f yz ), ^{где f} xx , ^f yy , f zz и f yx: , ^f xy , f zx , f xz , ^f zy , ^f yz нормальные и тангенциальные внутренние силы (обобщенные напряжения). Таким образом, дугам элементарной ячейки соответствует следующая пара векторов:

{ f } С = { f^x v.

¹ xx 4   z* yy 1        z* yy 4 z* yz 1 z* yz 4 1

, J ,..., J ,..., J ,..., Jl ^} ,

{6} С = {5 xx 1,..., 5 xx 4,5 yy 1,..., 5 yy 4,-, 5 yz      5 yz 4 } , где символ t обозначает операцию транспонирования, а индекс с указывает на принадлежность переменных отдельной элементарной ячейке.

2.    Матрица жесткости прямоугольного шестигранного элементас линейным полем деформаций

Связь элементарных векторов { f } c и { б } с , а также зависимость их от напряжений { о } и деформаций { а } упругого тела устанавливаем, принимая в качестве инварианта при переходе к дискретной модели энергию деформации произвольного элемента среды объемом V :

• IX ' И dv = { ^f } С { 8 } С •                                (2)

V где {б}c и {f}c определяются формулой (1). В результате энергию элемента в виде графа можно представить, с одной стороны, в виде

{f} С {8} c = f (Г 5 xx + f'^i + f"5zzi + f‘xi5 y* + fxyl5 xy + fzxi5zxi +

+ ("5 .+ fzyi5 .+ fyzi 5 xzi zyi yzi , с другой стороны, энергия деформации элемента сплошной среды есть

J {°}t {e} dv = J (°”axx + °yyаyy + °zzаzz + оxy Yxy + оxzYxz + оyzYyz) dv.             (3)

VV

Здесь напряжения связаны с деформациями законом Гука

°xx =(Х + 2ц)а xx +Ха yy +Ха zz,

°yy =^аxx +(^ + Mayy +^аzz , °zz =^аxx +^аyy +(^ + 2ц) аzz , °xy = ^Y xy, °xz = ^Y xz, °yz = ^Y yz

или в матричной форме

{ o }=№} ,

где

{o} t = {оxx, о yy, оzz, оxy, оxz, о yz } , {e} t ={e xx, E yy, E zz, Y xy, Y xz, Y yz}, а матрица упругости [Е] представима в блочном виде

[ ^Е ] =

E

n

Ε t

.

Матрицы [ Е n ] и [ Е t ] в (6) таковы:

	"X + 2 p	X	X "		p	0	0 "
[ Е . ] =	X	X + 2 p	X	, [ Е t ] =	0	p	0
	_ X	X	X + 2 p		_ 0	0	p_

,

где X , p - упругие постоянные Ламе.

При определении энергии деформации (3) требуется интегрирование выражения, содержащего неизвестные деформации и напряжения.

Для этого, учитывая дифференциальные зависимости Коши [19], аппроксимируем неизвестные деформации в пределах элемента следующими выражениями:

д u                                     д u , т ,

^E xx = — = a 0 ⁺ a l x ⁺ a 2 у ⁺ a 3 z , ^E yy =^ = ^Ь 0 ^{+ b} 1 x ^{+ Ь} 2 у ^{+ Ь} 3 z ,

дx                           дy

9 u,

E zz = -T- = c 0 + clx + c 2 y + c3 z, dz д U j j

—- = d 0 + d 1 x + d 2 y + d 3 z, дy д ux г , г , г , г — = f0 + f x + f2 y + f3 z , дz

^d u y

—- = e0 + e1 x + e2 y + e3 z, дx д u      .

— = g 0 ⁺ g 1 ^{x +} g 2 y ⁺ g 3 ^z , дx

^ ^Uy 7 7      7      7        6U

—- = h^ + hx + h₂y + hz , —- = i ₀ + ^x + z₂y + i₃z .

d z ^{01 2} 3 дy ^{0 1 2 3}

В результате соответствующую аппроксимацию получают du du         du du,        ди d ux

Y = —- + —-, Y = —- + —-, Y„ = —- + —-.

xy                       ^, yz                       ^, zx

дy дx        дz дy        дx дz

Заметим, что поскольку аппроксимируем деформации, а не перемещения, исключается ряд проблем, возникающих при смещениях элементов как твердого тела. Кроме того, значительно сокращается размер матриц, использующихся в расчетах.

В силу закона Гука (4) напряжения принимают вид

о xx =(X + 2p)( a 0 + a1 x + a 2 y + a 3 z) + X(b0 + b1 x + b2 y + b3 z ) + X( c0 + c1 x + c 2 y + c3 z),

о yy = X( a 0 + a1 x + a 2 y + a 3 z ) + X(b0 + b1 x + b2 y + b3 z ) + X( c 0 + c1 x + c 2 y + c3 z), о zz = Х( a 0 + a1 x + a 2 y + a 3 z) + X(b0 + b1 x + b2 y + b3 z ) + (X + 2ц) (c0 + c1 x + c 2 y + c3 z),   (8)

° xy = ЦУ xy =^[ = 0 ⁺ e о ⁺( = 1 ⁺ e i ) ^{x +} ( = 2 ⁺ e 2 ) У ⁺( = 3 ⁺ e 3 ) ^z ] , ° xz =цу xz =ц[ f 0 ⁺ g 0 ⁺( f ⁺ g 1 ) x ⁺ ( f 2 ⁺ g 2 ) У ⁺ ( f 3 ⁺ g 3 ) ^z ] ,

° yz = ЦУ yz = ц[ h 0 ⁺ e 0 ⁺( h i ⁺ e i ) x ⁺ ( h 2 ⁺ e 2 ) У + ( h 3 ⁺ e 3 ) ^z ] .

Рассматривая шестигранный элемент в форме прямоугольного параллелепипеда, поместим начало координат в центре элемента. Тогда в пределах элемента

■ A x	A x <  x < —,	-^ y <  y <^ y	-A z	A z < z < —
2	2	22	2	2

Выразим теперь неизвестные коэффициенты в (7) через деформации сторон шести-

гранного элемента. Как следует из (7)

A x 0 xx = f l u x dx = ( a 0 + a 2 y + a 3 z ) A x ,                            (9) - A x d x 2 A y 2 d u 0 xy = J " dy=y = ( d 0 + d 1 x + d 3 z ) A у ,                          (10) - A y 5 y 2 A z 0 xz = J ^u x dzz = ( f ) + f x + f 2 У ) A z .                          (11) - A z 5 z 2

комби-

Полагая в (9) поочередно y = ± -^y, z = ± ^z, получим при соответствующих нациях знаков

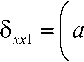
A У --a

A z    | a s I      A y

A z --a 2 ³

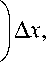
--a A x ,   0- = a +-- a,

₂ 3 xx 20 ₂ 2

⁰ xx 3 =1 a 0 ⁺ у a 2 ⁺ у ^a3 I A x , ⁰ xx 4 =

Ay    Az a 0 - у a 2 + у a 3

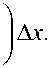
Из (12) находим, что

= ⁰ xx 1 ^{+ 0} xx 2 ^{+ 0} xx 3 ^{+ 0} xx 4     a = ⁰ xx 2 - ⁰ xx 1 ^{+ 0} xx 3 - ⁰ xx 4

0 ,+0 4-8 ,-0 з xx3 xx 4xx1xx2

2 A x A z

. (13)

4 A x        , ²          2 A x A y

Аналогично из (10),(11) получаем

5 ,+5 ,+8 ,+5 д 5 ,-8 ,+5 4-5 .     5 ,-5 ,+5 4-5 , xy1      xy 2xy3xy 4                xy 2xy1xy 4xy 3              xy 3xy1xy 4xy 2

=-------------------------, d i =-------------------------, d o =-------------------------

4 A y           ¹          2 A x A y         ³          2 A y A z

= ⁰ xz 1 ^{+ 0} xz 2 ^{+ 0} xz 3 ^{+ 0} xz 4     f = ⁰ xz 2 ^{+ 0} xz 4 - ⁰ xz 1 - ⁰ xz 3 f = ⁰ xz 2 ^{+ 0} xz 3 - ⁰ xz 1 - ⁰ xz 4

4 A z         , ⁷¹          2 A x A z       , ⁷²          2 A y A z       '

На основании контурного закона, алгебраическая сумма параллельных переменных на любом замкнутом контуре U x – компоненты элементарной ячейки равна нулю. На рис. 2 в качестве примера представлены четыре из шести контуров, образованных дугами этой компоненты при описании деформации сторон одной из граней элемента.

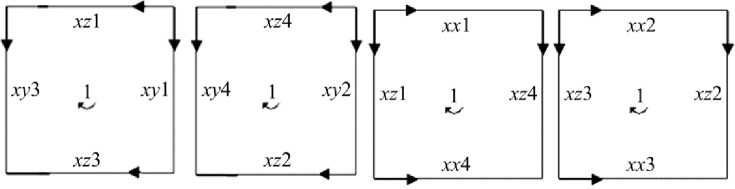
Рис. 2. Схема выбора контуров при записи уравнений Кирхгофа для параллельных переменных U x – компоненты ячейки 1 Fig. 2. Scheme of cycles for Kirchhoff’s equations for arcs variables of cell 1 ( U x Component)

Записывая все шесть соответствующих уравнений Кирхгофа, получим ^δ xx 1 ^+δ xy 2 ^-δ xx 2 ^-δ xy 1 ⁼ 0, ^δ xx 4 ^+δ xy 4 ^-δ xx 3 ^-δ xy 3 ⁼ 0, δ _{xx 1} +δ _{xz 4} -δ _{xx 4} -δ _{xz 1} = 0, δ _{xx 2} +δ _{xz 2} -δ _{xx 3} -δ _{xz 3} = 0, δ+δ-δ-δ= 0 δ+δ-δ-δ= 0 xz 1 xy 3 xz 3 xy 1^, xz 4 xy 4 xz 2 xy 2^, откуда

δxx1-δxx2=δxy1-δxy2,δxx4-δxx3=δxy3-δxy4,(15)

δxx1-δxx4=δxz1-δxz4, δxx2-δxx3=δxz3-δxz2,(16)

δ -δ =δ -δ δ -δ =δ -δ .(17)

xz 1 xz 3 xy 1 xy 3^, xz 4 xz 2 xy 2 xy 4

Складывая левые и правые части уравнений (15), а также (16) и (17), получим соответственно

δ xx 1	δ xx 2	+ δ xx 4	δ xx 3	δ xy 1	δ xy 2	+ δ xy 3	δ xy 4 ,
δ xx 1	- δ xx 4	+ δ xx 2	- δ xx 3	=δ xz 1	-δ xz 4	+ δ xz 3	δ xz 2 ,	(18)
δ xz 1	"5 ; xz 3	+ δ xz 4	- δ xz 2	=δ xy 1	- δ xy 3	+δ xy 2	- δ xy 4.

Равенства (18) с учетом (13), (14) дают a2= d1,a3=f1,f2=d3.(19)

Тот же результат следует из равенства смешанных частных производных: ∂ ² u_x   ∂ ² u _x ∂ ² u _x ∂ ² u _x ∂ ² u _x ∂ ² u _x

∂ x ∂ y ⁼ ∂ y ∂ x ^, ∂ x ∂ z ⁼ ∂ z ∂ x ^, ∂ z ∂ y ⁼ ∂ y ∂ z ^.

Интегрированием вдоль соответствующих сторон элемента выражений (7), связанных с u y , u z , аналогично предыдущему, найдем еще 18 коэффициентов:

5 । +5 ,+5 ,+5 4      5 ,+5 .— 5 .—5 , yy1 yy 2yy3yy 4               yy 2yy 4yy1yy 3

b = , b = , ⁰ 4 ∆ y ¹ 2 ∆ x ∆ y

,    ⁵ yy 3 ^{+ 5} yy 4 -5 yy 2 -5 yy 1          5 yx 1 +5 yx 2 +5 yx 3 +5 yx 4

b = , e_n =

• ³          2 Д y Д z          0           4 A x

e _ ⁵ yx 3 ^{+ 5} yx 2 - ⁵ yx 1 - ⁵ yx 4     e _ ⁵ yx 4 + ⁵ yx 3 - ⁵ yx 1 - ⁵ yx 1

• ²          2 Д x Д y       ,   ³           2 Д x Д z

h _ ⁵ yz 1 ^{+ 5} yz 2 ^{+ 5} yz 3 ^{+ 5} yz 4     h _ ⁵ yz 4 ⁺⁵ yz 2 - ⁵ yz 1 - ⁵ yz 3

0             4 Д z         ,    ¹           2 Д x Д z '

, _ ⁵ yz 3 ⁺⁵ yz 2 - ⁵ yz 1 - ⁵ yz 4         ⁵ zz 1 ⁺⁵ zz 2 ⁺⁵ zz 3 ⁺⁵ zz 4

h _ , c _ ,

• ²          2 Д y Д z         0           4 Д г

_ ⁵ zz 2 ^{+ 5} zz 4 - ⁵ zz 1 - ⁵ zz 3     _    ⁵ zz 2 ^{+ 5} zz 3 - ⁵ zz 1 - ⁵ zz 4

C _ , C _ ,

• ¹          2 A x Д z          ²          2 Д y A z

i _ ⁵ zy 1 ^{+ 5} zy 2 ^{+ 5} zy 3 ^{+ 5} zy 4     i _ ⁵ zy 2 ^{+ 5} zy 4 - ⁵ zy 1 - ⁵ zy 3

10”        4Дy        ,            2Дx Дy’

.     ⁵ zy 3 ⁺⁵ zy 4 - ⁵ zy 1 - ⁵ zy 2           ⁵ zx 1 ⁺⁵ zx 2 ⁺⁵ zx 3 ⁺⁵ zx 4

i3          2Дy Az       , g 0           4Ax,

5 ,+5 3-5     4       5 3+5, o   zx 2     zx 3     zx 4     zx 4      o   zx 3     zx 4     zx 1 zx 2

g ²”       2 Д x Д y      ^, g ³"       2 A x Д 2

Использование контурных законов для дуг Uy- и Uz-компонент позволяет получить равенства b1 e2, b3 h2, h1 e3, c1 g 3, c2 i3, i1 g 2 .

Подставляя напряжения (8) в уравнения равновесия:

daxx da xy da xz

----+----+----_0, dx    dyd dayy da xy dayz A dazz da xz dayz A

----+----+----_ 0, ----+----+----_0 dy    dx    dz        dz    dxd и пользуясь (19), (20), получим три уравнения относительно оставшихся пока не найденными коэффициентов a1, b2, c3, d2, e1, f3, g1, h3, i2:

( X + 2 ц ) a 1 + ц ( d 2 + f 3 ) _ — ( X + ц )( b 1 + C 1 ) ,

(X + 2ц)b2 + ц(e?1 + h3) _ — (X + ц)(a2 + c2),(22)

( X + 2 ц ) c ₃ +ц ( g 1 + i ₂ ) _— ( Х + ц )( a ₃ + b ₃ ) .

С целью их определения дополнительно предположим, что

( X + 2 ц ) a 1 _ ц ( d 2 + f3 ) ,	d 2 _ f 3 ,
( X + 2 ц ) b 2 _ ц ( e 1 + h 3 ) ,	e 1 _ h 3 ,                                (23)
( X + 2 ц ) c 3 _ ц ( g 1 + i 2 ) ,	g 1 _ i 2 .

Интерпретация этих условий состоит в следующем. Представление правой части в уравнениях (22) в виде суммы двух равных слагаемых позволяет произвести группировку коэффициентов, связанных с нормальными и тангенциальными составляющими тензора напряжений, после чего приравнять каждую группу к нулю. Кроме того, предполагая «равноправность» переменных введем условие на изменение компонент деформаций „                            ,              .                  ди сдвига. Так, например, условие d2 — f 3 из (23) означает, что--угол поворота к оси Ох ду линейного элемента, параллельного оси Оу, изменяется по переменной y точно так же,

„ „    ди,               _ _        _      „      _ _ как изменяется по z   x , т.е. угол поворота к оси Ох линейного элемента, параллельного

дz

_ „            д2 и д 2 ux дz2

оси Оz . В этом случае ^x д у 2

В результате найдем значения оставшихся коэффициентов:

a = K (b + c), f — d = Kb + c,)

1111  32211, b2 — K i ( a 2 + C 2 ) , ei — h — K 2 ( a 2 + c2 ) , c3 — K! (a 3 + b3), g! — i 2 — K 2 (a 3 + b3), где

X + pX+p

K —-, K — .

1    2 (X + 2p)     2

Кроме того, используя (19), (20) имеем d2 — f — K2 ( e2 + g3 ) , ei — h3 — K2 ( di + i3 ) , g 1 — i2 — K2 ( f + h2 ) .

С помощью найденных коэффициентов деформации внутри шестигранного элемента можно представить в виде

	H — [ L ] { 8 ) c ,		(24)
где
		F / 11    / 12    -    / 1,12                                1
		l 21    l 22    —    l 2,12                    °
[ L ] — F L n °	— 1	l 3!    l 32    —    l 3,!2	(25)
L ° L t J	2 A x A у A z	l 4,13    1 4,14    —    1 4,36
		0                   1 5,13    1 5,14    -    1 5,36
		_                               1 6,13     1 6,14     —    1 6,36 j

Элементы матрицы [ L n ] таковы:

/ 11 — 0,5 A у A z - у A z - z A у ,   l₁₂ — 0,5 A у A z + у N z - z A у ,

l13 — 0,5Aу Az + у Az + zAу,  l14 — 0,5 Aу Az - у Az + zAу,

/.. — /._ — - K.xAz ,   /_ — /.„ — K.xAz ,   L, — /... — - K. x A у ,

15 17           1             16 18        1             19 1,11           1

1 10 = 1 12 = K i x A У , 1 2i = 1 24 = - K i У A z , 1 22 = 1 23 = K i У A z ,

L. = 0, 5 A x A z - x A z - z A x , L- = 0, 5 A x A z + x A z - z A x , 25 ^{,                            ,} 26 ^{,                            ,}

1 27 = 0,5 A x A z - x A z + z A x , 1 28 = 0,5 A x A z + x A z + z A x ,

= Д 1 1 = - K У Ax , L. _n = L., = K, y A x , L = Lx = - K. z A y , 29 2,12          1            2,10 2,11       1            31 32          1

1 33 = 1 34 = K _i z A y , 1 ₃₅ = 1 36 = - K _i z A x , 1 ₃₇ = 1 38 = K _i z A x ,

1 39 = 0,5 A x A y - x A y - y A x , 1 3 _i0 = 0,5 A x A y + x A y + y A x ,

1 3 _n = 0,5 A x A y - x A y + y A x , 1 _3i2 = 0,5 A x A y + x A y - y A x .

Элементы матрицы [ L t ] имеют следующий вид:

1 ₄ ,i3 = 0,5 A y A z - ( i + K 2 ) y A z - z A y , 1 _4J4 = 0,5 A y A z + ( i + K 2 ) y A z - z A y ,

1 _{4 i5} = 0,5 A y A z + ( i + K 2 ) y A z + z A y , 1 _4i6 = 0,5 A y A z - ( i + K 2 ) y A z + z A y ,

1 _4i7 = 0,5 A x A z - ( i + K ₂ ) x A z - z A x , 1 _4i8 = 0,5 A x A z + ( i + K ₂ ) x A z - z A x ,

1 _4i9 = 0,5 A x A z - ( i + K ₂ ) x A z + z Ax, 1 _{4 20} = 0,5 A x A z + ( i + K ₂ ) x A z + z A x ,

14,2i   14,22     K2 У Ay,   14,23   14,24   K2 У AУ, l4,29

= 1 4 3o = - K ₂ x A x ,

¹ 4,3i     ¹ 4,32

= K ₂ x A x ,

¹ 5,i3    ¹ 5,i6      ^K 2 z ^{A z} ,    ¹ 5,i4    ¹ 5,i5    ^K 2 z ^A z ,

1 _{5 2i} = 0,5 A y A z - y A z - ( i + K ₂ ) z A y , 1 _{5 22} = 0, 5 A y A z + y A z - ( i + K ₂ ) z A y , 1 _{5 23} = 0,5 A y A z + y A z + ( i + K ₂ ) z A y , 1 _{5 24} = 0,5 A y A z - y A z + ( i + K ₂ ) z A y , 1 s 25 = 0,5 A x A y - ( i + K ₂ ) x A y - y A x , 1 _{5 26} = 0, 5 A x A y + ( i + K ₂ ) x A y + y A x ,

1 _{5 27} = 0, 5 A x A y - ( i + K ₂ ) x A y + y A x , 1 _{5 28} = 0, 5 A x A y + ( i + K ₂ ) x A y - y A x ,

l 5,33

= 1^ r = - KxAx,

5,36           2       ,

¹ 5,34     ¹ 5,35

= K ₂ x A x ,

¹ 6,i7 = ¹ 6,i9 =   ^K 2 z A z ,

l 6,18

¹ 6,20    ^K 2 z A z ,

¹ 6,25    ¹ 6,27      ^K 2 ^{У A У} ,    ¹ 6,26    ¹ 6,28    ^K 2 ^{У A У} ,

1 6 ₂₉ = 0, 5 A x A z - x A z - ( i + K ₂ ) z A x , 1 _{6 30} = 0,5 A x A z + x A z - ( i + K ₂ ) z A x , 1 _{6 3i} = 0,5 A x A z - x A z + ( i + K ₂ ) z A x , 1 _{6 32} = 0, 5 A x A z + x A z + ( i + K ₂ ) z A x , 1 6 33 = 0, 5 A x A y - x A y - ( i + K ₂ ) y A x , 1 _{6 34} = 0,5 A x A y + x A y + ( i + K ₂ ) y A x ,

1 ₆ 35 = 0, 5 A x A y - x A y + ( i + K ₂ ) y A x , 1 _{6 36} = 0, 5 A x A y + x A y - ( i + K ₂ ) y A x .

Подставляя { г } из (24) в (2), получим

f } С {б} c ЧИ t [L ]{б} cdv = J{°} t [L] dv {6} c . V                    V V 7

Отсюда после сокращения на { S } c и транспонирования имеем

{ f } c = [ [ L ] ‘ М dv .                                   (28)

V

Используя теперь закон Гука ( 5), получим

{ ^f } . = J [ ^L ]' [ ^E ][ ^L ] { ^S } c dv

V

Таким образом, уравнение элементарной ячейки приобретает следующий вид:

{ f } c = [ K ] c { S } c ,                                           (29)

где матрица жесткости элементарной ячейки [ K ] c определяется выражением

[ ^к ] . = ( [ L ]' [ E ][ L ] dv .

V

Поскольку матрица [L] из (25) транспонированная [L]1, а также матрица [E] из (6) блочные, то уравнение (29) можно представить в виде fK0δ nn n

\ f, J [ 0 K, Л S,, где связь между нормальными составляющими {fn}, {Sn} определяется матрицей

[ K , ] = J [ L , ]' [ E , ][ L , ] dv ,                                (30)

V а вторая часть между тангенциальными составляющими {f,}, {S t} - матрицей

[ K. ] = f [ L. ]' [ E t ][ L t ] dv .                                   (31)

V

Используя матричное умножение и последующее интегрирование, находим элементы матриц (30) и (31).

Матрица [ K n ] и [ K _t ] имеют следующую структуру:

			[[	[K"] [ K ,2	] [ K n 3 ]■
[ K . ]		=	[	K ] [ K 2 2	] [ K 23 ]	,
			_ [	[K n 2 ] [ K n2	■ [ k 2 3 ].
	1 K 11 ■ [	K	12	] [ K t 3 ]	0	)	0 ■
	[ K t 2 ] [	K t	22	]      0	0 [ k	25 ■	0
[ K t ] =	[ K t 3 ]	0		[ K 33 ]  [	K 34 ]	)	0 ,
	0	0		[ K 34 ]  [	K 44 ■     0		[ k 46 ■
	0     [	K t	25	]      0	0 [ k	55 ]	[ k 56 ■
	0	0		0     [	K 46 ] [ K	56 ]	[ k 66 ]_

Элементы матриц ^ K ^ ¹ J , ..., |^ K 66 J получены аналитически в явном виде, но здесь не приводятся из-за их громоздкости.

3.    Сходимость аппроксимации графового метода

Важно отметить, что континуальную модель сплошной среды удается полностью восстановить из ее дискретной модели в виде ориентированного графа. Покажем, что при уменьшении размеров сетки вершинный и контурный законы приводят к выполнению уравнений равновесия и совместности деформаций теории упругости, что влечет за собой сходимость приближенного решения к точному.

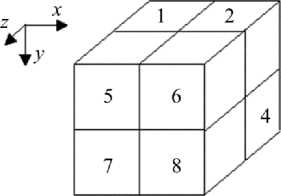
Рис. 3. Тело, состоящее из восьми элементов Fig. 3. A solid consisting of eight elements

Рассмотрим граф тела, состоящего из восьми элементов (рис. 3).

Он состоит из трех компонент U x , U y и U z . Для наглядности каждая компонента графа тела изображена на рис. 4 в виде двух частей. Компоненты U x , U y и U z для элементов верхнего слоя представлены на рис. 4, а , б , в , для элементов нижнего слоя – на рис. 4, г , д , е . Поэтому узлы нижней грани для первой составляющей части и верхней грани для второй составляющей части общие.

В соответствии с нумерацией центральная вершина графа тела получила для соответствующей компоненты номер 40, 41, 42 соответственно.

Согласно вершинному закону алгебраическая сумма последовательных переменных на каждой вершине графа равна нулю. Если дуга выходит из вершины, то силу, действующую на соответствующую точку элемента, принимаем положительной, если дуга входит в вершину – направление считаем отрицательным. В соответствии с этим для центральной вершины 40 Ux-компоненты получим xx 3xx3xx 2xx 2xz 2xz 2xz 3xz 3xx 4xx 4

• - f 1   + f 2   - ^f 5   + ^f 6   - ^f 1   + ^f 5   - ^f 2   + ^f 6   - ^f 3   + ^f 4 -

• xx1       xx1       xz 4xz 4xz1xz1xy1xy1xy 2xy 2

• - ^f 7   ^{+ f} 8   - ^f 3   ^{+ f} 7   - ^f 4   ^{+ f} 8   - ^f 6   ^{+ f} 8   - ^f 5  ^{+ f} 7   -            ⁽³²⁾

xy 3 xy 3 xy 4 xy 4

• - ^f 2   + ^f 4 - ^f 1 + ^f 3 = 0.

Здесь нижний индекс показывает номер ячейки, к которой относилась дуга.

Разложим значения внутренних сил элемента относительно их значений в смежных элементах в ряд Тейлора. Сохраняя два члена в разложении, получим f8

■ xx 3 ₊ a f l^{xx 3}

• 1   +

• - xx 1 ₊ d f xx ¹

• 7  +d

• • xy 1 , d f 6 xy ¹

• ■ xy 3 ₊ d f xy ³

2 +

Ax +—,

Ax +—,

Ay + ••■,

Ay + -,

xx 2

xx 2 xx 25

^f 6    = f 5 +

оx xx4

xx 4 xx 4 f 3

f 4   = ^f 3   + ~

оx xy2

fxx 2 _ fX^y 2 + ^fJ 5

7       5       dy xy4

xy 4 xy 4 f 1

Ax +—,

Ay + -,

Ay + -,

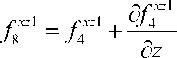
xz 3

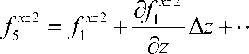
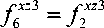
+ df2 dz

Nz +—,

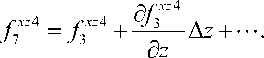
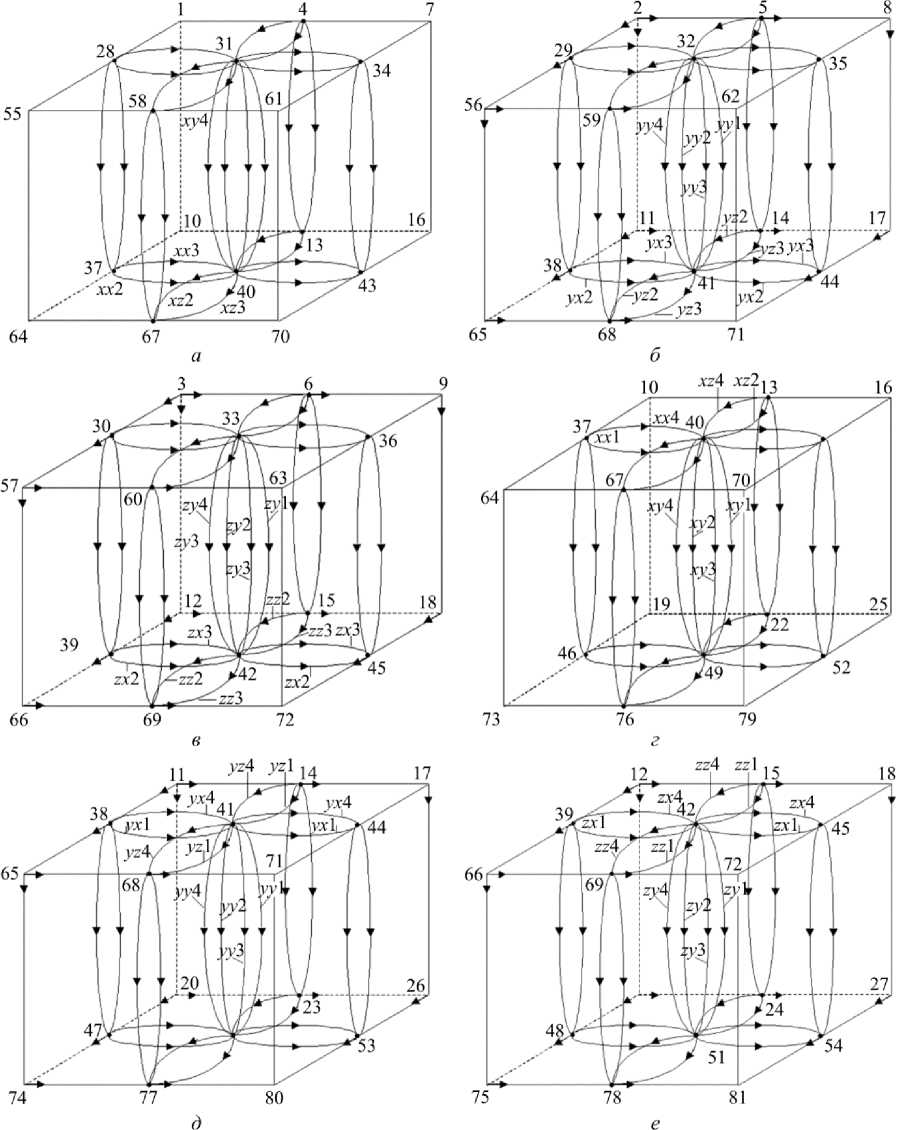
Рис. 4. Компоненты графа U x , U y , U z : ( а ), ( б ), ( в ) – для ячеек элементов 1 , 2 , 5 и 6 ;

( г ), ( д ), ( е ) – для ячеек элементов 3 , 4 , 7 и 8

Fig. 4. Components of a graph U x , U y , U z : а , б , в for cells 1 , 2 , 5 , 6 : г , д , е for cells 3 , 4 , 7 , 8

Подставляя (33) в (32), имеем xx1        xx 2xx3xx 4

^{д f} 7      ^{д f} 5      ^{д f}1       ^{д f}.

v дx    дx    дx

, ' д f 4 '^{z 1}

д x , , ^дJ1 -

Ax +

■f 6 xy ¹ , a f 5 -² + д f 2 xy ³ + a f ix-⁴ )

v S y д f x^{z 3}

д f 3" 4 )

д-    д- д- )

A- +

A z = 0.

v дz дz дz az v

Пользуясь теперь формулой (28) и матрицей (25) и выражая внутренние силы через напряжения, уравнение (34) после изменения порядка операций дифференцирования и интегрирования представим в виде

2 A x A - A z

J 1 Ax---^( 1ц + lj2 + li3 + lj4 ) ° + (l2i + 122 + 123 + 124 ) °— + (131 + 132 + 133 + 134 ) ° J +

V i   ax

^{+ A -} д Г ( ¹ 4,17 ^{+ 1} 4,18 ^{+ 1} 4,19 д- ^L

°+ ⁽ l ₅,i7 + 1 5,18 + l 5,19 + l 5,20 ) °  + ⁽ l 6,17 + l 6,18 + l 6,19 + 1 6,20 ) ° ^У ^| +

^{+A z} д _z ^{Г ( 1} 4,25 ^{+ 1} 4,26 ^{+ 1} 4,27 ^{+ 1} 4,28 ) ° ^ ⁺ ( ¹ 5,25 ^{+ 1} 5,26 ^{+ 1} 5,27 ^{+ 1} 5, ⁺ ( ¹ 6,25 ^{+ 1} 6,26 ^{+ 1} 6,27 ^{+ 1} 6,28 ) ° ^ ] } dv = ⁰¹

Подставляя в последнее равенство значения (26), (27), получим

° x" +

I

V v

д°xx   д°xy д°x")

11

дx    д-    дz )

dv = 0,

_{откуда при} произвольной области V следует первое уравнение из (21).

Точно так же уравнения вершинного закона для вершины 41 U y – компоненты и вершины 42 U z – компоненты

yz 3 yz 3 yz 4 yz 4 yz 1 yz 1 yx 3 yx 3

^f 2   ^{+ f} 6   - ^f 3   ^{+ f} 7   - ^f 4 ^{+ f} 8   - ^f 1    ^{+ f} - 2

yx 2 yx 2 yx 4 yx 4

' J 5 ^{+ f} 6    - ^f 3    ^{+ f} 4

f -x ¹ + f -x ¹ - J -- ⁴ + f -- ⁴ - f -- ³ + f -- ³

zx 3        zx 3

■^f 1    ^{+ f} 2

zx 2 zx 2 zx 4 zx 4

^f 5   ^{+ f} 6 - ^f 3   ^{+ f} 4

- J ^{-- 1} + J ^{-- 1} = 0, 68

zx 1        zx 1

^f 7 ^{+ f} 8

J 1 ^{zz 2} + J 5 ^{zz 2} - J z^{z 3} +

zz 3        zz 4 zz 4

⁺ J 6   - ^f 3   ^{+ f} 7

zz 1        zz 1        zy 4 zy 4 zy 2 zy 2

^f 4   ^{+ f} 8   - ^J 1   ^{+ f} 3   - ^f 5   ^{+ f} 7

-

J ,¹ + J 8 ^{z- 1}

-

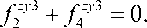
приводят к двум другим уравнениям равновесия (21).

Покажем теперь, что контурный закон приводит к уравнению совместности деформаций. Рассмотрим сначала контуры, образованные дугами ячеек 1 и 3 Ux – компоненты графа (рис. 5, а):

1111  3333

xx 1 xy 2 xx 2 xy 1^, xx 1 xy 2 xx 2 xy 1^.

Здесь и ниже верхний индекс показывает номер ячейки, к которой относится дуга. Поскольку

5 ¹ , =5 ³., xx 2 xx 1^,

из (35) получим

51 , +51 4-51 , +53 9 -53 9 -53, = 0.

xx 1 xy 2 xy 1 xy 2 xx 2 xy 1^.

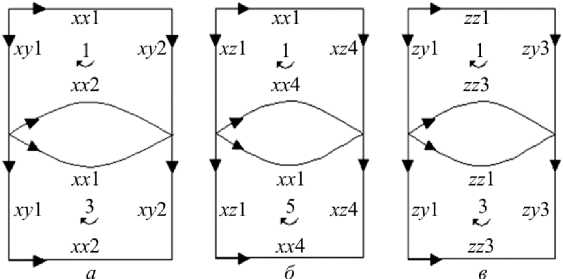
Рис. 5. Схема к записи контурных уравнений: а – для дуг U x – компоненты ячеек 1 и 3 ;

б – для дуг U x – компоненты ячеек 1 и 5; в – для дуг U z – компоненты ячеек 1 и 3

Fig. 5. Scheme of cycles for Kirchhoff’s equations: а – for arcs of cell 1 and 3 ( U x Component);

б – for arcs of cell 1 and 5 ( U x Component); в – for arcs of cell 1 and 3 ( U z Component).

Разложим деформации 5 xx 2 , 5³_xx 2 в ряд Тейлора, сохраняя в разложении по два члена:

5 ¹ -5 ¹ ₁+^{дS x, l} A y ;

xx 2 xx 1

дy

дб^ _А ⁵ xx 2 = ⁵ xx 1 + — xx ¹ A y .

оy

Отсюда, используя (36), получим

⁵ xx 2     ⁵ xx 1

д 5 1xx i

+ —-

55Li л I xx1 ay

дy    J дy

A y .

Следовательно, 5 xx 1 - 5 xx ₂

;   (55^ дX, )

^-5 xx 1 - ⁵ xx 1 ^- ^T x ^{1 +} ^f" ^A y ^A y .

(5y 9y J

Но s x, 1 - St 1 = $ x, 1 -5 xx 2 = -^ A y .

д y

Поэтому

s, ;            551я д2 5 . ) .

5xx 1 -5xx2 = - 2 X^ + ~~1 Ay Ay.

v дy    дy     J

Разлагая в ряд Тейлора деформации 5xy2,53xy 1,5xy2, получим e 1 _ e 1     d5 xy 1 a е X _ e1     d5 xy 1 д

5 xy 2 - 5 xy 1 + дx Ax, 5 xy1 = 5 xy1 + dy Лy ’ я («1 .d5xy 1д )

^{д 5} xy 1 ¹_r    ^A y

д5                     дy5L = 5Xи + —xy1 Ax - 5^ + ^----------J Ax.

xy ^{2      x} y ¹     д x           xy ¹              д x

Подставляя найденные отсюда выражения для 5 xy ₂ -5 xy 1 , 5 xy ₂ -5³ xy 1 , а также (X8)

в (37), получим f д51 , д 251 , 2xy1xy1

(  дx    дy дx

A y Ax J

^^^^^^^е

L д5 1 , д 2 5 ¹ , 2 — xx ¹ + xx ¹

(   д y    д y y

Ay Ay - 0.

J

8 u            8 u

Учитывая, что ovv ~  - Ax, о„, ~ - Ay, из (39) имеем xx                     xy

8x           оy d2 [ dux A d2 [ dux '' ^^^^^^^^^^^^^^^™ 1 ^^^^^^^^^^^^^^^^ I ^^^^^* ^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^™ 8y2 ( dx ) dx 8y ( dy v

= 0.

Рассматривая разность контуров, образованных дугами ячеек 1 и 2 Uy – компоненты графа (рис. 6, а), yx1 yx1 yy 2yy 2yx2yx 2yy1yy1, после аналогичных преобразований получим

8x 8y

[ 8 uy (5x )

d2 (du^' dx2 ( dy v

= 0.

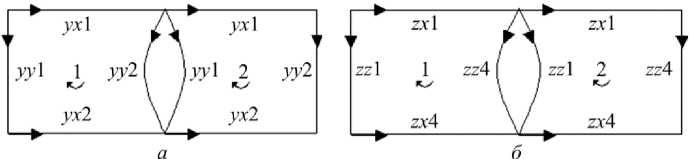
Рис. 6. Схема к записи контурных уравнений: а – для дуг U y – компоненты ячеек 1 и 2 ; б – для дуг U z – компоненты ячеек 1 и 2

Fig. 6 . Scheme of cycles for Kirchhoff’s equations: а – for arcs of cell

1 and 2 ( U y Component); б – for arcs of cell 1 and 2 ( U z Component)

Из уравнения (40) и (41), следует

d2 ( dux A d2 ----1 —x |+-- 8y2 ( 8x ) 8x2

^5 u_y

( 5y >

JL_ [^Hx.+^51) 8x 8y ( 8y 8x )

= 0

или первое из уравнений совместности деформаций в традиционной записи [19]

u G xx +yy = 1 xy

8 y ²     d x ²     d x d y

.

Совершенно аналогично получим:

• 1)    разности контуров ячеек 1 и 5 U x – компоненты (см. рис. 5, б )

5 1 ,-5 5, +5 1 .-5 5. -5 1 .+5 5. -5 1 ,+8 5, xx 1 xx 1 xz 4 xz 4 xx 4 xx 4 xz 1 xz 1

= 0

приводят к уравнению

d2£xx = 82  [ 8ux

8 z ²     8 x 8 z ( 8 z

• 2)    разности контуров ячеек 1 и 2 U z – компоненты (см. рис. 6, б )

zx 1 zx 1       zz 4 zz 4 zx 4 zx 4 zz 1 zz 1

= 0

к уравнению

92szz _ 92 f 9uz ^ "ax2" ”axsZ CaT J,

• 3)    разности контуров ячеек 1 и 3 U z – компоненты (рис. 5, в )

13131313 zz 1 zz 1 zy 3 zy 3 zz 3 zz 3 zy 1 zy 1

к уравнению

92szz _ 92 f 9uz'

9y2   9y9z (9y J,

• 4)    разности контуров ячеек 1 и 5 U y – компоненты (рис. 7, а )

11115555 yz 1 yy 3 yz 3 yy 1 yz 1 yy 3 yz 3 yy 1

к уравнению

92s yy _ a2 fSuy' 9z2    9y 9z ( 9z ,

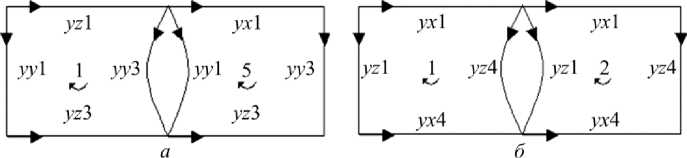
Рис. 7. Схема к записи контурных уравнений U y – компоненты: а – для ячеек 1 и 5 ;

б – для ячеек 1 и 2

Fig. 7. Scheme of cycles for Kirchhoff’s equations: а – for arcs of cell 1 and 5 ( U y Component);

б – for arcs of cell 1 and 2 ( U y Component).

Складывая уравнения (42) и (43), а также (44) и (45), получим еще два уравнения совместности деформаций

9^ 9 2s    92 yxz   9 2s   a s    92 у zz I xx xz zz ।         yy             y^"

9 x ²     9 z ²     9 x 9 z ,    9 y ²     9 z ²     9 y 9 z

Покажем, что выполняются также оставшиеся три уравнения совместности деформаций [19]. Рассмотрим , например, уравнение

9( »l yz, 3/ xz,»! xy Ъ,9 2s xx

11_ 2.

9x (   9x    9y    9z J    9y 9z

С учетом дифференциальных зависимостей Коши запишем его в виде

' 92 f5uy " ( 9x 9z Y9x ,

9x x

f9Uy )) f 99

^7”  ⁺ 7Т7Г

(9z J J (9x 9y

9 uz

9x

^^^^^^^^

^2-f9u^ 9x (9y

^^

+

J J

+

92 f9и ) 92 f9и )

x | x

9x 9y \(zz J 9x 9z (9 y ,

92 (9и^

9y 9z ( 9x

Используя контурный закон, покажем, что

8 д 8x дz ( дuy дx J д2 дx2 "д Uy ' v дz j = 0 (48) 81 дx дy Г 1 д н2 дx v д2 дx2 ^ди^ v Sy J - 0, (49) 82 дx дy ^д u x d дz 1-^^ J дx дz f дux x v дy J , (50) д2 дx дy f д u. x d дz 1= д2 J дy дz f д u v дx x i j . (51) Действительно, разность контуров ячеек 1 и 2 Uy компоненты (рис. 7, б) дает yx1 yx1 yz 4yz 4yx 4yx 4yz1yz1.

С помощью разложений в ряды Тейлора и равенства 8 ¹4 - 8²_z 1 получим

1              1                    1

• ⁸ yz 4 = ⁸ yz 1 + - ^A , дx

Z■ Z ж ⁸⁵ 2 z 1                d X1 ж ' z Л 1,

⁸ yz 4 = ⁸ yz 1 +     A x = ⁸ yz 4 +— 8 yz 1 +^— A x A x ,

Оx       d    оx ^      оxJ д81 .

1     1      yx121

yx 4     yx 1     dz      ’ yx 1     yx 1     dx z2    z-    '.■.        8S„              8S„1

• ⁸ yx 4 = ⁸ yx 1 +^— ^{A z} = ⁸ yx 1 +^— ^{A x} + — ⁸ yx 1 +^— ^{A x A z} .

оz            дx      оz d      oxJ

Пользуясь (53), из (52) получим

Ax Az--^yz! Ax2 = 0.(54)

dxdz

Так как d u„du„

8„* —y Ax, 8W« - Az,(55)

yx   dx        yzd то после подстановки (55) в (54) и сокращения на Ax2Az приходим к (48).

Точно так же уравнение (49) может быть получено из контурных законов, примененных к дугам ячеек 1 и 2 U z – компоненты, а уравнения (50) и (51) из тех же законов для контуров U x – компоненты ячейки 1 , изображенных на рис. 3. В результате из справедливости равенства (47) следует уравнение совместности деформаций (46).

Аналогично доказывается выполнение двух последних уравнений совместности деформаций

• 2____ yy _         ¹ yz + ¹ xy _— ° I xz

9x9z   9y ( 5 x    9z    9y )’

2 9 ²8 zz _ 5 Г 5y xz + 5y yz 5y xy 9x 9y  9z ( 9y    9x    9z _v

Таким образом, уравнения равновесия и совместности деформаций, входящие в традиционную постановку задач теории упругости, на графовой модели обеспечиваются автоматически, как следствие присущих графу фундаментальных зависимостей – вершинного и контурного законов. В связи с этим меняется роль уравнений равновесия и совместности деформаций – из основных соотношений при определении напряженно-деформированного состояния они превращаются во вспомогательный инструмент, позволяющий проконтролировать правильность построения графовой модели.

Выводы

• 1.    С помощью графового подхода построена матрица жесткости для восьмиузлового шестигранного упругого элемента с 24 степенями свободы при линейной аппроксимации деформаций. В методе конечных элементов (МКЭ) для такой аппроксимации требуется элемент, имеющий 20 узлов (60 степеней свободы) [20]. В результате определяющая система уравнений графового метода содержит уравнений примерно в 3 раза меньше по сравнению с системой, получаемой традиционным способом МКЭ.

• 2.    Показано, что фундаментальные законы теории графов (вершинный и контурный) обеспечивают выполнение условий равновесия и совместности деформаций для любого элемента, полученного при разбиении исходной области на мелкие части.